基于Petri网关联矩阵的流程模型间距离计算方法∗

吴亚锋　谭文安，2

（1.南京航空航天大学计算机科学与技术学院　南京　211106）（2.上海第二工业大学计算机与信息学院　上海　201209）

1　引言

在当今飞速发展的商业环境中，工作流技术得到工业界和学术界的广泛关注和深入研究，业务流程已经成为各类企业规范业务逻辑、高效处理业务流程的重要手段。通常为了保证企业的正常运作，不同企业部门的业务流程需要进行配合。同时，随着商业环境、客户需求和业务逻辑的不断变化，企业需要及时制定新的业务流程或改进原有业务流程来应对外界环境的变化。因此，一个大型集团企业大多会积累成百甚至数以千计的业务流程。为了高效管理积累下来的业务流程，各企业一般会建立自己的业务流程库。复杂的大规模业务流程库管理需要建立有效的流程索引和检索机制，而流程的索引和检索问题，首先要解决的就是流程间距离的计算问题，即业务流程的相似性问题。流程的相似性需求有着及其广泛的应用前景，例如：在业务流程整合过程中分析相似的业务流程，可以避免重复存储对整合效率的影响；在对流程库进行压缩时，可以选择相似流程类中的一个业务流程作为代表流程进行存储；不同组织部门的业务流程进行相似性分析，可以发现不同部门之间的合作关系，从而可以相互借鉴、相互学习；过程挖掘以及过程集成等许多业务过程管理的应用，都需要度量业务流程之间的相似性。

目前业务流程相似性度量一般基于三个方面：1）文本、节点标签；2）业务流程拓扑结构；3）业务流程行为轨迹。文本内容相似度的计算主要从节点的语法、语义、属性、类型和节点上下文进行计算［1～7］，这类方法计算简单、快捷，只需计算节点对应标签文本的相似度。然而，当流程结构发生改变影响流程间相似度时，该方法却无法捕获，因此准确性不是很高。流程结构相似度计算主要指流程拓扑结构的相似度。流程的拓扑结构主要体现了流程中的各个业务逻辑单元是通过何种逻辑关系连接起来的。现有的流程结构相似度［8～12］的研究大都是基于某种编辑距离来取得的，如图编辑距离、树编辑距离等。然而，流程结构相似度的计算仅考虑其静态拓扑结构并不能完全体现业务流程的具体行为和真实功能，无法响应动态改变的外部环境。关于流程行为相似度的计算，早期的方法主要集中于流程行为等价方面，如轨迹等价［13］、互模拟等价［14］等。然而，这些等价概念只能得到一个布尔值，即等价与非等价，不能精确地给出流程间的相似度值，因此，在大多数实际应用中是无效的。现有计算结果比较好的流程行为相似度计算方法有：因果足迹法［1］、紧邻变迁关系法［15］、行为轮廓法［16～17］和主变迁序列法［18］等。

本文方法参考文献［19］中使用的邻接矩阵来计算流程间距离，然而文献［19］的方法没有考虑不同控制节点的语义信息，因而无法区分不同控制节点间的差异。本文方法从流程模型的结构入手，首先给出带边权重的工作流网，然后使用带边权重的工作流网关联矩阵表示流程模型结构，通过计算对应带边权重的工作流网关联矩阵之间的距离来表示相应流程模型间的距离。

2　基础知识

首先介绍本文方法需要的一些基础知识，主要包括Petri网基本概念、工作流网概念，工作流网建模所用的基本组件以及Petri网的关联矩阵表示。

2.1　Petri网

Petri网是一种用于描述离散的、分布式系统的数学建模工具。它既能描述系统的结构，又能描述系统的运行。描述系统结构的部分称为网。从形式上看，一个网就是一个没有孤立节点的有向二分图。

定义1（Petri网）满足下列条件的三元组（P，T，F）称为Petri网：

1）P∪T≠ϕ

2）P∩T=ϕ

3）F⊆(P×T)∪(P×T)

4）dom(F)∪cod(F)=P∪T其中：P是库所的有限集合，T是变迁的有限集合，F是网的流关系。在建模过程中，一般使用库所代表条件，变迁代表事件。一个变迁有一定数量的输入和输出库所，分别代表可以使用的资源或者数据。

如图1所示的Petri网实例是由4个库所{p1，p2，p3，p4}和4个变迁{t1，t2，t3，t4}组成，由图1可知该Petri网中存在有分支结构，所以该Petri网有两种可能的运行轨迹，分别为：{p1，t1，p2，t2，p3，t4，p4} 和 {p1， t1， p2， t3， p3， t4， p4} 。

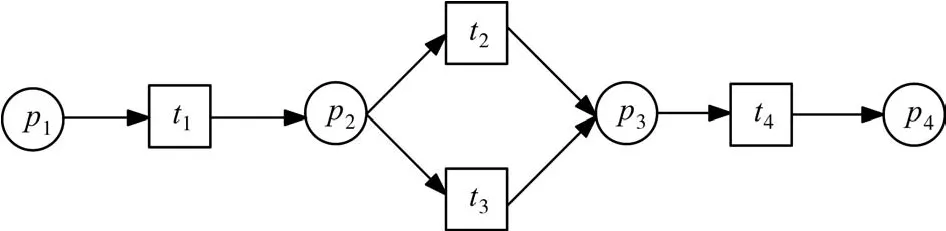
图1　一个Petri网实例

定义2（前集，后集）设 PN=(P，T，F)为一个Petri网，对于 x∈P∪T ，记

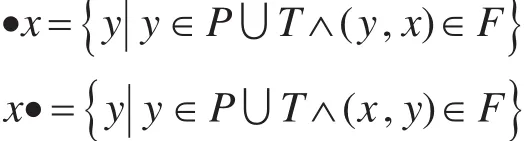
称·x为x的前集，x·为 x的后集。

2.2　工作流网

在Petri网的基础上，Aalst提出了工作流网的概念，工作流网是一种特殊的Petri网，其定义如下：

定义3（工作流网）一个Petri网 PN=(P，T，F)被称为工作流网，当且仅当其满足下面的条件：

1）PN有两个特殊的库所：i和o。库所i是一个起始库所，即·i=φ；库所o是一个终止库所，即o·=φ。

2）如果在PN中加入一个新的变迁t*，使t*连接库所 i和 o，即 ·t*={o}，t*·={i}，这时所得到的PN是强连通的。

从以上这两个对Petri网的约束条件不难看出：条件1）是使工作流网必须具有一个起始点和一个终止点；条件2）是使得工作流网中不存在处于孤立状态的活动和条件，所有的活动与条件都位于起始点到终止点的通路上。

在库所与变迁的基础上，为了定义出串行、并行、选择、循环等常见的过程逻辑，工作流网构造了一些结构化的组件来实现这些功能，在建模时用户可以直接使用这些组件，从而加快用户的建模过程。图2给出了工作流网的四类基本组件结构。

1）顺序组件。最简单的组件结构，活动按顺序一个接着一个地执行。

2）选择组件。两个或两个以上的活动存在选择关系且必须选择其中之一。选择组件开始于OR-split节点，最后汇合于OR-join节点。

3）并行组件。两个或两个以上的活动能按同时或以任意次序执行，且执行过程互不影响。并行组件开始于AND-split节点，最终汇聚于AND-join节点。

4）循环组件。某个活动需要被多次执行，直至满足跳出循环的条件。

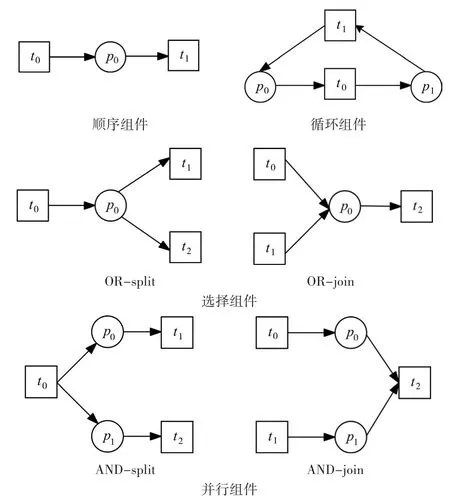
图2　工作流网基本组件

2.3　Petri网关联矩阵

Petri网的关联矩阵可以很好的描述一个Petri网的结构特征，下面给出Petri网关联矩阵的定义。

定义4（Petri网关联矩阵）设 PN=(P，T，F)为一个 Petri网，P={p1，p2，…，pm}，T={t1，t2，…，tn}，则Petri网 PN=(P，T，F)可以用一个n行m列的矩阵来表示A=(aij)n×m，其中：aij=aij+-aij-，i∈{1，2，…，n}，j∈{1，2，…，m}

3　流程间距离计算

本节首先给出节点边权重和带边权重工作流网的定义，然后介绍构造带边权重工作流网关联矩阵的规则，最后使用矩阵范数来定义流程间距离。

3.1　带边权重的工作流网

现有工作流的定义方式并不统一［20］，本文在文献［21～22］的基础上给出了带边权重的工作流的定义。首先我们定义节点边权重，然后给出带边权重的工作流。

定义5（节点边权重）任意给定一个工作流网，每个节点相邻的边上可以标记一个权重，该权重称为节点的边权重。

对工作流网的基本组件进行研究，我们可以发现以下一些规则：

并行组件结构都是由变迁引入或引出多条连接各个库所的结构，而且所有变迁中的事件都必将发生，只是发生的先后顺序不同。如图2中所示的AND-split和AND-join并行组件结构，我们可以给出如下规则：

规则1：任意给定一个合理的工作流网，对于其中任意的变迁节点，该节点所有的边权重都相等。

选择组件结构都是由库所引出或引入多条连接各个变迁的结构，多个选择分支只有一个能够发生，假设每个选择分支的发生可能性相等，则互斥分支发生的可能性是主干分支发生可能性的若干分之一，如图2所示的OR-split和OR-join选择组件结构，我们可以给出如下的规则：

规则2：任意给定一个合理的工作流网，对于其中任意的库所节点，该节点共有m条出边，出边权重分别为 w1，w2，…，wm，则有 w1=w2=…=wm。

工作流网可以看成一个流网络，我们可以使用图论中的相关结论对其进行研究。在一个流模型G=(V，E)中，其中V和E分别代表流模型的顶点集和边集，设s∈V和t∈V分别为流模型的源点和汇点，对于任意的边(u，v)∈E均有一非负容量c(u，v)≥0，可以在该流模型上定义流函数 f，该函数满足流守恒性，即对所有 u∈V{s，t}，要求f(u，v)=0。将该结论应用到工作流网中，则对于任意的非起始库所和非终止库所的出边的权重之和等于入边的权重之和。因此，我们可以给出如下规则：

规则3：任意给定一个合理的工作流网PN=(P，T，F)，i和o分别为其起始库所和终止库所，∀p∈P{i ， o}，库所 p的m条出边和n条入边的权重分别为 w1，w2，…，wm和θ2，…，θn，则满足=。

3.2　节点边权重的确定算法

对于一个合理的工作流网，按照一定顺序遍历工作流网中的所有节点，如果可以按照上述三个规则确定其边权重，则标记其权重，否则计算下一个节点，直到所有节点均被标记。

确定工作流网的边权重的算法如下：

算法1：确定工作流网的边权重。

1）首先添加两个库所Ps，Pe，两个变迁Ts，Te；

2）创建四条新边 (Ps，Ts)，(Ts，i)，(o，Te)，(Te，Pe)，同时将边 (Ps，Ts)和 (Te，Pe)的权重设置为1，其余边的权重设置为0；

3）创建一个队列Q，同时将队列初始化为Q={Ps}，所有节点设为未被访问过；

4）当队列不为空时，对于队列中的每一个节点x，如果x未被访问过，使用所给的三条规则计算节点x的边权重，并对该节点x进行广度优先搜索 BFS_Search(PN，x)；

5）当队列为空时，所有节点都被访问过，此时根据以上三个规则得到一个n元一次方程组，计算此方程组，将结果标记到PN的边上。

其中广度优先搜索节点x的步骤为

1）如果节点x可以根据上文规则求出边权重，则计算其边权重并标记，否则添加n个未知数x1，x2，…，xn，设为节点 x 的 n 条边的权重；

2）将该节点x标记为已访问过，并将其从队列Q中去除；

3）令AdjSet为与节点x紧邻且未被访问过的节点的集合；

4）对于AdjSet中的每个节点 y，将其添加到队列Q中，并递归地广度优先搜索该节点y。

定义6（带边权重的工作流网）任意给定一个合理的工作流网PN=(P，T，F)，如果所有节点的边权重都被标注完成，则称标注了边权重的工作流网为带边权重的工作流网，记为WPN。

图3为给图1所示的Petri网按照上面规则加上边权重后所得的带边权重的工作流网。

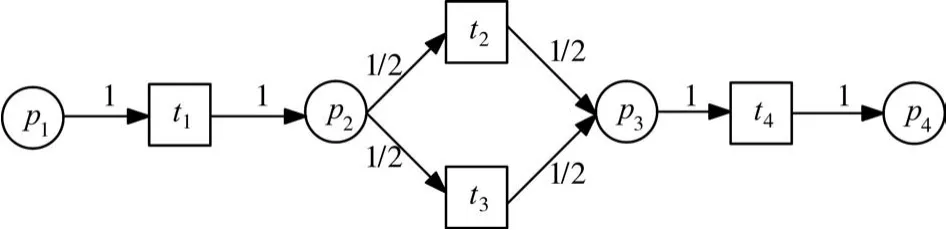
图3　带权重的工作流网

定义7（带边权重的Petri网关联矩阵）任意给定一个工作流网PN=(P，T，F)，对其每个节点的边加上权重后得到带边权重的工作流网，可以表示为WPN=(P，T，F，W)，其中W 为边权重集合，由WPN可以得到一个带边权重的Petri网关联矩阵WA=(waij)n×m，其 中 ：waij=wa+ij-wa-ij，i∈{1，2，…，n}，j∈{1，2，…，M。

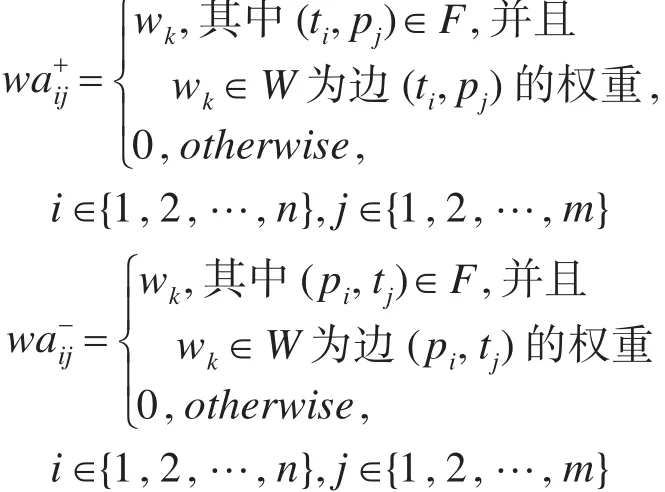
由于业务流程模型的数量、种类繁多，不同的业务流程模型对应不同的Petri网模型，它们的库所和变迁节点的个数往往是不同的，因此它们对应的关联矩阵的维数是不同的。在计算两个不同维数矩阵的距离时，我们需要对相应矩阵进行正规化处理，即将它们变为相同行与相同列的矩阵。下面给出Petri网关联矩阵正规化的定义。

定义8（Petri网关联矩阵正规化）给定两个工作流网 PN1=(P1，T1，F1)与 PN2=(P2，T2，F2)，它们所对应的带节点边权重的工作流网分别为WPN1=(P1，T1，F1，W1)和WPN2=(P2，T2，F2，W2)，其中W1和W2分别表示节点的边权重集合，正规化带边权重的Petri网关联矩阵的行数为N= | T1∪T2|，列数为M= | P1∪ P2|，T1∪ T2={t1，t2，…，tN} ，P1∪ P2={p1，p2，…，pM}，由WPN1和WPN2可以得到两个正规化带边权重的Petri网关联矩阵NWA1=(N×M和NWA2=N×M，其 中 ：=--n，i∈{1，2，…，N}，j∈{1，2，…，M}。

由以上分析可知，任意给定两个Petri网模型PN1和 PN2，通过算法1给Petri网增加节点边权重，可以得到带边权重的Petri网模型WPN1和WPN2，若所得的WPN1和WPN2维数不同，则需要对Petri网关联矩阵进行正规化处理，得到两个正规化带边权重的Petri网关联矩阵NWA1=(nwa1ij)N×M和 NWA2=(nwa2ij)N×M，本文认为 NWA1和NWA2可以很好地表示Petri网模型PN1和PN2的结构特性。因此，可以通过计算NWA1和NWA2之间的距离来反映Petri网模型PN1和PN2之间的距离。

3.3　流程间距离计算

流程间距离的计算可以分为定性分析与定量计算，所谓定性分析是指对流程模型的规模大小进行比对，如果两个流程模型的规模不相同，则它们之间一定存在距离，反之不然。对流程模型的定性分析是对流程模型距离定量度量的基础和准备，通过简单的定性分析，确定那些一定存在距离的流程模型；而定量计算则指在确定流程模型之间存在距离之后，就需要计算出流程模型间距离的具体数值。由于本文是使用Petri网关联矩阵来表示业务流程模型的结构特征。所以两个流程模型间的距离可以通过计算两个关联矩阵的距离来表示。在矩阵论中，矩阵间距离的度量可以使用范数，因此，本文给出如下的流程模型间距离的定义。

定义9（流程间距离）任意给定两个Petri网模型PN1和PN2，可以得到两个正规化带边权重的Petri网关联矩阵NWA1=(nwa1ij)N×M和NWA2=(nwa2ij)N×M，模型 PN1和 PN2之间的距离定义为：d(PN1，PN2)=tr[(NWA1-NWA2)×(NWA1-NWA2)Τ]，其中tr[]表示矩阵的迹，即矩阵主对角线上元素之和。

定理1对于任意给定的Petri网模型PN1，PN2和PN3，模型间距离满足距离度量特性，即：

1）非负性：d(PN1，PN2)≥0 ，当且仅当 PN1=PN2成立时，有 d(PN1，PN2)=0 ；

2）对称性：d(PN1，PN2)=d(PN2，PN1)；

3）三角 不 等 式：d(PN1，PN3)≤d(PN1，PN2)+d(PN2，PN3)。

证明：1）由流程间距离的定义可知d(PN1，PN2)≥0 ，若 d(PN1，PN2)=0 ，则说明 NWA1-NWA2是零矩阵，从而得 NWA1=NWA2，即 PN1=PN2，反之亦然；

2）由流程模型间距离的定义可得：

4　实验验证

首先使用人工创建的5个实例模型将本文方法与文献［19］所给方法进行对比，以证明本文方法的可行性与有效性。然后使用IBM所提供的真实数据集，对本文所提方法的性能进行分析。实验环境为：Inter（R）Core（TM）i5-6420P CPU@2.80GHz 8GB内存。实验程序使用Java语言编写，运行在64位W indows7系统上，JDK版本为1.7.0。

4.1　实例分析

本文定义的流程模型间距离与文献［19］所给的流程模型间距离定义类似，因此以文献［19］的方法作为对比实验来证明本文方法的可行性与有效性。将文献［19］的方法称为流程依赖图（Process Dependency Graph，PDG）算法。如图4描述了5个典型的工作流模型，其中WF1是一个简单的顺序工作流，其他4个工作流网都是在其基础上通过简单的增加、删除和替换节点的操作得到，目的是保证实例中的结构类型足够多样，覆盖所有4种基本组件结构以及基本组件的组合，以证明结论的有效性。

通过对图4所示的5个工作流模型使用PDG算法，得到的工作流模型间距离如表1所示，其中工作流模型WF2，WF3，WF4都是在顺序组件上改造后形成的带有选择、并行和循环等基本组件的流程模型，他们与WF1的距离都相同，说明PDG算法在对顺序结构进行基本组件结构改造后无法有效区分进行了哪种修改；WF2与WF4之间的距离为0，说明这两个工作流是完全相同，而通过人工观察发现WF2和WF4的基本组件不同，说明WF2和WF4的流程模型间距离应该大于0，可以发现PDG算法无法有效区分选择组件结构和并行组件结构，即不能对流程运行的互斥和并行关系进行有效的识别。

表1　PDG算法得出的流程间的距离

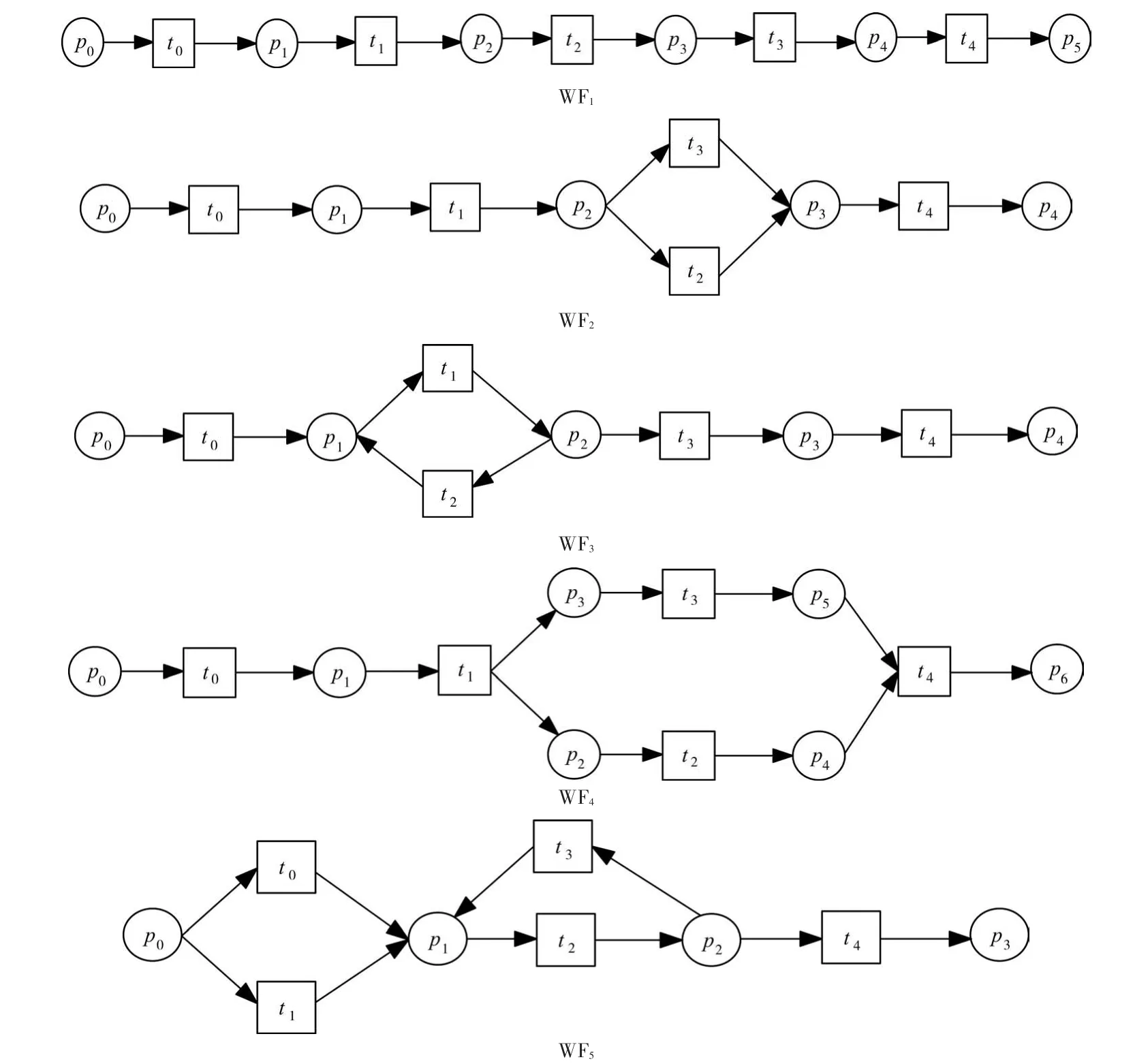
图4　人工流程模型实例

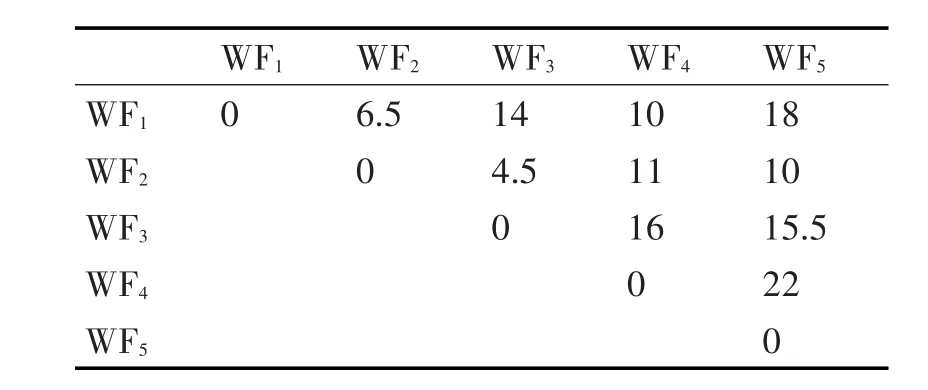
表2　通过本文方法求得的流程间距离

表2是通过本文所给方法得出的流程模型间距离。通过表2可以发现，在对顺序组件进行选择、并行和循环改造后所得流程模型与原流程模型间的距离是不相同的，因而可以判定所进行的是不同的改造；WF2和WF4之间的距离大于0，因而可以有效地判定WF2和WF4是不同的流程模型结构，即本文方法可以对选择组件结构和并行组件结构进行有效区分。

4.2　性能评估

实验数据使用IBM公开的一组数据集［23］，包括5个流程库，总共3000多个流程，这些流程是在对客户项目进行建模后获得的。其涉及多个领域，如保险、供应链、银行、建筑、自动化、通信等。在这些流程中隐去了原来的详细信息，如重命名流程库名为A，B1，B2，B3，C，变迁名由T1，T2，T3，…来代替，库所名由P1，P2，P3，…来代替。匿名后的流程忽略了原先的实际含义而只考虑其流程模型的结构信息。表3展示了它们各自的库所、变迁、边数的最小值、最大值和平均值等信息。

表3　数据集

从每个流程库中分别挑选出五个流程模型，挑选出的流程模型分别为：包含5个库所和5个变迁、10个库所和10个变迁、15个库所和15个变迁、20个库所和20个变迁，以及25个库所和25个变迁的流程模型。将挑选出的25个流程模型分成5组，每组中流程模型的库所和变迁个数相等。从而每组内的流程模型可以形成10对。可以求出计算流程模型间距离所花的时间，如图5（a）所示，以及每组所花时间的平均值，如图5（b）所示。

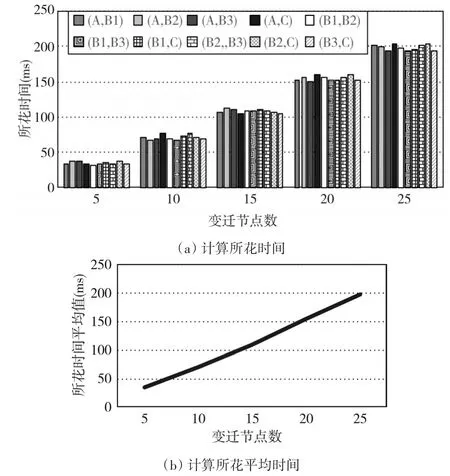
图5　

由图5（a）可知，随着流程模型规模的增大，计算流程模型间距离所花的时间也相应增加。由图5（b）可知，计算流程模型间距离所花时间的平均值与流程模型中变迁节点数呈现多项式关系。这与算法1的时间复杂度是一致的。算法1进行了一次广度优先搜索，在遍历过程中仅做了变量标记，算法的遍历操作的时间复杂度为O（V+E）。该时间复杂度是多项式的，即对于任意给定的工作流网，理论上都可以在多项式时间内确定其边权重。

5　结语

业务流程管理对于企业提高工作效率，改善工作质量，实现流程优化至关重要。如何计算流程模型间距离，从而实现流程索引与检索技术是企业必须解决的关键问题。本文对现有的工作流相似性度量工作进行分析研究，以Petri网为建模基础，在工作流网的基础上定义了带边权重的工作流网，利用Petri网关联矩阵表示流程模型的结构特征，借鉴矩阵范数给出了流程间距离的定义，并且给出了流程模型间距离的计算过程。定义的流程模型间距离满足距离度量的三个特性。

在未来工作中，需要寻找更加高效的边权重确定算法，从而加快流程模型间距离的计算。将本文方法应用到流程索引与检索领域，实现业务流程的快速查找。

［1］Dijkman R，Dumas M，Dongen B V，et al.Similarity of business processmodels：Metrics and evaluation［J］.Information Systems，2011，36（2）：498-516.

［2］Akkiraju R，Ivan A.Discovering Business Process Similarities：An Empirical Study with SAP Best Practice Business Processes［C］//Service-Oriented Computing-，International Conference，ICSOC 2010，San Francisco，Ca，Usa，December7-10，2010.Proceedings.2010：515-526.

［3］Yan Z，Dijkman R，Grefen P.Fast Business Process Similarity Search with Feature-Based Similarity Estimation［C］//On the Move to Meaningful Internet Systems：OTM 2010.Springer Berlin Heidelberg，2010：60-77.

［4］Minor M，Tartakovski A，Bergmann R.Representation andStructure-BasedSimilarity Assessment for Agile Workflows［C］//International Conference on Case-Based Reasoning：Case-Based Reasoning Research and Development.Springer-Verlag，2007：224-238.

［5］Huang K，Zhou Z，Han Y，etal.An Algorithm for Calculating Process Similarity to Cluster Open-Source Process Designs［J］.2004，3252：107-114.

［6］Levenshtein V I.Binary codes capable of correcting deletions，insertions and reversals［J］.Problems of Information Transmission，1965，1（1）：707-710.

［7］Miller G A.WordNet：a lexical database for English［J］.Communicationsof the Acm，1995，38（11）：39-41.

［8］Dijkman R，Dumas M，Garc&#，et al.Graph Matching Algorithms for Business Process Model Similarity Search［C］//Business Process Management，International Conference，Bpm 2009，Ulm，Germany，September 8-10，2009.Proceedings.2009：835-842.

［9］Grigori D，Corrales JC，Bouzeghoub M，et al.Ranking BPEL Processes for Service Discovery［J］.IEEE Transactionson Services Computing，2010，3（3）：178-192.

［10］Rosa ML，Dumas M，Uba R，et al.Merging Business ProcessModels［C］//On the Move to Meaningful Internet Systems：OTM 2010.Springer Berlin Heidelberg，2010：96-113.

［11］Li C，ReichertM，Wombacher A.On Measuring Process Model Similarity Based on High-Level Change Operations.［C］//Conceptual Modeling-ER 2008，International Conference onConceptual Modeling，Barcelona，Spain， October 20-24， 2008.Proceedings.2008：248-264.

［12］Kunze M，Weske M.M.：Metric Trees for Efficient Similarity Search in Large Process Model Repositories［J］.Lecture Notes in Business Information Processing，2011，66：535-546.

［13］Pomello L，Rozenberg G，Simone C.A survey of equivalence notions for netbased systems［C］//Advances in Petri Nets 1992.Springer BerlinHeidelberg，1992：410-472.

［14］Glabbeek R JV，Weijland W P.Branching Time and Abstraction in Bisimulation Semantics（Extended Abstract）.［J］.Journalof the Acm，1991，43（3）：555-600.

［15］Zha H，Wang J，Wen L，etal.A workflow net similarity measure based on transition adjacency relations［J］.Computers in Industry，2010，61（5）：463-471.

［16］Weidlich M，Mendling J，Weske M.Efficient Consistency Measurement Based On Behavioural Profiles of Process Models［J］.Software Engineering IEEE Transactionson，2011，37（3）：410-429.

［17］Weidlich M，Polyvyanyy A，Mendling J，etal.Efficient Computation of Causal Behavioural Profiles Using Structural Decomposition［C］//Applications and Theory of PetriNets.Springer Berlin Heidelberg，2010：77-685.

［18］Wang J，He T，Wen L，et al.A Behavioral Similarity Measure between Labeled Petri Nets Based on Principal Transition Sequences［C］//On the Move to Meaningful Internet Systems：OTM 2010.Springer Berlin Heidelberg，2010：394-401.

［19］Bae J，Liu L，Caverlee J，etal.Developmentof Distance Measures for Process Mining，Discovery and Integration［J］.International Journal of Web Services Research，2007，4（4）：1-17.

［20］Guo X，Sun S X，Vogel D.A Dataflow Perspective for Business Process Integration［J］.Acm Transactions on Management Information Systems，2015，5（4）：1-33.

［21］Alonso G，Mohan C，Agrawal D，et al.Functionality and Limitations of Current Workflow Management Systems［C］//1997：754-763.

［22］Mohan C.Recent Trends in Workflow Management Products，Standards and Research［C］//Workflow Management Systems and Interoperability.Springer Berlin Heidelberg，1998.

［23］ Fahland D，Favre，C&#，dric，et al.Instantaneous Soundness Checking of Industrial Business Process Models［C］//International Conference on Business Process Management.Springer-Verlag，2009：278-293.