紊流强度与积分尺度对结构平均风压与脉动风压雷诺数效应影响研究

白　桦， 郭聪敏， 刘健新

(长安大学 公路学院公路大型结构安全教育部工程中心， 陕西 西安 710064)

0　引言

建筑结构位于大气边界层风场中，随着建筑高度增大，对风的敏感性会逐渐增强.目前高耸与大跨屋盖结构抗风性能研究主要依赖风洞试验.受模型尺寸和试验风速限制，风洞试验时的雷诺数量级与实际结构雷诺数量级存在明显差异，可能会导致某些气动响应测量误差.李加武研究了极端桥梁断面雷诺数效应，指出传统低雷诺数风洞试验得出的测力试验结果偏保守[1].为了弄清楚雷诺数效应会给土木结构风洞试验结果带来哪些影响，国内外学者进行了大量研究.Barre以诺曼底桥为研究对象，制作了三种不同缩尺比模型，研究雷诺数效应的影响，得到的三分力系数曲线不一致，特别是升力系数曲线,这表明升力系数对雷诺数较敏感[2].金挺通过试验发现扁平流线形断面雷诺数效应比较突出，随雷诺数变化，三分力系数变化幅度约为50%[3].Schewe通过钝体断面尾流形状研究雷诺数效应，认为雷诺数效应同样会使钝体断面产生30%左右的变化幅度[4].Tieleman研究了紊流风特性参数对钝体结构表面风荷载的影响，结果表明，只要模型的特征尺寸大于2倍紊流积分尺度，则积分尺度的影响会很小，但紊流强度反映了小尺度紊流的作用，对模型负压区结果的影响非常明显，需要严格模拟[5].Edward 通过研究紊流控制方法抑制试验时的雷诺数效应[6].Matsubara研究指出，在低雷诺数(Re≤4 000)情况下，也会产生大尺度的波动，从而影响结构表面压力分布[7].李加武等人通过大比例尺节段模型试验，研究了较大雷诺数量级的流线形断面与钝体断面三分力系数，指出雷诺数效应对流线形桥梁断面影响较钝体断面大，紊流或增大模型表面粗糙度可以有效抑制雷诺数效应，特别是阻力系数[8-9].华旭刚对输电塔进行了研究，发现紊流积分尺度会使风振系数结果偏保守，并给出了紊流积分尺度修正系数[10].卢占斌采用不同紊流参数的局部紊流场对CAARC模型进行试验，发现紊流强度与积分尺度均会对风洞试验结果产生影响[11].

虽然风洞试验时的雷诺数量级偏小很多，但可以通过大量的比对试验，尝试找到雷诺数效应的影响规律.前述学者的研究结果表明，风洞试验时，雷诺数效应可能会对试验结果产生影响.产生雷诺数效应的根本原因可能是风特性参数的变化导致结构表面风压分布规律发生变化.为了研究这些影响，笔者制作了两个不同缩尺比模型，在风洞中采用格栅模拟了16种不同的局部紊流风场，分别形成了紊流强度相同但积分尺度不同和积分尺度相同但紊流强度不同的几种风场，以此来研究矩形结构雷诺数效应，以及紊流强度与积分尺度对矩形结构雷诺数效应的影响.

1　风洞试验

1.1　试验流场

试验设计如图1和表1、表2所示.

图1　格栅风场Fig.1　Turbulence field of grilles

%

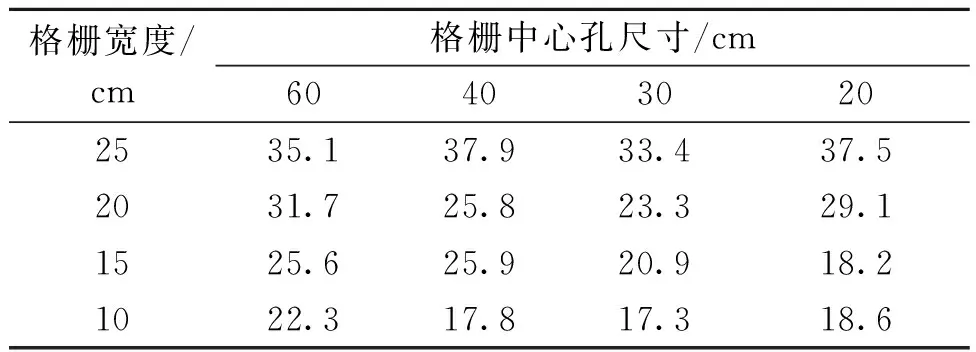
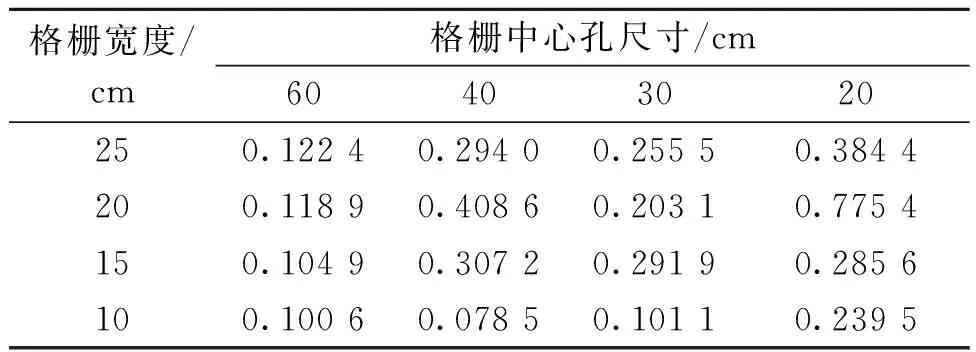
表2　各工况紊流积分尺度Tab.2　The turbulence integral scale of different schemes　m

1.2　试验模型

制作两种尺度模型，最小尺度模型为横截面尺寸为10 cm的正方形，高30 cm.大尺度模型是小尺度模型的2倍，外形相同，等比例放大.风速相同时，大尺度模型雷诺数是小尺度模型的2倍，模型分区示意如图2所示.图3为各分区测点布置图，两种尺度模型测点的相对位置保持一致.试验照片如图4所示.为保证数据稳定性，试验风速选择8 m/s与10 m/s两种，每个风速下采集3组数据，将6组数据取平均.试验装置选择美国PSI公司电子压力扫描阀，采样频率312.5 Hz，采样时长60 s.

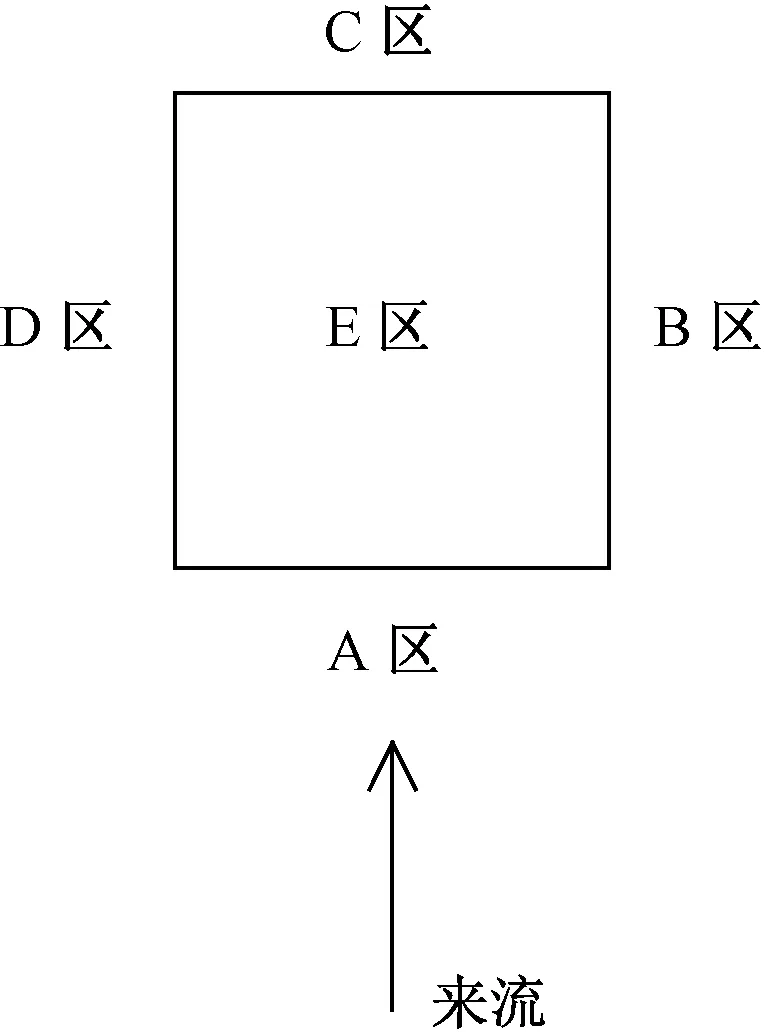
图2　模型分区示意Fig.2　Model partition

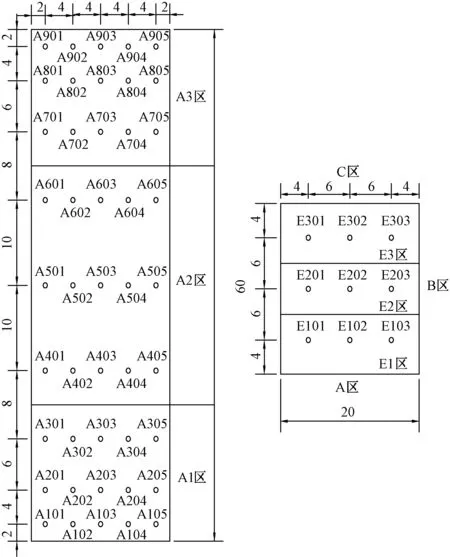
图3　模型测点Fig.3　Measuring point arrangement

图4　模型试验照片Fig.4　Photos of model test

1.3　数据处理

各测点无量纲压力系数可按式(1)计算，

(1)

式中：Cpi为测点i处的压力系数；Pi为作用在测点i处的压力；P0和P∞分别是试验时参考高度处的总压和静压.本试验参考点高度取模型顶部位置.由风压系数时程可分别得到平均风压和脉动风压.

2　试验结果及分析

2.1　风场不变时平均风压雷诺数效应

由于矩形结构表面极值风压通常出现在迎风面及背风面中部区域，限于篇幅，笔者主要分析模型第5行与第3列风压雷诺数效应.图5为第5行与第3列测点位置示意图.图6为在格栅10～20风场中第5行与第3列平均风压系数随雷诺数变化情况.

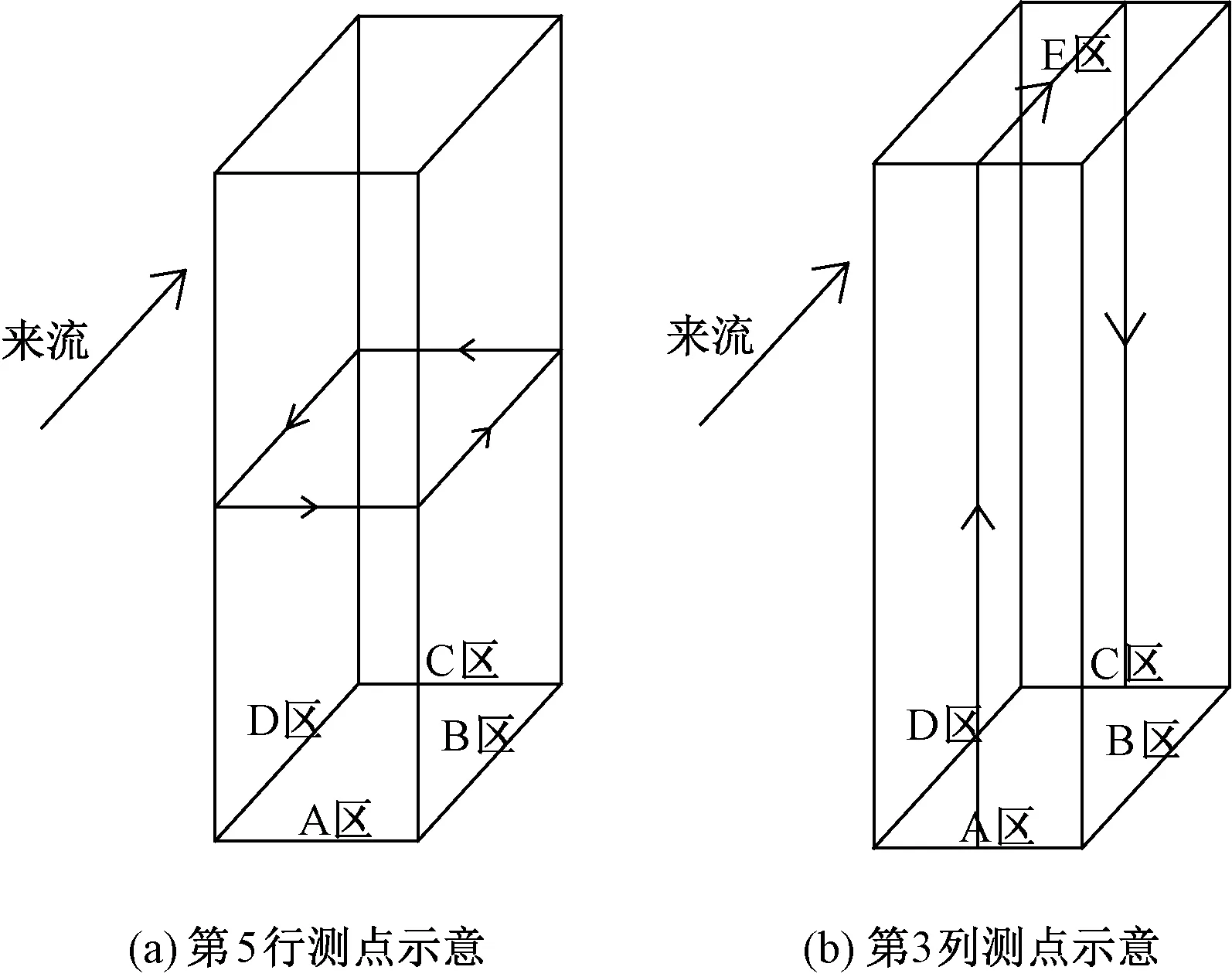
图5　模型第5行与第3列位置示意Fig.5　Measuring point arrangement of the fifth line and the third column of the model

由图6可见,平均风压在迎风面呈中间变化小，两侧变化大的现象.如雷诺数由6.7×104增大到1.33×105，A503测点平均风压由1.20增大到1.22，变化幅度1.67%，位于第5行两侧的A501测点和A505测点变化幅度分别是6.17%和7.14%.第3列也呈中间变化小，顶部和底部变化大的现象，如第3列中部区域A403与A603测点变化幅度分别为0.79%和1.59%，底部区域A103测点减小6.4%，顶部区域A903测点减小5.6%.表明在模型的边界区、棱角区受气流分离等现象影响，平均风压系数对雷诺数更加敏感.与侧风面、背风面比，雷诺数增大2倍，迎风面平均风压系数变化很小，最大变化幅度不超过7%.侧风面雷诺数增大2倍，平均风压系数变化的幅度在10%～20%.背风面变化幅度最大约30%～40%.背风面会受来流紊流、特征紊流、涡脱、再附等因素影响，导致流场最复杂，所以雷诺数效应最明显，这与迎风面不同位置雷诺数效应敏感程度相吻合.

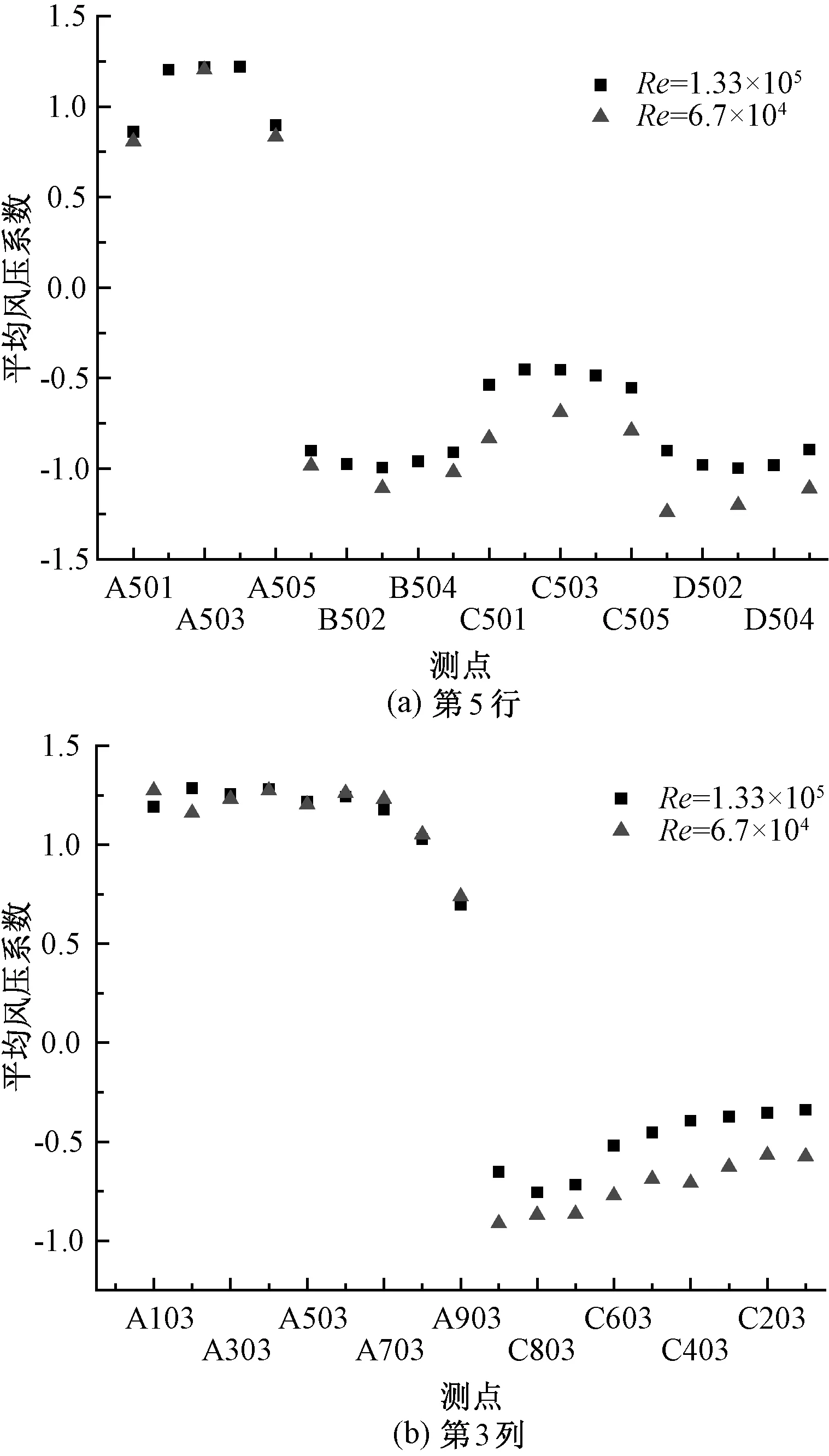
图6　平均风压系数随雷诺数变化情况Fig.6　Variation of mean wind pressure coefficient changing with Reynolds number

2.2　紊流积分尺度对平均风压雷诺数效应的影响

为研究低雷诺数变为高雷诺数后试验数值的波动幅度，定义雷诺效应因子T，如式(2)所示.

Tn(Re1-Re2)=100×Cn(Re2)/Cn(Re1),

(2)

式中：Re1代表低雷诺数;Re2代表高雷诺数.下标n可以为mean、rms、t，分别表示平均风压系数、脉动风压系数、体型系数.

表3为雷诺数增大2倍后，在两种不同积分尺度(紊流强度相同)流场中，第5行与第3列测点平均风压系数雷诺效应因子.由表3可见,在迎风面A区，紊流积分尺度变化对雷诺效应因子影响不明显，平均风压系数在两种不同积分尺度流场中变化幅度很小，最大不超过5%.侧风面B区、D区与背风面C区雷诺效应因子较A区增大，说明在流场较复杂的侧风区与背风区，雷诺数效应会变得较敏感.紊流积分尺度增大，使B区、D区、C区雷诺效应因子增大的幅度变大.侧风面B区、D区不同位置增大幅度约3%～15%，背风面C区增大幅度最大，约10%～20%.说明积分尺度增大会导致雷诺数效应敏感区域的平均风压数值变化幅度进一步增大.雷诺数效应越明显，紊流积分尺度的影响越大.

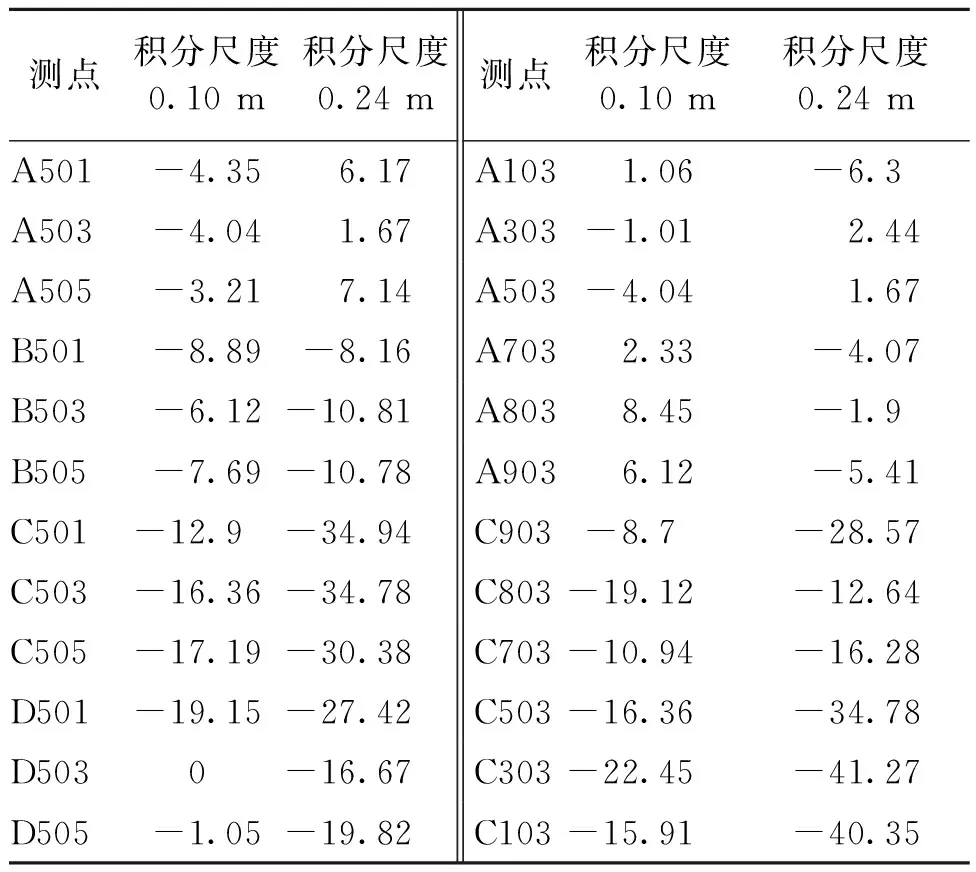
表3　积分尺度对第5行和第3列测点Tmean(6.7×104～1.33×105)影响Tab.3　Effect of integral scale on the Tmean

2.3　紊流强度对平均风压雷诺数效应的影响

表4为雷诺数增大2倍后，在3种不同紊流强度(积分尺度相同)的流场中，矩形结构表面分区体型系数雷诺效应因子，由表4可见,迎风面A区(正压区)雷诺效应因子随紊流强度增大逐渐减小，在紊流强度35%的流场中，迎风面A1～A3区体型系数基本不受雷诺数效应影响，不同尺度模型得到的体型系数基本保持不变.在侧风面、背风面及顶面(负压区)雷诺效应因子均随紊流强度增大而增大，在紊流强度35%的流场中，矩形结构负压区体型系数雷诺数效应比较明显.分析原因，A区处于迎风面，直接受来流紊流的影响，受结构尺度影响较小.侧风面与背风面的负压区除了受来流紊流影响，结构尺度自身造成的特征紊流也会影响.特征紊流受结构外形影响，来流经过结构表面产生涡脱、分离、再附等绕流现象.来流紊流强度越大，造成的特征紊流紊乱程度越强.顶面、背风面、侧风面负压区均会受到绕流、尾流的影响，所以这些区域的体型系数表现出雷诺数效应，结构尺度变化后，导致特征紊流发生变化，从而影响到负压区的体型系数.模型尺度越大，紊流强度变化导致负压区的体型系数变化幅度也越大.

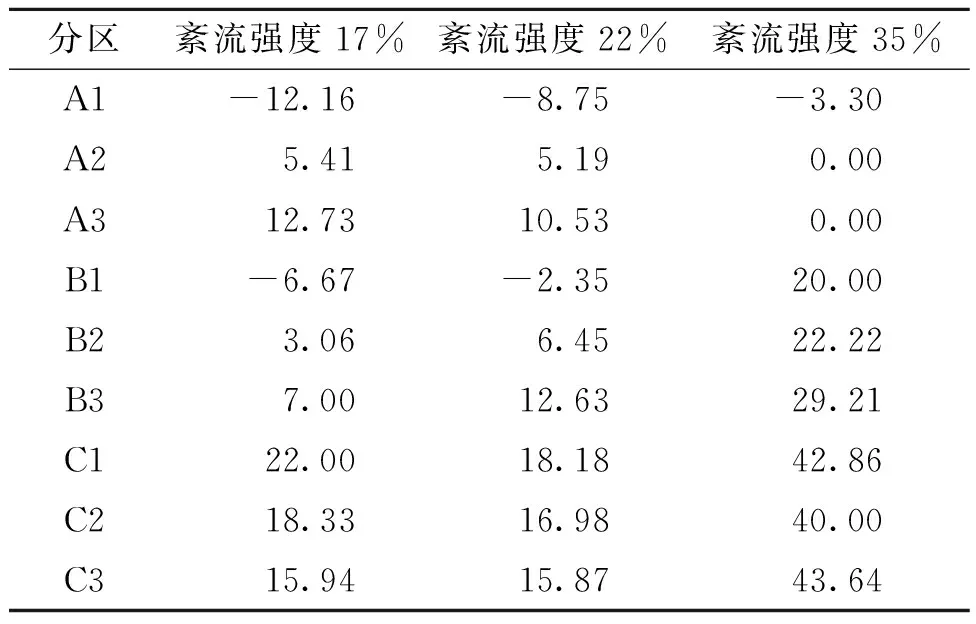
表4　紊流强度对分区体型系数Tt(6.7×104～1.33×105)影响Tab.4　Effect of turbulence intensity on the Tt(6.7×104～1.33×105)of partition shape coefficient

2.4　风场不变时脉动风压雷诺数效应

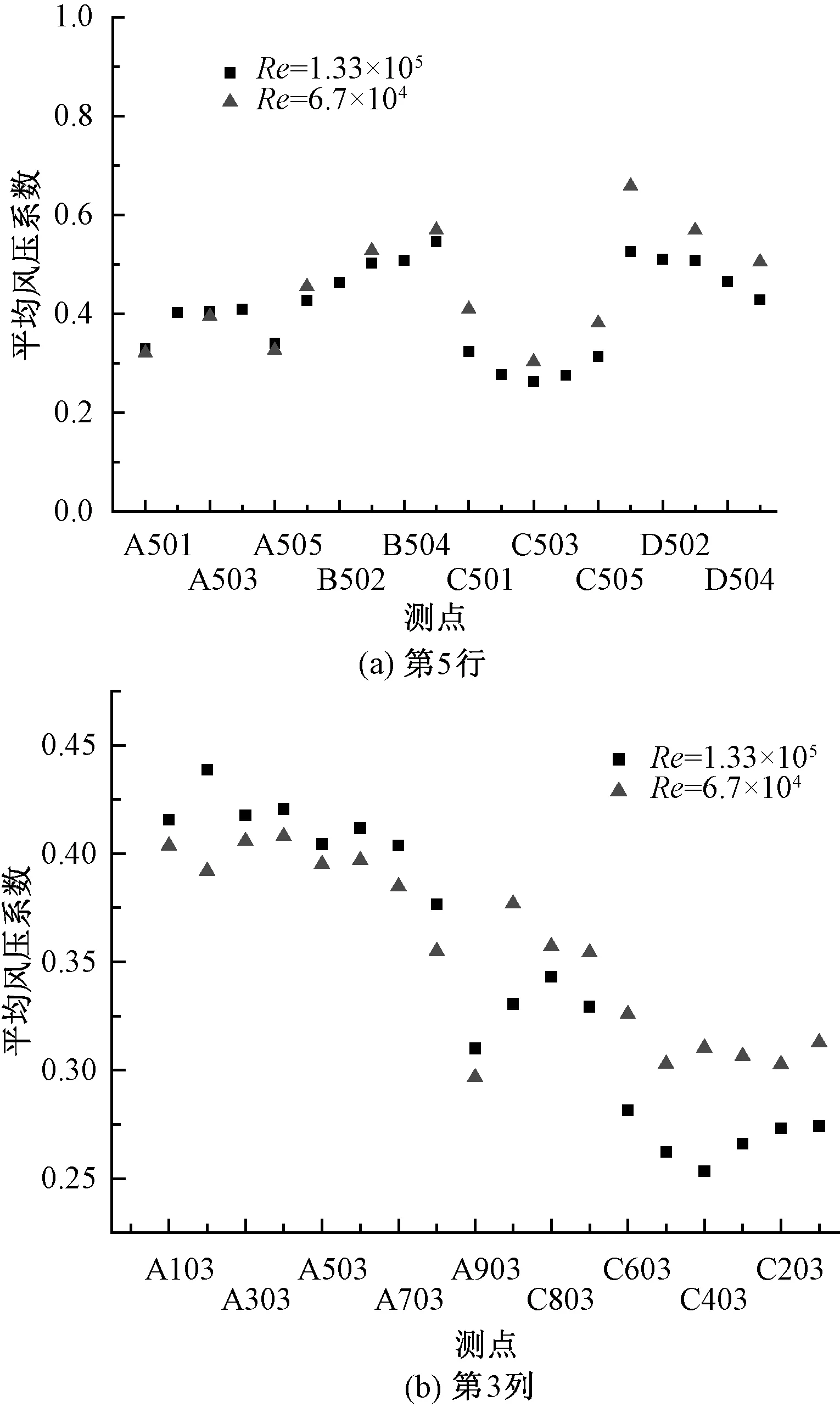
图7　脉动风压系数随雷诺数变化情况Fig.7　Variation of fluctuating wind pressure coefficient changing with Reynolds number

图7为格栅10～20风场中第5行与第3列脉动风压系数随雷诺数变化情况.与平均风压系数雷诺数效应类似，在迎风面脉动风压系数变化幅度很小，最大变化幅度为9.5%，出现在A903测点，迎风面各位置也呈现中间小，两侧及顶部、底部区域稍大的趋势.侧风面与背风面随雷诺数增大脉动风压系数变化幅度较迎风面明显增大，背风面变化幅度稍大于侧风面.负压区的脉动风压系数随雷诺数增大呈减小趋势.脉动风压的雷诺数效应敏感区与平均风压雷诺数效应敏感区一致.

2.5　紊流积分尺度对脉动风压雷诺数效应的影响

表5为雷诺数增大2倍后，积分尺度变化对第5行与第3列测点脉动风压系数雷诺效应因子的影响.由表5可见，积分尺度变化后，迎风面脉动风压系数雷诺效应因子均不大.迎风面中部区域当来流积分尺度为0.10 m时，脉动风压系数随雷诺数增大而减小，积分尺度增大为0.24 m时，脉动风压系数随雷诺数增大而增大.分析原因，从积分尺度与模型尺寸比例关系看，小模型的横截面尺寸是0.10 m的正方形，所以0.10 m与0.24 m的来流紊流积分尺度均比模型的特征尺寸大，可以将模型“包裹”起来.大模型的特征尺寸是0.20 m，是0.10 m积分尺度的2倍，这就导致0.10 m的来流积分尺度无法完全覆盖大模型，积分尺度所形成的涡团影响范围与模型尺寸之间的相对比例关系发生变化，导致涡脱、再附等流场影响区域发生变化，导致大、小模型迎风面不同区域雷诺效应因子变化趋势产生差异.

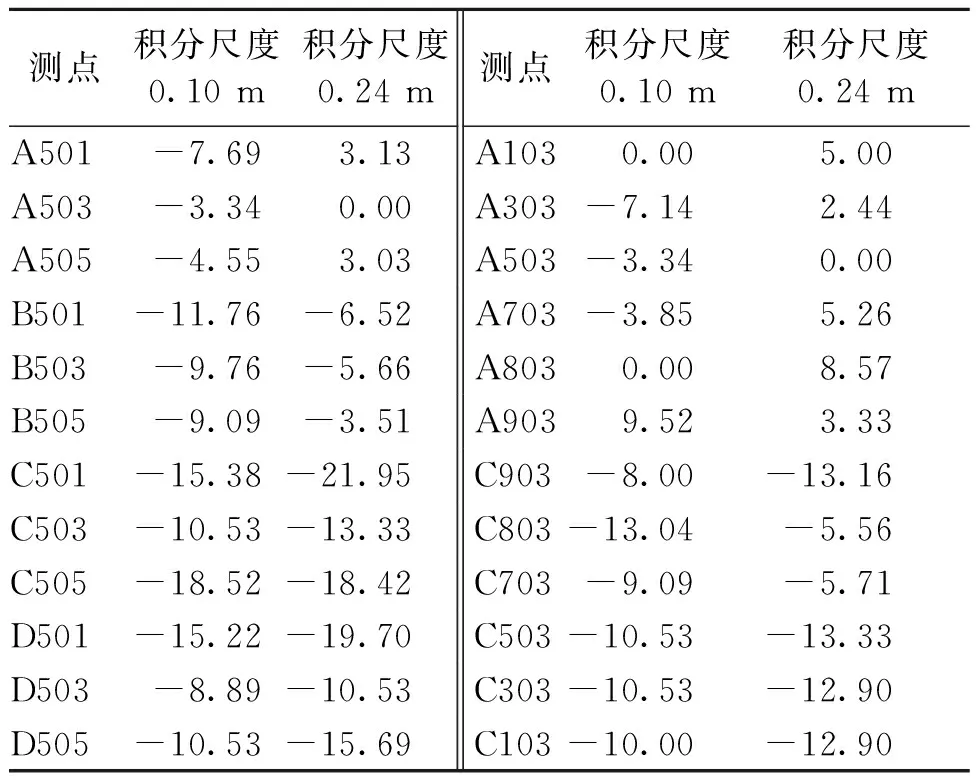
表5　积分尺度对第5行和第3列测点Trms(6.7×104～1.33×105)影响Tab.5　Effect of integral scale on the Trms(6.7×104～1.33×105) of measuring point in fifth line andthird column

侧风面与背风面负压区的脉动风压系数随雷诺数增大呈减小趋势.来流积分尺度增大会导致脉动风压变化的幅度稍微增大，与积分尺度对平均风压雷诺效应因子影响相比，积分尺度变化对脉动风压的影响程度较平均风压小，尤其是背风面.

2.6　紊流强度对脉动风压雷诺数效应的影响

图8为紊流强度对矩形结构分区脉动风压系数的影响，由图8可见，增大紊流强度会使各区脉动风压系数也增大.背风面与侧风面脉动风压系数增大的幅度明显较迎风面小.迎风面顶部A3区域的脉动风压系数随紊流强度的变化幅度最大，位置越高对紊流强度变化越敏感.矩形结构迎风面中上部位置是正压极值出现的位置，而此区域的脉动风压系数对紊流强度非常敏感，所以试验时紊流强度的不当模拟可能导致脉动风压结果误差增大.背风面脉动风压系数对紊流强度的敏感程度最小，侧风面敏感程度居于两者之间.

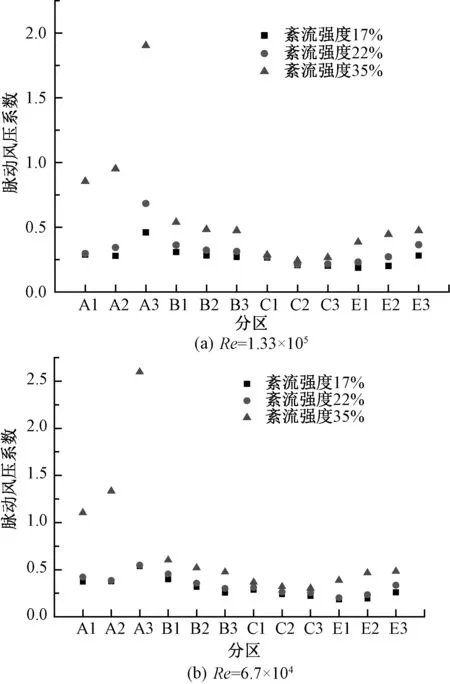
图8　不同分区脉动风压系数Fig.8　Fluctuating wind pressure coefficient of different partition

图9为紊流强度对迎风面与背风面测点脉动风压时程影响情况，由图9可见，背风面脉动风压系数对紊流强度的敏感程度较迎风面小很多.A905测点处于顶角边缘位置，此处会受到涡脱、边界层分离、再附等特征紊流影响，所以对来流紊流强度非常敏感.矩形结构外形简单，特征紊流影响的范围与程度相对较小.对外形更加复杂的结构，可以预测风洞试验时紊流强度模拟误差会导致更大的脉动风压系数误差.

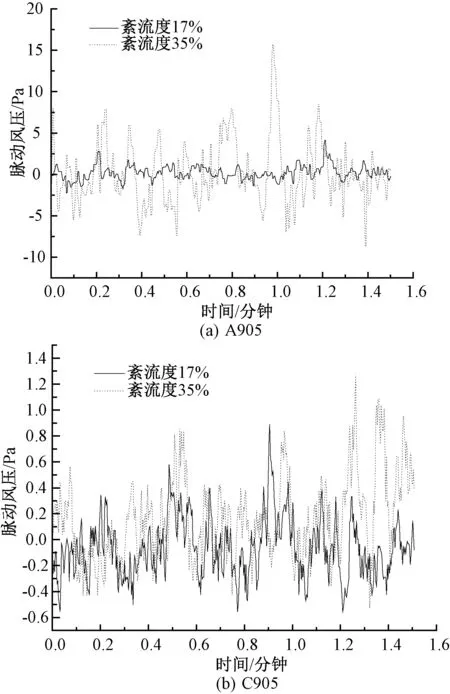
图9　迎风面与背风面测点脉动风压时程Fig.9　Time history of fluctuating wind pressure on the windward and leeward sides

表6为雷诺数增大2倍后，紊流强度变化对脉动风压系数雷诺效应因子的影响.由表6可见，迎风面脉动风压雷诺效应因子较侧风面与背风面大.紊流强度增大后使脉动风压系数增大的幅度

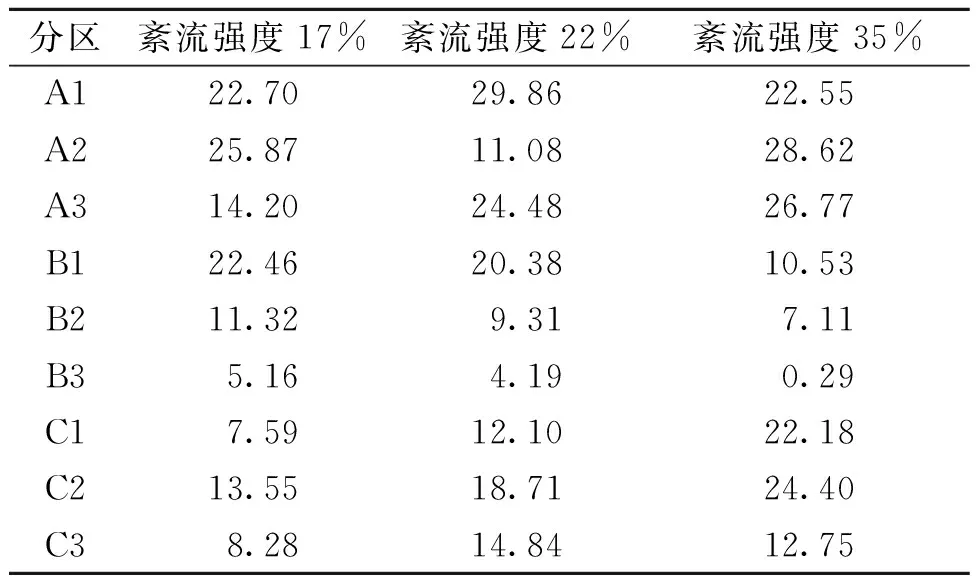
表6　紊流强度对分区脉动风压系数Trms(6.7×104～1.33×105)影响Tab.6　Effect of turbulence intensity on the Trms

没有明显规律，基本不受模型尺度影响，表明紊流强度对脉动风压系数雷诺数效应影响很小.矩形结构表面不同位置脉动风压对紊流强度的敏感程度不同，脉动风压大小主要取决于来流紊流强度，与模型尺度无关.

3　结论

(1)平均风压与脉动风压雷诺数效应在迎风面最小，背风面最大，侧风面次之.

(2)积分尺度增大会导致雷诺数效应敏感区域的平均风压数值变化幅度进一步增大.雷诺数效应越明显，紊流积分尺度的影响越大.

(3)来流紊流强度越大，模型负压区平均风压系数的雷诺数效应越大；模型尺度越大，紊流强度变化导致负压区的体型系数变化幅度也越大.

参考文献：

[1]李加新, 林志兴, 项海帆. 极端桥梁断面雷诺数效应研究[J]. 郑州大学学报(工学版)，2003，24(2):22-25.

[2]BARRE C, BARNAUD G. High Reynolds number simulation techniques and their application to shaped strucutures model test, wind Engineering Thomas Telford,London,1993.

[3]金挺, 林志兴. 扁平箱形桥梁断面斯特罗哈数的雷诺数效应研究[J]. 工程力学, 2006,23(10)：174-179.

[4]SCHEWE G. Reynolds number effects in flow around more-or-less bluff bodies[J]. Journal of wind engineering and industrial aerodynamic, 2001,89(2):91-97.

[5]TIELEMAN H W. Wind tunnel simulation of the turbulence in the surface layer, the proceedings of the 6thU.S. National Conference on Wind Eng. Vol.2 March 8-10 1989 Univ.of Houston.

[6]HURST E, YANG Q, CHUNG Y M. The effect of Reynolds number on turbulent drag reduction by streamwise travelling waves[J]. Journal of Fluid Mechanics, 2014,759(12):28-55.

[7]MATSUBARA M, HORII S, YOSHIYUKI S, et al. Very-large-scale fluctuations in turbulent channel flow at low Reynolds number[J]. International journal of heat and fluid flow, 2016,31(1):12-18.

[8]李加武, 张宏杰, 韩万水. 斜拉桥风致响应的雷诺数效应[J]. 中国公路学报, 2009,22(2):42-47.

[9]白桦. 影响桥梁及建筑结构风洞试验结果若干因素研究[D]. 西安：长安大学公路学院，2012.

[10] 华旭刚, 陈政清, 杨靖波, 等. 大缩尺比气弹模型风洞试验紊流积分尺度修正[J]. 建筑结构学报, 2010,31(10): 55-61.

[11] 卢占斌, 魏庆鼎. 网格紊流CAARC模型风洞实验[J]. 空气动力学学报. 2001,19(3):16-23.