基于FAST特征点改进的TLD目标跟踪算法

毛晓波， 周晓东， 刘艳红

(郑州大学 电气工程学院，河南 郑州 450001)

0　引言

目标跟踪是计算机视觉领域的重要研究内容，可以理解为在已知目标先验信息情况下，在视频序列中持续地对目标的位置、形状和运动状态进行发现的过程.同时，目标跟踪也一直是计算机视觉的难点之一[1]，除了光照变化，障碍物遮挡等环境影响，目标本身的旋转、尺度变化及出视野都对准确地进行目标跟踪造成挑战.

近些年来，国内外的研究人员根据实际需要提出和实现了多种跟踪算法.如meanshift[2]、卡尔曼滤波[3]、粒子滤波[4]等算法，它们针对特定的场景都有较好的效果.我们注意到上述算法在跟踪过程中，随着跟踪误差的逐渐增大及目标本身的大小、形态改变，尤其是当目标离开视野后又重新回到视野时，都会造成跟踪失败.这种随着跟踪时间的延长逐渐导致跟踪失败的算法称为短时跟踪算法.为了解决这一问题，与之对应的长时间跟踪算法是我们研究的重点.为了避免随着时间推移导致跟踪失败，长时间跟踪算法应该至少具有以下两个特点，一是能够在跟踪过程中逐渐地减少或保持跟踪误差；二是在完全遮挡或是出视野造成跟踪失败后，具有对目标的重识别能力.

TLD(tracking-learning-detection)算法[5]是近年来十分具有代表性的长时间跟踪算法,它将传统的跟踪算法和检测算法结合起来，同时引入在线学习机制，三者并行运行，实现长时间跟踪.然而该算法也存在明显的不足，如:算法计算量大，运行帧率达不到实时应用的标准；跟踪器均匀选取的点，在跟踪中可靠性不高；跟踪过程中模板累积效应明显，后期运行速率越来越慢等.针对TLD算法的缺点，已有许多学者提出改进的方法.周鑫[6]和董永坤[7]分别对TLD的检测部分进行改进，提高了跟踪效果，然而算法的最终输出结果是跟踪器和检测器返回目标框的融合，且跟踪器的结果在TLD融合部分占比更大.文献[8]指出，提高跟踪器的可靠性将对算法整体准确性和鲁棒性提供积极的影响.邢藏菊[9]对跟踪器的归一化互相关匹配进行改进，减少了跟踪器的计算量，同时降低了误匹配率，也取得了不错的效果.所以针对跟踪器的不足，对其进行改进也是具有重要研究意义的.

针对TLD算法中，跟踪器均匀选取的点无法在下一步的中值光流法中保证准确跟踪的问题，笔者提出采用快速检测的FAST特征点替代跟踪器中均匀选取的点，保证选取点的稳定准确跟踪，提高算法的准确性和实时性.针对跟踪后期由于模板累积使得算法后期的匹配过程耗时增加，实时性降低的问题，采用一种动态的模板管理机制，使得模板总量保持稳定，提高算法后期的实时性.

1　TLD算法与分析

1.1　TLD算法简介

TLD算法是由Kalal等人于2010年提出的新型跟踪算法，结构如图1所示.

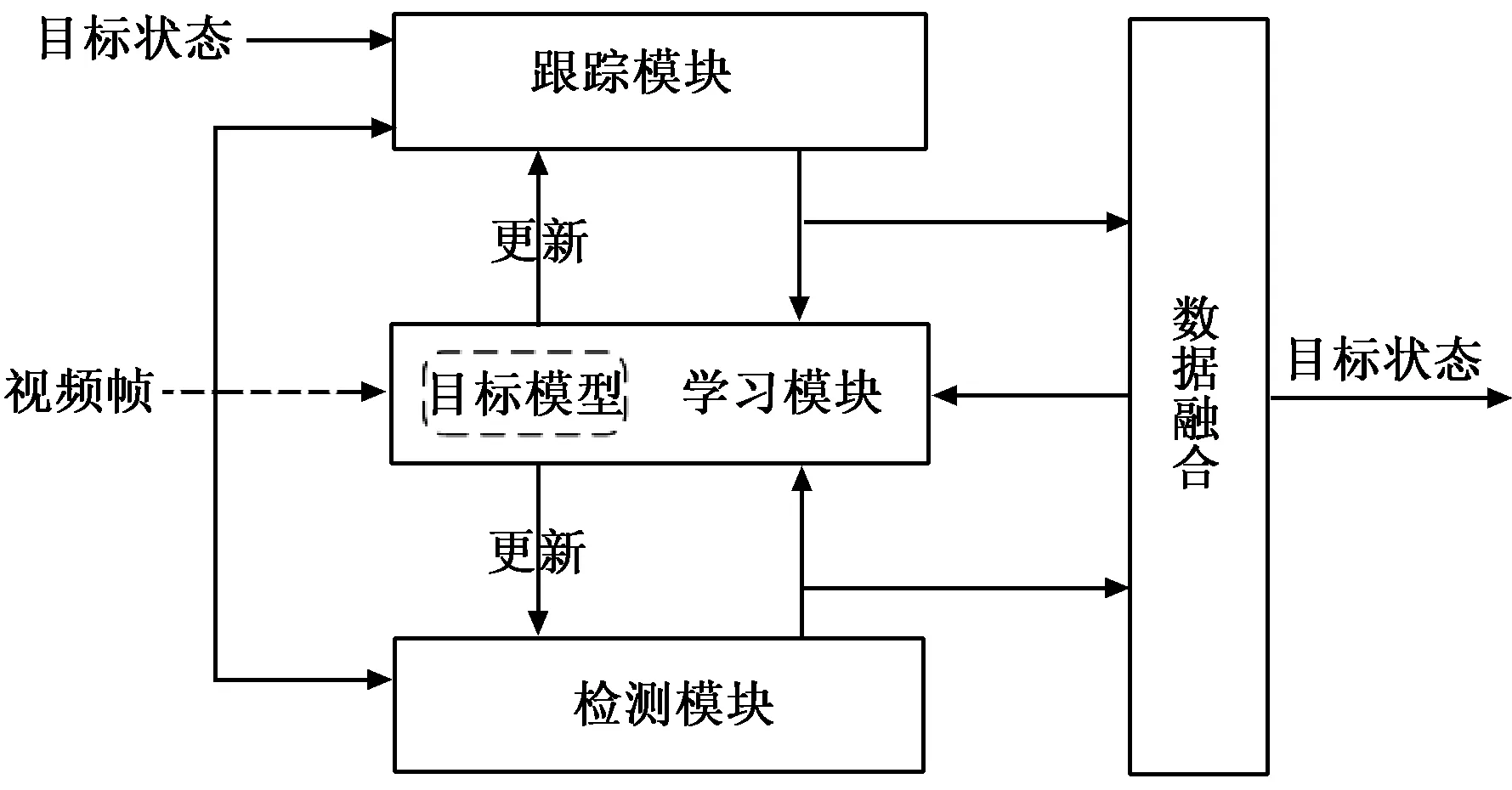
图1　TLD算法示意图Fig.1　TLD algorithm

TLD跟踪模块的本质是中值流跟踪，是一种增加了跟踪失败校验的LK光流法.跟踪模块根据所选目标确定边界框，并在框内生成10×10的矩形网格，以每个网格的中心位置作为跟踪的特征点，对应一个局部的跟踪器.每个跟踪器采用LK光流法跟踪特征点的运动，由于LK光流法3个假设[10]的局限性，当目标完全遮挡或者出视野后，将出现跟踪偏移.由此，采用一种跟踪误差检测机制，通过计算当前图像和被跟踪区域的相似程度(normalized cross correlation，NCC)及前向后向误差(forward-backward error，FB)对每个点的跟踪质量进行评估，去除误差排名前50%的点，使用余下的点来评估边界框的状态改变情况，生成新的跟踪窗口，完成一次短期跟踪.

检测模块采用不同尺度的滑动窗口扫描整幅图像，将扫描产生的大量窗口送入级联分类器判别是否存在前景目标.级联分类器由3部分组成，依次是方差分类器、集合分类器和最近邻分类器.只有当窗口内的图像依次通过上述3种分类器时，窗口才被认为含有前景目标.

学习模块在第一帧初始化检测器，随后采用P-N专家产生的正负模板训练检测器.使用P专家来寻找目标新的外观变化，使用N专家确定检测器应该忽略的背景部分.通过P-N专家的相互作用，提高样本标记的准确性，并在运行时实时更新检测器.在算法的运行过程中，通过检测模块和跟踪模块并行运行，更新目标信息，减少跟踪误差.通过在线学习模块，对产生的新样本进行标签学习，更新检测器.当完全遮挡或者出视野等导致跟踪失败时，由于检测模块的全局扫描能力，在跟踪目标重回视野后具有重识别能力，3种模块相互配合，共同实现目标的长时间跟踪.

1.2　缺陷分析及改进

从上节可以看出，TLD跟踪算法相对于传统的跟踪算法在长时间目标跟踪上具有较大的优势，然而它也有许多不足之处，下面对它的一些缺陷进行分析并提出改进方法.

1.2.1跟踪模块分析及改进

尽管这种中值流跟踪方式在实际应用中取得了不错的跟踪效果，但是从理论分析来看，在目标上均匀地选取固定数目的特征点并不能保证这些点能可靠地被LK光流法进行跟踪，若选取的特征点处于灰度值变化平缓或者无变化的区域，将给光流法跟踪带来很大的问题.同时如果这些选出的点不能被可靠跟踪，那么也将影响目标跟踪的效率和准确性.针对该问题，笔者采用可用于快速检测的特征角点来替代原算法中均匀选取的点，以获得对目标更好的表观能力，保证可靠跟踪.

常用的特征角点有SIFT(scale-invariant feature transform)[11]，SURF(speed up robust features)[12]，Harris[13]，FAST(features from accelerated segment test)[14]及BRISK(binary robust invariant scalable key points)[15]等.其中Harris和FAST特征点是简单的单尺度角点，而SIFT、SURF和BRISK是多尺度特征点，在生成方式上除极值检测外，还需要构造尺度空间、滤波及生成描述子，因此在检测速度上要远低于单尺度角点.多尺度特征点的优点在于对尺度变化不敏感，具有尺度不变性，同时对旋转和亮度变化能保持较强的鲁棒性.借助opencv图像处理库，在待测图片为Eiffe,大小为925×650时，上述算子的检测时间和检测点数如表1所示.经过对比可知，Harris和FAST特征角点的检测速度远远超过多尺度特征点的检测速度，印证了上面的分析.前向后向算法对角点的尺度变化并不敏感.文献[15]指出Harris的角点稳定性与经验值k有关，k值不好确定且浮动较大，这就意味着对于一个跟踪目标，经过多次尝试效果较好的k值对另一目标很有可能效果十分糟糕，这种情形将极大地降低算法的稳定性.对于跟踪目标来说，目标框通常只是图像整体很小的一部分，表1表明FAST角点的检出率比Harris高出一个数量级.

表1　特征角点检测对比

在实际检测中，目标框的FAST角点数最少时仅几十个，如采用Harris获取的角点数目只有个位量级，对于后续的跟踪算法来说太过稀少，所以应选取能检测较多角点的算法.由此，笔者采用FAST特征点来取代原算法中均匀选取的点.

FAST特征点是Rosten等人在SUSAN角点特征检测方法的基础上，利用机器学习方法提出的,其主要特点是检测速度快.最初的检测方法就是检测在圆环上的16个像素点，如果有n个连续的点比中心像素m的强度都大或都小的话，这样的中心点就是角点.我们采用FAST-9角点检测算法，每个像素m周围的像素mi,i∈{1,2,…,16}的灰度值如图2所示，按式(1)将像素m分为3类.

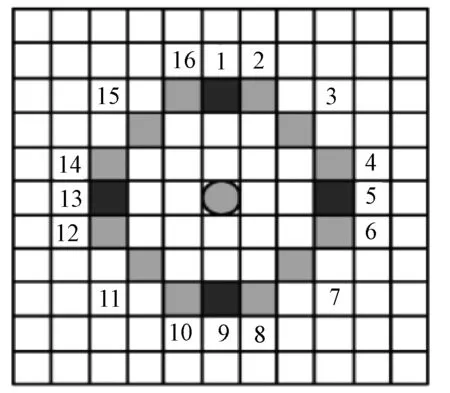
图2　FAST检测邻域图Fig.2　Schematic diagram of FAST detection field

(1)

式中：Im表示m点的像素值；Im→i表示m点第i个邻接像素点的像素值；d表示邻接像素点比m点暗；s表示邻接像素点与m有相似的像素值；b表示邻接像素点比m点亮.n为检测阈值，当至少有9个邻接的参考像素检测结果均为d或b时，则m点为FAST角点.

在获取了跟踪框内目标的FAST特征点后，将获得的点送入后续的中值光流法中进行跟踪，跟踪模块结构如图3所示.

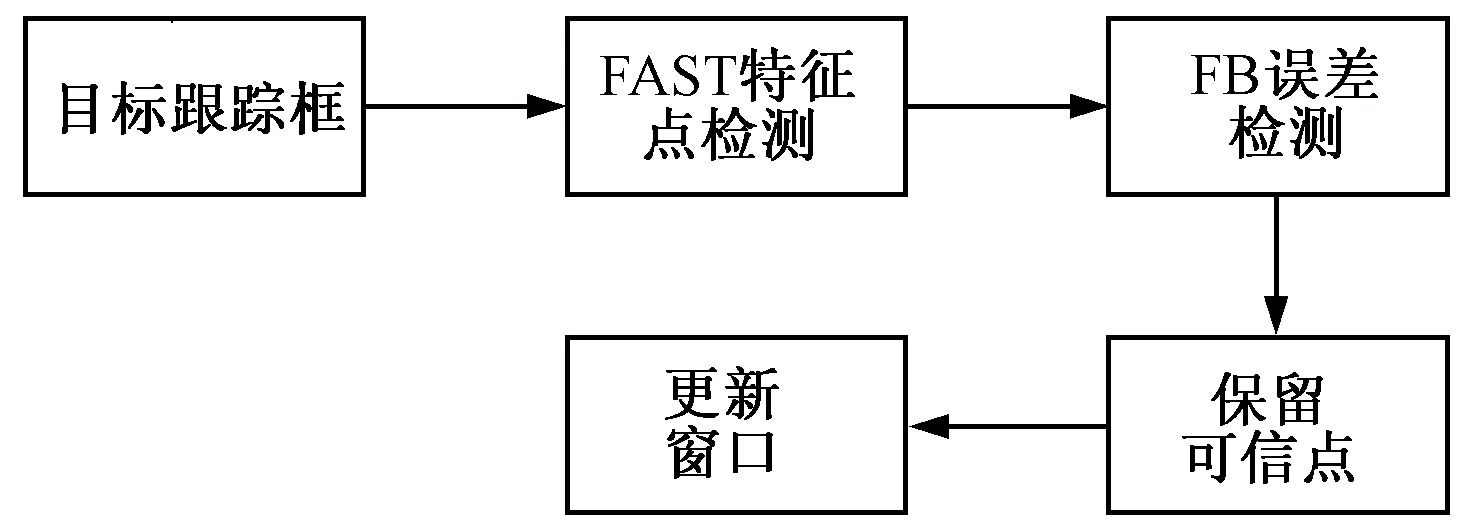
图3　跟踪模块图Fig.3　Tracking module

1.2.2模板累积改进

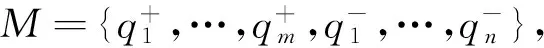
S(pi,M)=0.5(NCC(pi,M)+1),

(2)

则图像区域和目标区域的最终相似度为

(3)

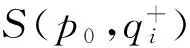
2　试验结果分析

为验证改进算法性能，将原始TLD(称TLD)算法、笔者改进的TLD算法(称TLD+)和文献[16]中采用的具有旋转不变性和尺度不变性的BRISK角点改进TLD算法(称BTLD)做对比.测试环境为I7-4720HQ @ 2.6 GHz 8 G内存的Win10 64位计算机，试验软件为Visual Studio 2015和opencv 3.1.0.测试集为公开的视频序列Motocross、Car、David、pedestrian2和Singer1，包含了目标遮挡、光照变化、尺度变化、出视野等情形.定义两个具有代表性的评估准则：①跟踪成功率(success rate,SR)，是指成功跟踪的帧数占总帧数的比例，当跟踪框与手工标定的目标框重合率在50%以上时，称为一次成功跟踪;②帧率(frame per second,FPS)指每秒处理的帧数，反映算法运行速度.

设定FAST特征点的检测阈值n=24，最近邻分类器的阈值θ=0.6，前向后向误差的阈值FBr=10.另外为了保证试验的客观性，采用笔者方式指定初始化目标跟踪框，其余未改进的参数均采用算法原来的参数，BTLD与笔者改进算法区别仅在于跟踪模块特征点的产生方式不同.表2为TLD算法和两种改进算法的跟踪准确率对比.表3为3种算法运行帧率对比.

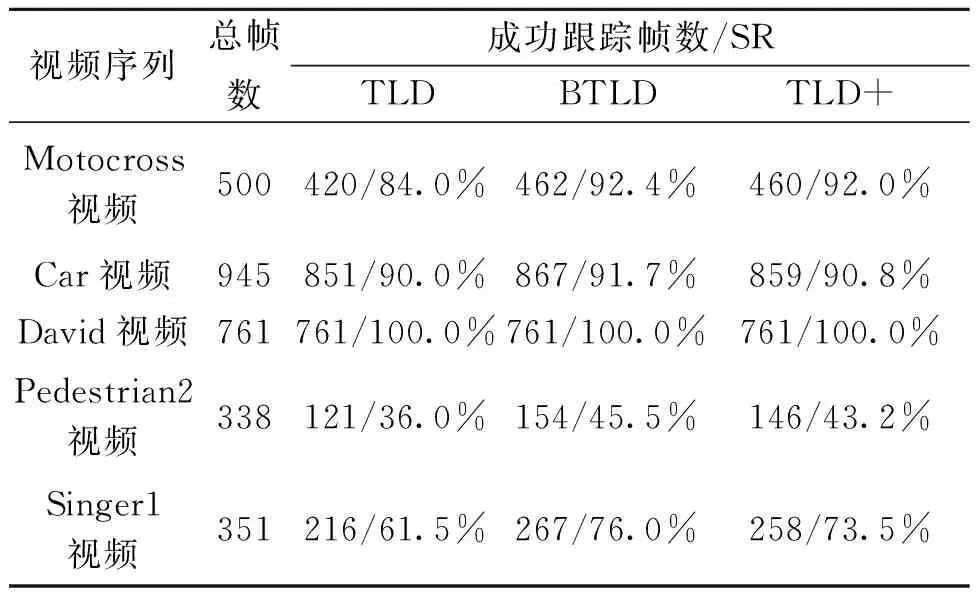
表2　算法跟踪准确率比较

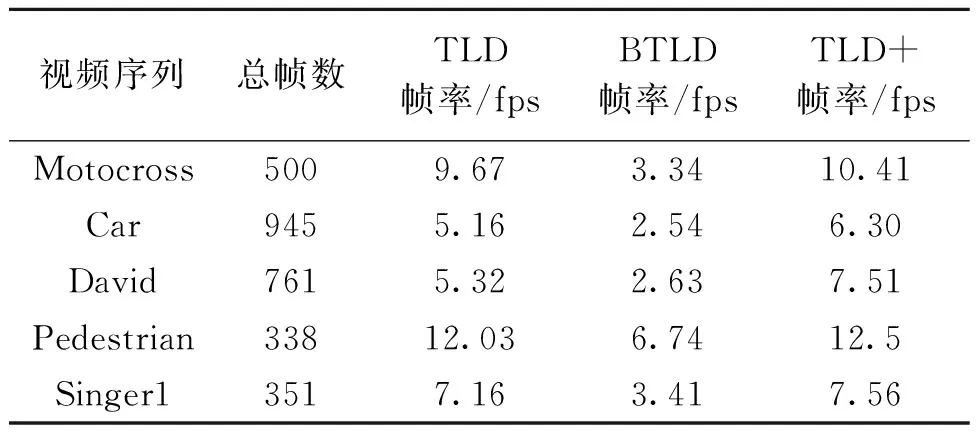
表3　算法运行帧率比较Tab.3　Tracking FPS comparison

由表2可以看出，TLD+的跟踪准确率高于原TLD算法，而略低于BTLD算法.这是由于FAST特征点不具有BRISK的尺度不变性，相对来说对噪声较为敏感.两者差距不大是因为选取的特征点只是参与到后续的光流跟踪中，并不涉及特征点匹配.TLD+和BTLD算法在跟踪精度上与原算法相比都有提高.图4反映了原TLD算法和TLD+算法在跟踪视频序列目标时的差异.第一组(红色跟踪框)表示原TLD算法跟踪情况，第二组(蓝色跟踪框)为同一帧TLD+跟踪情况.

图4　算法跟踪差异Fig.4　Tracking algorithms differences

视频Motocross中,在目标平稳运动情况下，原TLD算法和改进的TLD+算法都可以稳定跟踪.在目标发生较大倾斜、抖动情况下，原始的算法因为均匀选取的特征点无法有效表述目标特征，导致跟踪失败，而改进的TLD+由于稳定性较强的角点，依然可以进行跟踪.在视频Pedestrian2中，视频的分辨率较低，存在较为严重的镜头晃动和出视野情况，原算法在目标发生形变及出视野后，不能有效地对后续的目标进行识别，而改进后的算法能在出视野前后有效跟踪目标.Singer1视频中光照变化明显，原算法在目标被强光覆盖后无法继续有效跟踪，改进的算法借助对光照不敏感的特征角点仍然可以进行跟踪.以上试验表明，结合FAST特征点的TLD算法可以有效应对目标抖动、偏移、光照变化造成的跟踪失败，相比于原算法具有更好的鲁棒性.

从表3可得，改进的TLD+在实时性上优于原算法和BTLD.由于BTLD中特征点采用具有抗噪及旋转尺度不变的BRISK特征，其计算过程需要构造尺度空间及滤波的过程，因此虽然提升了准确性，但严重牺牲了实时性能.TLD+的模板累积改进对于跟踪模板数量较多的情况具有较好的效果.一般来说模板的数量取决于跟踪的时间和跟踪目标变化的差异程度.对于Pedestrian2和Singer1帧数较少的视频序列，模板数量尚达不到阈值要求，因此模板累计改进对它们的帧率基本没有影响.对于Car视频序列，虽然帧数较多，但目标车辆形态缺乏变化，所获取的模板数量仍然不多，故而改进对于Car视频序列的实时性提高较为有限，而在David视频序列中，具有较强的光照变化，目标的状态变化十分明显，因此获得的模板数量较多，改进算法的实时性提升较为明显.

3　结论

TLD是近年来较为新颖的长时间跟踪算法，笔者在它的基础上引入FAST特征点取代跟踪模块中均匀选取的点，提高跟踪的鲁棒性.对其因模板累积导致的实时性降低问题，采用动态的模板替换更新机制，经过多个视频测试集测试表明，笔者算法相比于原算法在跟踪准确性和实时性方面均有小幅提高，相比于BRISK特征点改进的TLD算法，准确性与其差异微小，实时性取得较大的提高.

参考文献：

[1]高文, 朱明, 贺柏根,等. 目标跟踪技术综述[J]. 中国光学, 2014, 7(3):365-375.

[2]郝向东,毛晓波,梁静.ELM与Mean Shift相结合的抗遮挡目标跟踪算法[J].郑州大学学报(工学版),2016,37(1):1-5.

[3]WENG S K, KUO C M, TU S K. Video object tracking using adaptive kalman filter[J]. Journal of visual communication & image representation, 2006, 17(6):1190-1208.

[4]宋策. 基于粒子滤波的目标跟踪技术研究[D]. 长春：中国科学院大学长春光学精密机械与物理研究所, 2014.

[5]KALAL Z, MIKOLAJCZYK K, MATAS J. Forward-backward error: automatic detection of tracking failures[C]// International Conference on Pattern Recognition, IEEE Computer Society, Turkey: Lstanbul, 2010:2756-2759.

[6]周鑫, 钱秋朦, 叶永强,等. 改进后的TLD视频目标跟踪方法[J]. 中国图象图形学报, 2013, 18(9):1115-1123.

[7]董永坤, 王春香, 薛林继,等. 基于TLD框架的行人检测和跟踪[J]. 华中科技大学学报(自然科学版), 2013, 41(s1):226-228.

[8]秦飞, 汪荣贵, 梁启香,等. 基于关键特征点的改进TLD目标跟踪算法研究[J]. 计算机工程与应用, 2016, 52(4):181-187.

[9]邢藏菊, 温兰兰, 何苏勤. TLD视频目标跟踪器快速匹配的研究[J]. 小型微型计算机系统, 2015, 36(5):1113-1116.

[10] BIRCHFIELD S. Derivation of kanade-lucas-tomasi tracking equation[J]. Unpublished notes, 1997, 44(5): 1811-1843.

[11] LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International journal of computer vision, 2004, 60(2):91-110.

[12] BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features[J]. Computer vision & image understanding, 2008, 110(3):404-417.

[13] HARRIS C. A combined corner and edge detector[J]. Proc alvey vision conf, 1988, 15(3):147-151.

[14] ROSTEN E, DRUMMOND T. Machine learning for high-speed corner detection[C]// European Conference on Computer Vision. Berlin: Heide berg, 2006:430-443.

[15] LEUTENEGGER S, CHLI M, SIEGWART R Y. BRISK: binary robust invariant scalable keypoints[J]. Computer vision (ICCV), 2011, 58(11):2548-2555.

[16] 祝贤坦, 石繁槐. 基于BRISK特征点改进的跟踪学习检测方法[J]. 计算机工程,2017,43(2):268-272.