新型四足步行机器人串并混联腿的轨迹规划与仿真研究

高建设，王玉闯，刘德平，王保糖

(郑州大学 机电一体化研究所，河南 郑州 450001)

0　前言

由于仿生机器人同时具有生物和机器人的特点，所以逐渐在反恐防爆、抢险救灾等不适合由人来承担任务的环境中表现出良好的应用前景[1-2].步行机器人由于落足点离散，在其足端能够达到的范围内可以灵活调整行走姿态，并合理选择支撑点，所以对复杂地形和非结构化环境具有更强的适应能力[3]，目前已成为机器人研究的热点领域之一.

在四足机器人中，其腿部机构多数是串联的，比较典型的有美国波士顿动力学公司的BigDog、猎豹Cheetah和野猫Wildcat等.这些机器人腿的结构简单，建模和控制比较容易，但自重载重比大，承载能力相对较低.也有学者利用并联腿机构来设计仿生机器人，如上海交通大学提出的六足步行机器人的每条腿都是一种典型3-DOF的并联机构[4]，燕山大学王洪波等基于并联机构提出了四足两足可重组步行机器人[5].虽然并联腿机构有自重载重比小、承载能力强、稳定性高的特点，但是有工作空间小的缺点.为了克服串联或者并联腿各自的不足，国内外一些学者对混联机构做了研究.在四足仿生机器人方面，田兴华等[6]提出了3种类型的3自由度混联腿构型，建立了各自运动学模型和工作空间模型，并证实了混联腿的优越性.

另一方面，步行机器人的轨迹规划是机器人能否平稳运动的重要问题.山东大学的李华[7]和南京航空航天大学的马东兴等[8]都是对关节空间进行规划控制，分别实现了步态行走和定点转弯步态.基于足端轨迹的步态规划是比较常用的方法，最为典型的是基于复合摆线的足端轨迹规划方法.文献[9]提出了基于摆线的足端轨迹规划方法，实现了四足机器人walk步态的行走.东北大学柳洪义等在1994年用修正组合摆线作为足端轨迹规划，解决了足端对不平地面的自适应问题，避免了抬腿时的急动[10].北京理工大学王立鹏等[11]又对复合摆线进行了改进，降低了足端在行走过程中的冲击力.山东大学荣学文等[12]用了三次多项式作为摆动相的足端轨迹.华中科技大学程品等[13]采用五次多项式对足端摆动相轨迹进行了规划.

笔者使用基于高次多项式的零冲击轨迹规划算法对一种新型四足步行机器人的串并混联腿进行规划，并对其进行仿真研究，仿真结果验证了足端轨迹的正确性和合理性，为整机的轨迹规划和步态规划研究奠定了基础.

1　四足机器人机构描述

提出了一种新型四足步行机器人，其结构如图1所示.该机器人由4个完全相同的机器人腿部机构和运载平台组成.

图1　四足机器人样机Fig.1　The prototype of a quadruped robot

图2为腿部机构，图3为髋关节.每条腿部机构均是由髋关节和膝关节组成，其中髋关节由3-RRR并联机构构成，该并联机构的3个分支九个转动副的轴线相交于动平台的中心，动平台能够实现3个转动自由度；膝关节由大腿和小腿通过转动副连接，这样就能实现整个腿部机构运动所需的4个运动自由度.髋关节采用并联机构，一方面可以提高承载能力；另一方面将3个分支的驱动电机装在背部平台上，可以减轻抬腿运动时的运动惯量，使腿部机构运动轻便灵活.用直线运动电缸实现膝关节的转动运动，增大了膝关节的驱动力矩，提高了膝关节的承载能力.

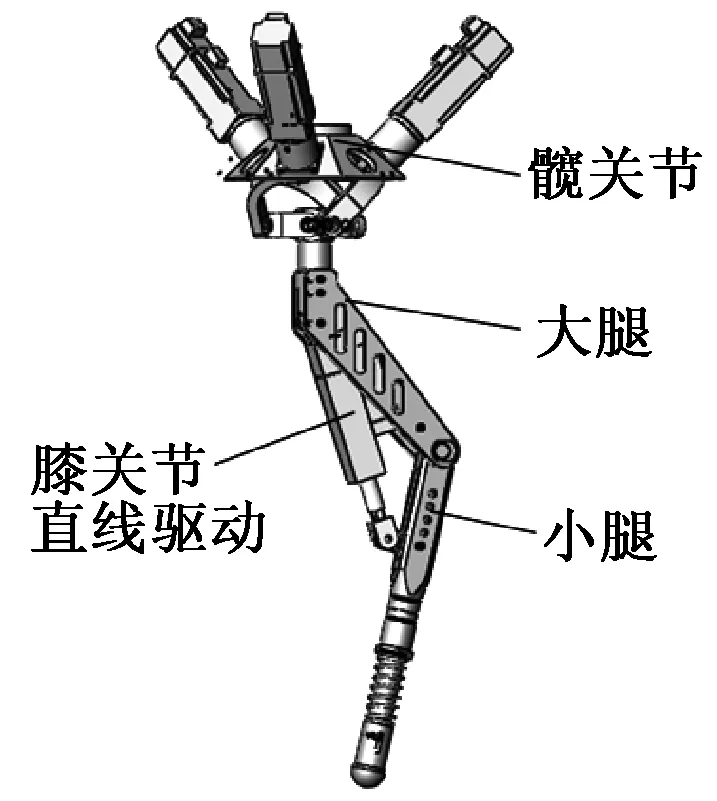
图2　腿部Fig.2　Leg

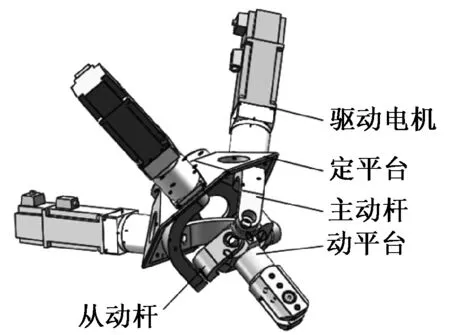
图3　髋关节Fig.3　Hip joint

2　单腿运动学反解模型

首先建立髋关节的坐标系，再来建立整条腿的坐标系.由于髋关节3个分支完全相同，并且相互之间相差120°，因此，可用D-H方法对其第i(i=1,2,3)个分支建立坐标系，如图4所示.{A}为定平台坐标系，{B}为动平台坐标系，初始位置时两个坐标系重合.图中的{Ai}、{Bi}、{1}、{2}和{3}坐标系的原点都与动平台的中心重合.为了便于表达，将各个坐标系移到各关节的中心点处.

再把髋关节等效成一个球副，与膝关节构成串联机构，则腿部坐标系的建立如图5所示.图5中{A}和{B}与图4中完全一样，{C}为膝关节坐标系，L1和L2分别为大腿和小腿长度.{G}为世界坐标系，并设足端坐标系与世界坐标系重合，且足端在髋关节全局坐标系下的坐标设为(Px，Py，Pz).

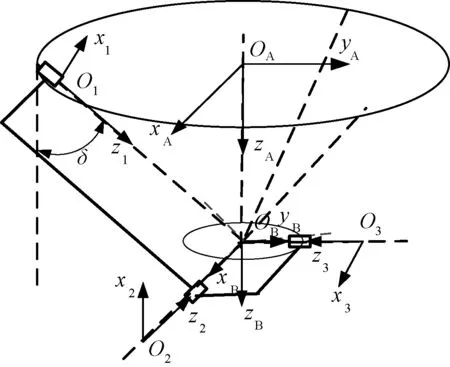
图4　髋关节坐标系Fig.4　Coordinate system of hip joint

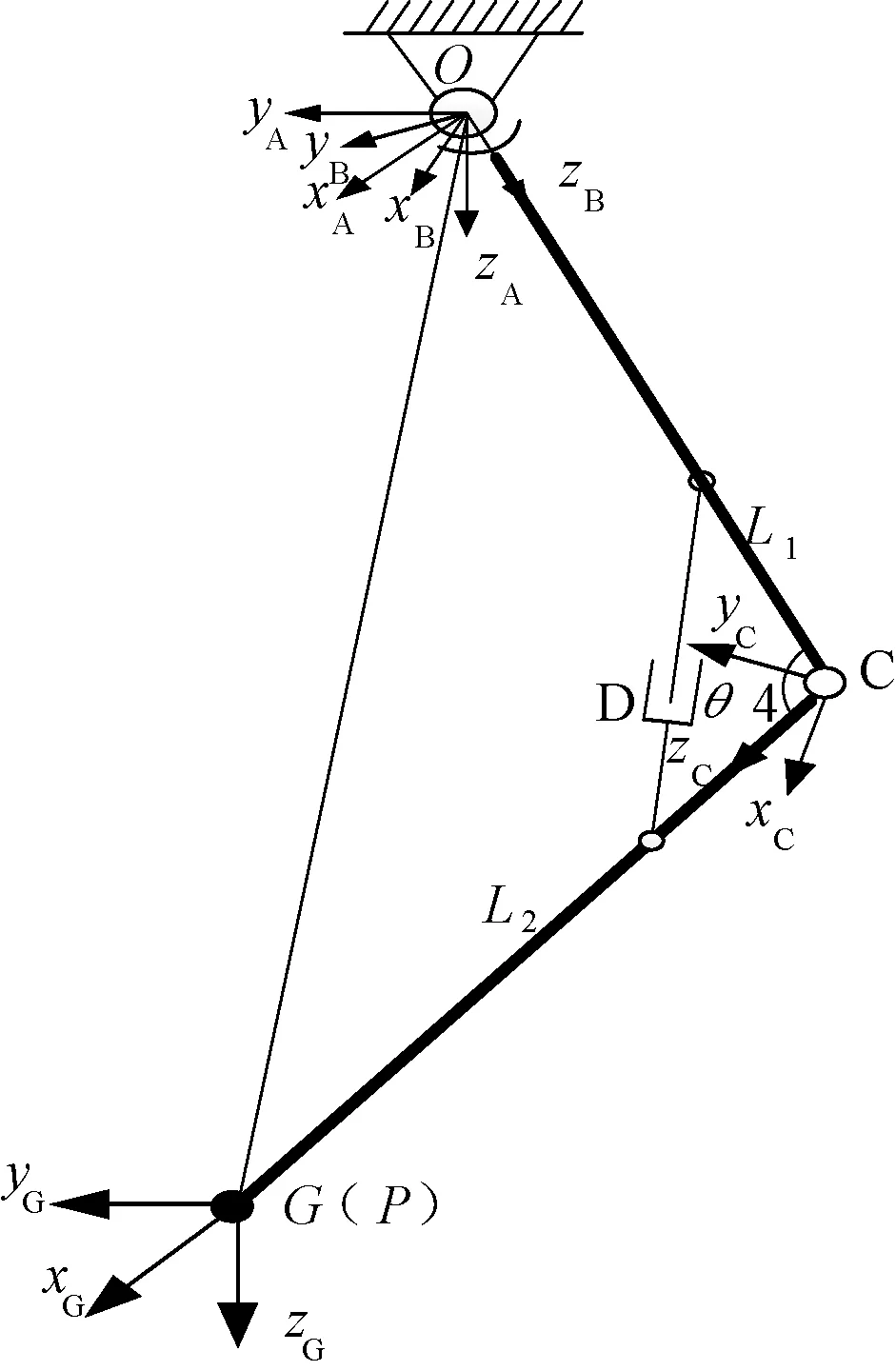
图5　腿部坐标系Fig.5　Leg coordinate system

根据文献[14]得到的串并混联腿的4个驱动表示为：

(1)

其中,

(2)

式中：α、β、γ为动平台相对于定平台按x-y-z顺序的RPY角，且其中(α,β,γ)满足

(3)

其中,

用D-H方法建立坐标系,描述全局坐标系下足端的表示，则

(4)

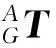
3　串并混联腿的轨迹规划

在四足步行机器人的步态行走中，伴随着支撑相和摆动相的交替进行，同时伴随着躯干的起伏变化[15].单腿足端从着地到再次离地腿部的连续相位变化过程称为支撑相，单腿的足端从抬腿离地开始沿规划轨迹运动到再次落地期间连续的相位变化过程称为摆动相.支撑相承载着机器人的负载并通过腿的相位变化移动机器人的躯干，完成目标方向的移动，其相位由步态的前极限相摆至后极限相；摆动相则由后极限相摆动至前极限相，摆动相决定着机器人的步幅大小和跨越障碍物时的抬腿高度[11].因此,单腿的轨迹规划包含摆动相和支撑相两个方面的轨迹规划.

3.1　摆动相零冲击轨迹规划

摆动相足端轨迹规划是机器人能够完成步态行走的重要环节.摆动相的运动可以分解成水平运动和竖直运动.笔者基于足端的零冲击思想结合高次多项式规划机器人的足端轨迹，所以在yG方向(水平方向)时让其轨迹满足式(5),

(5)

上述条件保证运动方向的轨迹在t=0和t=Tm时的速度和加速度都等于零，并且足端坐标分别是-S/2和S/2,其中S为摆动相足端的步幅，Tm为摆动相的周期.据此可以把yG方向的轨迹函数设为五次多项式

y=At5+Bt4+Ct3+Dt2+Et+F.

(6)

把式(6)带入式(5)计算得出的位移曲线为

(7)

同理摆动腿在zG方向(竖直方向)上先抬起然后落下，所以在设计时让其轨迹满足式(8),

(8)

式(8)保证了摆动腿在抬腿过程中，足端在t=0和t=Tm时速度和加速度为零，并限制了t=0、t=Tm/2、t=Tm时足端的位置分别是0、H、0，其中，H为抬腿高度.

故可以设zG方向的轨迹曲线为：

z=At6+Bt5+Ct4+Dt3+Et2+Ft+G.

(9)

把式(9)代入式(8)可以求得位移曲线：

(10)

令S=90 mm，H=20 mm，Tm=0.5 s，在摆动腿运动的一个周期内，用MATLAB可以计算出足端在yoz平面内的足端轨迹曲线,如图6所示.

图6　摆动相在yoz平面的足端轨迹Fig.6　The trajectory of the phase in the yoz plane

3.2　支撑相轨迹规划

支撑相是单腿的足端从着地到再次离地期间腿部的连续相位变化过程.它承载着机器人的负载并通过腿部的相位变化来移动机器人的躯干，从而完成目标移动.在规划支撑相时，假设机器人运动过程中腿部足端和地面之间没有相对滑动，躯干始终和地面保持平行，在支撑相时，支撑腿运动推动机体水平向前运动，等效于足端的轨迹水平向后移动.足端采用匀速直线运动，以减少在运动过程中足端与地面产生相对滑动.在此基础上进行足端轨迹规划，并利用反解模型求解支撑腿电机的驱动函数.

3.3　电机驱动函数

单腿周期是单腿完成摆动相和支撑相的时间.并且支撑相和摆动相的时间都是0.5 s.轨迹即是单腿的摆动相和支撑相轨迹的顺序执行.前面已经规划了单腿两个相位的足端轨迹，通过它的运动学反解[14]可以计算出各电机的驱动函数.在单腿机构的髋关节坐标系下，图7为膝关节电缸在一个周期内的变化量，图8为髋关节3个电机随时间的转角变化.从图7和8中可以看出，在一个完整的周期内，由机器人单腿运动学反解得到的电机转角的变化是连续的，说明根据多项式曲线规划的零冲击轨迹规划方案是可行的.

图7　膝关节电缸在一个周期内的位移变化Fig.7　Displacement of the knee joint in one cycle

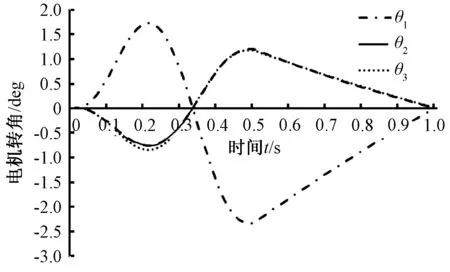
图8　髋关节3个电机在一个周期内转角变化Fig.8　Changes of three motors in the hip joint in one cycle

4　仿真试验

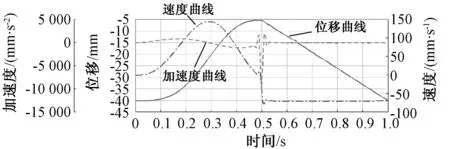
图9　足端点在x方向的位移、速度、加速度随时间变化图Fig.9　The displacement, velocity and acceleration of the foot end point in the x direction

图10　足端点在y方向的位移、速度、加速度随时间变化图Fig.10　The displacement, velocity and acceleration of the foot end point in the y direction

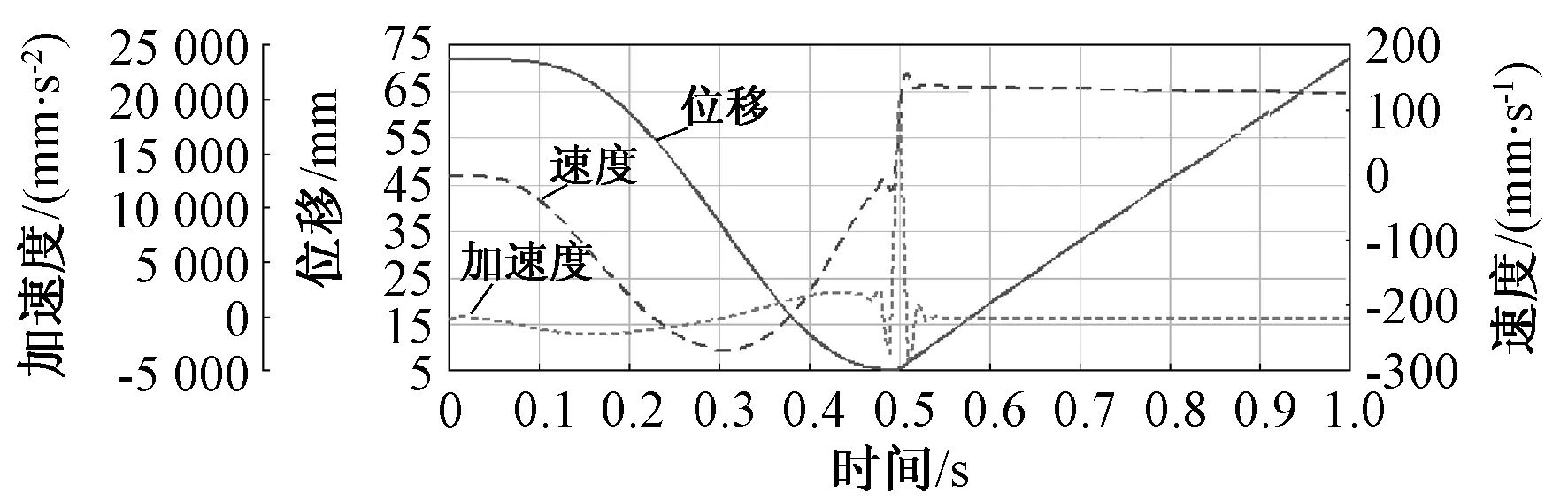
图11　足端点在z方向的位移、速度、加速度随时间变化图Fig.11　The displacement, velocity and acceleration of the foot end point in the z direction

将串并混联腿的solidworks模型另存为parasolid格式，然后导入ADAMS中，添加各构件的质量、约束和电机驱动以后，进行ADAMS仿真.由于在仿真时足端相对于动平台坐标系绕竖直方式旋转了30°，所以仿真结果在x、y、z方向上都有位移、速度、加速度的变化.在驱动函数的作用下，图9～11分别表示了足端一个周期内在x、y、z方向的位移、速度、加速度随时间的变化.在摆动相时，足端的速度、加速度都是连续的，并且大小与规划的一致，支撑相时做匀速直线运动.仿真的结果与足端轨迹规划的结果一致.但是摆动相与支撑相衔接的地方有较大的冲击，所以后续整机步态规划时考虑文献[11]提出的以短周期的正弦加速度加以引导，实现从零速到匀速和匀速到零速的平滑过渡，减小支撑相和摆动相间突然加减速造成的冲击.

5　结论

提出了一种新型串并混联的四足步行机器人，该机器人的每条腿部机构均是由髋关节和膝关节组成，具有4个自由度，髋关节是3-RRR并联机构，与膝关节组成串并混联机构.对其在运动过程中出现的冲击问题，使用了一种基于高次多项式的足端零冲击轨迹规划算法.利用D-H方法建立坐标系，在世界坐标系下对串并混联腿进行了基于高次多项式的零冲击足端轨迹规划.结合单腿运动学反解求出混联腿的4个驱动函数.之后通过ADAMS进行运动仿真分析，仿真的结果显示：串并混联腿能够满足规划的动作要求，轨迹的速度和加速度平滑，实现了零冲击的要求.证明了高次多项式曲线的零冲击足端轨迹规划算法的正确性和可行性，为后续整机的步态规划和运动控制奠定基础.

参考文献：

[1]谭民，王硕. 机器人技术研究进展[J]. 自动化学报，2013，39(7):963-972.

[2]王东署，朱训林. 未知环境中考虑姿态稳定性的自主机器人路径规划[J]. 郑州大学学报(工学版)，2014，35(5):31-35.

[3]SEMINI C, TSAGARAKIS N G, GUGLIELMINO E, et al. Design of HyQ-A hydraulically and electrically actuated quadruped robot[J]. Proceedings of the institution of mechanical engineers, part I: journal of systems and control engineering, 2011, 255(6): 831-849.

[4]YANG P, FENG G. A new six-parallel-legged walking robot for drilling hols on the fuselage[J]. Proceedings of the institution of mechanical engineerspart C: journal of mechanical engineering science, 2014,228(4):753-764.

[5]王洪波，齐政彦，胡正伟，等. 并联腿机构在四足/两足可重组步行机器人中的应用[J]. 机械工程学报，2009, 45(8): 24-30.

[6]田兴华，高峰，陈先宝，等. 四足仿生机器人混联腿构型设计及比较[J]. 机械工程学报，2013, 49(6): 81-88.

[7]李华. 内膝肘式四足机器人步态仿真[D]. 济南: 山东大学机械工程学院，2012.

[8]马东兴. 四足机器人步态规划与仿真[D]. 南京: 南京航空航天大学机电学院，2008.

[9]YOSHIHLRO S, KAZUTOSHI K, YUUJI H, et al. Foot trajectory for a quadruped walking machine [C]∥IEEE International Workshop on Intelligent Robots and Systems, IROS,1990, vol.1: 315-322.

[10] 柳洪义,宋伟刚，彭兆行. 控制步行机足运动的一种方法——修正组合摆线法[J]. 机器人, 1994, 16(6):350-356.

[11] 王立鹏，王军政，汪首坤，等. 基于足端轨迹规划算法的液压四足机器人步态控制策略[J].机械工程学报，2013，49(1)：39-44.

[12] 荣学文. SCalf液压驱动四足机器人的机构设计与运动分析[D]. 济南：山东大学控制科学与工程学院，2013.

[13] 程品，罗欣，顾瀚戈. 四足机器人砂砾地面对角行走控制方法[J]. 装备制造技术，2014(4):8-12.

[14] 高建设，李明祥，侯伯杰，等. 新型四足步行机器人串并混联腿的运动学分析[J].光学精密工程, 2015, 23(11): 3147-3160.

[15] 张秀丽. 四足机器人节律运动及环境适应性的生物控制研究[D].北京：清华大学精密仪器与机械学，2004.