VTI岩石界面产生的非均匀折射P波极化状态分析

法　林　张晓琳　席冰洁　周　鑫　牟锦鹏　杨　宏

(①西安邮电大学电子工程学院，陕西西安 710121； ②西安邮电大学通信与信息工程学院，陕西西安 710121)

1　引言

弹性各向异性在地球内部是一种常见的现象，许多地球物理学家已观察到各向异性介质中的极化现象[1-4]并对反射/折射系数、极化等方面进行了广泛的研究[5-11]，其研究成果已应用到勘探地震数据的反演解释中[12-15]。人们通常把沉积岩(例如页岩)视为横向各向同性(TI)介质，理论上VTI介质力学性质可用六角晶体的弹性张量进行描述[3，4]。

在地球物理勘探中，岩石的各向异性对声波的极化、传播和反射/折射有很大影响，正确地评估岩石各向异性的这些影响对地球物理勘探的正演建模和地震勘探数据反演至关重要。在许多已发表的文献中，可见各向异性岩层中传播的均匀平面波的极化特性方面的研究[1，4，16-19]，以及在各向异性岩层界面上产生的非均匀折射P波的极化特性方面的研究，例如，对于存在和不存在异常入射角的两种情况，法林等[10，20]推导了非均匀折射P波极化系数的严格数学表达式。

对于存在异常入射角的VTI介质界面的情况，在异常入射角对非均匀折射P波椭圆极化状态的影响下能够正确地计算出反射/折射系数的幅度及其相位与入射角之间的变化关系。如果忽略异常入射角引起的非均匀折射P波对极化状态的影响，则不能正确地在过异常入射角区域计算出VTI岩石界面的PP波的反射系数以及反射P波相对入射P波在界面上产生的渡越时间。因而对于大角度入射而获得的地震勘探数据就不能进行精确的AVO反演分析，对上述地震勘探数据进行时—深转换时也会引起较大的误差。

本文对各向异性岩石界面上产生的非均匀折射P波的极化状态进行了数值计算，用类似“Poincaré球”的可视化方式描述了岩石各向异性和异常入射角对其椭圆极化状态的影响。在VTI介质界面的反射系数和极化系数及前异常入射角区域非均匀模式转换波的极化系数表达式的基础上，推导了过异常入射角区域对应的非均匀模式转换波的极化系数的表达式，并首次建立了相应的椭圆极化方程，同时计算了入射角与椭圆极化轨迹之间的关系，并论证了这个异常入射角[10]不仅可以使椭圆极化轨迹的形状发生突变，而且还会使椭圆极化旋转方向发生改变。

2　理论背景

对于VTI介质，可以用六角晶系固体的弹性刚度张量

(1)

描述其主要力学性质[4，21]。式中Cij与各向异性岩石参数之间的关系[22]为

(2)

式中：ε、δ和γ是岩石各向异性参数；α和β分别是P波和SV波的垂直相速度；ρ是介质密度。

对于角频率为ω的简谐P波，其在x-z平面上传播并入射到VTI介质界面上(图1)，入射P波、反射P波、折射P波、反射SV波和折射SV波的质点位移矢量的表达式为

(3)

式中：θ为入射角、反射角或折射角；R0定义为1，R表示反射或折射系数；ux和uz为极化系数；k为波数。

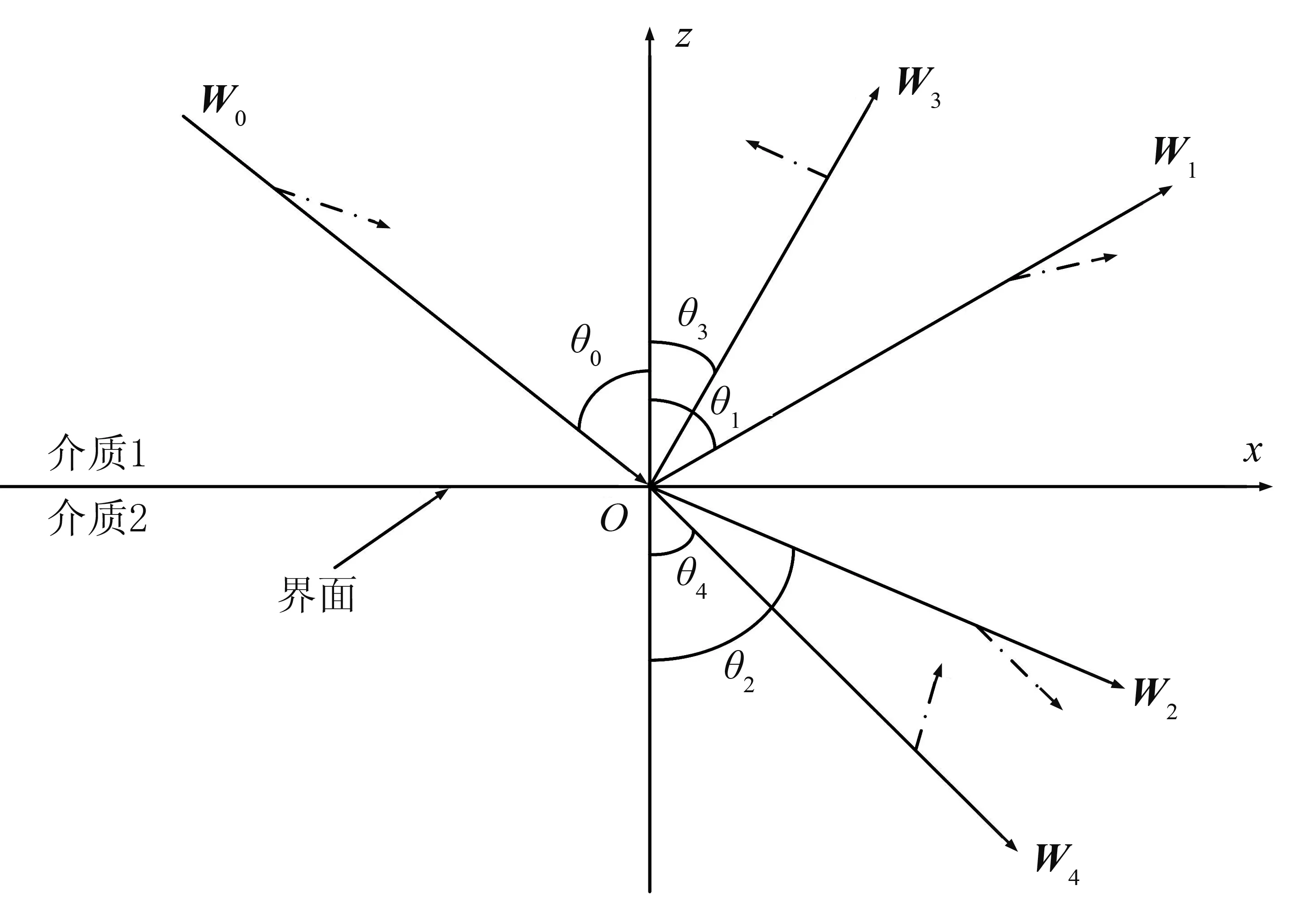
图1　　　　各向异性岩石界面模型的入射P波和模

对于不存在外力的情况，入射P波和在界面上产生的模式转换波的极化系数ux和uz可以通过求解简化的Christoffel方程

(4)

获得。式中

(5)

其中：A1=A11-A44；A2=A44-A33；A3=A13+A44；vm是五种波的相速度解[20]。在不存在异常入射角的情况下，对于入射、反射和折射P波式(5)中Qm取“+”，对于反射、折射SV波Qm取“-”；在存在异常入射角的情况下，在过异常入射角区域，对于折射P波Qm取“-”。

3　模型建立

根据测量出的岩石各向异性参数[22-24]，经大量计算后发现对于大多数各向异性岩石构成的界面不存在异常入射角，而对某些特殊各向异性岩石界面存在着异常入射角的现象[10]。选择各向异性页岩(A页岩)、泰勒砂岩(T砂岩)以及油页岩(O页岩)构成两种各向异性岩石界面模型：以A页岩作为入射介质、T砂岩作为折射介质，构成第一种各向异性岩石界面模型；以A页岩作为入射介质、O页岩为折射介质，构成第二种各向异性岩石界面模型。三种岩石的弹性参数如表1所示[22]。

表1　三种VTI介质岩石的弹性参数

3.1　模型1：不存在异常入射角情况

考虑不存在异常入射角的各向异性岩石界面系统，重点是对应折射P波的过临界角入射。由于岩石介质横向各向同性，有Wx,2=Wy,2，则模型可简化为二维。由斯奈尔定理，当sinθ2变为大于1的实数时，式(3)可以转换为质点位移分量表达式形式，即折射波质点位移的两个独立分量可表示为

(6)

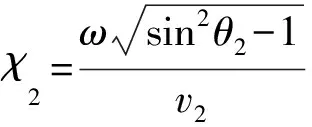
(7)

瞬时质点位移的表达式为

(8)

由上式可得非均匀折射P波的椭圆极化方程为

(9)

式中

(10)

其中上标“*”表示复共轭。将椭圆极化轨迹末端与x轴之间的夹角称为非均匀折射P波的椭圆极化旋转角，可表示为

tan(ωt-k0xsinθ0+φ2)]

(11)

上式表明椭圆极化旋转角随着时间的增大而增大，因此非均匀折射P波是右旋椭圆极化波。

对于给定的各向异性岩石界面，可以得到非均匀折射P波的椭圆极化轨迹与入射角之间的关系。对于A页岩和T砂岩组成的界面模型，不存在对应折射P波的异常入射角，仅存在一个对应折射P波的入射临界角(θ0C=48.34°)。在超过临界角区域，非均匀折射P波是右旋椭圆极化波，计算的非均匀折射P波的椭圆极化状态如图2a所示，可以看出，椭圆极化轨迹的大小相对于入射角的增大而减小；图2b为不同入射角的椭圆极化轨迹在Wx,2-Wz,2平面的投影；图2c是椭圆极化初始旋转角与入射角的关系，其绝对值随着入射角的增大而单调递增，当入射角接近90°时初始旋转角趋近于-90°。

3.2　模型2：存在异常入射角情况

对于A页岩作为入射介质、O页岩作为折射介质构成界面模型2，存在一个入射临界角(θ0C=32.99°)和一个异常入射角(θ0A=62.16°)。在前入射角区域，即θ0∈(θ0C，θ0A)，非均匀折射P波的椭圆极化状态的理论分析同模型1，非均匀折射P波的极化状态数学表达式相同，是一个右旋椭圆极化波。

在过异常入射角区域θ0∈(θ0A，90°)，由斯奈尔定理可知，当cosθ2变为大于1的实数时，式(3)可以转换为质点位移分量表达式形式，即非均匀折射P波质点位移的两个独立分量可以表示为

(12)

即

(13)

式中因子χ2=iωcosθ2/v2是正数[12，13]。由上式可得折射P波的椭圆极化方程

(14)

其中

(15)

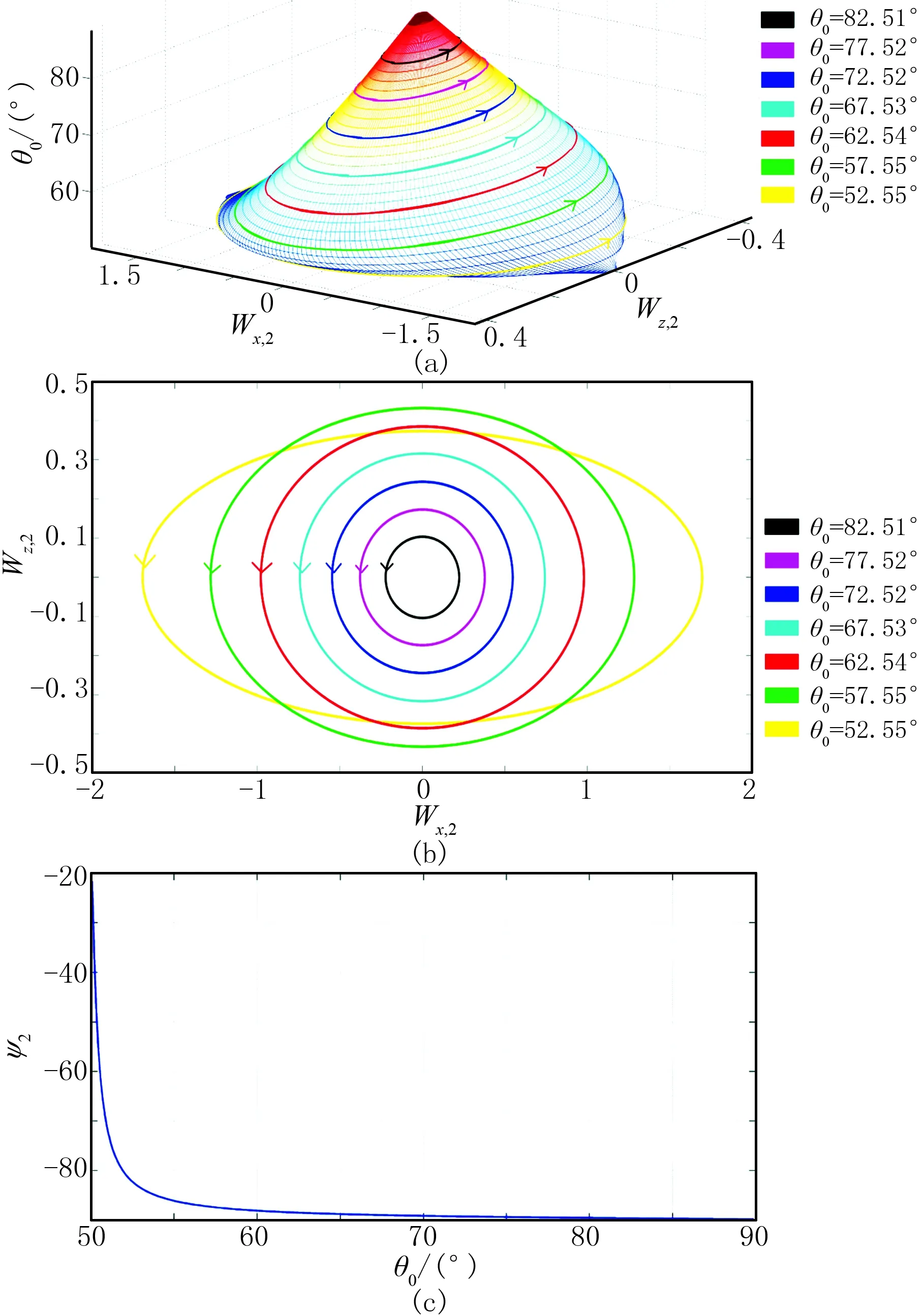
图2　界面模型1的非均匀折射P波的极化状态

(a)折射P波的椭圆极化轨迹与入射角的关系； (b)椭圆极化轨迹投影到Wx,2-Wz,2平面上； (c)在坐标原点处的椭圆极化的初始旋转角

同理，非均匀折射P波的椭圆极化旋转角可表示为

×

cot(ωt-k0xsinθ0+φ2)}

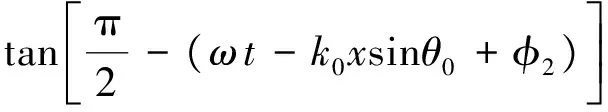
(16)

由上式可知，椭圆极化旋转角随着时间增加而减小，椭圆极化轨迹随着时间沿顺时针方向旋转，因此当θ0∈(θ0A，90°)，非均匀折射P波是左旋椭圆极化波。

图3为界面模型2的非均匀折射P波的椭圆极化状态。从图3a可以看出，椭圆极化轨迹的大小随入射角增加而减小，在异常入射角处，非均匀折射P波的椭圆极化轨迹突然增大，在过异常入射角区域θ0∈(θ0A，90°)，极化轨迹也是随着入射角的增大而

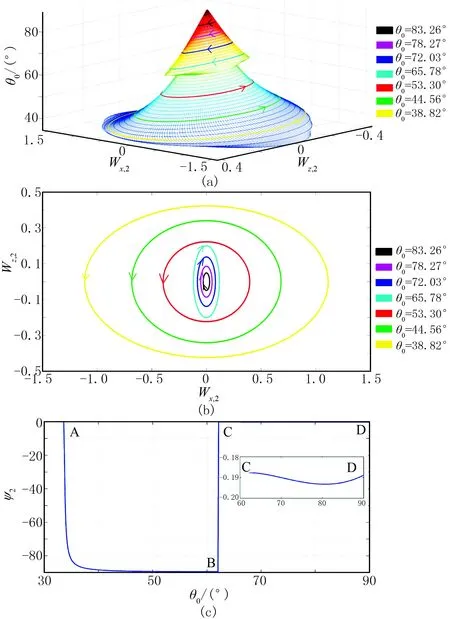
图3　界面模型2的非均匀折射P波的极化状态

(a)椭圆极化轨迹的左旋偏振和右旋偏振； (b)椭圆极化轨迹投影到Wx,2-Wz,2平面上； (c)在坐标原点处的椭圆极化旋转的初始状态减小。图3b为不同入射角得到的椭圆极化轨迹在Wx,2-Wz,2平面上的投影，可以看出，在小于异常入射角区域非均匀折射P波为左旋椭圆极化波，在大于异常入射角区域非均匀折射P波为右旋椭圆极化波。从图3c可以看出，非均匀折射P波的椭圆极化旋转初始角(绝对值)随入射角的增大而增大，当入射角向异常入射角的方向增大时，椭圆极化旋转初始角接近-90°； 在异常入射角处，椭圆极化旋转初始角(绝对值)突然减小，其旋转方向发生改变；在过异常入射角区域θ0∈(θ0A，90°)，椭圆极化旋转初始角相对较小，且变化较为缓慢(图3c中线段CD)。

4　结束语

基于两种真实的VTI介质界面模型，即A页岩与T砂岩之间界面以及A页岩与O页岩之间界面，本文推导了两种界面模型的非均匀折射P波的椭圆极化方程，分析了在上述两种界面上产生的非均匀折射P波的极化状态。在此基础上，给出了上述两种界面产生的非均匀折射P波的三维椭圆极化状态图(Poincaré球)。对于上述两种界面模型，其椭圆极化轨迹随着入射角的增大而减小。

对于存在异常入射角的VTI介质界面(界面模型2)，在异常入射角处，非均匀折射P波椭圆极化不但经历了形状突变、轨迹锐增和椭圆极化旋转初相角锐减的变化过程，而且由右旋椭圆极化波突变为左旋椭圆极化波。

[1]Crampin S，Stephen R A，McGonigle R.The polarization of P waves in anisotropic media.Geophysical Journal International，1982，68(2)：477-485.

[2]Tsvankin I D，Chesnokov E M.Synthetic of body waves seismograms from point sources in anisotropic media.Journal of Geophysical Research:Solid Earth，1990，95(B7)：11317-11331.

[4]Carcione J M.Wave Fields in Real Media：Wave Pro-pagation in Anisotropic，Anelastic and Porous Media.Elsevier,Amsterdam，2007.

[5]Fa L，Castagna J P，Dong H.An accurately fast algorithm of calculating reflection/transmission coefficients.Science China Physics Mechanics & Astronomy，2008，51(7)：823-846.

[6]Fa L，Castagna J P，Zeng Z et al.Effects of anisotropy on time-depth relation in transversely isotropic me-dium with a vertical axis of symmetry.China Science Bulletin，2010，55(21)：2243-2251.

[7]Fa L，Zhao M，Liu Y et al.Polarization of plane wave propagating inside elastic hexagonal crystal solids.Science China Physics Mechanics & Astronomy，2014，57(2)：251-262.

[8]徐文才，杨国权，李振春等.横向各向同性介质拟声波一阶速度—应力方程.石油地球物理勘探，2016，51(1)：87-96.

Xu Wencai,Yang Guoquan,Li Zhenchun et al.First order velocity-stress equation in TI media.OGP,2016,51(1):87-96.

[9]Fa L，Zhao J，Han Y et al.The influence of rock anisotropy on elliptical-polarization state of inhomogenously refracted P-wave.Science China Physics Mechanics & Astronomy，2016，59(4)：263-272.

[10]法林，聂琳，成洪申.用经典定理证明各向异性岩石界面异常入射角的存在.石油地球物理勘探，2017，52(2)：248-252.

Fa Lin,Nie Lin,Cheng Hongshen.Existence of ano-malous incident-angle on anisotropy rock interface verified by classic laws.OGP,2017,52(2):248-252.

[11]张恒磊，胡哲，胡祥云等.基于反射波各向异性特征的保真去噪方法.石油地球物理勘探，2017，52(2)：233-241.

Zhang Henglei,Hu Zhe,Hu Xiangyun et al.Seismic fidelity de-noising with reflection anisotropy.OGP,2017,52(2):233-241.

[12]羊屋三维处理、解释一体化方法研究组.纵波VTI介质理论与应用研究.石油地球物理勘探，2002，37(3)：267-275.

Research Group for 3-D Processing and Interpretation Integrated Method.Research on P-wave theory in VTI media and its application.OGP,2002,37(3):267-275.

[13]羊屋三维处理、解释一体化方法研究组.VTI介质的AVO理论与应用研究.石油地球物理勘探，2002，37(4)：363-371.

Research Group of Method for Yangwu 3-D Integrating Processing into Interpretation.Study of AVO theory and its application in VTI medium.OGP,2002,37(4):363-371.

[14]刘瑞合，赵金玉，印兴耀等.VTI介质各向异性参数层析反演策略与应用.石油地球物理勘探，2017，52(3)：484-490.

Liu Ruihe,Zhao Jinyu,Yin Xingyao et al.Strategy of anisotropic parameter tomography inversion in VTI medium.OGP,2017,52(3):484-490.

[15]李勤，李庆春，张林.VTI介质多波各向异性参数分析.石油地球物理勘探，2014，49(3)：503-507.

Li Qin,Li Qingchun,Zhang Lin.Anisotropic parameter analysis of multi-component data in VTI media.OGP,2014,49(3):503-507.

[16]Hosten B.Reflection and transmission of acoustic plane waves on an immersed orthotropic and visco-elastic solid layer.Journal of the Acoustical Society of America，1991，89(6)：2745-2753.

[17]Lanceleur P，Ribeiro H，Belleval J D.The use of inhomogenous waves in the reflection-transmission problem at a plane interface between two anisotropic media.Journal of the Acoustical Society of America，1993，93(4)：1882-1892.

[18]Helbig K，Schoenberg M.Anomalous polarization of elastic waves in transversely isotropic media.Journal of the Acoustical Society of America，1987，81(5)：1235-1245.

[19]Daley P D，Hron F.Reflection and transmission coefficients for transversely isotropic media.Bulletin of the Seismological Society of America，1977，67(3)：661-675.

[20]Fa L，Brown R L，Castagna J P.Anomalous post-critical refraction behavior for certain transversely isotropic media.Journal of the Acoustical Society of America，2006，120(6)：3479-3492.

[21]Auld B A.Acoustic Fields and Waves in Solids.John Wiley and Sons，New York，1973，107-124.

[22]Thomsen L.Weak elastic anisotropy.Geophysics，1986，51(10)：1954-1966.

[23]Wang Z.Seismic anisotropy in sedimentary rocks，part 2：Laboratory data.Geophysics,2002,67(5)：1423-1440.

[24]Vernik L，Nur A.Ultrasonic velocity and anisotropy of hydrocarbon source rocks.Geophysics，1992，57(5)：727-735.