立体几何复习要点例析*

2018-04-04三山高级中学浙江慈溪315300慈溪市教育局教研室浙江慈溪315300

中学教研(数学) 2018年4期

关键词：平面角二面角三视图

●　　(三山高级中学，浙江慈溪　315300)　●　　(慈溪市教育局教研室，浙江慈溪　315300)

1　知识内容

《浙江考试》2018年第1期公布了“2018年浙江省普通高考考试说明(数学)”，明确2018年高考必考科目数学考试说明内容与2017年相同.关于立体几何与空间向量部分，建议关注以下内容与要求：

1)理解柱、锥、台、球的结构特征，会计算柱、锥、台、球的表面积和体积；

2)掌握三视图所表示的空间几何体，会用斜二测法画出它们的直观图；

3)理解空间点、直线、平面位置关系的定义，掌握4个公理、1个定理；

4)理解空间线面平行、线面垂直、面面平行、面面垂直的判定定理与性质定理；

5)理解直线与平面所成角的概念，了解二面角及其平面角的概念；

6)了解空间直角坐标系，会用空间直角坐标表示点的位置，了解空间距离、夹角公式、平面法向量、方向向量；

7)了解求两直线夹角、直线与平面所成角、二面角的向量求法．

2　命题分析

回顾近4年的浙江省数学高考试题，有关立体几何与空间向量的试题分布如下：

2014年考查了3道题共24分：其中一道选择题5分(考查三视图求表面积)、一道填空题4分(考查求线面角)、一道解答题15分(考查线面垂直和二面角的平面角)；

2015年考查了4道题共29分：其中两道选择题均为5分(分别考查三视图求体积、翻折问题和二面角的平面角)、一道填空题4分(考查线线角)、一道解答题15分(考查线面垂直和二面角的平面角)；

2016年考查了4道题共30分：其中一道选择题5分(考查位置关系)、两道填空题分别为6分(考查三视图求体积和表面积)和4分(考查四面体的体积最大值)、一道解答题15分(考查线面垂直和二面角的平面角)；

2017年考查了3道题共23分：其中两道选择题均为4分(分别考查三视图求体积、二面角的平面角大小比较)、一道解答题15分(考查线面平行和线面角)．

2018年预测会有3～4个试题，分值在25分左右：选择题、填空题主要涉及空间点、直线、平面位置关系的判断，结合三视图求体积、表面积(可结合数学文化)，简单的空间角计算(两直线夹角、直线与平面所成角、二面角的平面角)，翻折问题，动态轨迹问题；解答题主要考查在空间几何体(特别是组合体)中直线与平面、平面与平面的位置关系(平行和垂直)及空间角(主要是线面角)的计算．

3　典例剖析

考点1空间点、直线、平面位置关系的判断.

例11)设l为直线，α,β是两个不同的平面，下列命题中正确的是

()

A．若α⊥β，l∥α，则l⊥β

B．若l∥α，l∥β，则α∥β

C．若l⊥α，l∥β，则α∥β

D．若l⊥α，l⊥β，则α∥β

(浙江省湖州、衢州、丽水三地市2018年1月高三数学期末试题第3题)

2)已知α,β是两个不同的平面，直线l⊂α，则“l⊥β”是“α⊥β”的

()

A．充分不必要条件

B．必要不充分条件

C．充分必要条件

D．既不充分也不必要条件

(浙江省嵊州市2017学年第一学期高三数学期末试题第5题)

分析1)答案为D．选项A中l⊥β，l⊂β，l∥β,l与β斜交均有可能；选项B中α∥β，α与β相交均有可能；选项C中α∥β错误，应为α⊥β；选项D正确．也可以直接用结论“和同一直线垂直的两个不重合平面平行”得到．

评注空间点、直线、平面的位置关系考查是命题者比较关注的一个方向，往往以选择题形式出现，若干个命题组合进行真假判断或者结合充要条件考查，属于容易题，可以“证明结论正确”与“举反例否定(画草图排除)”相结合来解决.复习冲刺查漏补缺时要关注概念、定理的准确性，比如线面平行、线面垂直、面面平行、面面垂直的判定定理和性质定理，记忆要求清楚，特别是条件的增删，会影响结论的正确性．

考点2三视图与体积、表面积.

例21)《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，已知某“堑堵”的三视图如图1所示，俯视图中虚线平分矩形的面积，则该“堑堵”的侧面积为

()

(浙江省上虞市2017学年第一学期高三数学期末试题第5题)

图1　　　图2

2)某几何体的三视图如图2所示(单位：cm)，则该几何体的表面积(单位：cm2)是

()

(浙江省嘉兴市2017学年第一学期高三数学期末试题第6题)

分析1)根据题意，结合三视图可以判断该“堑堵”是直三棱柱(如图3)，△ABC的周长为

故选C.

图3　　　图4

2)根据三视图可以判断该几何体由上、下两部分组成(如图4)，其中上半部分为正方体，下半部分为正四棱台，正方体中5个面的面积之和为

S1=5×(2×2)=20,

正四棱台的下底面面积为S2=16 cm2，正四棱台的侧面积为

因此，该几何体的表面积为

故选B．

评注根据三视图求体积、表面积每年必考，以选择题或者填空题的形式考查，命题方向可以以数学文化、组合体为载体，或以棱柱、棱锥中的某一部分(几何体残缺)为载体，考查三视图的知识和几何体的体积、表面积计算，试题难度有容易也有中等，关键是能够对给出的三视图进行恰当的分析，从三视图中发现几何体中各元素间的位置关系及数量关系．对几何体残缺的还原，一般方法是从俯视图出发，结合正视图、侧视图来还原，特殊情况需构造正方体(或长方体)，使所求的几何体为正方体(或长方体)的一部分.教师在平时讲评三视图题目时，建议学生加强识图训练，多动手画画．

考点3简单的空间角计算.

例31)如图5，在三棱锥P-ABC中，PA⊥平面ABC，∠BAC=90°，D,E分别是BC,AB的中点，AB≠AC，且AC>AD．设PC与DE所成角为α，PD与平面ABC所成角为β，二面角P-BC-A为γ，则

()

A．α<β<γB．α<γ<β

C．β<α<γD.γ<β<α

(2017学年浙江省杭州市第一次高考科目教学质量检测数学试题第8题)

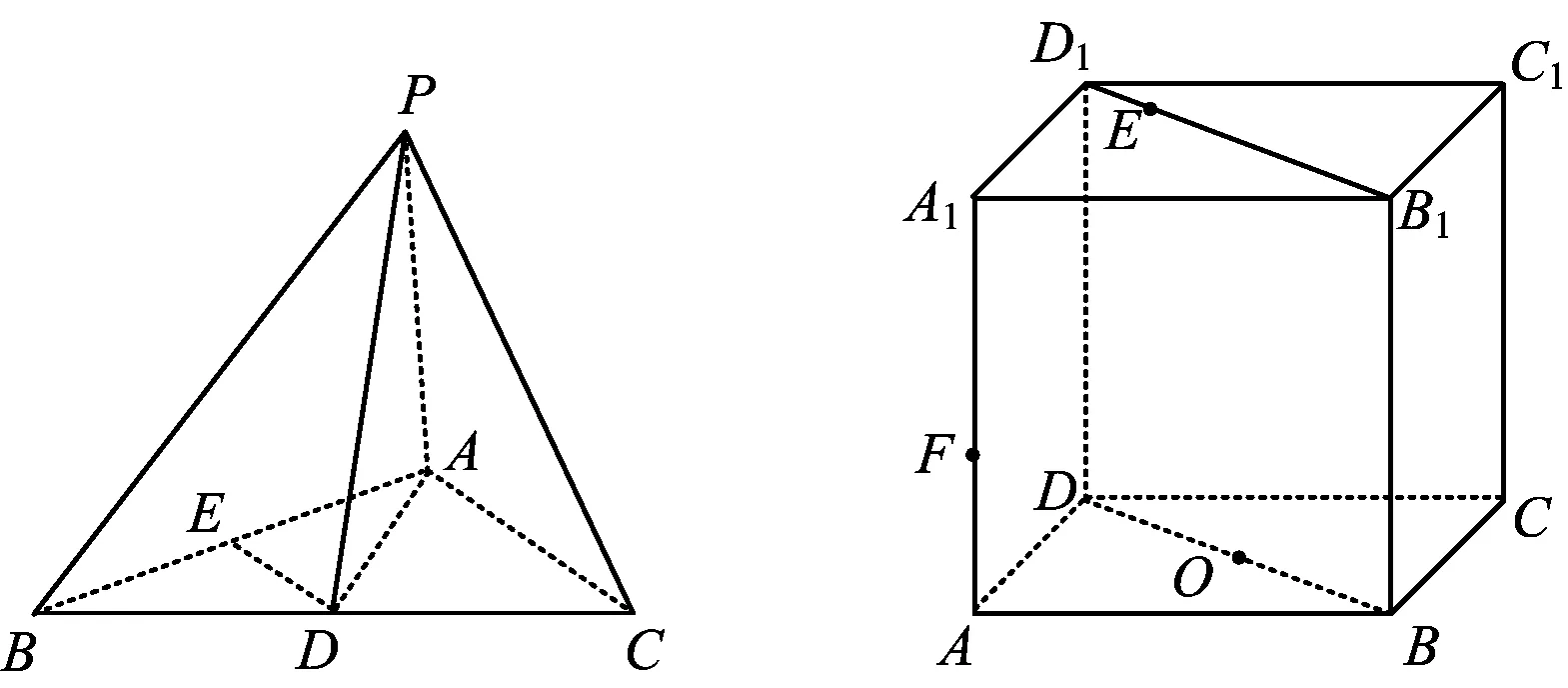
图5　　　图6

()

A．α>γ>βB．γ>β>α

C．γ>α>βD．β>α>γ

(金华十校2018届第一学期高三数学期末试题第9题)

即

tanγ>tanβ>tanα，

亦即

γ>β>α.

故选A.

2)如图7，记AC∩BD=O，A1C1∩B1D1=O1，联结OB1,OE，易知AC⊥平面BDD1B1.作FH⊥平面BDD1B1，则点H在OO1上；作HM⊥OB1于点M,联结FM；作HN⊥OE于点N,联结FN,易得

FM⊥OB1,FN⊥OE,FO1⊥B1D1,

从而

∠FMH=α,∠FNH=β,∠FO1H=γ，

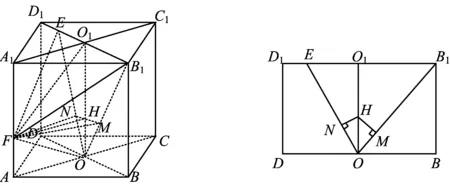
图7　　　图8

在图8中不难发现HN

即

tanβ>tanα>tanγ，

亦即

β>α>γ.

故选D.

评注立体几何中角的大小比较问题，有多种解法，常见的是直接法，即利用“作证算”，结合空间问题平面化的技巧，计算简单的空间角(两直线夹角、直线与平面所成角、二面角的平面角).第2)小题亦可以用极端思想简化问题，快捷、正确：当点F无限接近点A时，容易发现γ最小，直接排除选项A,B,C.

考点4动态问题.

(浙江省嘉兴市2017年3月高三年级教学质量检测数学试题第17题)

图9　　　图10

(浙江省台州市2017年高三年级第一次调考数学试题第17题)

分析1)如图11，取CD的中点H，联结AH，BH,易知∠AHB为二面角A-CD-B的平面角，于是

图11　　　图12

(1)

代入式(1)得到

即

故|L|表示周长，值为π.

评注动态的立体几何问题包括变量取值范围、轨迹、不变性、存在性等问题.解决此类问题需要灵活运用有关知识，建立一些数学模型，进行推理、论证及代数运算.可以从几何角度入手，也可以从建系入手，要善于挖掘问题所隐藏的数学模型，然后解决问题，如发现轨迹是圆、圆锥曲线、圆锥等，可以利用它们的性质进行解答.关注经典结论，如最小角定理(斜线与平面所成的角是斜线与平面内所有直线所成角中的最小角)应用.

考点5翻折问题.

例51)如图13，点E是正方形ABCD边CD上的一点(不包括端点)，将△DAE沿AE折起得到△D′AE，且平面D′AE与平面ABCE异面.记二面角D′-AE-B的平面角为α，CD′与平面ABC所成角为β,则在D′的运动过程中，使得|tanα|=2tanβ成立的不同β有

()

A．0个或1个B．1个或2个

C．0个或2个D．0个或1个或2个

(浙江省诸暨市2016学年第一学期高三数学期末试题第10题)

图13

(浙江省宁波市2017学年第一学期高三数学期末试题第17题)

图14　　　图15

当点P,M,Q共线且PQ⊥平面BGHC时,等号成立.故所求最小值为1．

评注翻折问题是将一个平面图形通过翻折变成空间几何体.平面图形在翻折过程中，抓住折叠过程中变与不变的几何量:某些几何量(长度、角度等)保持不变，或某些几何性质或位置关系(垂直关系等)不变，这些定值、定性问题是翻折前后立体几何中的重要问题.一般翻折后仍在同一平面内的相关几何量的位置及大小不变，在解决立体几何问题时仍然是将立体几何问题转化为平面几何问题，在限时应试中，我们要利用选择题、填空题的特点来解题，即“小题小做”.

考点6解答题中的证明与计算问题.

例6如图16，四棱锥S-ABCD中，AB∥CD，BC⊥CD，AB=2，BC=CD=SD=1，侧面SAB为等边三角形.

1)证明：AB⊥SD；

2)求直线SC与平面SAB所成角的正弦值.

(金华十校2018届第一学期高三期末调研数学试题第19题)

图16　　　图17

评注高考立体几何解答题一般分两个小题.过去分文理科的时候，关于空间角的计算，理科考查二面角的平面角，文科考查线面角;现在文理不分后，考查线面角的概率很高.建议立体几何解答题复习做好以下3点：1)在复习时空间几何体的类型要丰富，要多样化.2)第1)小题主要是平行与垂直的证明，对于平行问题尽量用传统法，对于垂直问题既可以用传统法，也可以转化为线线垂直后利用数量积为0.在答题书写时要特别突出平行和垂直的转化思想.3)对于第2)小题的解答用向量法比较熟练，但要注意合理的建系，写好关键点坐标，并与传统法的结合，加强分析从而达到减少计算、提高计算准确率的目的.