体验数学概念教学的生成过程*
——基于“指数函数及其性质”概念教学的反思与认识
2018-04-04杭州高级中学浙江杭州321008
● (杭州高级中学,浙江 杭州 321008)
最近在浙江省杭州市优质课评比中,笔者开设了一堂公开课“指数函数及其性质”.下面将笔者的想法、教学过程和反思分享给大家,供参考.
1 情景引入
情景1对折一张足够大的纸,对折一次,厚度变成原来的2倍,对折两次,厚度变成原来的4倍,对折3次,厚度变成原来的8倍,……,如果对折x次,厚度变成原来的y倍,如何描述这两个变量之间的关系?如果纸张的厚度为0.1 mm,对折30次,总厚度为多少?对折50次呢?
生1:y=2x(其中x∈N*).
师:我们检验一下,对任意x∈N*,是否都有唯一确定的y与之对应.
生(全体):是.
师:我们把x与y的对应关系叫做函数关系,x是自变量,y是函数值,定义域为N*.接下来,我们看第二个问题:对折30次,总厚度为多少?
生2:y=0.000 1×230=107 374.182 4 (m).
师:107 374.182 4>8 844.34.如果能折30次,那么纸的厚度将超过珠穆朗玛峰的高度,那折50次呢?
视频播放资料根据科学爱好者的说法:
对折3次=你指甲的厚度;
对折7次=128页的笔记本的厚度;
对折10次=一只手的宽度;
对折23次=1公里,大约3 280步;
……
对折30次=100公里,这样的厚度已经足够带你上天了;
对折42次=这样的厚度可以到达月球;
对折51次=这样的厚度可以拜访太阳;
对折81次=127 786光年,大概就是一个仙女座星系;
对折103次=930亿光年,大于已知宇宙的厚度.
师:这出乎我们的意料,令人震撼.因为x越大,函数值上升的速度越快,我们将这种上升速度,形象地称为“指数爆炸”.


师:很好,还有其他想法吗?
生4:其中x∈N*.
师:x是正整数吗?请问时间有没有1.5年、1.25年的说法?
生(全体):有.
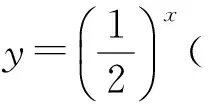
教学反思情景引入让学生体会数学来源于生活,大量的数学模型都是以生活实例为现实原形的.
本环节中有2个亮点:
1)情景1中的一段素材资料(教学时是一段视频),深深地吸引了学生,唤起了学生的学习热情和强烈的求知欲.
2)在设计上,情景1和情景2层层递进,定义域从N*到全体正数,将两个函数抽离实际背景,巧妙地把两个函数的定义域推广到R,起到了承上启下的作用.
2 概念建构
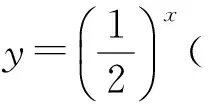
生5:都是指数幂形式.
生6:底数都是常数.
生7:自变量都在指数位置.
生8:定义域都为R.
师:很好!1)都是指数幂形式;2)自变量在指数位置;3)底数是常数;4)定义域为R.类似这样的函数,还能再举几个例子吗?
生9:y=6x,y=(0.6)x.
师:综合这些函数的共同点,能用一个统一的形式来表示吗?
生10:y=ax.
师:这是一般的函数模型,其中x是自变量,y是函数值,底数a不同就得到不同的函数.那么,若要满足x∈R,底数a的取值有什么要求呢?
生11:a≠1.
师:为什么?
生12:因为当a=1时,y=1是常数函数,不具备单调性.
师:还有什么要求呢?
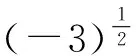
生14:a≠0,因为00没有意义.
师:大家分析得非常好.我们得到a的取值范围a>0且a≠1,此时,y=ax的定义域为R.
(教师PPT投影指数函数的概念:一般地,函数y=ax(其中a>0且a≠1)叫做指数函数,其中x是自变量,定义域为R.)
例1判断下列函数中哪些是指数函数?
1)y=(-2)x;2)y=2x+1;3)y=3·4x;
4)y=x4;5)y=0.3x;6)y=2x+1;
7)y=πx;8)y=xx.
教学反思概念建构就是告诉学生要从实际例子中抽象概括出指数函数模型,启发学生运用函数模型表述、思考和解决现实世界中蕴含的规律[1].
本环节中有2个亮点:
1)让学生归纳出一些具体函数的共同特征,再让学生举出一些类似函数,最后进行归纳概括得一般形式.让学生经历由部分到整体、由个别到一般的归纳推理过程.
2)学生能轻松自然地得到a>0且a≠1,得益于教师在情景引入中巧妙地将指数函数的定义域变成R..
3 性质探究
师:到此我们得到了一个新的函数模型,那么按照基本初等函数的研究思路,接下来我们要研究函数的什么性质呢?
生15:单调性、最大值、最小值、奇偶性等.
师:对,很好!这些就是我们要研究的函数性质,而我们通常根据什么载体去研究函数的性质呢?
生16:函数图像.
师:很好,画函数图像可用什么方法?
生17:描点法.
师:描点法的具体步骤是什么?
生18:列表、描点、连线.
师:研究基本初等函数性质的基本方法和步骤:形成函数定义→作出函数图像→研究函数性质→运用函数性质.
师:接下来我们用描点法画出指数函数的图像,但是画哪一个呢?画y=ax吗?
生19:y=ax的图像一下子画不出来,但可以画y=2x.

(学生开始动手列表画图,教师巡逻,然后将其中一位学生的作图情况进行投影,并在此强调画图需要列表、描点、连线等步骤.教师打开几何画板,直接演示画图,让学生直接面对面感受数形结合之美.)
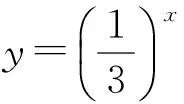
(学生画好后,教师再对学生所画的图像作出评价.)

图2
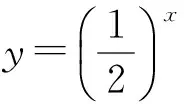
(教师用PPT演示,让学生感受列表、描点、连线的过程.)

生20:这两个函数图像关于y轴对称.
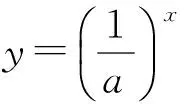


图2
生21:如图2,可以按照底数a分成两类:1)当a>1时,y=ax单调递增;2)当0 生22:它们的共同点是过点(0,1),并且始终在x轴上方. 生23:当a>1时,a越大,图像越靠近y轴;当0 师:把这些图像特征分别对应相应的函数性质,我们一起把函数性质表格填完(填表过程略). 教学反思1)教师虽然画出图像,并用函数图像来研究函数性质,但是因为设计的问题比较分散、零碎、封闭,没有形成问题串的形式,所以没能让学生从一个基础问题出发层层递进并展开讨论,教师上课过程就显得比较凌乱.如果把问题变成:请大家自己选择a的值,画几个具体函数的图像,然后分小组讨论图像有什么特征.用这样一个问题引领,显得开放,既有学生的独立思考,又有小组合作学习,从整体上把握函数研究的一般方法[2]. 2)这一环节可以很好地体现“从具体问题出发→观察、分析→归纳、类比→提出猜想→演绎证明”这个数学发现的一般过程.虽然教师努力想体现“从具体到抽象、从特殊到一般的归纳推理形式”,但仅由几个特殊函数图像得到函数性质,没有大量用几何画板演示当a在(1,+∞)和(0,1)两个范围内变化时的图像变化的一般情况及函数性质,不利于学生形成从特殊到一般的归纳推理模式[3]. 3)推理与证明是本节课需要重视的一个问题,这正是数学有别于其他学科的显著特点,数学结论的正确性必须通过逻辑推理的形式加以证明.但本环节仅由几个具体函数的图像归纳出相关结论,并未对结论给出证明或者说明. 巩固应用就是内化新知,深化对指数函数的理解,极大地提高了学生灵活运用图像和性质的能力. 师:指数函数及其性质可以应用在哪里呢? 图3 例2已知指数函数f(x)=ax(其中a>0,且a≠1)的图像经过点(3,π),求f(0),f(1),f(2). (教师投影一位学生的解题情况,并在此强调解题的规范.) 师:由题意得f(1)=a,说明函数y=ax图像也经过点(1,a),这不仅可以帮我们结合(0,1)简单画出指数函数y=ax的图像,还可以解释a越大,图像越向上升(如图3). 例3比较下列各题中两个值的大小: 1) 1.72.5与1.73;2) 0.8-0.1与0.8-0.2; (教师投影一位学生的解题情况,并在此强调解题归纳和总结.) 师:总结比较大小的方法:1)当底数相同且明确底数a与1的大小关系时,直接用函数的单调性来解;2)当底数相同但不明确底数a与1的大小关系时,要分情况讨论;3)当底数不同时,可以转化成同底数或借助中间值来比较两个数的大小. 例4解下列关于x的不等式: 1)3x≥30.5;2)0.2x<25;3)ax2-2x≥a3. 这是挑战题,对学生来说有点难度,教师可从思想、方法上加以提升和总结. 教学反思本课是指数函数第一课,教学重点应在指数函数模型的建构及其性质探究,不宜花过多时间用于例题讲解,例题不能选得太难,不可以把概念课上成习题课. 师:本节课我们从知识点、数学思想、数学方法等方面学会了什么? 教学反思教师能够从知识、思想方法层面加以小结,非常好,但最好加上学生的情感体验,如:你体验到了什么,感悟到了什么,等. 以上是笔者参加这次优质课比赛的一点感悟,在上课时笔者也注意到需对学生的回答及时肯定,以及规范自己的板书.重新回顾教学过程,并及时查找教科书及教学参考书,对概念课有了更深层次的理解,以下是笔者对概念课教学的一点体会: 1)结合一节课的重点和难点,以及教师对教材的分析,设计问题串,用问题驱动教学,将教师的三维目标融入教学过程中. 2)仔细推敲数学概念中每个字的含义,如指数函数的定义域为R,为什么底数a有a>0且a≠1的要求.通过对概念的探索,加强学生对概念的理解和记忆. 3)《新课程标准》强调学生对知识的探求和发现的过程,不再像传统教学那样注重教师的教,因此教师要教会学生发现新知的方法.在教学过程中,教师设计生活情景,用一些具体函数的图像特征和性质归纳推理出一般结论,最后证明这些结论.让学生在探索中寻找乐趣,学会用数学方法解决实际问题. 5)一定要注意数学符号的正确使用与转化.概念的文字叙述、符号表示、图形表示要转化到位,如本节课中先是概括出指数函数的文字概念,进一步形成符号表示y=ax(其中x∈R),最后画出图像进行性质研究. 概念课的重要功能就是可以让学生学会从数学角度看生活中的各种问题,培养学生的数学思想,并用数学知识解决生活中的实际问题,体现数学的生活美及抽象美[4]. [1]马茂年.快乐教学改善心育领悟本 质——从“教书匠”走向“名教师”[J].中学教研(数学),2013(7):4-7. [2]周仕荣.数学课堂规范的讨论和分析[J].数学教育学报,2012,21(1):80-81. [3]王光明,刁颖.高效数学学习的心理特征研究[J].数学教育学报,2009,18(5):51-56. [4]马茂年,俞昕.课堂教学回归“数学化”的讨论和分析——以高中“数学归纳法”的教学为例[J].数学教育学报,2013,22(6):83-84.4 巩固应用

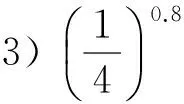

5 归纳小结