高速流场中变刚度复合材料层合板颤振分析

欧阳小穗，刘毅

同济大学 航空航天与力学学院，上海 200092

壁板颤振研究始于20世纪50年代。Miles[1]和Jordan[2]最先对壁板颤振进行了理论分析。Olson[3-4]最早用有限元法研究壁板颤振问题，分析了超声速流中二维壁板的颤振边界。Kouchakzadeh等[5]研究了高速流场中复合材料层合板非线性气动弹性问题，分析了面内载荷、静压差、纤维方向和气动阻尼对壁板非线性气动弹性特性的影响。结果表明，纤维方向对板的动力学特性有明显影响，板的非对称特性改变了极限环振动性能。Abdel-Motaglay 等[6]针对任意方向来流对复合材料板大振幅超声速颤振的影响提出了一种有限元公式，并对偏航超声速流中各向同性和正交各向异性复合材料板进行了分析。Singha和Ganapathi[7]采用剪切变形有限元法研究了系统参数对复合材料层合板的超声速颤振特性的影响。估算了临界动压随板的倾斜角、纤维方向和边界条件的变化；分析了气动力、结构阻尼以及热载荷对临界动压的影响。国内学者在复合材料壁板颤振方面也进行了系统深入的研究。王晓庆等[8]采用4节点24自由度板单元研究不同温度场的偏航壁板颤振问题，进行了考虑偏航壁板颤振速度和壁板重量的多目标热颤振优化设计，得到偏航壁板颤振随温升出现“跳跃”现象的结论。苑凯华和邱志平[9-10]采用有限元法研究了高速流场中复合材料壁板热颤振问题，考虑结构参数不确定性对壁板颤振的影响，提出用区间描述不确定性因素估计壁板颤振临界风速近似区间，以及发生极限环振动时的振幅变化区间，数值算例验证了方法的有效性和可行性。杨智春等[11]采用分步求解方法研究了复合材料壁板的热颤振，得到3种不同铺层复合材料壁板颤振临界速度和温升间的关系。高扬等[12]应用有限元法研究气流偏角和热载荷对不同形状复合材料壁板颤振特性的影响，分析了不同形状复合材料壁板颤振临界动压随温升和气流偏角的变化规律。吕秀秀等[13]研究超声速流场中铺层方式和铺层方位角对复合材料层合板颤振特性的影响。

传统的纤维增强复合材料层合板采用的是直线纤维(如图1(a)所示)，也就是说纤维方向在单层内是不变的；随着自动铺放等先进制造技术的发展，利用自动铺放设备能够改变铺层的纤维方向,使得纤维方向在铺层内曲线变化(如图1(b)所示)[14]。不同于传统的直线纤维复合材料单层板，曲线纤维复合材料单层板中每一点的纤维方向都是不同的，随位置变化而连续变化，单层内不同位置处的刚度也随纤维方向的变化而变化，呈现出变刚度的特点。这种含曲线纤维铺层的复合材料称为变刚度复合材料。变刚度复合材料在减轻结构重量和降低制造成本等方面已显示出优势。

曲线纤维复合材料最早由Hyer等[15-16]提出用来代替直线纤维以提高带孔复合材料层合板的力学性能。随后，Gürdal等[17-20]提出了变刚度复合材料概念，研究中考虑固化过程产生的残余热应力等因素，结果表明，曲线纤维复合材料层合板与传统的直线纤维复合材料相比，屈曲性能有较大提高。Wu等[21-22]采用数值方法对曲线纤维复合材料的屈曲和后屈曲性能进行了研究。杜宇等[23]采用有限元法研究了变刚度复合材料的失效性能。

迄今为止，对曲线纤维变刚度复合材料层合板力学性能的研究主要集中在屈曲问题上，而对气动弹性问题的研究还很少。Stodieck等[24-25]研究了矩形机翼的气动弹性性能，对曲线纤维复合材料进行了气动弹性剪裁优化，研究表明，采用曲线纤维复合材料层合板气动弹性性能更好，可以通过改变曲线纤维方向来提高气动弹性稳定性，减缓突风载荷。Stodieck等[26]利用三维有限元模型对直线铺层和曲线铺层蒙皮的性能进行优化，评估了全尺寸气动弹性剪裁机翼的减重能力。优化结果表明，曲线纤维的减重效果比直线纤维更好。Haddadpour和Zamani[27]将曲线纤维复合材料机翼简化为薄壁梁进行了气动弹性设计，对纤维方向沿展向线性变化的变刚度结构进行了最大气动弹性失稳速度的优化。结果表明变刚度机翼的气动弹性稳定性比传统不变刚度的机翼要好。Stanford等[28]对低速流场中曲线纤维悬臂平板进行了气动弹性剪裁设计，采用遗传算法确定静气弹变形和颤振边界，研究了曲线和直线纤维方向和铺层顺序对气动弹性剪裁的影响。

本文以曲线纤维变刚度复合材料层合板为研究对象，建立变刚度复合材料壁板颤振的气动弹性力学模型。研究高速流场中复合材料层合壁板的固有振动特性、颤振稳定性和非线性颤振响应，分析边界条件和铺层方式对变刚度复合材料壁板颤振特性的影响。

1 曲线纤维变刚度复合材料单层板

对图2所示的矩形单层板，其长和宽分别为a和b，纤维方向用T0|T1表示，其中，T0为纤维在板中心处和x方向的夹角，T1为纤维在边界(x=±a/2)处和x方向的夹角。

假设纤维方向从板的中心位置开始呈线性变化，则任意位置处纤维方位角可表示为

(1)

曲线纤维路径为

y(x)=

(2)

2 高速流场中复合材料层合板颤振方程

对于复合材料层合板的颤振问题，考虑von-Karman非线性应变-位移关系，即

(3)

横向剪切应变为

(4)

式中：u0和v0分别为中面上的点沿x和y方向的位移；w为z方向的位移；θx和θy分别为中面绕x轴和y轴的转角；εm为壁板中面面内位移产生的应变；εmb为考虑大变形时，挠度在壁板中引起的面内附加应变；κ为弯曲时壁板的曲率向量；z为壁板厚度方向的坐标。

本构关系可表示为

(5)

对于层数为NL的层合板，令ε0=εm+εmb，内力表达式为

(6)

(7)

式中：A为拉伸刚度矩阵；B为耦合刚度矩阵；D为弯曲刚度矩阵；AS为剪切刚度矩阵；N、M和R分别为面内力、面内力矩和横向剪切力。

对于曲线纤维变刚度复合材料层合板，每一点的纤维方向都是不同的，因此变刚度板的刚度不再是常量，而是随着不同位置处纤维方位角的变化而变化。采用有限元法分析时，需要通过增加网格密度来模拟由于纤维方位角的变化而带来的刚度变化，才能保证分析结果的精度。

对高速流场(Ma>1.6)中的壁板颤振，可由一阶准定常活塞理论计算气动力，壁板表面气流沿x方向时，有

(8)

由虚功原理可得高速流场中壁板的运动方程为

(9)

式中：w为位移向量；M为质量矩阵；C为气动阻尼矩阵；Ka为气动刚度矩阵；KL为线弹性刚度矩阵；N1和N2为大变形产生的非线性刚度矩阵。

高速流场中考虑几何非线性的壁板颤振方程采用Newmark法求解。

为便于后续分析，对壁板颤振动压和频率等参数进行无量纲化，无量纲动压λ和无量纲频率ω*分别为[29]

(10)

式中：D=E2t3，E2为横向弹性模量，t为板的厚度；ρ为板的密度；ω为振动频率。

(11)

式中：W为无量纲振幅；x和y为坐标值。

3 算法验证

3.1 正确性验证

用文献[30]中的四边简支碳/环氧复合材料层合板对本文算法及程序的正确性进行验证。材料属性如表1所示，板的尺寸a=b=0.305 m，板厚为1.27 mm，铺层为[0/45/-45/90]s。采用考虑横向剪切的3节点Mindlin(MIN3)板单元进行有限元分析，整个板用10×10的网格表示，共划分为200个MIN3板单元。分析结果与文献[30]的结果对比如图3所示。可以看出本文结果与文献[30]的结果吻合较好。

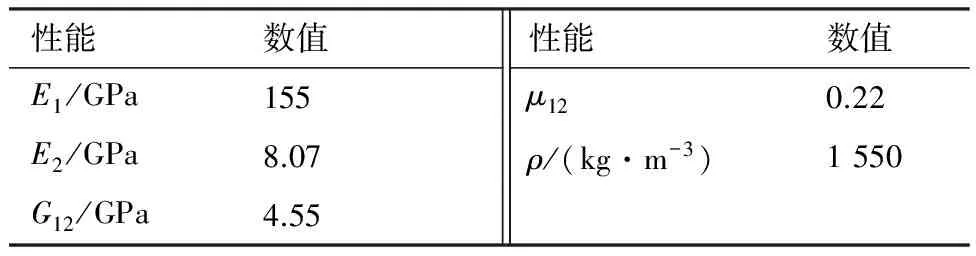
表1 复合材料层合壁板材料性能Table1 Material properties of composite laminates

3.2 网格收敛性研究

考虑四边固支曲线纤维变刚度复合材料层合壁板，其材料属性见表1。几何尺寸为a×b=0.2 m×0.3 m，单层厚度为0.15 mm，铺层为 [0/90/T0|T1/-T0|-T1]s，来流方向平行于x轴。采用有限元法进行分析，单元为考虑横向剪切的3节点Mindlin(MIN3)板单元。

表2 曲线纤维复合材料层合板无量纲颤振动压网格收敛性Table 2 Mesh convergence of non-dimensional flutter dynamic pressure of composite laminates with curvilinear fibers

注：表中的误差以网格100×100为基准进行计算。

综合考虑非线性壁板颤振的计算精度和效率，本文后续计算采用32×15共960个MIN3板单元的网格划分。

4 复合材料层合板颤振稳定性分析

4.1 动力学特性分析

考虑到壁板的动力学特性与颤振特性有密切关系，首先对层合复合材料壁板的固有振动特性进行分析。

计算不同铺层曲线和直线纤维复合材料层合板动力学特性。对[0/90/T0|T1/-T0|-T1]s，考虑T0=0°～45°、T1=45°和T0=45°、T1=45°～90°这2种情况，前6阶固有频率计算结果分别如表3和表4所示。

从表3和表4可以看出，T0和T1对曲线纤维复合材料层合壁板的固有频率均有一定影响。当T1相同而T0不同时，1、4和5阶固有频率随T0增大而减小，而2、3和6阶固有频率随T0的增大而增大。当T0相同而T1不同时，1、2、4和5阶频率随T1增大而减小，而3阶和6阶固有频率随T1增大而增大。这是由于变刚度复合材料层合板内纤维方向的变化而导致刚度不再是常量，而是随着位置的变化而变化引起的。利用这一特点，可以通过调整纤维方向改变复合材料层合壁板的固有振动特性。

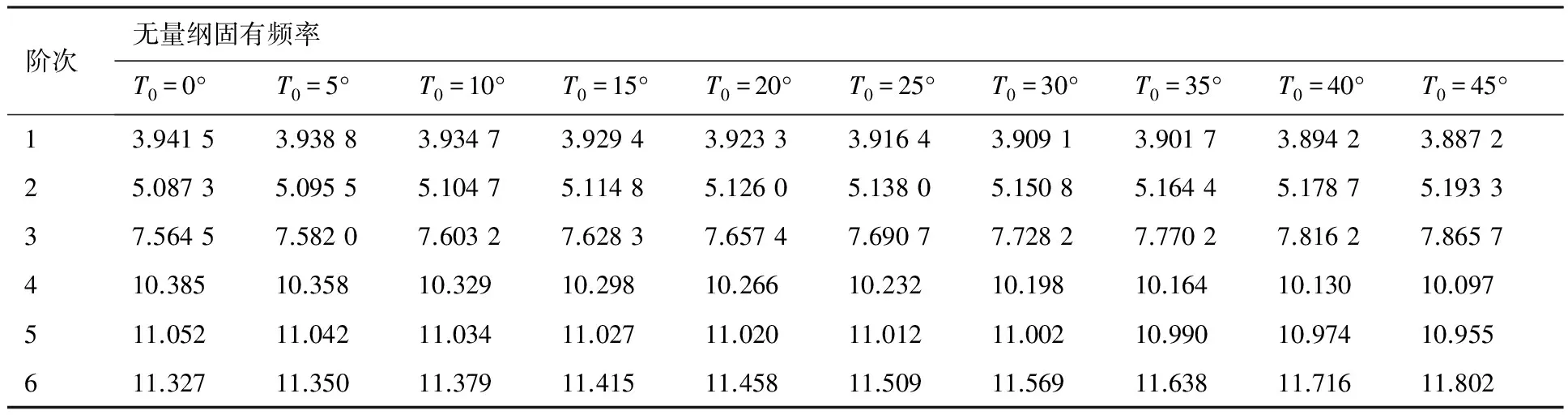
表3 曲线纤维复合材料层合板无量纲固有频率随T0的变化(T1=45°)Table 3 Non-dimensional natural frequency of composite laminates with curvilinear fibers with various T0 (T1=45°)

表4 曲线纤维复合材料层合板无量纲固有频率随T1的变化(T0=45°)Table 4 Non-dimensional natural frequency of composite laminates with curvilinear fibers with various T1 (T0=45°)

4.2 模态耦合分析

对不同铺层曲线和直线纤维复合材料层合板耦合模态进行计算。考虑5种曲线纤维和1种直线纤维层合板，铺层分别取 [0/90/0|15/0|-15]s、[0/90/0|30/0|-30]s、[0/90/0|45/0|-45]s、 [0/90/15|45/-15|-45]s、[0/90/30|45/-30|-45]s和[0/90/±45]s，耦合模态分析结果如图4所示。以[0/90/0|45/0|-45]s和[0/90/±45]s为例进行耦合特性分析，其模态如图5所示。可以看出，当T0相同而T1不同或者当T1相同而T0不同时，颤振均由1阶模态和4阶模态耦合引起。即对上述层合板，耦合模态与T0和T1无关。

4.3 边界条件的影响

对不同边界条件下曲线纤维和直线纤维复合材料层合板颤振特性进行计算。考虑6种不同铺层曲线纤维和1种直线纤维层合板，铺层分别取 [0/90/0|45/0|-45]s、[0/90/15|45/-15|-45]s、[0/90/30|45/-30|-45]s、[0/90/45|60/-45|-60]s、[0/90/45|75/-45|-75]s、[0/90/45|90/-45|-90]s和[0/90/±45]s，马赫数为3，四边简支和四边固支下的计算结果如图6所示。可以看出，边界约束越强，层合板的稳定性越好，颤振临界动压越大。无论是直线纤维还是曲线纤维，四边固支层合板的颤振临界动压均明显高于四边简支层合板。

4.4 曲线纤维方向的影响

计算不同铺层曲线纤维和直线纤维复合材料层合板颤振特性。对[0/90/T0|T1/-T0|-T1]s，考虑T1不变、T0=-90°～90°和T0不变、T1=-90°～90°这2种情况，马赫数取3，计算结果如图7所示。

可以看出，T0和T1对曲线纤维复合材料层合壁板的颤振均有一定影响。T1不变时，颤振临界动压随T0的变化规律一致。当纤维方向逼近x方向时颤振临界动压增加，这是由于层合板x方向的刚度增加。T0不变、T1变化时的变化规律与T1不变、T0变化的情况相同。当T0=T1=0°时，层合板x方向的刚度最大，颤振临界动压达到最大值。可见，通过调整曲线纤维的路径可以改变曲线纤维复合材料层合壁板的颤振临界动压。

5 变刚度复合材料层合板的非线性颤振

5.1 变刚度复合材料层合板的非线性颤振响应

高速流场中曲线纤维变刚度复合材料层合板在给定初始扰动下，若在颤振临界动压以下,层合板的运动随时间减小，则响应是收敛的；当超过临界动压，层合板的振幅随时间增大直到最大振幅，则形成极限环振动。图8和图9分别表示[0/90/±45]s和[0/90/0|45/0|-45]s复合材料层合板的颤振时间历程和相平面图(所取点位于 (0.75a, 0.5b)处)。从图8可以看出，对传统的直线纤维层合板[0/90/±45]s，当λ=510时，壁板受到初始扰动后，振动是收敛的，表明动压未达到颤振临界动压；当λ=520时，壁板受到初始扰动后，处于极限环振动，此时动压超过颤振临界动压，层合板做周期振动，出现颤振。从图9可以看出，对曲线纤维层合板[0/90/0|45/0|-45]s；当λ=550时，壁板受到初始扰动后，随着时间的增加振动是收敛的，表明动压未达到颤振临界动压；当λ=560时，壁板受到初始扰动后，处于极限环振动，此时动压超过颤振临界动压，层合板做周期振动，出现颤振。图10表示t=0.255 s时，[0/90/±45]s和[0/90/0|45/0|-45]s这2种层合板的极限环颤振变形，最大值出现在(0.75a, 0.5b)处。

5.2 曲线纤维方向对非线性颤振响应的影响

对不同铺层的曲线纤维和直线纤维复合材料层合板非线性颤振进行分析。铺层为[0/90/T0|T1/-T0|-T1]s，考虑T0=0°～45°、T1=45°和T0=45°、T1=45°～90°这2种情况，马赫数取3。T0和T1对振幅的影响如图11所示。

可以看出，T0和T1对曲线纤维复合材料层合壁板的颤振均有一定影响。当T1相同而T0不同时，壁板的极限环振幅随T0的增大而增大；当纤维T0相同而T1不同时，壁板的极限环振幅随T1增大而增大。

图12表示不同铺层的变刚度复合材料层合板在不同边界条件时，颤振幅值随动压的变化。可以看出不同铺层和不同边界条件下的颤振幅值随动压的变化趋势基本一致，极限环振幅随动压的增加而增大。不同边界条件下，由于复合材料不同方向的刚度影响，壁板的振幅随T0或T1的增加而增大。固支情况下，T0和T1对振幅的影响更大。

6 结 论

1)T0和T1对曲线纤维复合材料层合壁板的固有振动特性有一定影响，可以通过调整T0和T1改变壁板的固有振动特性。

2)T0或T1对曲线纤维复合材料层合壁板颤振耦合模态的影响不大。

3) 边界条件对复合材料层合壁板的颤振临界动压有较大影响，边界约束越强，壁板的稳定性越好，颤振临界动压越大。

4)T0和T1对壁板的颤振临界动压有较大影响，随着T0或T1的增大，颤振临界动压减小。

5) 直线纤维铺层和曲线纤维铺层的颤振极限环变形最大值都出现在(0.75a, 0.5b)处。

6) 相同的动压下，随着T0或T1的增大，曲线纤维复合材料层合板的极限环振幅增大。

7) 曲线纤维复合材料层合壁板颤振幅值随动压的变化趋势基本一致，极限环振幅随动压的增加而增大，且固支条件下T0和T1对振幅的影响更大。

综上所述，高速流场中，边界条件对曲线纤维复合材料层合壁板的非线性颤振特性有明显影响，采用曲线铺层可根据需要调整壁板的非线性颤振特性，进一步提高复合材料的可设计性。

参 考 文 献

[1] MILES J W. Dynamic chordwise stability at supersonic speeds： Report AL-1140[R]. Dundalk, MD: North American Aviation, Inc., 1950.

[2] JORDAN P F. The physical nature of panel flutter[J]. Aero Digest, 1956, 72(2): 34-38.

[3] OLSON M D. Finite elements applied to panel flutter[J]. AIAA Journal, 1967, 5(12): 2267-2270.

[4] OLSON M D. Some flutter solutions using finite elements[J]. AIAA Journal, 1970, 8(4): 747-752.

[5] KOUCHAKZADEH M A, RASEKH M, HADDADPOUR H. Panel flutter analysis of general laminated composite plates[J]. Composite Structures, 2010, 92(12): 2906-2915.

[6] ABDEL-MOTAGLAY K, CHEN R, MEI C. Nonlinear flutter of composite panels under yawed supersonic flow using finite elements[J]. AIAA Journal, 1999, 37(9): 1025-1032.

[7] SINGHA M K, GANAPATHI M. A parametric study on supersonic flutter behavior of laminated composite skew flat panels[J]. Composite Structures, 2005, 69(1): 55-63.

[8] 王晓庆, 韩景龙, 张军红. 不同气流偏角下的壁板热颤振分析及多目标优化设计[J]. 航空学报, 2010, 31(11): 2195-2201.

WANG X Q, HAN J L, ZHANG J H. Thermal flutter analysis of panel and multi-objective optimization design considering variation of flow yaw angle[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(11): 2195-2201 (in Chinese).

[9] 苑凯华, 邱志平. 含不确定参数的复合材料壁板热颤振分析[J]. 航空学报, 2010, 31(1): 119-124.

YUAN K H, QIU Z P. Thermal flutter analysis of composite panel with uncertain parameters[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(1): 119-124 (in Chinese).

[10] 苑凯华, 邱志平. 高超声速气流中复合材料壁板热颤振分析[J]. 南京航空航天大学学报, 2010, 42(3): 313-317.

YUAN K H, QIU Z P. Flutter analysis of composite panels in hypersonic flow with thermaleffects[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(3): 313-317 (in Chinese).

[11] 杨智春, 谭光辉, 夏巍. 铺层方式对复合材料壁板热颤振特性的影响[J]. 宇航学报, 2008, 29(3): 1047-1052.

YANG Z C, TANG G H, XIA W. Thermal flutter analysis of composite panel with uncertain parameters[J]. Journal of Astronautics, 2008, 29(3): 1047-1052 (in Chinese).

[12] 高扬, 杨智春, 谷迎松. 气流偏角对不同形状复合材料壁板热颤振特性的影响[J]. 振动与冲击, 2014, 33(11): 65-69.

GAO Y, YANG Z C, GU Y S. Effects of flow yaw angle on thermal flutter characteristics of composite panels with differentshapes[J]. Journal of Vibration and Shock, 2014, 33(11): 65-69 (in Chinese).

[13] 吕秀秀, 李凤明, 宋智广. 超声速复合材料层合壁板结构的颤振特性分析[J]. 计算力学学报, 2013, 30(S1): 140-143.

LV X X, LI F M, SONG Z G. Flutter characteristic analysis of supersonic composite laminated panel[J]. Chinese Journal of Computational Mechanics, 2013, 30(S1): 140-143 (in Chinese).

[14] AKHAVAN H, RIBEIRO P. Natural modes of vibration of variable stiffness composite laminates with curvilinear fibers[J]. Composite Structures, 2011, 93(11): 3040-3047.

[15] HYER M W, CHARETTE R F. Use of curvilinear fiber format in composite structure design[J]. AIAA Journal, 1991, 29(6): 1011-1015.

[16] HYER M W， LEE H H. The use of curvilinear fiber format to improve buckling resistance of composite plates with central holes[J]. Composite Structures, 1991, 18(3): 239-261.

[17] GÜRDAL Z, OLMEDO R. In-plane response of laminates with spatially varying fiber orientations: Variable stiffness concept[J]. AIAA Journal, 1993, 31(4): 751-758.

[18] LOPES C S, CAMANHO P P, GÜRDAL Z, et al. Progressive failure analysis of tow-placed, variable-stiffness composite panels[J]. International Journal of Solids and Structures, 2007, 44(25-26): 8493-8516.

[19] GÜRDAL Z, TATTING B F, WU C K. Variable-stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response[J]. Composites: Part A, 2008, 39(5): 911-922.

[20] LOPES C S, GÜRDAL Z, CAMANHO P P. Variable-stiffness composite panels: Buckling and first-ply failure improvements over straight-fiber laminates[J]. Computers and Structures, 2008, 86(9): 897-907.

[21] WU Z, WEAVER P M, RAJU G, et al. Buckling analysis and optimisation of variable angle tow composite plates[J]. Thin-Walled Structures, 2012, 60(10): 63-172.

[22] WU Z, RAJU G, WEAVER P M. Postbuckling analysis of variable angle tow composite plates[J]. International Journal of Solids and Structures, 2013, 50(10): 1770-1780.

[23] 杜宇, 杨涛, 李志猛, 等. 纤维曲线铺放的变刚度复合材料层合板的失效分析[J]. 宇航材料工艺, 2013, 43(5): 22-25.

DU Y, YANG T, LI Z M, et al. Failure analysis of variable-stiffness composite laminates with curvilinear fiber placement[J]. Aerospace Materials & Technology, 2013, 43(5): 22-25 (in Chinese).

[24] STODIECK O, COOPER J E, WEAVER P M, et al. Improved aeroelastic tailoring using tow-steered composites[J]. Composite Structures, 2013, 106: 703-715.

[25] STODIECK O, COOPER J E, WEAVER P M. Optimization of tow-steered composite wing laminates for aeroelastic tailoring[J]. AIAA Journal, 2015, 53(8): 2203-2215.

[26] STODIECK O, COOPER J E, WEAVER P M. Aeroelastic tailoring of a representative wing box using tow-steered composites[J]. AIAA Journal, 2017, 55(4): 1425-1439.

[27] HADDADPOUR H, ZAMANI Z. Curvilinear fiber optimization tools for aeroelastic design of composite wings[J]. Journal of Fluids and Structures, 2012, 33(5): 180-190.

[28] STANFORD B K, JUTTE C V, WU K C. Aeroelastic benefits of tow steering for composite plates[J]. Composite Structures, 2014, 118: 416-422.

[29] PIDAPARTI R M V, YANG H T Y.Supersonic flutter analysis of composite plates and shells[J]. AIAA Journal, 1993, 31(6): 1109-1117.

[30] ZHOU R C, XUE D Y, MEI C. Finite element time domain-modal formulation for nonlinear flutter of composite panels[J]. AIAA Journal, 1994, 32(10): 2044-2052.