基于H∞算法的飞机机翼结冰气动参数辨识

丁娣，车竞，钱炜祺，汪清

1.中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000 2. 中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

飞机飞行过程中的结冰现象是影响飞行安全甚至导致灾难性事故的重要原因之一，国内外发生的多起与结冰相关飞行事故表明开展飞机结冰及其防护相关基础问题研究具有重要而紧迫的意义。飞机结冰探测是结冰防护的前提，从探测方式看主要有直接和间接探测两种，直接探测以各种传感器探测为主[1-2]，间接探测主要有以下3种方式[3]：一是基于状态观测的结冰探测技术，通过探测飞机状态量的异常变化来对结冰进行诊断；二是新息法(Innovation Approach)探测技术，利用统计学工具分析结冰对新息序列(Innovation Sequence)的统计显著性进行结冰诊断；三是基于参数辨识的结冰诊断方法。与直接探测方法相比，间接探测方法一般可以获得更多的结冰相关信息，二者可以互为补充。NASA结冰研究中心就提出了将传感器直接探测与参数辨识技术相结合，建立结冰智能管理系统(Smart Icing System，SIS)[4]的研究思路。

随着飞机结冰智能管理、容错飞行和可重构控制等需求的提出，参数辨识方法在飞机结冰探测领域受到越来越多的关注，通过参数辨识方法不仅能获得飞机结冰累积过程中飞机气动特性参数的变化，而且能够获得参数化的结冰累积模型。在飞机结冰探测中，要求参数辨识算法能够实时快速捕捉由结冰引起的飞机气动特性参数的微小变化，且精度高、响应时间短，并具有一定的鲁棒性，因此滤波算法是一种较好的选择。对于飞机结冰参数辨识问题，需要实时跟踪飞机结冰气动参数，因此属于非线性滤波，目前应用于飞机结冰探测的参数辨识方法主要包括扩展卡尔曼滤波[5-6](Extended Kalman Filter，EKF)、H∞滤波和多模型自适应估计[7](Multiple Model Adaptive Estimator，MMAE)等。扩展卡尔曼滤波作为非线性滤波的经典方法应用非常广泛，但由于EKF自身存在的固有缺陷使得人们不断寻求新的滤波方法[8]，比如专门为鲁棒性设计的H∞滤波，相比EKF，H∞算法能够处理建模误差和噪声不确定性[9]。H∞滤波算法首先由Didinsky等[10]提出并证明其渐进收敛性，由于计算效率高，响应快，且具有一定的鲁棒性，近年来在飞机结冰参数在线辨识中应用较多。Melody等[6]利用NASA双水獭飞机对比了批处理最小二乘算法、扩展卡尔曼滤波和H∞算法在结冰参数辨识中的性能，仿真发现在扰动和测量噪声的影响下，只有H∞算法能够提供实时准确的辨识结果。在此基础上，Melody等[11]进一步探讨了H∞算法在飞机结冰在线识别中的应用，讨论了算法对中度和重度结冰累积过程中飞机气动参数连续变化的跟踪能力。由于H∞算法的鲁棒性较好且在线跟踪能力较强，Melody认为H∞算法适合应用于结冰管理系统(Ice Management System，IMS)[12]。Schuchard等[13]结合Melody的研究内容，在H∞算法参数辨识的基础上结合神经网络方法对飞机结冰位置和严重性进行分类和识别，Dong和Ai[14-15]后续也开展了相似的研究。应思斌等[16]也对H∞算法在飞机结冰参数辨识中的应用进行了探讨，分析了将时变和时不变H∞算法灵活应用于飞机结冰探测的策略[17]，并基于H∞参数辨识和H2控制算法[18]，设计了飞机结冰可重构控制系统。

目前H∞滤波在飞机结冰参数辨识中的研究大部分都是基于NASA的双水獭结冰研究样机，研究中发现当存在测量噪声时算法存在跟踪延时和辨识精度降低的现象，这是由H∞算法本身关于噪声不确定性假设导致的，针对该问题，本文拟通过调节算法中关于噪声不确定性相关参数加以解决。在此基础上，本文针对为满足国内大型飞机结冰防护研究需求而专门设计的大型结冰研究样机，开展基于H∞算法的飞机机翼结冰气动参数辨识方法研究。文中首先介绍了结冰研究样机无冰、中度和重度结冰下的纵向气动导数的CFD拟合结果，建立了考虑结冰累积过程的动力学模型及时变参数H∞辨识算法，利用动力学模型和H∞算法构建能够用于结冰在线探测的仿真框架，通过辨识算例分析了H∞算法参数选择的合理性以及H∞算法用于结冰研究样机气动导数辨识的有效性，最后分析了H∞算法对81种不同结冰累积过程的辨识能力以及不同测量噪声对算法辨识精度的影响。

1 结冰研究样机

为了满足大型飞机的研制需求，分析结冰对大型飞机气动特性的影响，课题组专门构建了与C919、Boeing737和空客A320外形相近的大型飞机作为该结冰项目的研究样机，该样机同时具备大型飞机的基本空气动力学和飞行力学特征，其外形结构如图1所示，几何物理参数如表1所示。

结冰研究样机的气动特性数据由CFD手段得到，基于雷诺平均Navier-Stokes(RANS)方法和多块结构化网格技术对结冰研究样机进行基本气动力计算，得到了干净外形及机翼中度和重度结冰下的纵向气动特性，机翼中度和重度结冰对应的冰型如图2所示。

表1 结冰研究样机几何参数Table 1 Geometric parameters of icing research prototype

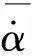
表2 结冰研究样机无冰及结冰情况下的气动导数

2 飞机结冰气动参数辨识方法及算例

首先推导了考虑结冰累积过程的飞行动力学模型以及能够用于时变参数辨识的H∞滤波算法，利用动力学模型和参数辨识算法构建可用于飞机结冰在线探测的仿真框架，在此基础上讨论了辨识算法参数对辨识精度的影响，并由仿真算例分析了气动导数的辨识误差及结冰预报延时。

2.1 飞机结冰飞行动力学模型

建立考虑结冰累积过程的飞机纵向运动方程，在速度坐标系下建立质心运动方程，在体坐标系下建立转动方程，则飞机的纵向动力学方程可表示为

Vsinαcosβcosθcosφ

(1)

式中:V为飞机合速度；α为迎角；β为侧滑角；p为滚转角速率；q为俯仰角速率；r为偏航角速率；θ为俯仰角；φ为滚转角；h为离地高度；q∞为动压；P=[PxPyPz]为发动机推力；M=[MxMyMz]为发动机推力力矩；g=[gxgygz]为重力加速度矢量，下标x、y和z表示相应坐标系下的坐标；CD、CL和Cm分别为阻力、升力和俯仰力矩系数，其中阻力、升力和俯仰力矩系数相关气动导数取值见表2,表达式为

(2)

飞机结冰会引起阻力、升力和俯仰力矩系数的变化，描述结冰对飞机气动特性的影响需要建立气动导数在结冰累积过程中的变化模型。伊利诺斯大学的Bragg等[4]提出了一种描述结冰对气动导数影响的数学模型，该模型虽然不能完全精确反应结冰对气动导数的影响，但是通过该模型能够获得结冰前后气动导数的一般变化趋势，且能够用于智能结冰系统的开发，目前已被应用于飞机结冰在线识别技术的讨论[7,11,15]。结冰对飞机气动导数的影响可表示为

(3)

式中：C*表示飞机的任意气动导数，上标“iced”表示结冰后的气动导数，“clean”表示干净外形的气动导数；ηice为结冰严重性参数；KC*为气动导数变化斜率，由结冰前后气动导数大小决定。ηice=0表示干净外形的气动特征，ηice=1表示机翼结冰后飞机的气动特征，通过构造ηice的变化曲线来近似飞机气动导数受结冰影响后的变化过程。Melody等[11]给出了一种反应结冰连续增长的结冰模型，考虑了结冰过程同时受大气环境因素和冰累计量的影响，将ηice的变化记为

(4)

式中:N1和N2为常数，与不同时刻的结冰严重性参数大小相关，N2代表式(4)的非线性程度，N2>0为冰增长过程，N2<0为冰退化过程，二者可表示为

(5)

式中:Tcld为结冰累积时间。

式(4)为结冰增长模型，dη表征大气环境对结冰的影响，这里将其表示为上升余弦函数，即

(6)

当Tcld、ηice(Tcld/2)和ηice(Tcld)已知时，由式(3)～式(6)能够给出飞机任意气动导数受结冰影响随时间的变化曲线，其中ηice(Tcld/2)和ηice(Tcld)的取值表征不同结冰累积时间对应的结冰严重性系数，可以反应结冰累积速度。

2.2 H∞时变参数辨识方法

将式(1)对应的飞行动力学系统写成参数化形式[10]，即

(7)

(8)

(9)

将式(4)代入式(9)，得

(10)

在初始时刻ηice=0，那么联立式(6)、式(8)、式(10)，得

(11)

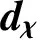
(12)

(13)

根据二次型变换，由式(13)可推导出H∞滤波算法，即

(14)

式中：Σ∈R(n1+n2)×(n1+n2)，n1为系统状态量维度，n2为系统未知参数维度，则Σ1∈n1×n1，当选取P0=I，以及时，对所有Q0>0都有γ*≡1成立。

2.3 算法参数调节及辨识结果分析

利用辨识算例来说明H∞算法在飞机结冰参数辨识中的有效性，由于目前缺乏飞行试验数据，只能采用仿真数据作为系统辨识依据。

假定飞机在定直平飞情况下机翼出现结冰，结冰累积过程由式(3)描述，其中Tcld=200 s，ηice(Tcld)=1.0，ηice(Tcld/2)=0.7，飞机巡航高度为5 000 m，飞行速度为马赫数0.3，升降舵偏输入信号幅值为3°、周期为40 s的正弦信号。考虑测量噪声的影响，假设噪声为高斯白噪声，其标准差取值参照A340的传感器测量精度，如表3[21]所示。在该初始条件下生成考虑测量噪声的动力学仿真数据，利用H∞算法辨识受机翼结冰影响较大的3个与迎角相关的气动导数，即CDα、CLα和Cm α，对辨识结果进行分析以评估H∞算法的辨识精度。

表3 测量噪声标准差[21]Table 3 Standard deviations of measurement noises[21]

由H∞算法推导，算法初始需要确定的参数包括Q0和γ，且参数的取值会对辨识结果产生影响。对于扰动衰减水平γ，根据Didinsky的研究结果，当γ的取值接近且不等于γ*时，算法收敛效果最好[10]；Q0为系统未知参数初始偏差的权值矩阵，由于这一偏差的存在使得Q0的取值会对辨识结果产生影响。Melody等在对NASA的双水獭结冰研究样机进行结冰气动参数辨识研究时，将这两个参数分别取为γ=1.01，Q0=(1×10-5)I，针对两种不同结冰累积情况对Cm α变化情况进行跟踪，发现辨识结果相对真值存在较大的跟踪延时，见表4[11]。

表4 双水獭飞机结冰预报延时[11]Table 4 Delays in ice detection of Twin Otter Airplane[11]

根据以上分析，对于本文的问题，可将γ的取值设为与双水獭飞机算例一致，通过调节矩阵Q0对角线上的元素取值来达到提高参数辨识精度以及减小预报延时的目的。

利用前面推导的飞机动力学模型和参数辨识算法，构建含动力学仿真和H∞参数辨识为一体的结冰在线探测框架，将前面所给仿真初始条件和算法参数代入仿真框架，得到3个受结冰影响较为严重的气动导数辨识结果，根据辨识结果与真值之间的平方根误差(Root Mean Square，RMS)分析矩阵Q0的3个对角线元素{q11,q22,q33}对3个气动导数辨识精度的影响，如表5所示。表中对每个矩阵对角线元素选取3个不同点，通过H∞算法对参数的27种组合分别进行辨识，得到3个气动导数相对真值归一化后的平方根误差，对每个矩阵元素相同的结果取平均，得到每一矩阵元素取值对应的气动导数辨识精度。由表中数据可知，q11主要对CDα的辨识精度产生影响，对CL α和Cm α的影响几乎可以忽略，且q11越小辨识误差越大；q22主要对CL α和Cm α的辨识精度产生影响，对CD α影响相对较小，q22越小CL α和Cm α的辨识精度越高；q33对Cm α影响相对较大，对CD α影响相对较小，对CL α影响几乎可以忽略，q33越小Cm α的辨识精度越高。根据以上分析，这里将矩阵Q0设为Q0=diag(1,10-5,10-5)。

表5 矩阵Q0对气动导数辨识精度的影响

将前面确定的H∞算法参数代入结冰在线探测框架，得到气动导数辨识结果，如图3和图4所示。图3中给出了CD α、CL α和Cm α3个气动导数在结冰累积影响下的辨识结果与真值之间的对比，图4中给出了由式(3)将辨识结果表示为结冰严重性参数后与真值的对比，图中黑色虚线为移动平均滤波器(Moving Average Filter)平滑后的辨识结果。由图中结果可知，CL α和Cm α的辨识结果较为平滑，CD α在气动导数变化阶段振荡相对比较明显，这说明通过前面调节加权矩阵Q0能够有效减小CL α和Cm α的振荡，但CD α的振荡现象难以消除；当结冰累积过程结束后，辨识结果能够收敛到真值附近，即趋近于重度结冰后的气动导数取值；在结冰累积阶段，辨识结果存在一定程度上的时间延迟，其中CD α的延迟较为严重，Cm α次之，CL α最好。

为了对辨识结果进行评估，定义了平方根误差、最大绝对误差和结冰严重性参数分别为0.25、0.50、0.75和0.95对应的时间延迟作为评估的指标，为了保证数据的可比性，这里针对归一化后的结冰严重参数来评估，其中误差和时间延迟的定义均相对气动导数真值给出，时间延迟的计算采用了数据平滑后的结果。表6中给出了辨识结果的误差及结冰严重性参数预报延迟，由表中数据可知，无论是辨识误差还是时间延迟，都是CL α辨识结果最好，Cm α次之，CD α最差。由该算例的辨识结果分析，发现3个气动导数的辨识结果平方根误差较小，其中辨识效果最差的CD α的平方根误差也在真值的11%左右，辨识效果最好的CLα仅为真值的1.4%；最大绝对误差CL α仅为真值的7.8%，Cm α为16.4%，而效果最差的CD α为41%左右，这可能是由辨识结果出现振荡导致的；如果分别以3个气动导数的辨识结果作为结冰探测的依据，那么CD α最大会有20 s左右的预报延迟，Cm α的预报延迟在10 s以内，CL α的预报延迟在3 s以内。同时，表6中Cm α的预报延时明显小于表4中的双水獭飞机算例，说明通过调节算法加权矩阵参数能够提高算法对飞机结冰的在线探测能力。

表6 辨识结果误差及结冰预报延时Table 6 Identification results errors and ice detection delays

因此，对于结冰研究样机机翼结冰情况，通过3个气动导数的辨识结果均可对结冰严重性程度进行预报，但三者的辨识精度和预报延迟差别较大，可以从中选择预报效果最好的参数辨识结果作为结冰在线探测的依据。

3 飞机机翼结冰探测精度

为了评估H∞算法在不同工况下的结冰探测能力，下面通过仿真分析不同结冰累积过程以及测量噪声大小对辨识结果的影响。

3.1 结冰累积过程影响分析

考虑结冰累积时间Tcld和ηice(Tcld/2)取值的变化，可以得到不同的结冰累积过程，利用H∞算法对不同结冰累积过程进行辨识，通过辨识结果误差可评估算法对结冰累积过程的辨识能力。这里将结冰累积时间Tcld的取值区间定为[50,450]s，ηice(Tcld/2)的取值区间定为[0.1,0.9]，不考虑测量噪声的影响，分析辨识结果与真值之间的误差以及不同结冰水平对应的时间延迟，如图5～图7和表7所示。

图5和图6给出了不同结冰累积过程下的平方根误差和最大绝对误差结果，由于平方根误差在结冰累积时间较长时会显著增大，为了便于分析，因此将结果分成了两部分，见图5(a)和图5(b)。图5和图6中分别给出了81种不同结冰累积过程对应的CD α、CL α和Cm α辨识结果与真值之间的误差，为了便于对比3个气动导数辨识误差,分别用不同颜色的标记区分。对于平方根误差，当Tcld≥350 s且ηice(Tcld/2)≤0.7时，3个气动导数均显著增大，最大可达真值的50%左右，其余结冰累积情况下平方根误差均较小，最大约为真值的10%左右，这说明当结冰时间过长且累积速度缓慢时，比较不容易得到准确的辨识结果；对于这81种不同的结冰情况，其中CL α的平方根误差最小的情况占95%，CD α最小的情况占5%，而CD α在60%的情况下误差最大，Cm α在40%的情况下误差最大；且当ηice(Tcld/2)取值在0.4～0.7之间时，CD α辨识误差相对较大，其余取值情况Cm α辨识误差相对较大，说明当结冰累积速度较慢或较快时Cm α辨识结果更不准确。对于最大绝对误差，其结果与平方根误差的分析结果近似，同样对于结冰时间较长且结冰速度较慢的情况,辨识最大误差绝对值会较大；而约有89%的情况下CL α的辨识最大绝对误差最小，6%的情况下CDα最小，5%的情况下Cm α最小；相应的CD α有62%的情况辨识最大绝对误差最大，Cm α有38%的情况辨识最大绝对误差最大。

对辨识结果关于不同结冰水平的时间延迟进行分析，发现当结冰累积时间较长时存在算法无法跟踪得到相应结冰水平的情况。图7中给出了不同结冰累积情况下的3个气动导数辨识结果分别在0.25、0.50、0.75和0.95这4个结冰水平上的跟踪失败情况，由图可知跟踪失败的情况主要集中在结冰累积时间300～450 s之间。若算法无法跟踪结冰水平为0.25的情况，那么意味着大于0.25的情况也无法跟踪，因此图中4个不同结冰水平的跟踪失败标记呈从高水平向低水平覆盖的状态，且逐渐向(450, 0.1)边界点收缩，其中CDα、CLα和Cmα在不同结冰水平下的预报延时和跟踪失败次数统计见表7，由表中数据可知CLα的跟踪失败次数最少，延时均值最小，说明CLα跟踪更为准确，表中延时标准差在结冰水平为0.25和0.95时较大，这可能是由于辨识结果振荡造成延时散布较大。

根据以上分析，CL α的辨识精度相对其余两个气动导数较高，下面根据CL α的平方根误差和最大绝对误差大小，分析81种结冰累积过程的相对辨识精度，如图8所示。图中以不同颜色对81种结冰累积过程的辨识精度进行区分，偏蓝为辨识精度较高，偏红为辨识精度较差。由图可知，结冰累积时间对辨识精度影响较明显，累积时间较长(>300 s)和较短(50 s)辨识精度稍差，累积时间适中(100～300 s)辨识精度较高，对于ηice(Tcld/2)，累积时间较短和较长对辨识精度有一定影响，当累积时间较长时(>300 s)，结冰累积速度越快辨识精度越高，当累积时间较短时(50 s)，ηice(Tcld/2)取值适中(约为0.3),辨识精度较高。这一结果与H∞算法对飞机结冰气动参数变化的捕捉能力相关，参数变化率太大或太小均会影响算法辨识精度，只有参数变化率适中才能得到精度较高的辨识结果。

表7 不同结冰水平下预报延时及失败次数统计Table 7 Delay and failure statistics in different icing levels

3.2 随机噪声影响下的气动导数辨识精度

由于实际飞行过程中测量噪声的存在，必然会影响结冰气动导数辨识精度，为了对实际飞行过程中基于H∞的结冰气动导数辨识精度进行定量评估，下面在给定测量噪声标准差大小范围下进行多次蒙特卡罗仿真，分析结冰气动导数的辨识精度。

为了尽量覆盖实际可能出现的噪声情况，以表3中A340的传感器精度为基础，将测量噪声标准差变化范围取为从0到表中对应的10倍大小，在该范围内随机均匀生成大量测量噪声标准差作为辨识精度分析的输入条件，根据每一标准差生成高斯随机噪声代入仿真辨识框架，对每一飞机结冰气动导数辨识结果精度进行统计，得到给定噪声标准差变化范围下气动导数辨识精度。蒙特卡罗仿真次数的选择需要分析气动导数辨识结果误差的收敛性，表8中给出了CDα、CLα和Cmα不同蒙特卡罗仿真次数对应平方根误差的统计均值，由表中数据可知对于4 000、5 000和6 000次仿真，3个气动导数的平方根误差的统计均值几乎没有变化，已接近于收敛，因此根据 6 000次蒙特卡罗仿真结果分析3个气动导数的H∞算法辨识精度具有一定的意义。

表8 不同蒙特卡罗仿真次数下的气动导数平方根误差统计均值

表9和表10中给出了CDα、CLα和Cmα3个气动导数辨识结果的平方根误差、最大绝对误差和4种不同结冰水平预报延时按正态分布拟合得到的统计均值μ、标准差σ以及二者的95%置信区间范围μci和σci。由表中数据可知，对于平方根误差和最大绝对误差，从统计均值和标准差可知，都有CDα误差最大，Cmα次之，CLα误差最小，其中辨识效果最好的CLα平方根误差均值为1.8%左右，最大绝对误差均值为8%左右，Cmα的平方根误差均值为4%左右，最大绝对误差均值为19%，而CDα的平方根误差均值为52%，最大绝对误差均值高达250%，这说明在测量噪声影响下，CDα的辨识结果可信性较低，而CLα和Cmα能够得到较为准确的辨识结果。由表10中数据可知，对于不同结冰水平下的预报延时统计结果，由于CDα辨识精度较差，6 000次仿真中出现了6次利用CDα辨识结果无法跟踪结冰系数为0.95的情况，且统计均值出现了负值，说明CDα跟踪结果在结冰累积后期出现了较大的振荡，根据辨识结果跟踪该结冰系数出现了早于真值的情况；对4种不同结冰水平，3个气动导数的预报延时统计均值除CLα明显较小之外，CDα和Cmα相当，但统计标准差CDα明显大于其余二者，说明由于CDα的辨识精度较低导致结冰预报时间延时散布较大；根据统计结果，4种不同结冰水平下CLα的预报延时均值最大为3 s左右，

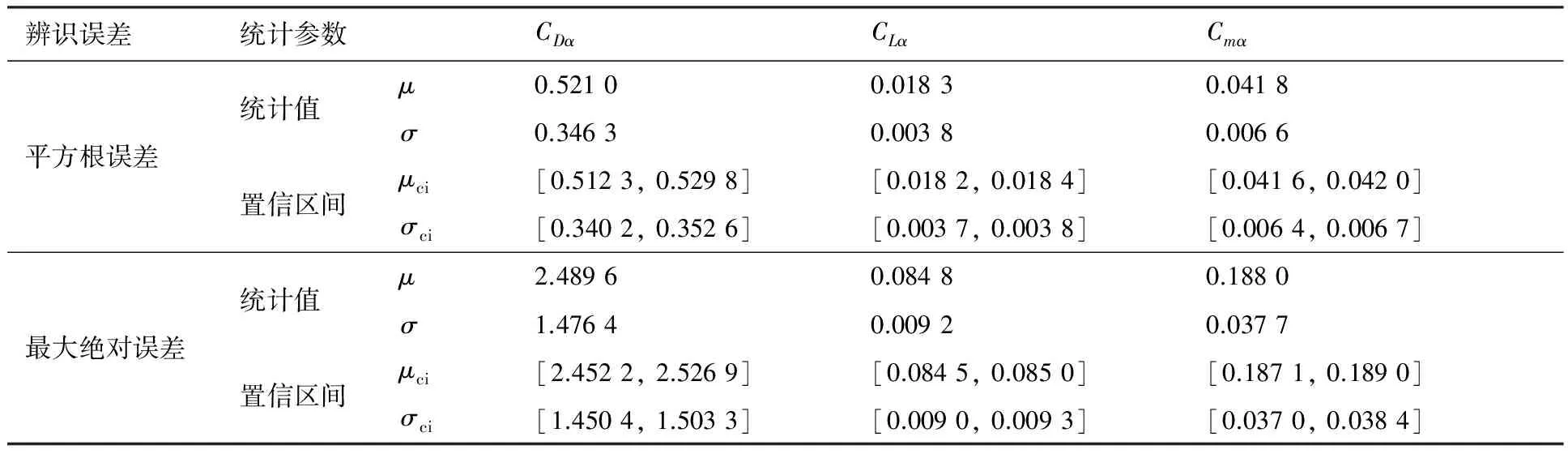
表9 气动导数辨识结果平方根误差和最大绝对误差统计Table 9 Statistics of RMS and maximum absolute errors of identification results of aerodynamic derivatives

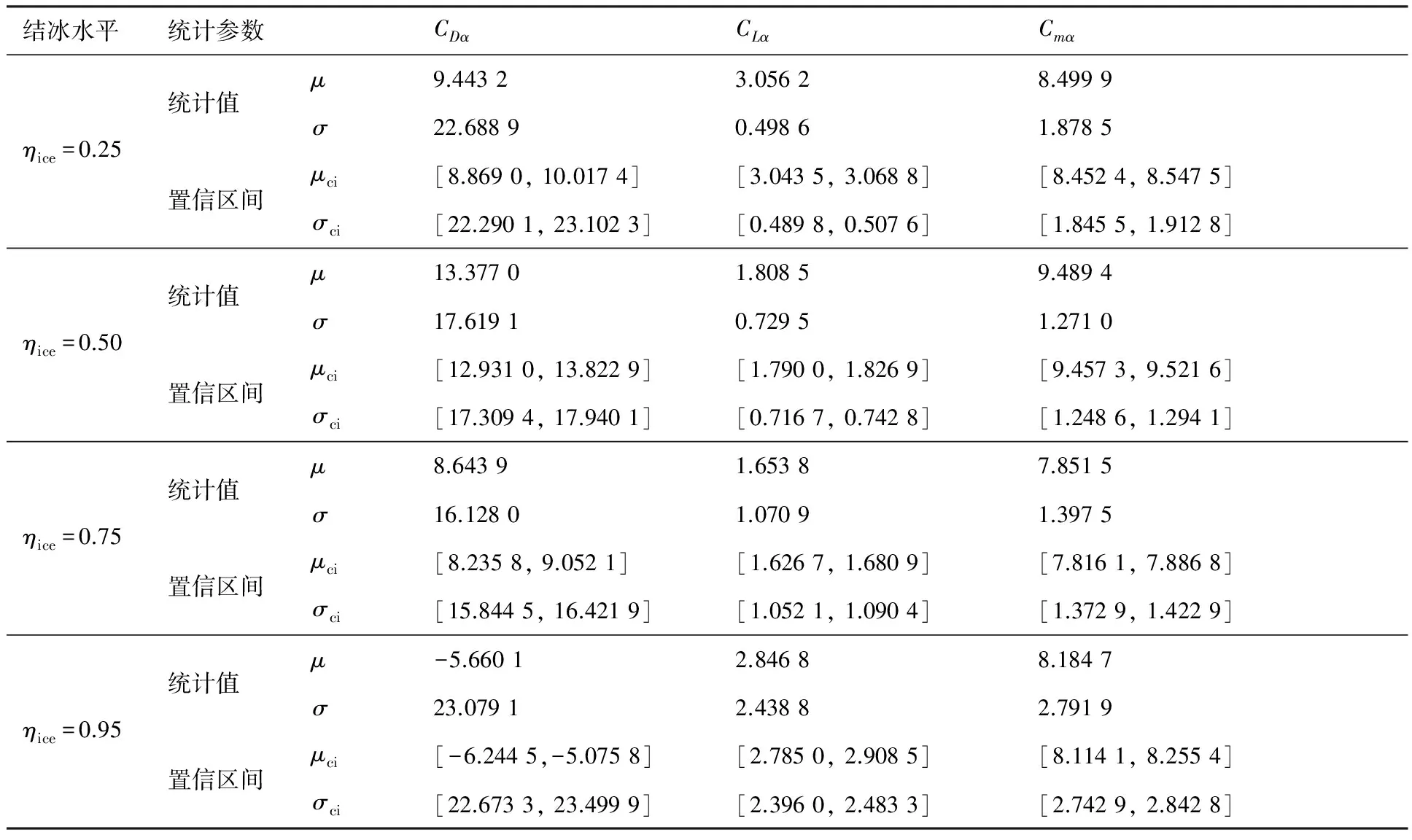
表10 不同结冰水平下气动导数辨识延时统计Table 10 Delays in aerodynamic derivatives identification in different icing levels

统计标准差随结冰水平增大而增加，最大不超过2.5 s，Cmα的跟踪延时均值最大不超过9.5 s，统计标准差最大为2.8 s左右。

4 结 论

1) 调节H∞算法中的加权矩阵会对辨识精度产生影响，通过选择合适的算法参数使得H∞算法能够对结冰研究样机气动导数结冰累积过程进行有效辨识，其中辨识效果最差的CDα的归一化平方根误差为真值的11%左右，辨识效果最好的CLα仅为真值的1.4%。

2) 当参数变化率太快或太慢时H∞算法辨识精度会降低，当参数变化率适中，即结冰累积时间适中(100～300 s)时，算法辨识精度较高，这与H∞算法对时变参数变化的捕捉能力相关。

3) 在测量噪声影响下，CDα的辨识结果可信度较低，而CLα和Cmα能够得到较为准确的辨识结果，在文中给定的测量噪声标准差变化范围内，CLα归一化后的平方根误差均值为1.8%左右，Cmα的平方根误差均值为4%左右，4种不同结冰水平下CLα的预报延时均值最大为3 s左右，Cmα的预报延时均值最大不超过9.5 s。

4) 由大量辨识结果分析可知，对于受机翼结冰影响较为严重的3个气动导数，在结冰累积时间适中的情况下，都有CLα和Cmα辨识结果较好，CDα较差，这与飞机本身的气动特性相关，由于CDα相对CLα和Cmα为小量，因此H∞时变参数模型建模偏差和测量噪声等扰动导致CDα辨识结果容易出现振荡，辨识精度降低，在实际结冰探测中，可以选择法向气动导数和俯仰力矩导数作为辨识对象。

本文的研究工作可以作为大型飞机结冰防护系统研究的基础，为开展虚拟飞行结冰探测提供算法支持，得到的算法辨识精度定量分析结论可为后续工作的开展提供重要的评估依据。下一步还可以结合可重构控制开展基于结冰研究样机的结冰防护相关研究。

参 考 文 献

[1] GORAJ Z.An overview of the deicing and anti-icing technologies with prospects for the future[C]∥24th International Congress of Aeronautical Sciences, 2004.

[2] JARVINEN P. Aircraft ice detection method: AIAA-2007-696[R].Reston, VA: AIAA, 2007.

[3] CALISKAN F, HAJIYEV C. A review of inflight detection and identification of aircraft icing and reconfigurable control[J]. Progress in Aerospace Sciences, 2013, 60: 12-34.

[4] BRAGG M B, BASAR T, PERKINS W R, et al. Smart icing systems for aircraft icing safety: AIAA-2002-0813[R]. Reston, VA: AIAA, 2002.

[5] WENZ A, JOHANSEN T A. Icing detection for small fixed wing UAVs using inflight aerodynamic coefficient estimation[C]∥IEEE Conference on Control Applications. Piscataway, NJ: IEEE Press, 2016.

[6] MELODY J W, BASAR T, PERKINS W R, et al. Parameter identification for inflight detection and characterization of aircraft icing[J]. Control Engineering Practice, 2000, 8(9): 985-1001.

[7] CRISTOFARO A, JOHANSEN T A, AGUIAR A P. Icing detection and identification for unmanned aerial vehicles: Multiple model adaptive estimation[C]∥European Control Conference, 2015.

[8] 占荣辉，张军. 非线性滤波理论与目标跟踪应用[M]. 北京：国防工业出版社，2013: 8-11.

ZHAN R H, ZHANG J. Nonlinear filtering theory with target tracking application[M]. Beijing: National Defense Industry Press, 2013: 8-11(in Chinese).

[9] SIMON D. 最优状态估计:卡尔曼,H∞及非线性滤波[M].张勇刚, 李宁, 奔粤阳, 译. 北京：国防工业出版社，2015: 255-269.

SIMON D. Optimal state estimation: Kalman,H∞and nonlinear approaches[M]. ZHANG Y G, LI N, BEN Y Y, translated. Beijing: National Defense Industry Press, 2015: 255-269(in Chinese).

[10] DIDINSKY G, PAN Z, BASAR T. Parameter identification for uncertain plants usingH∞methods[J]. Automatica, 1995, 31(9): 1227-1250.

[11] MELODY J W, HILLBRAND T, BASAR T, et al.H∞parameter identification for inflight detection of aircraft icing: The time-varying case[J]. Control Engineering Practice, 2001, 9(12): 1327-1335.

[12] MELODY J W. Inflight characterization of aircraft icing[D]. Illinois Urbana: University of Illinois at Urbana-Champaign Graduate College, 2004: 1-6.

[13] SCHUCHARD E A, MELODY J W, BASAR T, et al. Detection and classification of aircraft icing using Neural Networks: AIAA-2000-0361[R]. Reston, VA: AIAA, 2000.

[14] DONG Y Q, AI J L. Research on inflight parameter identification and icing location detection of the aircraft[J]. Aerospace Science and Technology, 2013, 29(1): 305-312.

[15] DONG Y Q, AI J L. Inflight parameter identification and icing location detection of the aircraft: The time-varying case[J/OL]. Journal of Control Science and Engineering, 2014: 1-11. [2014-07-10].http://dx.doi.org/10.1155/2014/396532.

[16] 应思斌, 葛彤, 艾剑良. 飞机结冰时不变参数辨识技术[J]. 指挥控制与仿真, 2012, 34(4): 55-60.

YING S B, GE T, AI J L. Time invariant parameter identification of inflight aircraft icing[J]. Command Control & Simulation, 2012, 34(4): 55-60(in Chinese).

[17] 应思斌, 葛彤, 艾剑良. 飞机结冰气动参数综合检测方法研究[J]. 指挥控制与仿真, 2012, 34(5): 128-133.

YING S B, GE T, AI J L. Research on comprehensive parameter identification of inflight aircraft icing[J]. Command Control & Simulation, 2012, 34(5): 128-133(in Chinese).

[18] YING S B, GE T, AI J L.H∞parameter identification and H2feedback control synthesizing for inflight aircraft icing[J]. Journal of Shanghai Jiaotong University, 2013, 18(3): 317-325.

[19] RATVASKY T P, RANAUDO R J. Icing effects on aircraft stability and control determined from flight data: AIAA-1993-0398[R]. Reston, VA: AIAA, 1993.

[20] BRAGGM B, HUTCHISON T, MERRET J, et al. Effect of ice accretion on aircraft flight dynamics: AIAA-2000-0360[R]. Reston, VA: AIAA, 2000.

[21] AYKAN R, HAJIYEV C, CALISKAN F. Aircraft icing detection, identification and reconfigurable control based on Kalman filtering and neural networks: AIAA-2005-6220[R]. Reston, VA: AIAA, 2005.