大型柔性起重臂系统回转吊装刚柔耦合动力学模型
2018-03-28颜世军刘运思湖南科技大学土木工程学院湖南湘潭411201
颜世军, 彭 剑, 刘 泽, 刘运思(湖南科技大学 土木工程学院, 湖南 湘潭 411201)
超大吨位轮式起重机臂架结构形式复杂,在回转吊载时承受较大的惯性力和吊重偏摆力,对其动态载荷预估不足易导致折臂与倾翻等问题。传统的动载系数折算法与运动弹性动力学分析方法由于对臂架的刚柔耦合特性预估不足[1],在对柔性臂架系统进行动力学性能评估时具有明显的局限性。
起重机臂架系统是由吊臂与吊物等组成的多柔体系统,其动力学特性具有明显的刚柔耦合性质。多柔体动力学近年已成功现代工程领域,并得到了长足的发展[2-3],然在起重机动态吊装领域的应用起步较晚,诸多问题尚需解决。Sato等[4]建立了关于汽车起重机的多柔体动力学模型,仅能对中小型起重臂在起升冲击下进行动力学分析。兰朋等[5]使用梁单元建立臂架和塔身的二维柔体动力学模型,成功分析了塔式起重机在回转过程中的动特性并得到实验的验证,该模型不能预测吊重的偏摆效应。嘉红霞等[6]建立了考虑臂架弹性的动臂起重机的一个简单模型及完全多体动力学模型,该模型能预测动臂起重机变幅吊装下的动态性能。Ku等[7]针对双吊臂船用起重机,考虑水的随机激励因素,建立了递推格式的正向和逆向起重机起升和变幅动力学模型,模型忽略了吊臂的弹性振动。 Sochacki[8]采用多刚体模型描述起重臂,分析了地基弹性对起重机回转作业动态性能的影响。黄毅等[9]基于模态综合法,建立了针对超长柔长臂泵车臂架的简易动力学模型,并采用模态滤波技术及最优极点配置算法进行振动主动控制策略设计,得到了较满意的减振效果。
臂架系统在回转作业时同时含有大范围的刚体转动、吊臂与钢丝绳弹性振动以及吊重的空间摆动,对于大型起重臂,其刚柔耦合效应尤为明显。本文采用混合坐标系[10]进行臂架运动学描述,利用固结于回转中心的惯性系描述臂架与吊重的刚体运动,采用固结于各臂段及钢丝绳的动参考系描述各弹性构件的弹性振动,从拉格朗日分析力学出发,建立了针对大型臂架系统的多柔体动力学模型,对某超大吨位轮式起重机臂架回转吊载工况进行了动力学仿真计算,并与试验对比分析表明了模型的准确性。
1 臂架系统动力学模型
超大型臂架系统结构形式复杂,由弹性吊臂系统(图1)和吊物系统(图3)两部分构成,忽略下车支撑的弹性变形影响,分别对回转作业下的复杂弹性吊臂及钢丝绳吊物系统进行建模,考虑二者之间的约束关系,建立臂架系统的动力学分析模型。
1.1 吊臂回转刚柔耦合动力学模型
图1所示的大型吊臂由箱型主臂,桁架副臂,塔臂撑杆及拉板,超起桅杆及钢丝绳组成,主臂、副臂、撑杆及桅杆在变幅平面内相互铰接,在回转平面内相互固接,主臂各级伸缩臂臂头搭接处约束径向平移,臂尾处约束径向平移及轴向运动。考虑箱型主臂、桁架副臂以及桅杆各部件为细长结构,利用梁单元或等效梁单元离散,拉板和钢丝绳只承受轴向拉力,采用杆单元模拟。

图1 起重机臂架结构
对任意部件i如图2,以固结于回转中心的惯性坐标系xyz描述刚体转动,利用固结于其根部的浮动坐标系xiyizi来描述弹性变形。部件i上任意一点在惯性坐标系下的矢径为
ri=Ri(ri0+xi0+Nqf)
(1)
式中:ri0为惯性坐标系原点在部件i浮动坐标系下的矢径;xi0为部件中任意一点在浮动坐标系下的初始位置;Nqif为部件上任意一点的变形;qif为单元节点位移;N为单元形函数;Ri为任意时刻该浮动坐标系与惯性坐标系的坐标变换矩阵
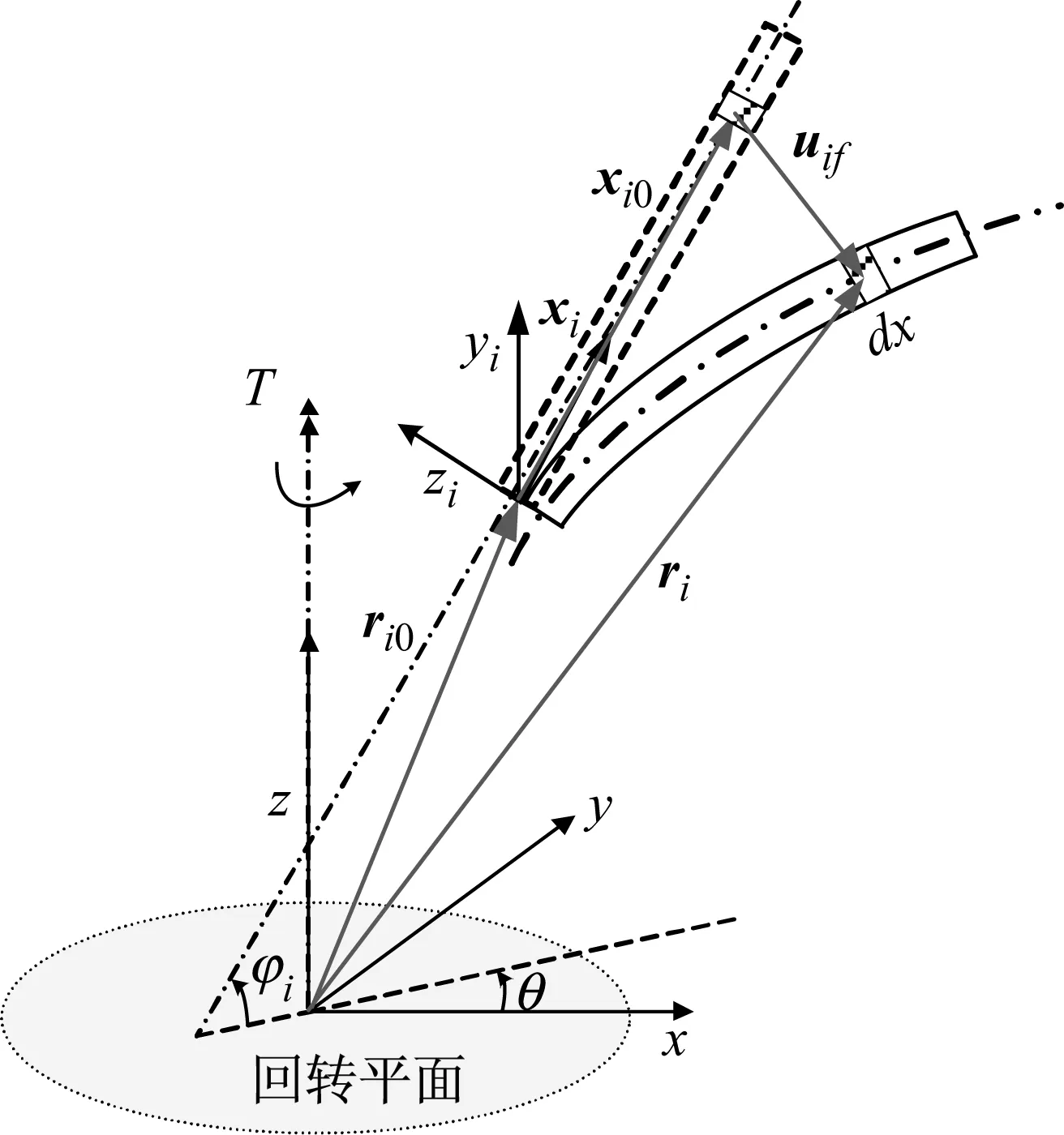
图2 部件回转动力学示意图
式中:θ为任意时刻的回转角度;φi为部件i仰角,进一步,该点的速度为
(2)

(3)

超长柔性吊臂在吊载时呈现明显的大挠度状态,为此考虑几何非线性下弹性吊臂的弹性势能写为
(4)

由拉格朗日动力学方程
(5)
考虑式(3)和(4),可得无阻尼作用下吊臂的刚柔耦合动力学模型为
(6)
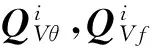
1.2 吊物系统动力学模型
吊物系统由吊重钢丝绳和吊重组成,由于离心惯性力和科式惯性力的影响,吊重在臂架回转时具有球摆特性,其回转摆动描述如图3,以惯性系x′y′z′描述臂头拉点与吊重的刚体运动,固结在钢丝绳臂头处的动参考系xyz钢丝绳的弹性振动,钢丝绳可看作为一单向拉升不考虑质量的弹性连杆,则吊重任意时刻的矢径为

图3 吊物系统回转摆动示意图
(7)

式中:α和β分别为绕当前x轴和y轴转动的欧拉角。由矢径对时间的导数,可得速度为
(8)

进一步,吊重动能为
(9)
式中:mq为吊重质量;Mrr,Mϑϑ分别对应于吊重刚体平动与摆动的质量项;Mrϑ为平动与摆动的耦合质量项;Mll为钢丝绳弹性变形质量项;Mrl,Mϑl分别为平动、摆动与钢丝绳弹性伸长耦合质量项。
吊物系统的势能包含了吊重的势能与钢丝绳的弹性势能
U=mqg[z-(l0+Δl)cosβcosα]+
(10)
式中:Kg为钢丝绳刚度Kg=EgAg/l0;Eg为钢丝绳弹性模量;Ag为钢丝绳截面积;z为臂头处在惯性坐标系下的铅锤位置。
由拉格朗日方程可得无阻尼作用下吊物系统的动力学方程有限元列式为
(11)
式中:Qvr,Qvϑ与Qvl分别为刚体平动与摆动以及钢丝绳弹性变形所对应的广义惯性力。
1.3 臂架系统多体动力学模型
回转作业时,吊臂系统与吊物系统通过球铰约束,吊臂系统各部件由于回转作业时无相互运动,采用自由度凝聚技术以减少模型计算量。对于整体臂架系统,通过引入臂头与钢丝绳上拉点的约束方程,可得臂架系统柔性多体动力学方程为
(12)
式中:M为总体质量矩阵;K为总体刚度矩阵;Q为外力列向量;QV为广义惯性力列向量,约束方程为
C(q,t)=R1(r0+xt+qft)-rt=0
(13)
式中:xt为臂头节点在吊臂浮动坐标系下的矢径;qft为臂头节点位移。
2 臂架动态特性试验检测
为考察臂架回转动态特性及验证模型的准确性,对回转作业时吊重的偏摆振动与主臂的动态应力进行了检测,要求试验环境为常温,无雨雪,风速<5 m/s。采用LMS动态应力测量系统对主臂在回转时的实时应力响应进行了测量,关注吊臂尾部臂节和中部臂节,检测系统采样频率为50 Hz,测量精度为±0.005 με。
基于GPS-RTK高精实时测量技术,对回转时吊重的偏摆特性进行了检测。检测系统如图4,现场测试见图5,该系统由1个基准站、4组移动站及相关数据采集与后处理设备构成,系统采样频率为10 Hz,精度为±5 mm。基准站放置于空旷地面并静止,用于各移动站精确位置坐标数据的修正。移动站1固接于基本臂,移动站2固接于臂头,移动站1、2所测数据用以确定WGS-84坐标系与当前臂头随动坐标系xsyszs的坐标转换系数,移动站3、4固接于吊钩两侧,通过移动站1、2所得实时坐标转换系数,可测吊钩在坐标系的实时空间位置坐标。进一步,吊重的侧向偏摆角αs和法向偏摆角βs表为

图4 偏摆振动检测系统

(14)

3 算列仿真
对建立的臂架系统动力学控制方程,利用New- mark方法实现方程的时域离散,采用Newton-Raphson迭代法对每一时间步进行非线性迭代求解。针对某型超大吨位轮式起重机,主要参数如表1, 臂架偏摆振动检测与动态应力检测回转速度时间历程曲线见图6。利用本文所构建的模型及传统的多刚体动力学模型进行了动态仿真分析,并与实测值进行了对比分析。
图7中描述了不同时刻下吊重钢丝绳的摆动特性,从图7(a)和(b)中可以看出,吊重侧偏角和正偏角呈波动趋势,且其波动周期相同。吊重侧偏角随时间振幅逐渐降低,但正偏角随时间振幅升高。本文所建立的柔性多体动力学方法所计算得到的偏摆角与实测值相比基本吻合,采用传统的多刚体动力学所得到的最大偏摆角与实测值相比偏差为32%,但采用本文算法所得结果与实测值相比只有6.8%,实测时,由于风激作用、相关发动机对臂架自身的自激振动等,吊重偏摆角初始时刻很难处于非完全静止状态,且相关激励伴随整个回转过程,而模型计算时忽略风的激振等,假设臂架从静止开始启动,相关扰动因素的忽略亦会导致二者的结果存在偏差。

表1 臂架系统相关结构参数

图6 起重机回转角速度时间历程
图8 为臂架不同测点处的动态应力演变图,可以看出,前55 s时臂架处于静止状态,但由于风载荷、以及吊重钢丝绳的轻微摆动,实测时臂架的应力很难达到稳态,而计算时假设臂架应力稳定,55~135 s为臂架回转时的应力响应,对于该测点,回转过程中应力振动规律与侧向偏摆角振动规律相近,吊重的侧向偏摆对吊臂应力波动影响显著,然臂架的侧向刚度低于回转法向刚度,为此机手操控及结构减振设计因尽量降低侧向振动。可以看出本文算法所得的计算结果与实测值吻合较好, 计算值与实测值回转过程中振动趋势相同,实测过程中,臂架迎风面较大,风激振动对吊臂应力响应有一定影响,仿真忽略风致激振的影响,导致二者计算结果存有偏差,且真实臂架系统各臂节间存在较小间隙,也会对臂架应力响应产生影响,中部测点如图8(b),计算值与实测值在启动阶段偏差稍大,但最大误差值在6%之内,总体而言,对于吊臂根部和中部测点,两者吻合较好,但对于吊臂其他处应力值的计算结果,还有待进一步验证分析。

(a) 侧向偏摆角

(b) 正向偏摆角

(a) 吊臂根部某点处应力响应

(b) 吊臂中部某点处的应力响应
4 结 论
(1) 针对超大吨位轮式起重机臂架系统,基于混合坐标系方法描述不同臂段、钢丝绳与吊重的刚体运动与变形振动,采用拉格朗日方程建立了臂架多体系统的刚柔耦合动力学方程,模型综合考虑了吊臂与吊重的惯性力效应、刚柔耦合效应以及吊臂的几何非线性效应。
(2) 通过对某超大吨位轮式起重机回转吊载动态仿真结果显示臂架动态性能呈现明显波动,吊重偏摆对吊臂应力波动有显著影响,与实测结果对比表明,本文所建立的计算方法所得的计算结果与实测值基本吻合,相比传统的多刚体算法,算法精度得到极大提升。
[1] 起重机设计规范:GB/T 3811—2008[S]. 北京: 中国标准出版社, 2008.
[2] WASFY T M, NOOR A K. Computational strategies for flexible multi body systems[J]. Appl Mech Rev, 2003, 56(6): 553-613.
[3] 张炜华,刘锦阳. 大变形复合材料薄板多体系统动力学建模[J].振动与冲击,2016, 35(8):27-35.
ZHANG Weihua, LIU Jinyang. Dynamic modeling of composite thin-plate multibody systems with large deformation[J]. Journal of Vibration and Shock, 2016, 35(8):27-35.
[4] SATO K,SAKAWA Y. Modelling and control of flexible rotary crane[J].International Journal of Control,1998,48: 2085-2105.
[5] 兰朋, 陆念力. 塔式起重机柔性臂回转制动过程动力分析[J]. 哈尔滨工业大学学报, 2004, 36(5): 677- 680.
LAN Peng, LU Nianli. Dynamic analysis of flexible jib of tower crane in case of braking slewing motion[J]. Journal of Harbin Institute of Technology, 2004, 36(5): 677- 680.
[6] 嘉红霞, 李万莉, SINGHOSE W. 考虑臂架弹性的动臂起重机动力学建模及振动分析[J]. 振动与冲击, 2010, 29(12): 136-140.
JIA Hongxia, LI Wanli, SINGHOSE W. Dynamic modeling and vibration analysis of cherry pickers with flexible arms[J]. Journal of Vibration and Shock, 2010, 29(12): 136-140.
[7] KU N, HA S. Dynamic response analysis of heavy load lifting operation in shipyard using multi-cranes[J]. Ocean Engineering, 2013, 83: 63-75.
[8] SOCHACKI W. The dynamic stability of a laboratory model of a truck crane[J]. Thin-Walled Structures, 2007, 45: 927-930.
[9] 黄毅,鄂加强,郭岗,等.超长柔性臂架回转振动主动控制研究[J]. 振动与冲击, 2016, 35(6):137-140.
HUANG Yi, E Jiaqiang, GUO Gang, et al. Active control of slewing vibration in an ultra-long flexible boom[J]. Journal of Vibration and Shock, 2016, 35(6):137-140.
[10] 刘锦阳, 洪嘉振. 刚-柔耦合动力学系统的建模理论研究[J].力学学报, 2002, 34(3): 408-415.
LIU Jinyang, HONG Jiazhen. Study on dynamic modeling theory of rigid-flexible coupling systems[J]. Chinese Journal of Theoretical and Applied Mechanics, 2002, 34(3): 408-415.
