K8型单层球面网壳爆炸动力响应的简化计算方法研究
2018-03-28苏倩倩翟希梅哈尔滨工业大学土木工程学院哈尔滨50090中冶建筑研究总院有限公司北京00088
苏倩倩, 翟希梅(.哈尔滨工业大学 土木工程学院,哈尔滨 50090;2.中冶建筑研究总院有限公司,北京 00088)
网壳结构在爆炸荷载下受力复杂,且多作为大跨空间公共建筑,一旦因爆炸而破坏乃至倒塌,将带来重大的生命财产损失。因此,有必要对该类结构的爆炸动力响应展开相关研究,以确保网壳结构在重大灾害中的安全并尽可能减少灾后损失。目前针对网壳结构的动力响应及抗爆性能的研究多局限于有限元数值模拟,如马加路等[1]基于网壳在爆炸荷载作用下的破坏及倒塌情况,提出了安全距离的计算方法。Zhai等[2-3]分析了不同炸药点位置、支撑条件以及屋面板厚度等参数下网壳在偏心爆炸荷载下的动力响应,并得到了结构的四种响应模式。高轩能等[4]研究了不同参数对单层球面钢网壳在内爆作用下动力响应的影响规律,并对柱壳结构的压力场进行了分析。田力等[5]研究了地下隧道内爆炸冲击作用下双层柱面网壳的动力响应。可见,众多学者都对爆炸荷载作用下网壳的动力响应以及防爆泄爆机理展开较多研究,但相关网壳的试验和理论研究尚处于空白。
鉴于大跨网壳结构复杂、体型庞大,其数值计算耗时巨大,且国内外缺少网壳结构的爆炸试验结果可对目前的爆炸数值响应模拟结果进行验证。因此,本文希望在网壳结构爆炸响应计算方法上探索新的方向,并为结构爆炸动力响应分析提供有效理论依据。根据哈密顿原理,以拉格朗日方程为基础[6-7],本文提出了一种适用于K8型单层球面网壳在爆轰荷载作用下动力响应求解的理论分析模型,并通过MATLAB求解微分方程组,进而得到结构动力响应。最后,将分别通过爆炸荷载下的简支梁及K8型单层球面网壳的响应结果与有限元结果的比较对本文方法的适应性进行验证。
1 简支梁爆炸动力响应的理论分析模型
本文采用三角形荷载来近似考虑爆炸荷载。首先以简支梁作为分析对象,计算结构在竖向均布爆炸荷载作用下的动态响应。简支梁模型如图1所示,跨度为2 m,截面为200 mm×200 mm的矩形。模型选用弹性钢材,密度为7 850 kg/m3,弹性模量为2.06×1011Pa,在简支梁上施加垂直于梁向下的均布线荷载p,p随时间的变化如图2所示。
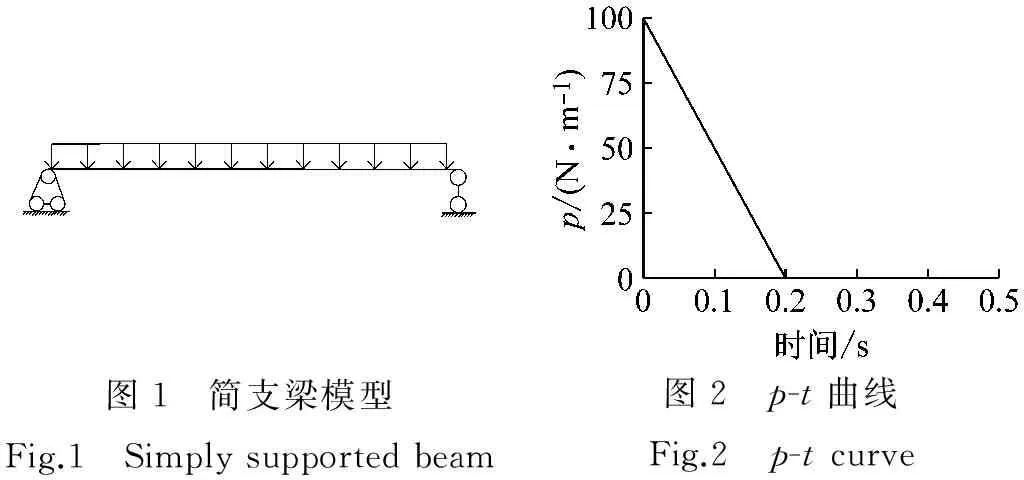
图1 简支梁模型Fig.1 Simplysupportedbeam图2 p-t曲线Fig.2 p-tcurve
通过求解式(1)所示的拉格朗日平衡方程,可获得简支梁在三角形荷载作用下的动力响应
(1)
其中:V=∑U+PE=Um+Ub+PE
式中:Ci(t)为广义位移;T为动能;V为总势能;Um为轴向变形能;Ub为弯曲变形能;PE为势能损失量。
简支梁的变形方程取正弦函数的叠加,为了不让计算过于复杂,取两个正弦函数进行叠加,如式(2)所示。变形函数的选取,要满足边界条件,w(0,t)=0,w(l,t)=0。
(2)
式中:w(l,t)指节点的竖向变形量;L指梁长;l指梁长的变量,从0到L代表从简支梁的左端到右端。
根据变形函数,可以得到简支梁每个点的竖向变形,根据式(3)计算出梁的弯曲变形能
(3)
式中:E为弹性模量;I为杆件截面惯性矩。由于简支梁在竖向荷载作用下没有轴向变形,所以轴向变形能为零,简支梁的内能就是弯曲变形能。
根据变形函数可以得到简支梁上每点的速度如式(4)所示
(4)

(5)
式中:ρ为密度;A为截面面积。
势能损失量PE可根据式(6)进行计算,其中,荷载p为均布线荷载,垂直向下作用于梁

(6)
计算出简支梁的内能、动能和势能损失量,代入式(1)所示的拉格朗日方程,并通过MATLAB编程求解该微分方程组的数值解。令l=L/2,可以得到简支梁中点的位移响应,进而计算得到简支梁内能和动能时程。
下面,对上述简支梁模型进行有限元分析,采用LS-DYNA动力分析软件建立相应有限元模型,简支梁采用BEAM161单元,均布线荷载p垂直于梁向下。
经有限元分析,获得各个峰值位移时刻简支梁的竖向变形如图3所示(变形放大10倍)。将有限元模拟与基于拉格朗日动力方程的理论分析模型MATLAB计算得到的简支梁中点位移时程、简支梁系统动能和总内能(弯曲变形能)结果对比如图4和表1所示。

(a) t=0.041 s

(b) t=0.086 s

(c) t=0.127 s

(d) t=0.172 s

(e) t=0.214 s

(f) t=0.257 s
Fig.3 Deformation of simply supported beam (10 times amplified)
从图4和表1可以看出,有限元分析与基于拉格朗日方法理论分析模型计算得到的简支梁中点振动规律、峰值位移以及系统的动能、总内能都极为接近。简支梁中点的位移响应按照正弦形式振荡,在0.04 s左右达到峰值位移,之后节点位移衰减到负值再回到正值,峰值位移一直在减小,0.2 s后由于没有荷载作用,节点在平衡位置附近上下振动。由于未考虑阻尼,0.2 s后没有衰减,以固定的峰值位移一直振动下去,且简支梁系统的动能和内能峰值也都不再发生变化。经计算,简支梁中点正向位移峰值误差仅为0.37%,可见采用该理论分析模型来近似计算结构在爆炸荷载作用下的动力响应是可行的。

(a) 中点位移时程曲线
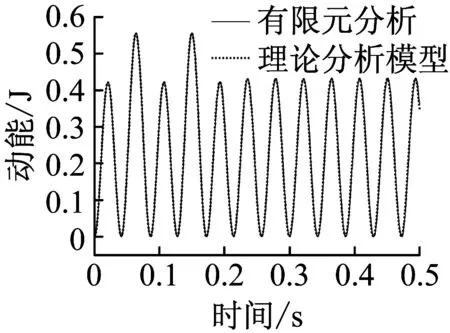
(b) 动能时程曲线
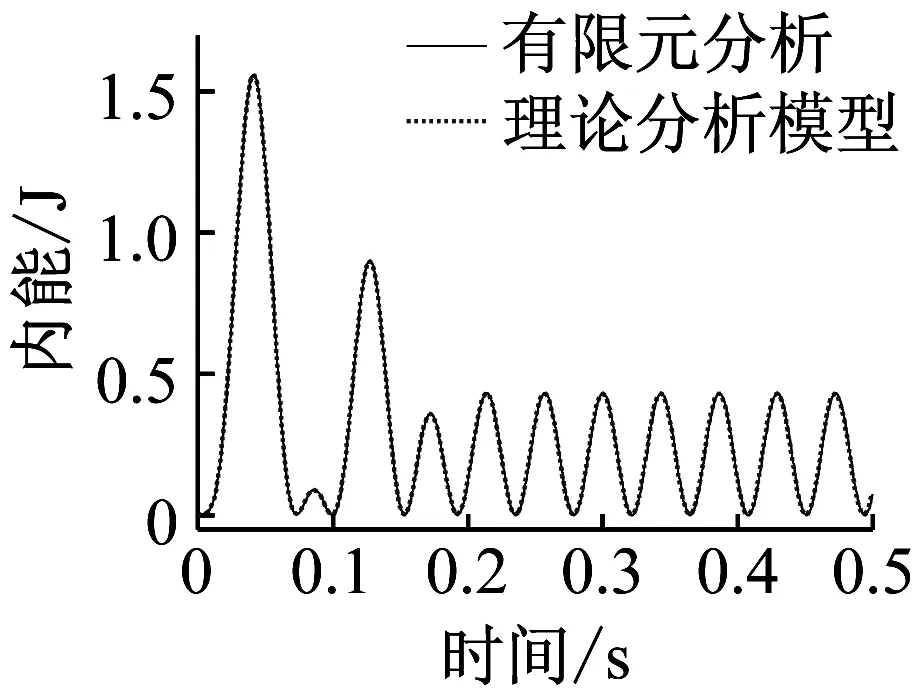
(c) 内能时程曲线

动力响应正向峰值/m与有限元误差值/%负向峰值/m与有限元误差值/%中点位移有限元模拟0.0136400.007210理论计算0.01359-0.370.00717-0.55动能有限元模拟0.5563000理论计算0.5563000内能有限元模拟1.5603000理论计算1.56120.0600
2 K8型网壳基于拉格朗日方法动力响应计算
下面,我们将基于拉格朗日方法的理论分析模型应用到K8型单层球面网壳结构,由于网壳结构比较复杂,杆件较多,本文暂时仅考虑网壳杆件,并选取分频数为2的K8型单层球面网壳进行计算分析。根据变形函数中广义位移参数的个数,本节分为两参数分析、三参数分析以及改进后的三参数分析。
2.1 爆炸荷载作用下K8型网壳动力响应两参数分析模型
模型为分频数为2的K8型单层球面网壳杆件,跨度为5 m、矢跨比为1/5,主杆采用Φ14×0.5 mm圆钢管,网壳底部节点采用固定约束,模型如图5所示。模型选用弹性钢材材料,参数设置同第1节。
在网壳的每个顶点上施加集中荷载P(t),P(t)为简化爆炸荷载——三角形荷载,P(t)随时间的变化如图6所示,在t=0时刻P0为荷载峰值,荷载P(t)的方向沿径向向外,荷载施加方式见图5。

(a) 轴侧图

(b) 正视图
由于网壳模型以及三角形荷载的对称性,本文取1/8模型进行理论分析计算,这样可以很大程度的减少计算量和编程量,理论分析模型如图7所示。图中,1~6表示网壳节点,L1~L6表示网壳杆件。
从网壳结构整体变形方面假设网壳的变形函数,如式(7)所示。通过变形函数可以确定6个节点的变形。由于该变形函数中有两个待求解广义位移参数,因此本节为两参数分析。变形函数满足边界条件,w(0,t)=0
(7)
式中:w(l,t)指节点的径向变形量;L指弧长;l指弧长的变量,从0到L,代表从网壳边缘到顶点。

图6 P-t曲线Fig.6 P-tcurve图7 理论分析模型Fig.7 Theoreticalanalysismodel
根据变形函数,求得网壳6个节点的径向变形量,然后计算出9根杆件变形后的长度以及变形量Δi。继而根据式(8)可以求得9根杆件的轴向变形能之和,Um是关于广义位移Ci(t)的函数
(8)
式中:Lbi指每根杆件变形前的长度。网壳6个节点相应的速度可由式(9)求得
(9)

(10)
求解过程中,对称截面位置处杆件的截面取Φ7×0.5 mm圆钢管,其他杆件截面为Φ14×0.5 mm圆钢管。
势能损失量PE可根据式(11)进行计算,由于模型的对称性,作用在1点的荷载为P(t)/8,作用在2点和3点的荷载为P(t)/2。
PE=-∑P(t)×w(l,t)
(11)
计算出网壳的内能、动能和势能损失量,代入式(1)所示的拉格朗日方程,通过MATLAB编程求解,即可得到结构6个节点的位移响应,进而计算得到网壳结构的内能和动能时程。
2.2 爆炸荷载作用下K8型网壳动力响应三参数分析模型
本节在2.1节中网壳整体变形函数(式(7))的基础上,再假设每根杆件的变形如式(12)所示。这样,本节分析中,变形函数中共有三个待求解广义位移参数,称为三参数分析。
(12)

每根杆件变形后的长度由两部分组成,第一部分是由于节点径向位移w(l,t)导致的杆件变形量,该部分就是2.1节中杆件变形后的长度,第二部分是由于杆件弯曲导致的变形量,由变形函数wb(x,t)以及以直代曲的近似计算方法,可以得到每根杆件的变形量如式(13)所示。继而根据式(8)可以得到9根杆件的轴向变形能之和。杆件的弯曲变形能由式(14)计算。
(13)
(14)
网壳6个节点相应的速度如式(9)所示,网壳杆件上任一点的速度由两部分组成,第一部分是由于网壳节点运动导致的杆件上线性分布的速度,这一部分同2.1节,第二部分是由于杆件发生弯曲变形导致的速度,可以由式(15)计算得到,将这两部分速度叠加,即可得到网壳杆件上任意一点的速度。然后根据式(10)可以计算9根杆件的动能之和。
(15)
势能损失量PE同2.1节一样,将网壳的内能、动能和势能损失量代入式(1)所示的拉格朗日方程,并通过MATLAB编程求解,即可得到结构6个节点的位移响应,进而计算得到网壳结构的内能和动能时程。
2.3 K8型网壳理论计算与有限元结果的对比分析
为了与基于拉格朗日动力方程的理论分析结果对比,本节采用LS-DYNA软件建立了一个与理论计算模型相对应的K8型单层球面网壳1/4模型,主杆采用Φ14×0.5 mm圆钢管,对称截面处采用Φ7×0.5 mm圆钢管,采用BEAM161单元。有限元模型如图8所示。

(a) 俯视图

(b) 正视图
钢材选用弹性材料,参数设置同第1节。在网壳顶点及第一环的三个顶点上施加集中荷载,由于模型的对称性,作用在1点的荷载为P(t)/4,作用在2点的荷载为P(t),作用在22点和42点的荷载为P(t)/2。P(t)随时间的变化同2.1节。
约束模型底部5个节点的三向位移、对节点1和22施加Y轴对称约束、对节点1和42施加X轴对称约束,不同荷载下的响应结果皆显示:X向和Y向位移较小且数值接近,两者的位移峰值响应仅为Z向位移响应的28.36%,表明位移响应是以Z向为主,因此本文后续分析中仅给出Z向位移响应结果。当荷载峰值P0为50 kN时,提取K8型球面网壳结构在不同时刻的Z向位移如图9所示。
从图9可以看出,三角形爆炸荷载作用下网壳结构的位移响应受高阶振型影响非常大,这是由网壳自身结构特性决定的。同时,网壳杆件上节点相较于杆件与杆件的交点来说,位移响应有滞后的效应。网壳底部杆件发生响应的时间最迟,且位移响应较小。
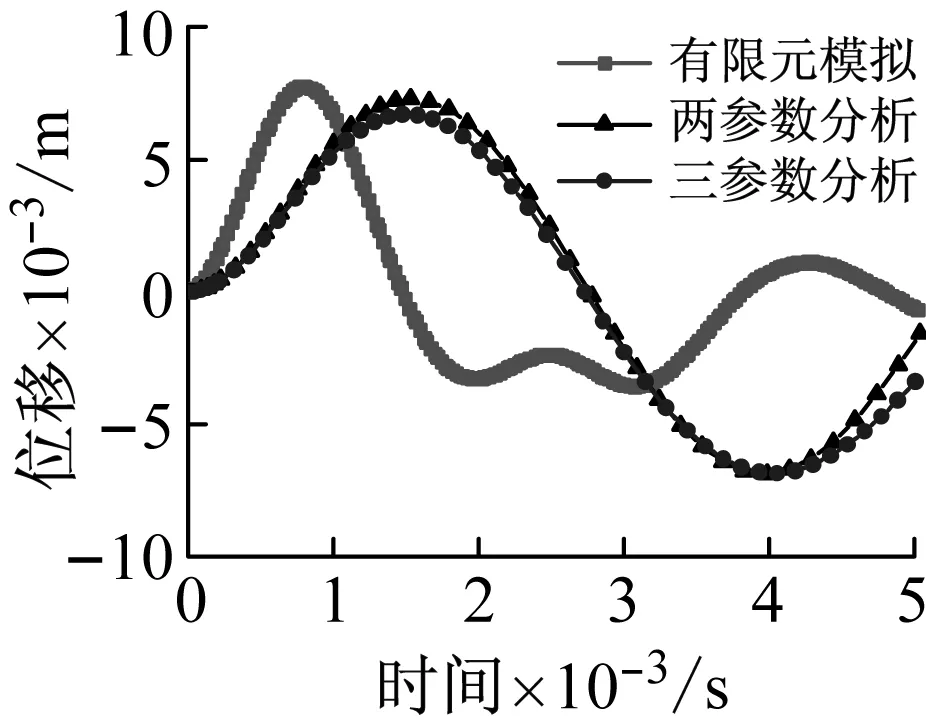
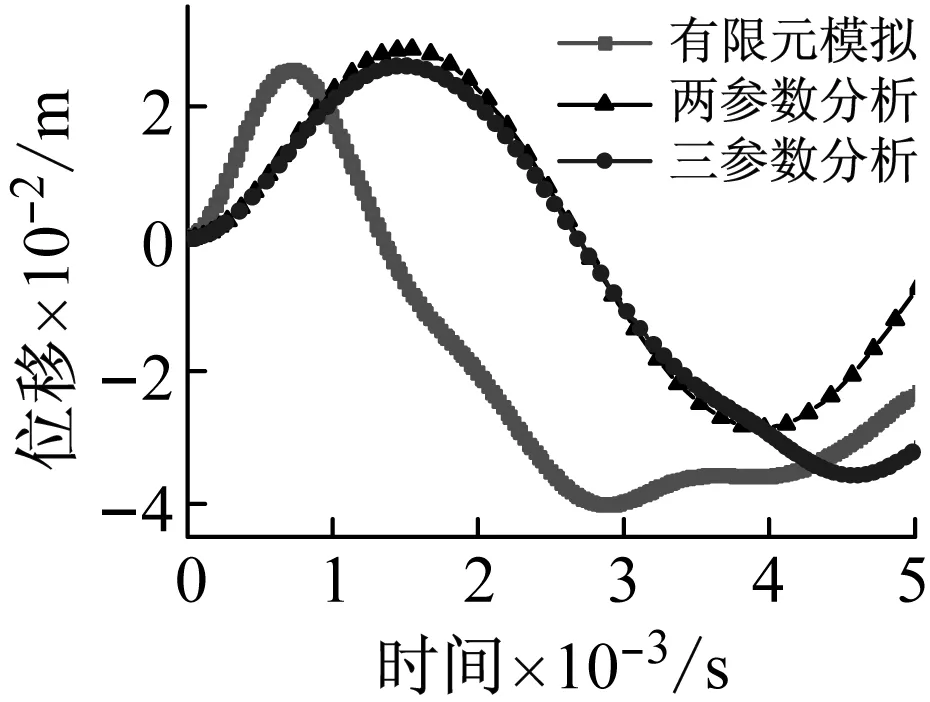
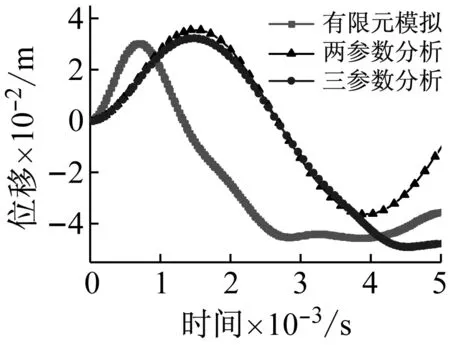
荷载峰值P0分别为10 kN、20 kN、30 kN、40 kN、50 kN时,将有限元数值分析、基于拉格朗日方程的理论两参数和三参数分析得到的网壳最大节点位移(Z向)时程对比如图10所示。

(a) t=0.000 25 s

(b) t=0.000 5 s

(c) t=0.000 75 s
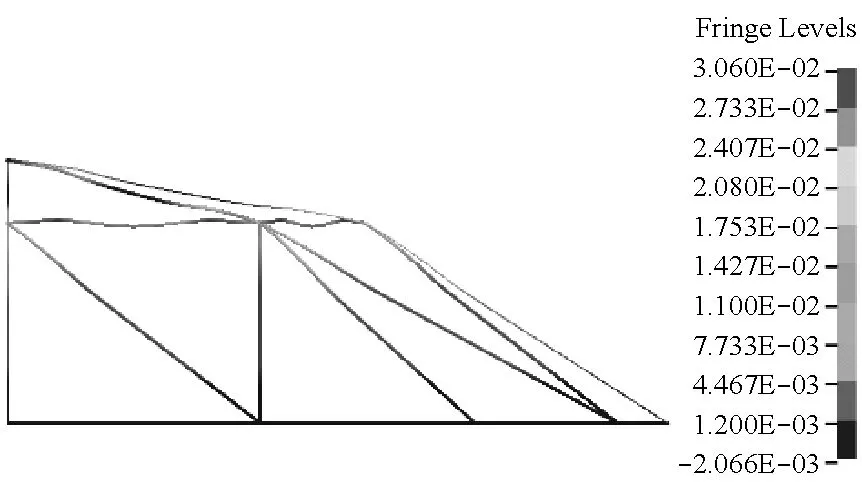
(d) t=0.001 s

(e) t=0.001 5 s

(f) t=0.002 s
Fig.9Z-displacement of K8 single-layer reticulated shell(P0=50 kN)
(a) P0=10 kN

(b) P0=20 kN

(c) P0=30 kN
(d) P0=40 kN
(e) P0=50 kN
从图10可以看出,两参数和三参数理论分析模型得到的最大位移节点按照正弦形式振荡,节点都在0.001 5 s左右达到正向峰值位移,然后开始衰减,经过平衡位置后负向位移逐渐增大,并且三参数分析中节点再次回到平衡位置的时间要比两参数分析滞后,荷载峰值P0越大,这种规律越明显。当荷载峰值P0从10 kN增大到50 kN时,有限元数值模拟与基于拉格朗日动力方程计算得到的网壳最大位移节点时程(Z向)的正向峰值位移对应较好,但理论分析达到正向峰值位移的时刻比有限元分析滞后一倍左右。同时,基于拉格朗日动力方程两参数计算得到的位移响应比三参数计算结果偏大,这是因为两参数计算过程中没有考虑杆件的弯曲,外力功仅转变为轴向变形能和动能,而三参数计算过程中外力功转变为轴向变形能、弯曲变形能和动能。
对比前1-2个振动周期,基于拉格朗日动力方程的理论分析模型和有限元产生误差的原因有:①由于网壳结构自身特性,高阶振型影响非常大,而理论分析模型中假设的变形函数比较简单,最多考虑前三阶振型,且该变形函数和有限元的变形模式有偏差,不能完全相符;②有限元分析中,三角形爆炸荷载作用下网壳杆件上节点相较于杆件与杆件的交点来说,位移响应有滞后的效应,而理论分析模型中假设变形函数时,是以杆件交点与杆件同时达到峰值位移进行计算的;③MATLAB求解拉格朗日方程过程中,采用数值解,有累计的数值求解误差。
其中,第一个和第二个原因最关键,第二个原因也是导致理论分析模型两参数和三参数分析结果相差较小的主要原因。可以通过增加理论分析模型变形函数中的参数个数以及单独假设每根杆件的变形函数来改善,但这样将导致MATLAB编程量大幅度增加。
2.4 爆炸荷载下K8型网壳动力响应计算方法的修正
根据2.3节中基于拉格朗日动力方程理论分析与有限元分析产生误差的原因,对2.2节中的理论分析模型进行改进,改进方法介绍如下。
有限元模型中,网壳结构的最大位移节点(2点)几乎都在0.000 7 s左右达到峰值,当荷载峰值P0为30 kN时,在0.000 738 s达到最大位移0.020 3 m,针对该算例,提取t=0.000 738 s时刻节点1和节点2之间杆件节点、节点2和节点101之间杆件节点的Z向位移如图11所示。为了更直观的将变形曲线表达清晰,绘制时将位移放大10倍。

图11 杆件变形图
从图11可以看出,上部杆件的变形接近1/2周期的三角函数,下部杆件的变形接近1/4周期的三角函数,于是,在网壳杆件交点变形函数(式(7))的基础上,对2.2节中杆件的变形函数进行修正。其中,理论分析模型中杆件编号见图7所示。
杆件1、杆件2和杆件5的变形函数取式(16),杆件3、杆件6、杆件7和杆件4的变形函数取式(17)。
(16)
(17)
根据变形函数,先由2.1节中整体变形函数得到网壳节点变形后的坐标以及杆件变形后长度,再以直代曲的近似计算方法,杆件1、杆件2和杆件5的最终变形量由式(18)计算,杆件3、杆件6、杆件7和杆件4的最终变形量由式(19)计算,进而根据式(8)计算所有杆件轴向变形能之和。
(18)
(19)
杆件1、杆件2和杆件5的弯曲变形能由式(20)计算,杆件3、杆件6、杆件7和杆件4的弯曲变形能由式(21)计算,杆件8和杆件9弯曲变形能为零。
(20)
(21)
同2.2节一样,网壳杆件上任一点的速度由两部分组成,其中,杆件1、杆件2和杆件5任意一点由弯曲导致的速度由式(22)计算,杆件3、杆件6、杆件7和杆件4任意一点由弯曲导致的速度由式(23)计算。然后根据式(10)可以计算9根杆件的动能之和。
(22)
(23)
势能损失量PE同2.1节一致,计算出网壳的内能、动能和势能损失量,代入式(1)所示的拉格朗日方程,并通过MATLAB编程求解,即可得到结构6个节点的位移响应,进而计算得到结构的内能和动能时程。
当荷载峰值P0分别为10 kN、20 kN、30 kN、40 kN、50 kN时,将有限元分析、基于拉格朗日方程的理论三参数分析以及改进后的三参数分析得到的网壳最大节点位移(Z向)时程对比如图12所示,数值见表2。
从图12可以看出,改进后的三参数分析得到的网壳的最大节点位移(Z向)时程与有限元分析更为接近。并且,荷载峰值P0越大,误差越小,尤其是负向峰值位移和达到负向峰值位移的时间与有限元结果更为贴近。
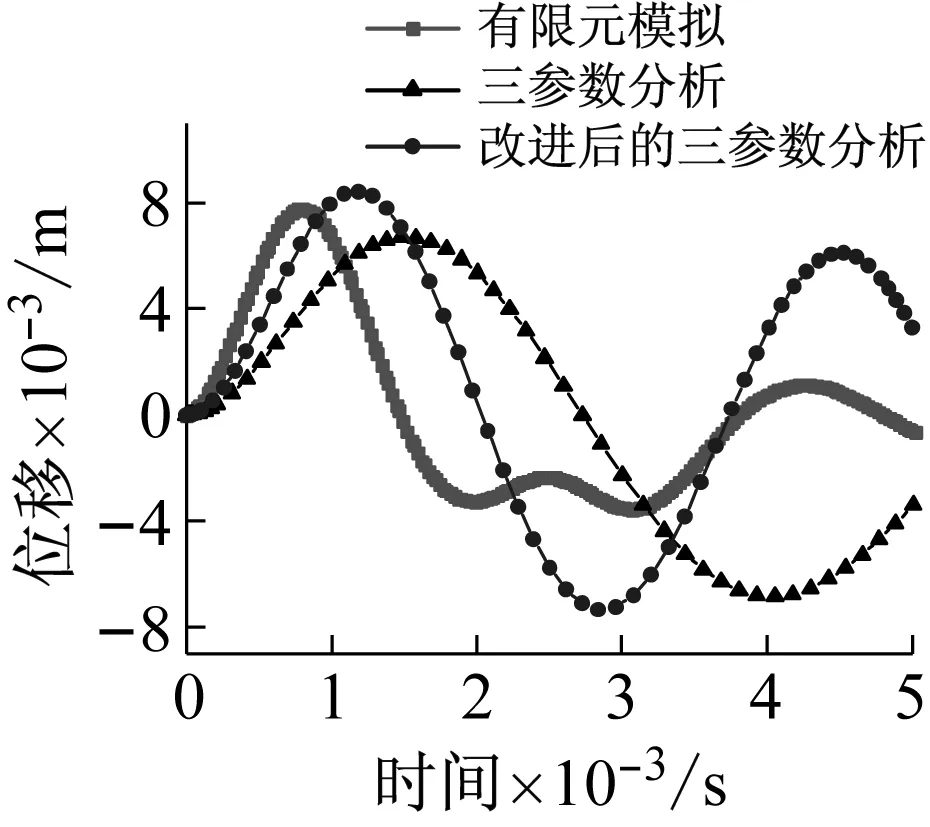
(a) P0=10 kN
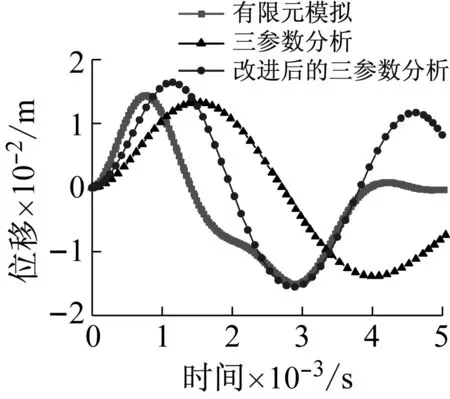
(b) P0=20 kN
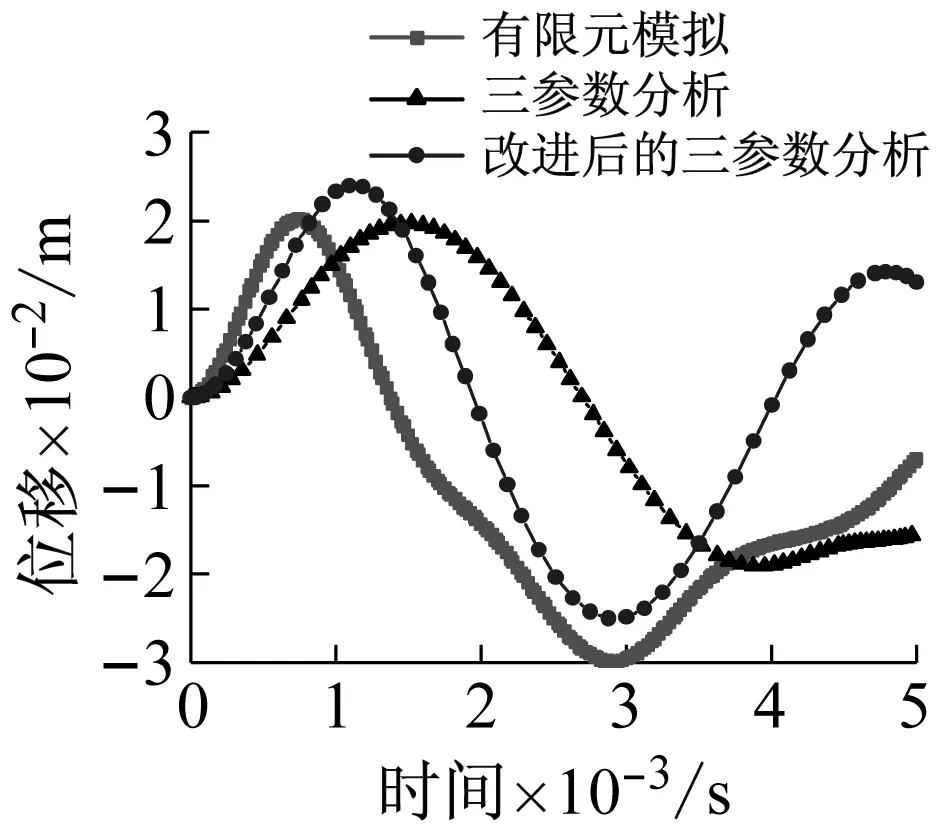
(c) P0=30 kN

(d) P0=40 kN
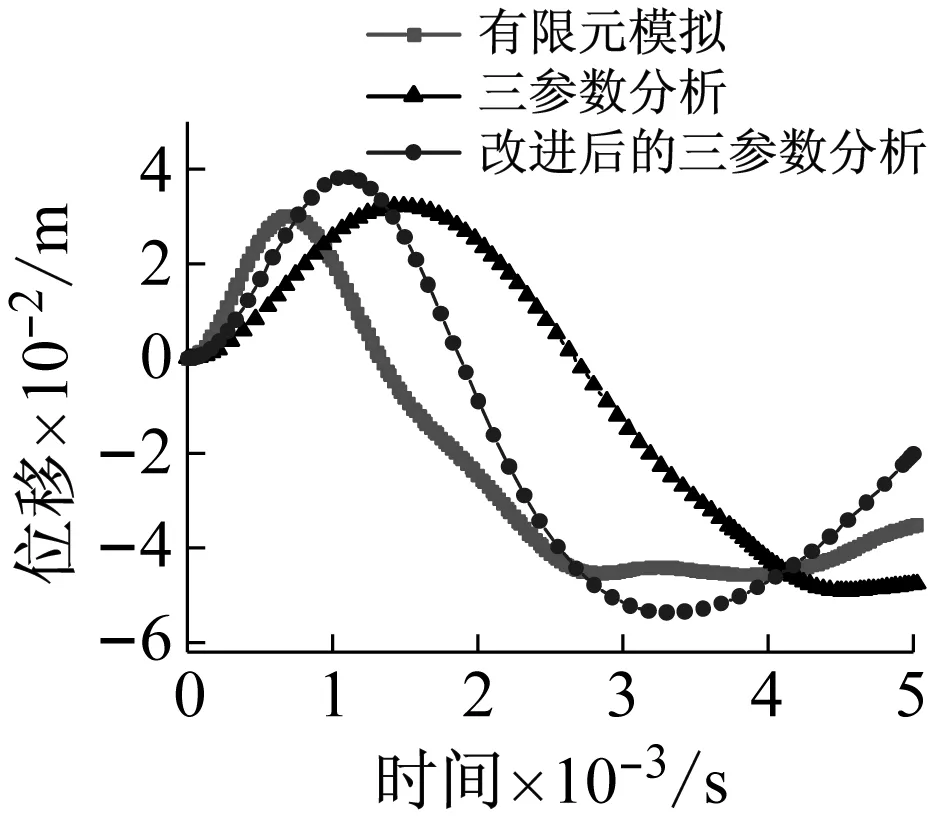
(e) P0=50 kN
从表2可以看出,当荷载峰值P0从10 kN增大到30 kN时,原三参数分析得到的正向峰值位移值均比有限元分析结果要小,当P0为40 kN和50 kN时,则反之。而改进后的三参数分析结果均比有限元分析结果偏大,最大误差为26.8%。除了当P0为10 kN时,负向峰值位移误差较大,其他4组荷载下,负向峰值位移都吻合较好,原三参数分析最大误差为35.9%,改进后的三参数分析最大误差为16.1%。
综合图12和表2,本文认为改进后的三参数理论分析模型得到的网壳最大节点位移(Z向)振动规律比原三参数分析更贴合有限元分析结果。
将有限元分析、基于拉格朗日方程的理论三参数分析以及改进后的三参数分析得到的网壳系统动能、内能时程对比分别如图13和图14所示。
从图13可以看出,改进后的三参数分析得到的网壳结构的动能时程以及达到动能峰值的时刻与有限元结果的振动规律更为接近,理论分析得到的总动能最大值均出现在时程的第二个峰值,有限元的总动能最大值出现在时程的第二个或第三个峰值。

表2 网壳位移响应对比

(a)P0=10kN(b)P0=20kN(c)P0=30kN(d)P0=40kN
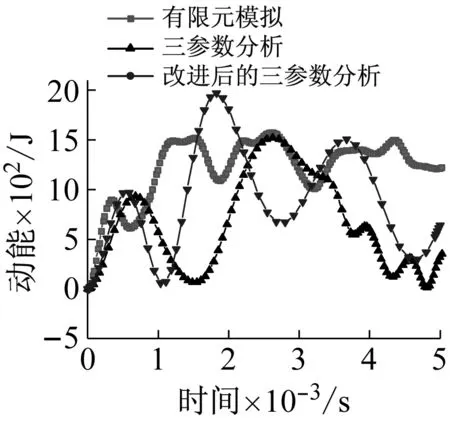
(e) P0=50 kN
从图14可以看出,改进后的三参数理论分析模型得到的内能峰值、达到内能峰值所用的时间均比原三参数分析结果更接近有限元分析,当荷载峰值P0为30 kN和40 kN时,改进后的三参数理论分析得到的内能最大值与有限元分析结果误差最小。

(a) P0=10 kN
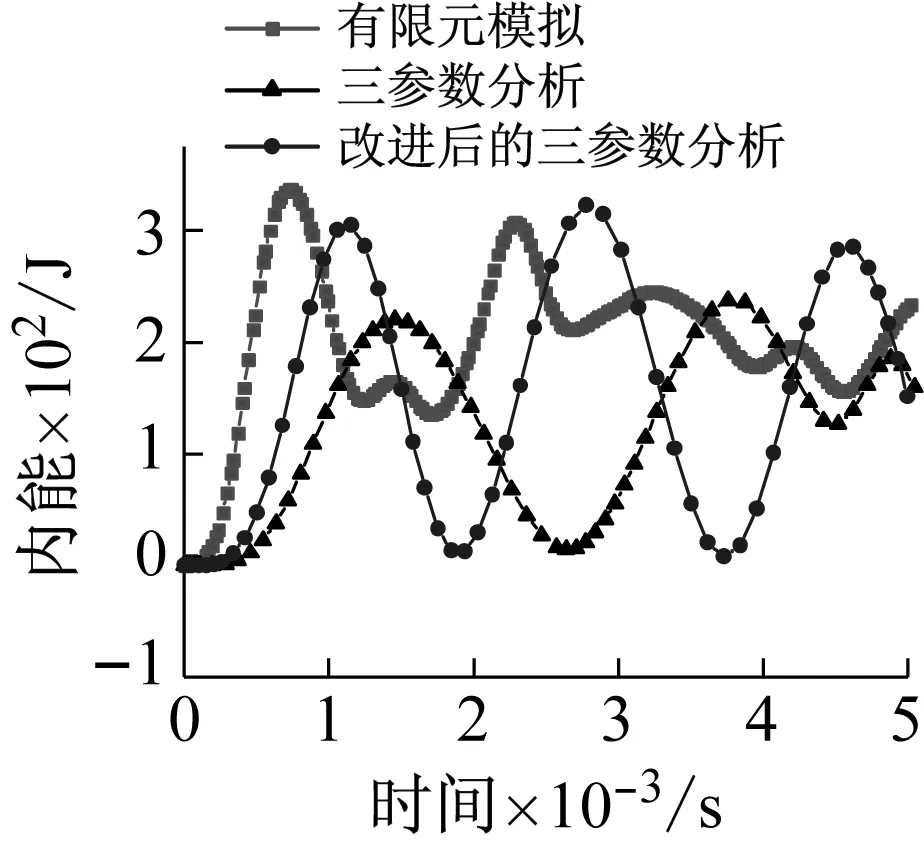
(b) P0=20 kN

(c) P0=30 kN

(d) P0=40 kN
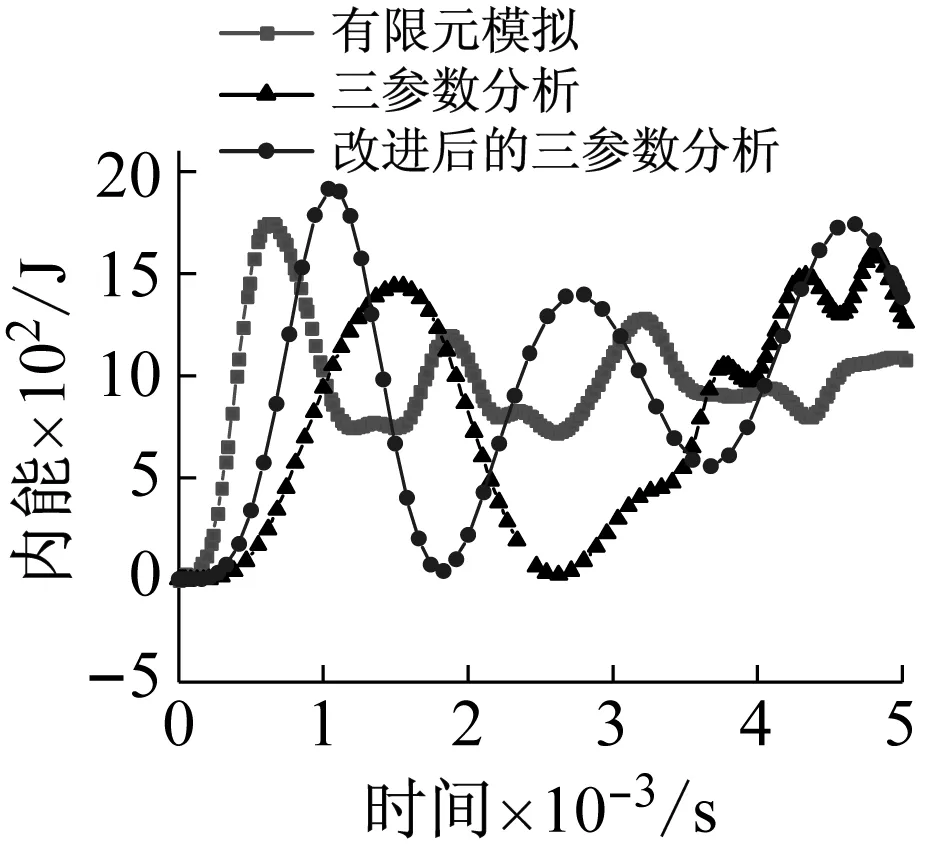
(e) P0=50 kN
综合考虑最大节点位移响应、网壳结构的动能和内能情况,建议采用基于拉格朗日动力方程的理论分析模型计算网壳在爆炸荷载作用下的动力响应时,荷载峰值P0不小于20 kN。
3 结 论
本文以拉格朗日动力方程为基础,提出一种适用于简支梁和K8型单层球面网壳在简化爆炸荷载作用下动力响应的计算方法,并与LS-DYNA有限元分析结果进行对比和误差分析,得到以下结论:
(1) 利用该方法获得的简支梁在三角形爆炸荷载作用下的跨中振动规律、峰值位移、速度以及系统的动能和内能等与有限元结果十分吻合,其中最大节点位移峰值误差仅为0.37%。
(2) 当荷载峰值P0从10 kN增大到50 kN时,有限元数值模拟与基于拉格朗日动力方程计算得到的网壳最大位移节点时程(Z向)的正向峰值位移对应较好,但理论分析达到正向峰值位移的时刻比有限元分析滞后一倍左右。
(3) 改进后三参数分析模型得到的最大节点位移(Z向)时程、网壳结构的总动能和总内能与有限元分析结果更为接近。建议如采用该理论分析模型计算网壳动力响应时,荷载峰值P0应不小于20 kN,且假设的变形函数应接近网壳实际变形。
[1] 马加路,支旭东,范峰,等. 外爆荷载下Kiewitt8型单层球面网壳的动力响应[J]. 振动与冲击, 2015,34(21):65-70.
MA Jialu, ZHI Xudong, FAN Feng, et al. Dynamic responses of Kiewitt 8 single-layer reticulated domes subjected to outside explosion loads[J]. Journal of Vibration and Shock, 2015,34(21):65-70.
[2] ZHAI Ximei, WANG Yonghui, HUANG Ming. Performance and protection approach of single-layer reticulated dome subjected to blast loading[J]. Thin-Walled Structures, 2013,73:57-67.
[3] 翟希梅,黄明. 偏心爆炸荷载下网壳结构的动力响应分析[J]. 振动与冲击. 2014,33(4):178-184.
ZHAI Ximei, HUANG Ming. Dynamic response of a reticulated shell under eccentric blast loading[J]. Journal of Vibration and Shock, 2014,33(4): 178-184.
[4] 高轩能,李超,江媛. 单层球面钢网壳结构在内爆炸作用下的动力响应[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(增刊1):102-109.
GAO Xuanneng, LI Chao, JIANG Yuan. Dynamic responses of single-layer spherical steel reticulated shell under internal explosions[J]. Journal of Tianjin University (Science and Technology), 2015,48 (Suppl):102-109.
[5] 田力,李灵聚. 双层柱面网壳结构在地下隧道内爆炸冲击下的动力响应分析[J]. 振动工程学报, 2011, 24(5):482-490.
TIAN Li, LI Lingju. Dynamic response analysis of the cylindrical reticulated shell structure due to an underground in-tunnel explosion[J]. Journal of Vibration Engineering, 2011, 24(5):482-490.
[6] SCHLEYER G K, HSU S S. A modelling scheme for predicting the response of elastic-plastic structures to pulse pressure loading[J]. International Journal of Impact Engineering, 2000(24):759-777.
[7] DONALDSON B K. Introduction to structural dynamics[M]. Cambridge: Cambridge University Press, 2012: 46-70.
