星载串联型柔性抓捕机构的多级阻尼镇定控制
2018-03-28董正宏任珊珊贾庆轩北京邮电大学自动化学院北京100876空间机器人技术教育部工程研究中心北京100876航天工程大学科研学术处北京101416
褚 明, 董正宏, 任珊珊, 贾庆轩(1. 北京邮电大学 自动化学院,北京 100876; 2. 空间机器人技术教育部工程研究中心,北京 100876; . 航天工程大学 科研学术处,北京 101416)
在轨捕获是开展在轨维修、装配及碎片清除等空间任务的重要环节。利用星载抓捕机构与目标航天器对接时,瞬时碰撞力产生的脉冲式动量易引起漂浮基座的姿态倾斜和角动量超限,且抓捕机构的传动关节处会产生冲击振动,该类动力学响应使得捕获后的系统产生扰动,严重时可导致失稳。因此,最大程度地减小碰撞动量对漂浮基座的扰动,且快速衰减抓捕机构传动关节处的振动,成为在轨捕获的关键技术之一。近年来,利用串联型多自由度机械臂开展在轨捕获成为该领域的热点课题,国内外诸多学者研究了通过星载机械臂完成在轨捕获过程的动力学分析和镇定控制方法。Xu等[1]讨论了柔性冗余机械臂的运动学冗余特性,通过机械臂的预构型方法缓解在轨捕获引起的振动和冲击。丛佩超等[2]提出直臂抓取的概念,基于机械臂动量守恒提出碰撞前的配置规划方法,以减小耦合角动量并实现稳定捕获。Wei等[3]提出一种动态抓取域方法来减小振动冲击,从而消除碰撞冲量对漂浮基座的扰动影响。Liu等[4]对捕获后的柔性机械臂进行动力学建模,采用PD控制器实现捕获碰撞后系统的快速稳定。Dong等[5-6]针对双关节漂浮基柔性空间机械臂在轨捕获卫星过程的接触、碰撞动力学建模和碰撞后混合体系统镇定运动控制及柔性振动主动抑制问题进行了研究。利用阻尼力实现柔性机构的振动抑制是主动控制的重要方法之一[7-9],磁流变阻尼器[10]具有阻尼力可控和响应快速的特征,在振动控制领域应用广泛。Nguyen等[11]将阻尼可控的磁流变阻尼器用于空间捕获的平面二自由度机械臂模型,定性验证了带有反馈比例控制器的阻尼器可以有效抑制旋转目标的角动量,减小碰撞对系统的影响,但其成果仅局限于少自由度模型和阻尼力的开关控制,未解决多自由度模型下多级可控阻尼的优化控制问题。
本文基于十字轴结构的软接触关节装置[12],提出一种具有多级可控阻尼的串联型柔性抓捕机构广义模型,通过在关节处引入多维可控阻尼器,再由多个关节和连杆组成多自由度串联机构,能实现对空间任意方向碰撞动量的缓冲和卸载。采用Kane方法建立漂浮基座耦合柔性抓捕机构的一体化动力学方程,利用微粒群寻优算法实现多级最优阻尼力的求解,实现了捕获后不稳定系统的镇定控制。最后,对提出的镇定控制方法进行数值仿真和性能对比,结果表明,微粒群优化控制方法能有效消除碰撞力对漂浮基座的扰动,保证基座姿态稳定的同时抑制了柔性抓捕机构的振动。
1 具有多级阻尼的柔性抓捕机构模型
提出一种具有多级可控阻尼的N(N为自然数)关节柔性抓捕机构模型,如图1所示。Oxyz为惯性坐标系,Oixiyizi(i=1,2,3,…,N+1)顺次为漂浮基座和刚性连杆端面处的连体坐标系,在每个连杆的端面连体坐标系处为连接各个连杆的关节。关节处设置可控阻尼器件,以第j个端面连体坐标系为例(j=2,3,…),分别沿Ojxj、Ojyj、Ojzj三个坐标轴的直线方向设置三个直线阻尼器,用于镇定沿该三个坐标轴直线方向的碰撞动量;分别绕Oixi、Oiyi、Oizi三个坐标轴旋转方向设置三个旋转阻尼器,用于镇定绕该三个坐标轴旋转方向的碰撞动量,故每个关节均可对空间六维方向的碰撞动量实现镇定。通过N个连杆将关节进行串联,可组成具有6N自由度的多级阻尼柔性抓捕机构。

图1 具有多级阻尼的串联型柔性抓捕机构模型
2 动力学方程
由于阻尼器具有一定的刚度系数和阻尼系数,因此,每个关节可简化为6个弹簧模型和6个阻尼模型,则N关节柔性抓捕机构可离散为由6N个弹簧和6N个阻尼连接的多刚体段模型。若将漂浮基座视为具有6个自由度的虚拟连杆,则带有漂浮基座的N关节柔性抓捕机构可等效为具有(6N+6)个自由度的固定基座系统。采用Kane方法对带有漂浮基座的N关节柔性抓捕机构进行一体化动力学建模,可得到柔性抓捕机构捕获后动力系统的广义微分方程。
2.1 变换矩阵


(1)

(2)
Okxkykzk相对于惯性系Oxyz的绝对变换矩阵
(3)

则任意刚体段的运动学方程
(4)
式中:c=cos,s=sin。
2.2 偏角速度和偏线速度
惯性坐标系中,第k段的角速度
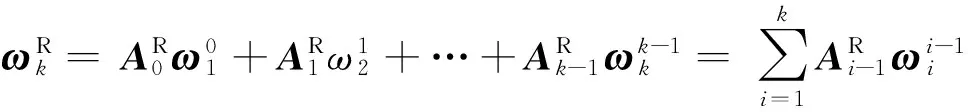
(5)
则偏角速度
(6)
用矩阵Wkl存储刚体k对广义速度yl的偏角速度
(7)
式中:l=1, 2, 3, …, 6N+6。
刚体k的质心在惯性系下的位置矢量

(8)
式中:pRO为坐标系O1x1y1z1在惯性系中的位置矢量;di为第i段刚体在坐标系Oixiyizi中的位置矢量;rk为第k段刚体的质心在坐标系Okxkykzk中的位置矢量。
将式(8)对时间求导,得到第k段刚体的质心在惯性系中的速度
(9)
则偏线速度
(10)
将式(9)代入式(10)得到刚体k对广义速度yl的偏线速度

(11)
2.3 等效主动力(矩)及等效惯性力(矩)
忽略重力,以第k段刚体为例进行受力分析,第k段所受的主动力包括:左侧有3个直线阻尼器的弹性变形力Fkz、3个旋转阻尼器的弹性变形力矩Mkz、3个直线阻尼器的阻尼力Fukz、3个旋转阻尼器的阻尼力矩Mukz,右侧有3个直线阻尼器的弹性变形力Fky、3个旋转阻尼器的弹性变形力矩Mky。
根据坐标变换矩阵及弹性变形力得到第k段刚体左右两侧阻尼器的弹性变形力
·diag(K1,K2,K3,K4)
(12)
式中:Fkz为第k段左侧受到的弹性变形力;Mkz为第k段左侧受到的弹性变形力矩;Fkv为第k段右侧受到的弹性变形力;Mkv为第k段右侧受到的弹性变形力矩;K1为左侧直线阻尼器的弹性系数;K2为左侧旋转阻尼器的弹性系数;K3为右侧直线阻尼器的弹性系数;K4为右侧旋转阻尼器的弹性系数。
各段质心所受的等效主动力Fkc和主动力矩Mkc为
(1) 基座(k=1)
漂浮基座左侧没有关节,仅受右侧关节1 的作用力
(13)
式中:r1为基座质心到连体坐标系原点的距离。
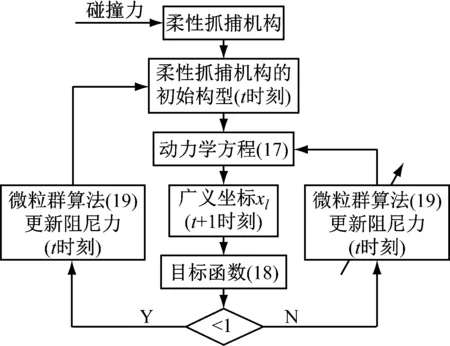
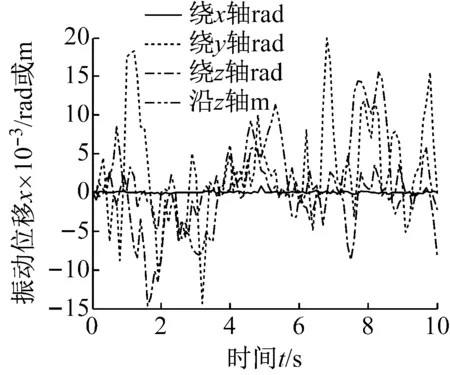
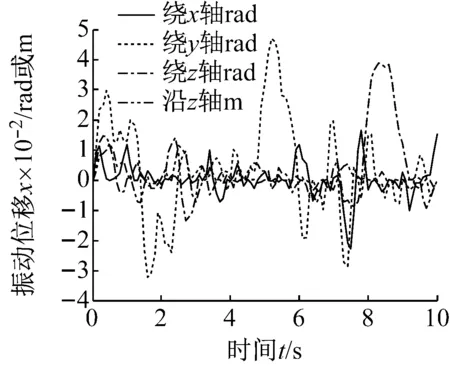
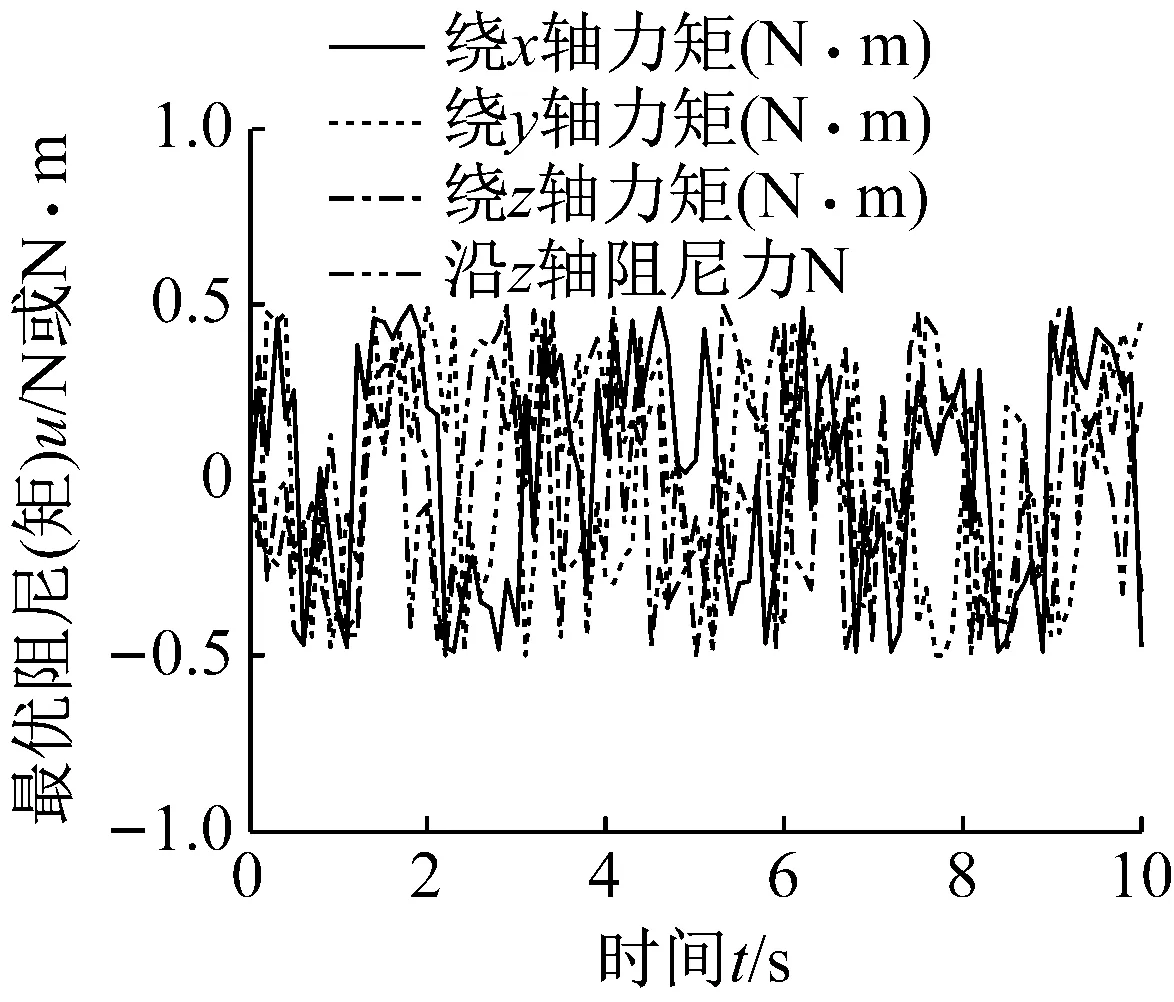
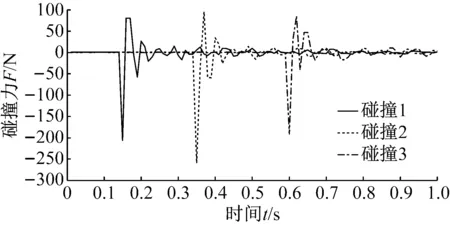
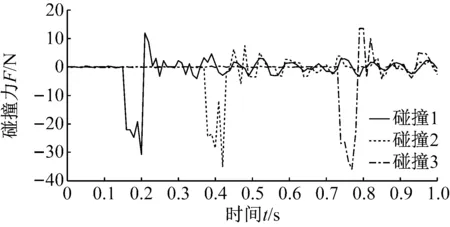
(2) 中间段(1 (14) 式中:Fkz=-F(k-1)y,Mkz=-M(k-1)y。 (3) 末端(k=N+1) (15) 式中:F为末端瞬时冲击力;M为末端瞬时冲击力矩。 对于包含(N+1)个刚体段的串联型机构,其Kane动力学方程 (16) 式中:l=1, 2, 3, …, 6N+6。 将偏角速度,偏线速度,等效主动力(矩),等效惯性力(矩)代入式(16),并与运动学方程式(4)联立,得到多级阻尼柔性抓捕机构的(6N+6)维非线性微分方程组 (17) 微粒群算法根据生物群觅食的思想,利用个体局部信息和群体全局信息指导搜索,通过不断迭代优化自变量使得目标函数实现最优,对于大型复杂问题的优化有良好的适用性[13]。空间捕获过程中,基座和柔性抓捕机构均可能因碰撞冲量引起失稳,此时,可通过优化控制多个阻尼器输出的阻尼力来实现漂浮基与柔性抓捕机构整体系统的镇定控制。 捕获时的碰撞冲量会引发柔性抓捕机构的振动,进而在各个关节处产生弹性变形力(矩),且漂浮基座的位置和姿态会受到与其相连的关节处弹性变形力(矩)的影响,因此,完成捕获后,漂浮基座与抓捕机构变成不稳定动力系统,而镇定控制的目标即抑制该系统各个关节处的弹性变形量。目标函数可表示为 (18) 式中:n=6N,x1,x2,…,xn为抓捕机构各关节处沿6个方向的振动变形量,max(xn)为抓捕机构各关节处沿6个方向预先设定的最大允许振动变形量,可根据初始碰撞冲量及操作任务指标确定,当各关节处振动变形小于对应的最大允许振动位移时,即认为达到控制要求。a1,a2,…,an是加权系数,且满足a1+a2+…+an=1。 由于传统的微粒群算法容易陷入局部最小,故采用线性递减、带有惯性权重的微粒群进化算法进行优化计算,如式(19)所示,以便初始时刻快速搜索,快接近最优位置时,减慢搜索速度,加强局部搜索能力。 vij(t+1)=h·vij(t)+c1·rand1·[pij(t)-zij(t)]+ c2·rand2·[pgj(t)-zij(t)] zij(t+1)=vij(t+1)+zij(t) h=h2-c·(h2-h1) (19) 式中:vij(t)为微粒的飞行速度;zij(t)为微粒的当前位置;pij(t)为个体全局最好位置;pgj(t)为群体全局最好位置;c1为认知学习系数;c2为社会学习系数;c为系数;h∈[h1,h2]为惯性权重;正定常数rand1,rand2∈[0,1]为随机数。 对于目标函数(18),当抓捕机构各关节处每个自由度方向的振动位移xi(i≤6N) 小于对应的最大允许振动变形量max(xi),即f(t)<1,说明镇定控制已达到期望的要求,此时可终止微粒群迭代算法,并输出该时刻求得的阻尼力,即为最优阻尼力。 具体的控制算法流程为 步骤1 根据初始时刻的碰撞动量和抓捕机构的 初始构型,由运动学方程(4)和动力学方程(17)计算t时刻抓捕机构的广义坐标xl(t); 步骤2 由xl(t)和微粒群算法(19),通过以下迭代步骤(i)、(ii)和(iii)求解可得到t时刻可控阻尼器的最优阻尼力: (i) 定义微粒群规模m,根据可控阻尼器的数量确定粒子维数d,每个可控阻尼器的阻尼力大小对应微粒群中粒子的位置。初始化微粒群中每一个粒子的位置zij,将xl(t)和zij代入式(4)和(17),计算每个粒子(t+1)时刻的广义坐标xl(t+1),并代入式(18)计算适应值Fg1,并将当前位置作为pij和pgj(t)。 (ii) 根据式(19)更新粒子的当前位置,并将xl(t)和代入式(4)、(17)、(18)继续计算Fg2,比较Fg2和Fg1的大小,将适应值更小的粒子位置作为pij和pgj(t),并得到对应的Fg。 (iii) 判断当前适应值Fg是否小于1。若不满足要求,则重复步骤(ii)。若满足要求,说明满足算法终止条件,输出当前的全局最好位置pgj(t),作为可控阻尼器t时刻的阻尼力u(t)。 步骤3 将u(t)和xl(t)代入式(4)和(17),计算(t+1)时刻抓捕机构的广义坐标xl(t+1)。重复利用步骤2计算(t+1)时刻的最优阻尼力u(t+1),循环至终。 微粒群多级阻尼优化镇定控制的流程框图如图2所示。 为验证所提出方法的有效性,对某型3关节12自由度的抓捕机构进行多级阻尼镇定控制仿真。由图1可知,抓捕机构各个关节处沿Oixi、Oiyi直线方向的碰撞动量可通过多自由度机构的传递与转换,由三个旋转阻尼器间接镇定,故只需保留Oizi轴的直线阻尼器。因此,该机构每个关节可设计4个自由度,分别是绕Oixi、Oiyi、Oizi轴的转动自由度以及沿Oizi轴的直线运动自由度。在各个自由度方向上可安装对应的直线或旋转阻尼器,3关节抓捕机构共包含12个阻尼器。 图2 微粒群多级阻尼优化镇定控制流程图 系统仿真参数:末端瞬时冲击力F=(100,100,100)N,瞬时冲击力矩M=(100,100,100) N·m。基座质量200 kg,惯性张量I1=diag (53.3,53.3,66.7)kg·m2。抓捕机构各连杆的质量mk=8 kg,惯性张量Ik=diag(2.5,2.5,5)kg·m2。旋转式阻尼器的弹性系数K旋转=40 N/m,阻尼力矩输出范围:Mu∈[-0.5,0.5]N·m,直线式阻尼器的弹性系数K直线=40 N/m,阻尼力输出范围:Fu∈[-0.5,0.5]N。微粒群规模:10,粒子维数:12,认知学习系数:c1∈[0.5,2.5]线性递减,社会学习系数:c2∈[0.5,2.5]线性递增,惯性系数:h∈[0.5,2.5]线性递减,最大迭代次数:nmax=50。 分别对未施加控制和微粒群多级阻尼优化控制下的空间抓捕动力学进行仿真,对比施加控制前后抓捕机构和基座的动力学响应差异。图3、图5和图7分别对应了柔性抓捕机构第1、第2和第3关节在未施加控制时的振动位移响应,图4、图6和图8分别对应了柔性抓捕机构第1、第2和第3关节在施加多级阻尼镇定控制后的振动位移响应。以第1关节的动力学响应为例进行对比分析可见,在末端碰撞力(矩)的作用下,未施加控制时第1关节的最大扭转振动位移可达0.08 rad,最大直线振动位移可达0.06 m,而多级阻尼镇定控制可以保证第1关节的最大扭转振动位移减小至0.01 rad以内,最大直线振动位移减小至0.015 m以内。图9给出了第1关节处四个阻尼器对应的最优阻尼力,均连续有界,表明利用本文控制方法求得的阻尼力是完全可控的。与第1关节的动力学响应规律类似,第2和第3关节处的振动位移均在多级阻尼控制的镇定作用下实现了大幅度的收敛,实现了振动抑制。同理,图10和图11表明第2和第3关节处的四个阻尼器也能输出连续有界的可控阻尼力。 图12和图13分别给出了受控前后基座在惯性坐标系下的质心位移和姿态角速度对比,可见,在多级阻尼的镇定控制作用下,基座沿y轴方向的质心位移从未控时的最大值0.18 m减少至0.02 m,基座绕y轴的姿态角速度从未控时的最大值0.032 rad/s减少至0.007 rad/s,有效地规避了漂浮基座的姿态倾斜和角动量超限。 由上述仿真结果可知,采用多关节多自由度柔性抓捕机构完成空间捕获任务,可大幅度减小碰撞冲量对基座的扰动,因而能保证基座的稳定性。同时,基于微粒群优化算法的多级阻尼镇定控制策略能实现柔性抓捕机构在多维空间内的振动抑制。 图3 无镇定控制时第1关节的振动位移 Fig.3 Vibration displacements of 1st joints without stabilization control 图4 多级阻尼镇定控制时第1关节的振动位移 Fig.4 Vibration displacements of 1st joints with multistage damping stabilization control 图5 无镇定控制时第2关节的振动位移 Fig.5 Vibration displacements of 2nd joints without stabilization control 图6 多级阻尼镇定控制时第2关节的振动位移 Fig.6 Vibration displacements of 2nd joints with multistage damping stabilization control 图7 无镇定控制时第3关节的振动位移 Fig.7 Vibration displacements of 3rd joints without stabilization control 图8 多级阻尼镇定控制时第3关节的振动位移 Fig.8 Vibration displacements of 3rd joints with multistage damping stabilization control 图9 多级阻尼镇定控制时第1关节的阻尼力(矩) Fig.9 Damping forces (moments) of 1st joint in multi stage damping stabilization control 图10 多级阻尼镇定控制时第2关节的阻尼力(矩) Fig.10 Damping forces (moments) of 2nd joint in multi stage damping stabilization control 图11 多级阻尼镇定控制时第3关节的阻尼力(矩) Fig.11 Damping forces (moments) of 3rd joint in multi stage damping stabilization control 图12 受控前后基座质心的位移 图13 受控前后基座的角速度 选用SG-MRF2035型磁流变液,分别研制了直线式和旋转式磁流变阻尼器,实物如图14(a)和14 (b)所示,采用YH1718双路稳压稳流跟踪电源对磁流变阻尼器进行“电流-阻尼力(矩)”伺服控制,经过测试实验得知,直线式磁流变阻尼器的有效阻尼力输出范围为[-7.5,7.5]N, 旋转式磁流变阻尼器的有效阻尼力矩输出范围为[-0.05,0.05]N·m。按照文献[12]的结构设计方案研制了具有二关节四级阻尼的柔性抓捕机构原理样机,实物如图14(c)所示。将该柔性抓捕机构整体放置于水平气浮平台上,气泵压力设置为1.5 MPa,靠气浮足喷出的高压气体反力来抵消机构自身的重力,此时可研究具有多级阻尼的柔性抓捕机构受到碰撞冲击力后在水平面内的镇定控制效果。 (a)直线式磁流变阻尼器(b)旋转式磁流变阻尼器 (c) 柔性抓捕机构 Fig.14 Ground principle prototype of flexible capturing mechanism with two joint and four stage damping 实验方案:柔性抓捕机构处于完全伸展状态的直线位型,在其末端设计一个单摆装置,利用重物块下落至最低处时对柔性抓捕机构末端产生的冲击力来模拟抓捕过程的碰撞力。在基座与柔性抓捕机构的连接法兰处安装ATI-Nano17型六维力传感器,通过对该处耦合力的在线测量来验证具有多级阻尼的柔性抓捕机构对基座扰动力的镇定控制效果。在直线式磁流变阻尼器的运动轴端安装RH100X30D05A型光栅尺用来测量该轴方向的直线振动位移,在旋转式磁流变阻尼器的运动轴端安装EAC58P轴套型绝对值编码器用来测量该轴方向的旋转振动位移。 若单摆装置的重物块质量为m,固定摆长为l,则当重物块以初始角度θ落下时,重物块在最低点获得的动量为 设碰撞后单摆弹回的角度为β,则碰撞后重物块的动量为 此时,可计算抓捕机构末端受到的碰撞力为 式中:Δt为碰撞时间,可通过力传感器获得。 重物块质量m=2.0 kg,固定摆长l=203 mm,以θ=30°作为初始角度释放单摆重物,通过测量磁流变阻尼器分别在断电和伺服状态下六维力传感器的碰撞力数值,开展无多级阻尼和有多级阻尼状态下的镇定控制对比实验,连续进行碰撞实验各三次,实验结果如图15所示。由图15(a)可以看出,磁流变阻尼器在断电状态下,抓捕机构末端的碰撞力对基座的扰动力平均值约为200 N,最大值约为261 N。由图15(b)可以看出,磁流变阻尼器在伺服状态下,抓捕机构末端碰撞力对基座的扰动力平均值约为35 N,最大值约为37.5 N。图15(c)表明在抓捕机构的当前位型和碰撞力作用下,第1关节和第2关节内的旋转式磁流变阻尼器均无输出,由直线式磁流变阻尼器起主导作用,且其输出阻尼力连续有界,相应地,图15(d)给出了第1关节和第2关节内直线式磁流变阻尼器对应轴的振动位移,取三次实验的平均值,可见,在多级阻尼器作用下,各关节对应轴的振动位移渐进收敛。 (a) 磁流变阻尼器断电状态下基座受到的扰动力 (b) 磁流变阻尼器伺服状态下基座受到的扰动力 (c) 直线式磁流变阻尼器伺服状态下输出的阻尼力 (d) 磁流变阻尼器伺服状态下两关节的直线振动位移 Fig.15 Collision simulation test results of two-joint four-stage damping flexible capturing mechanism 该实验结果表明具有多级阻尼的柔性抓捕机构可大幅度减小碰撞冲量对基座的扰动,对规避漂浮基座的姿态倾斜和角动量超限可起到积极作用。同时,柔性抓捕机构各个关节的振动位移在多级阻尼的作用下均渐进收敛,能保证系统的整体镇定。 (1) 提出了一种具有多级可控阻尼的串联型柔性抓捕机构广义模型,用以实现空间捕获任务的柔顺化。 (2) 通过在柔性抓捕机构的关节处设计多维可控阻尼器,可以实现对空间任意方向碰撞冲量的缓冲和卸载。 (3) 采用微粒群优化算法可以实现多级阻尼的优化配置,保证基座稳定的同时实现柔性机构的振动抑制,最终完成系统的镇定控制。 [1] XU W L, YUE S G. Pre-posed configuration of flexible redundant robot manipulators for impact vibration alleviating[J]. IEEE Transactions on Industrial Electronics, 2004, 51(1): 195-200. [2] 丛佩超, 孙兆伟. 空间机械臂捕捉空间目标分析[J]. 上海航天, 2009(4):7-11. CONG Peichao, SUN Zhaowei. The research of free-floating space manipulator capture object[J]. Aerospace Shanghai, 2009(4): 7-11. [3] WEI Cheng, LIU Tianxi, ZHAO Yang. Grasping strategy in space robot capturing floating target[J]. Chinese Journal of Aeronautics, 2010, 23(5): 591-598. [4] LIU Shengping, WU Licheng, LU Zhen. Impact dynamics and control of a flexible dual-arm space robot capturing an object[J]. Applied Mathematics and Computation, 2007, 185(2): 1149-1159. [5] DONG Qiuhuang, CHEN Li. Impact dynamics analysis of free-floating space manipulator capturing satellite on orbit and robust adaptive compound control algorithm design for suppressing motion[J]. Applied Mathematics and Mechanics, 2014, 35(4): 413-422. [6] 董楸煌, 陈力. 柔性空间机械臂捕获卫星碰撞动力学分析、镇定运动神经网络控制及抑振[J]. 机械工程学报, 2014, 50(9): 34-42. DONG Qiuhuang, CHEN Li. The impact dynamics analysis of flexible space manipulator capturing a satellite and neural network calming motion control and vibration suppression[J]. Journal of Mechanical Engineering, 2014, 50(9): 34-42. [7] CHU Ming, CHEN Gang, JIA Qingxuan, et al. Simultaneous positioning and non-minimum phase vibration suppression of slewing flexible-link manipulator using only joint actuator[J]. Journal of Vibration and Control,2014,20(10): 1488-1497. [8] BIAN Yushu, GAO Zhihui. Impact vibration attenuation for a flexible robotic manipulator through transfer and dissipation of energy[J]. Shock and Vibration, 2013, 20(4): 665-680. [9] CHU Ming, ZHANG Yanheng, CHEN Gang, et al. Effects of joint controller on analytical modal analysis of rotational flexible manipulator[J]. Chinese Journal of Mechanical Engineering, 2015, 28(3): 460-469. [10] BALAMURUGAN L, JANCIRANI J, ELTANTAWIE M A. Generalized magnetorheological (MR) damper model and its application in semi-active control of vehicle suspension system[J]. International Journal of Automotive Technology, 2014, 15(3): 419-427. [11] NGUYEN H, THAI C, SHARF I. Capture of spinning target with space manipulator using magneto rheological damper[C]//AIAA Guidance, Navigation, and Control Conference. Toronto, Canada:American Institute of Aeronautics and Astronautics Inc., 2010. [12] 褚明, 董正宏, 孟庆川, 等. 基于十字轴结构的软接触关节: ZL201410784247.7[P]. 2014-12-16. [13] 郭迎庆, 徐赵东, 费树岷, 等. 磁流变智能结构的微粒群优化控制[J]. 振动与冲击, 2011,30(9): 59-63. GUO Yingqing, XU Zhaodong, FEI Shumin, et al. PSO control used in magnetorheologicaI intelligent structures[J]. Journal of Vibration and Shock, 2011,30(9): 59-63.
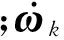
2.4 动力学方程


3 基于微粒群的多级阻尼优化控制
3.1 微粒群算法的适应度函数
3.2 多级阻尼优化的镇定控制
4 数值仿真








5 实验验证




6 结 论
