利用一元二次方程解三角形案例分析

◎甘述鸿 张爱存

(甘肃省武威市天祝藏族自治县第二中学，甘肃 武威 733299)

初中数学教学中，以三角形的边长、锐角三角函数作为一元二次方程的根或者系数的问题，融会了几何知识和代数知识，是一种综合性较强的题型.由于这类题目侧重于考查学生分析问题和解决问题的综合能力，所以在历届中考考试中屡见不鲜.本文举例说明解决此类问题的常用方法.

一、利用根的判别式求解

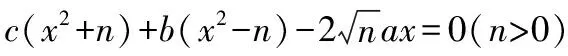
∴na2-n(c2-b2)=0，即a2+b2=c2，

∴△ABC是直角三角形.

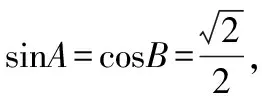
二、利用韦达定理求解

例3(连云港市中考题)设△ABC的三边分别是a，b，c，其中a，b是方程x2-(c+2)x+2(c+1)=0的两个实数根，试判断△ABC是否为直角三角形，并说明理由.

解由韦达定理，得a+b=c+2，ab=2(c+1)，

∴a2+b2=(a+b)2-2ab=(c+2)2-4(c+1)=c2，

∴由勾股定理的逆定理可知△ABC是直角三角形.

例4(昆明市中考题)在△ABC中，∠C=90°，斜边AB=10，直角边AC，BC的长是关于x的方程x2-mx+3m+6=0的两个实数根.

(1)求m的值；

(2)计算sinA+sinB+sinA·sinB.

解(1)根据韦达定理，得

AC+BC=m，AC·BC=3m+6.

在Rt△ABC中，AC2+BC2=100，

即(AC+BC)2-2AC·BC=0，

代入整理得m2-6m-112=0.

解得m1=14，m2=-8(舍去).

(2)AC+BC=m=14，AC·BC=3m+6=3×14+6=48，

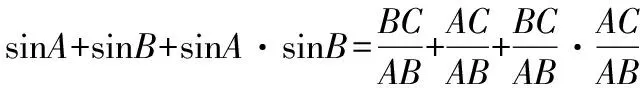
三、构造一元二次方程，利用解方程求解

例5(河北省中考题)已知：k>1，b=2k，a+c=2k2，ac=k4-1，则以a，b，c为边的三角形( ).

A.一定是等边三角形 B.一定是等腰三角形

C.一定是直角三角形 D.形状无法确定

解由于a+c=2k2，ac=k4-1，

所以a，c是方程x2-(2k2)x+k4-1=0的两根.

解得a=k2-1，c=k2+1.

∴a2+b2=(k2-1)2+(2k)2=k4+2k2+1=(k2+1)2=c2，

∴以a，b，c为边的三角形是直角三角形，应选C.

四、综合利用根的判别式、韦达定理、根的意义等知识求解

(1)略；

(2)若等腰△ABC的一边长a=4，另两边的长b，c恰好是这个方程的两个根，求△ABC的周长.

解(2)∵△ABC是等腰三角形，

∴有两边长相等.

若b=c，由于b，c都是已知方程的根，

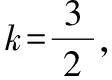
∵a=4，这时b+c=a，不合题意，

∴这种情况不可能.

若b，c中有一条与a相等，不妨设b=a=4.

∵b是所给方程的根，

∴b+c=2k+1=6，从而c=2.

∵a+b=8>c，符合题意，

∴△ABC的周长为10.