待定系数法与配方法的结合

◎张冬梅

(云南师范大学数学学院，云南 昆明 650500)

一、前 言

待定系数法是数学中的重要方法，是在知道问题答案形式的前提下，根据求解问题的特征，通过引入一些待定的系数，将要解决的数学问题转化成一个含有待定系数的恒等式，然后利用恒等式的性质求出待定的系数，使问题得到解决[1].

配方法是对数学式子进行一种定向变形(配成“完全平方”)的技巧，通过配方找到已知与未知的联系，达到化繁为简，化难为易.在中学数学中，配方法主要适用于：含有二次方程、二次不等式、二次函数、二次代数式的讨论与求解，或者是缺中间交叉项xy的二次曲线等问题.配方法使用的最基本的配方依据是完全平方公式(a±b)2=a2±2ab+b2，将这个公式灵活运用，可以得到一些基本的配方形式，如：

a2+b2=(a+b)2-2ab=(a-b)2+2ab，

a2+ab+b2=(a+b)2-ab=(a-b)2+3ab

a2+b2+c2=(a+b+c)2-2(ab+bc+ac)

1+sin2α=1+2sinαcosα=(sinα+cosα)2.

很多数学问题，若巧用配方法，会将数学问题化繁为简，化难为易，对利用实数平方的非负性来解决有关问题也有很大的作用[2].只要用心体验、感悟，就能明白配方法的妙用.下面介绍利用待定系数法将多项式进行配方的通式，希望对某些数学问题解决有所帮助，也希望对想出此类题目的数学教学工作者有点帮助.

二、利用待定系数法将代数式化为完全平方式

(一)一元偶次幂形式

常见的一元偶次幂形式的式子ax2+bx+c，将之进行配方可以帮助我们解决与二次函数、一元二次方程、求代数式的值等有关的问题.这类式子进行配方难度不大，对学生来说印象最深刻的就是教师在黑板上推导一元二次方程的求根公式的时候，那是学生首次接触配方法.

①ax2+bx+c

解：假设ax2+bx+c=a(x+k)2+h=ax2+2akx+ak2+h.

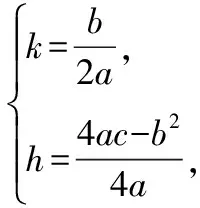
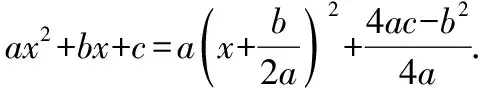
② 对关于x的方程ax4+bx3+cx2+dx+e=0(a≠0)的配方，只需将等号左右两边同时除以x2就可以转化成熟悉的二次形式进行配方，过程如下：

或者先不考虑把常数项计算出来，有

代数问题中常出现求代数式最大值或者最小值的情况，在解题时学生需想尽办法将各种式子向配方法的表现形式靠拢，达到简化式子的目的，让题目变得简单，而待定系数法便是一种行之有效的方法，使学生在解题时更加得心应手.

例1求二次函数y=2x2+4x+5的对称轴方程和最小值.

解利用待定系数法配方得y=2(x+1)2+3，

∴对称轴方程是x=-1，由于2>0，所以函数的最小值为3.

例2已知a，b∈R，关于x的方程x4+ax3+2x2+bx+1=0有一个实根，求a2+b2的最小值.

从而a2+b2≥8.

因此，a2+b2的最小值为8.

(二)二元形式

对于二元形式的式子的配方，此处以二元函数为例进行，相应的方程形式的配方就不再赘述.关于x，y的函数f(x，y)=ax2+by2+cxy+dx+ey+g.

① 若有|a|<|b|且有c=2a，则有

假设f(x，y)=a(x+y+k)2+(b-a)(y+h)2+g-ak2-(b-a)h2=ax2+by2+2axy+2akx+[2ak+2h(b-a)]y+g.

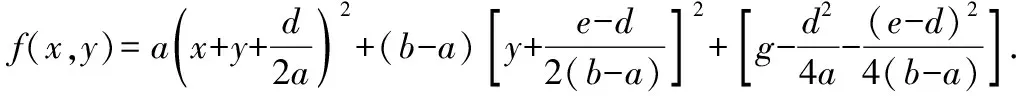
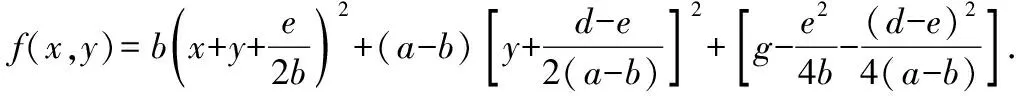
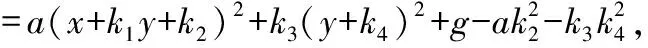
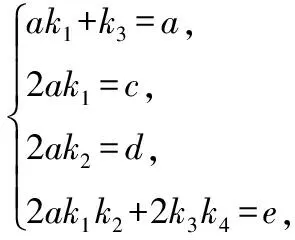
④ 若有a=b且有|d|>|e|，则同③利用待定系数法有

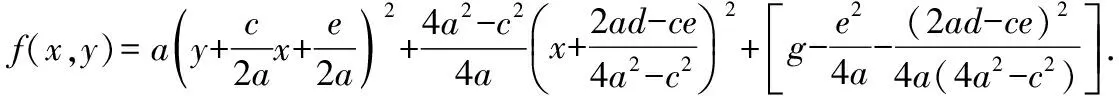
上述几种形式的代数式的配方过程不仅可以使学生在做某些代数问题时有法可循，也可以帮助教师或相关人士在命制试题时配凑相关数据，求解相应的问题.

例3求实数x，y的值，使得f(x，y)=(y-1)2+(x+y-3)2+(2x+y+6)2达到最小值.

解f(x，y)=(y-1)2+(x+y-3)2+(2x+y+6)2=5x2+3y2+6xy-30x-20y+46.

设f(x，y)=3(x+y+a)2+2(x+b)2+c=5x2+3y2+6xy+(6a+4b)x+6ay+3a2+2b2+c.

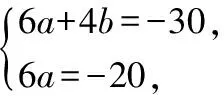
三、结 语

综上所述，利用“配方法”来求解一类条件式、函数式的一元二次式、一元四次式、二元二次式甚至一些三元式的问题，往往十分简洁流畅，给人以数学美的享受.

我国著名的数学家华罗庚在谈到学习待定系数法的体会时曾说过：“难处不在于有了公式去证明，而在于没有公式之前，怎样去找出公式来”.待定系数法和配方法都是解决数学问题的有力工具，而将两者结合起来应用有时会让我们在解决问题的时候事半功倍.本文主要介绍的是如何将函数式或者方程式通过待定系数法整理成完全平方的形式，从而解决数学问题.当然，待定系数法的应用远远不止这些，关于它的应用还有待我们继续研究.

[1]张保霞.浅析待定系数法在解题中的应用[J].科技展望，2017(6)：216.

[2]刘志国.初中数学方法及其应用[M].重庆：重庆出版社，1991.