浅谈在高三复习中如何利用分段函数教学提高学生的抽象思维能力

◎曹颖慧

(保定市第二中学，河北 保定 071000)

一、着力于教材

抽象思维能力的培养不是凭空生成的，它源于教材，为抽象思维能力的培养提供了基础[1].人民教育出版社A版《普通高中课程标准实验教科书·数学·必修1》中有10多个例题和习题，虽然学生在高一的时候已经学习了分段函数，但是知识是循环式上升的，抽象思维能力也是逐步提升的，高三再复习这些知识，会对函数有更深刻的理解.将这10多个习题按照难易程度排队，由浅入深的复习.

A级：问题简单、直观、明了，学生容易解答.

B级：给出了具体的分段函数，按照要求做出图像就行.

C级：需要学生先写出分段函数，再解决后面的问题.

D级：利用分段函数解决实际问题.

通过复习，学生在知识上，对函数的对应法则、定义域、值域、图像、集合知识的运用等要有更深刻的理解；在思想方法上，有分类讨论、数形结合等；提高基本初等函数图像、性质、解析式等的理解掌握程度[2].

二、以高考题为源深化拓展

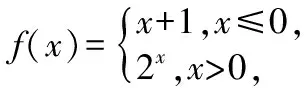
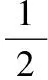
高考命题原则是在知识交汇处设置考题，有时分段函数不仅仅是出现在函数方面.

例2(2012年新课标全国卷第18题)某花店每天以5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售.如果当天卖不完，剩下的玫瑰花做垃圾处理.

(Ⅰ)若花店一天购进17枝(文科)(理科16枝)玫瑰花，求当天的利润y(单位：元)关于当天需求量n(单位：枝，n∈N*)的函数解析式；

(Ⅱ)略.

例3(2016年全国卷Ⅰ文科第19题)某公司计划购买1台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：(图略)

记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用(单位：元)，n表示购机的同时购买的易损零件数.

(Ⅰ)若n=19，求y与x的函数解析式；

(Ⅱ)略；

(Ⅲ)略.

例4(2016年全国卷Ⅱ文科第17题)等差数列{an}中，a1+a4=4，a5+a7=6.

(Ⅰ)求{an}的通项公式；

(Ⅱ)设bn=[an]，求数列{bn}的前10项和，其中[x]表示不超过x的最大整数，如[0.9]=0，[2.6]=2.

例5(2016年全国卷Ⅱ理科第17题)Sn为等差数列{an}的前n项和，且a1=1，S7=28.记bn=[lgan]，其中[x]表示不超过x的最大整数，如，[0.9]=0，[lg99]=1.

(Ⅰ)求b1，b11，b101；

(Ⅱ)求数列{bn}的前1 000项和.

这是姊妹题，以理科为例分析：(Ⅰ)由等差数列的知识得到an=n，那么bn=[lgn]，得到b1=[lg1]=[0]=0，b11=[lg11]=1，b101=[lg101]=2.

在科学研究中，科学抽象的具体过程是千差万别的，没有千篇一律的模式.通过分段函数的复习要教会学生抽象的过程：第一步：分离，就是暂时不考虑我们所要研究的对象与其他各个对象之间各式各样的联系，从学科的研究领域出发，从探索某一种规律性出发，确定自己所特有的研究对象；第二步：提纯，就是在思想中排除那些模糊基本过程、掩盖普遍规律的干扰因素，从而使我们能在纯粹的状态下对研究对象的性质及其规律进行考察；第三步：简略，就是对纯态研究的结果进行的一种处理，或者说是对研究结果的一种表述方式，在科学研究过程中，对复杂问题做纯态的考察是一种简化，另外，对于考察结果的表达也有一个简略的问题.这个过程概括为：分离—提纯—简略.

抽象思维能力的培养不是一蹴而就、一朝一夕的，需要由浅入深，由表及里，多次渗透，反复训练[2].

[1]楼肇庆.高三数学教学落实核心素养的若干着力点[J].中学数学教学参考，2017(16):36-39.

[2]郑云初.点击分段函数[J].中学数学教学参考，2004(7):6-8.