数列求和的方法探讨

◎陈 继

(曲靖工商职业技术学校，云南 曲靖 655000)

数列属于高中数学非常重要的组成部分，其在培养学生思维能力和逻辑推理能力，有着不可替代的作用.同时，在历年的数学高考中，数列求和是常考的题型.数列求和试题不仅仅是考查数列综合知识点，同时也考查学生的知识融会贯通能力和综合分析能力，对于学生数学素养要求非常高.因此，在实践教学过程中，教师必须对数列求和问题引起重视，引导学生掌握各种求和方法，能做到熟练灵活地运用.

一、拆项法

在面对有些数列求和的问题时，如果题目中的数列可以进行拆分，如拆成等差数列或者是等比数列的和，则可以采取拆项法进行求解，只需利用等比或等差数列的求和公式，将原数列中的n次方项当成一个整体.

二、裂项相消法

把数列的通项拆成两项之差，即把数列的每一项都按同一种方法拆成两项的差，使得求和时，一些正项和负项组能互相“抵消”为零.这是分解与组合思想在数列求和中的具体应用，裂项法的实质，就是将数列中的每项(通项)分解，然后重新组合，使之能消去一些项，最终达到求和的目的.

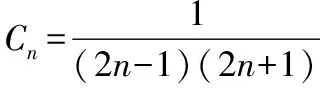
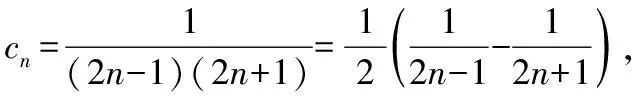
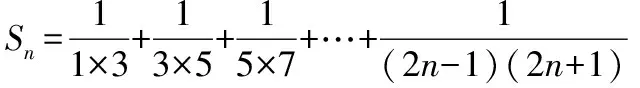
三、分组转化法

把数列的每一项分解成两(多)项，或者把数列的项重新组合，使其转化成两(多)个等比数列或者等差数列的和，即对通项进行分解或组合，将原数列转化成若干个容易求和的数列.

四、错位相减法

错位相减法，主要是用于有一个等差数列和一个等比数列对应项之积所构成的数列求和问题中.错位相减法的解题方法非常重要，在最近几年的高考试题中，均出现了此方面内容.因此，学生必须对此种解题方法做到心中有数，熟练运用.在进行等比数列的前n项和的公式推导中，也常会运用此种方法.

比如，在如下例题中：Sn=1+3x+5x2+7x3+…+(2n-1)xn-1.

①

解答由题可知，{(2n-1)xn-1}的通项是等差数列{2n-1}的通项与等比数列{xn-1}的通项之积，设xSn=x+3x2+5x3+7x4+…+(2n-1)xn.

②

通过将①-②相减可以得出(1-x)Sn=1+2x+2x2+2x3+2x4+…+2xn-1-(2n-1)xn.

再利用等比数列的求和公式，可以得出：

由此可以得出，

五、合并法求和

针对一些特殊的数列，将某些项合并在一起就具有某种特殊的性质，因此，在求数列的和时，可将这些项放在一起先求和，然后再求Sn.

比如，如下例题，在各项均为正数的等比数列中，若a5a6=9，求log3a1+log3a2+…+log3a10的值.

解设Sn=log3a1+log3a2+…+log3a10.

Sn=(log3a1+log3a10)+(log3a2+log3a9)+…+(log3a5+log3a6)

=(log3a1·a10)+(log3a2·a9)+…+(log3a5·a6)

=log39+log39+…+log39=10.

六、奇偶数讨论方法

有的数列求和，不仅需要考虑分段，同时还应当注意到奇数和偶数时的情况；然后再将所有的情况综合起来的最终结果.遇到此种类型的题目，务必加以细心考虑.如果题目与奇数有关，通常情况下幂为n-1或者是n+1，这是当n为偶数时，幂就是奇数；当n为奇数时，幂就是偶数.

七、猜想法

一些数列求和问题，需要学生结合所掌握的知识和数学思想，大胆猜想和假设.尤其是遇到难度较大的数列求和问题时，更需要认真审题，仔细推敲，思考其内在的规律.首先，需要将S1，S2，S3，S4，S5等明确地计算出来，发现其中的规律；然后再利用归纳法进行证明.对于数列前n项和的计算方法有很多，比如，递推法、常数列法以及综合法，等等.

八、总 结

总而言之，在高中数学教学中，数列求和属于数列教学重要的组成部分，数列求和对学生的数学综合能力要求较高，尤其是逻辑推理能力、归纳猜想能力以及运算转化能力，等等.在具体的数列求和解题过程中，教师应当引导学生对各种方法做到灵活运用，从而不断提高解题正确率.

[1]吕茂林.数列求和方法探讨[J].读与写：教育教学刊，2013(6)：112.

[2]吴琪.浅谈数列求和的类型及解题方法分析[J].数学学习与研究，2014(11)：100-101.

[3]黄雪.数列求和的常用方法与技巧[J].西部素质教育，2016(4)：183.

[4]黎东辉.高考试题中几种常见的数列求和方法[J].赤子(上中旬)，2015(17)：279-280.