避典型错误,方能更易取胜
——以解三角形中错误资源的利用为例
2018-03-23◎程莹
◎程 莹
(浙江省丽水市庆元县庆元中学,浙江 丽水 323800)
解三角形是高中数学中很基础却又很重要的知识,主要考查正弦定理和余弦定理的正确使用,属于历年考试必考的题目,但从考试结果来看,这部分得分不理想.根据“错误”是一种可再生教学资源的教学理念,首先,教师正视学生的错误,引导学生发现错误,发现错误之时,就是开始降低出错率的最佳时机;其次,要引导学生主动去纠正错误,找出错误的根源;再次,培养学生及时反思,对错误分类整理,落实纠错并进行针对练习的好习惯.笔者在解三角形知识点的复习教学中,搜集整理了学生在下述三方面的典型错误,引导学生经历发现错误——纠正错误——评析错误——发展思维的过程,学生方面反馈效果很好.
一、三角函数的知识不扎实
例1(2016·浙江卷理)在△ABC中,角A,B,C对的边记为a,b,c,已知b+c=2acosB.
(1)证明:A=2B;
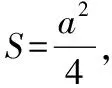
错解(1)由正弦定理得sinB+sinC=2sinAcosB,
故sinB+sin(A+B)=sinB+sinAcosB+cosAsinB,
移项运算,得sinB=sin(A-B),
所以B=A-B,得证A=2B.
师:上述解法中错误不止一处,试一试,你能找出几处?
生:在(1)中,由sinB=sin(A-B),角A,B∈(0,π),故0 评析本题很值得作为典例,是学生经常出错的类型.根源在于由三角函数值相等不能准确判断两角之间的关系.解三角形需要三角函数作为基础知识,需要多练习. 例2在锐角△ABC中,角A、B、C的对边分别为a,b,c,b·cosC=(2a-c)·cosB. (Ⅱ)已知边b=1,求a+c的范围. 评析解法1中,首先未考虑到基本不等式的缺点,即只能计算最大值或者最小值,那么该解法如何修正能得到正确范围呢? 评析解法2中,使用函数思想解题是该解法的优点,但是角A的范围错误,如何修正该解法,从而得到正确结果呢?(学生分组讨论、交流) 生:锐角三角形应该保证每一个角为锐角. 小结上述两种解法,经过纠错环节,都成为正确的解法,但是方法2的函数思想更优越,符合求范围题型的内在要求.若本题仅要求解最大值,或者三角形未限定为锐角三角形,则可以采用基本不等式.此外,本道题中锐角三角形是关键信息,审题时要重点标记. 例3在△ABC中,内角A,B,C的对边分别为a,b,c. 评析本道题有2个小问,虽然结果都是正确的,但是思维有很大漏洞. 对于(1)在三角形中,sinA≠0是肯定的,所以可以认为正确. 但在(2)中,cosA=0是可以出现的,故需要分类讨论. 评析本题是反定式思维的一个典例,主要考查sinA和cosA在化简中的不同作用.从做过很多题目来看,95%情况是约掉一个角的正弦值,于是,学生形成定式思维,对cosA≠0也当作默认的,直接约掉导致出现隐形错误,这种失分很值得关注. 收集典型错误,建立错题集是解决学生反复犯同一种错误的最好方法.但对教师来说,也应该是一种好方法,有助于课堂的针对性,提高课堂效率,集中学生注意力,让学生经历从错误中走出来的亲身体验,对于后续降低解三角形这类题目的出错率有利无弊.
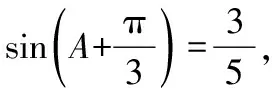
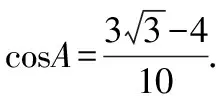
二、数学思想欠缺
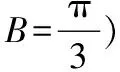
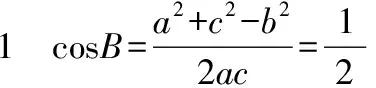
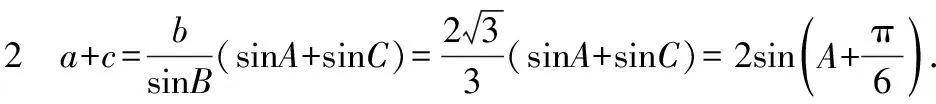
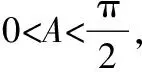
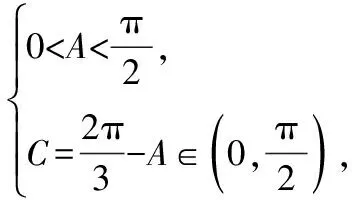
三、定式思维,运算不细心
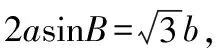

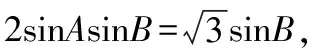
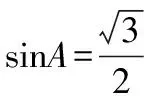
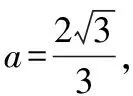
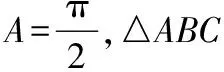
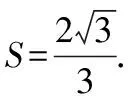
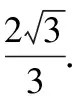
四、反 思
