群组决策论文名次的集对分析模型

田 园， 丁根宏

(河海大学 理学院，江苏 南京 211100)

高校在教育教学活动中常常会举行各种竞赛来丰富学生课外知识，提高学习技能，如数学建模比赛、英语竞赛、数学趣味比赛等。比赛结果根据评委老师打分进行排名，考虑到参与打分评委的主观差异性，参赛人水平的不确定性，打分结果的随机性，致使直接求和取均值的排名方法不能客观反映论文水平。在考生众多的论文型竞赛中，评委数量较少的限制通常将每篇论文随机分配给某几位评委进行评阅；设xij表示第j位评委对第i篇论文的评分，则评分矩阵x=(xij)是有残缺的，由于评分矩阵的不完整性和评委打分习惯不同使得最终排名结果与真实水平误差较大；为有效解决这些问题，国内外专家学者做了相关研究并提出不少解决方法，如T分数法[1]，填补残缺数据法[2,3]，加权T分数法[4,5]等；由于每位评委所评阅的论文不完全相同，论文水平本身的也有差异，T分数法缺乏对差异的考虑；而填补法多适用于残缺率小且数据之间有显著的相关性的情形，对于数据缺失率较高或数据之间没有显著的相关性性的情况，填补数据法就很难保证结果的准确。本文通过评委赋权法[6]进行第一轮评分排名，从中选出部分优秀论文进行二次评选，在第二轮评分排名中将评委打分时的确定因素与不确定因素作为一个系统加以处理，构建集对分析模型确定最终排名结果。通过模拟实验的数据显示该方法的科学性与准确性。

所谓群组决策[1-4]是指，设有s1,s2，…，sm共m个专家，他们构成决策群组G．被评估的对象(或称目标、指标)为B1,B2,…,Bn共n个．xij∈[I,J]是第i个专家对第j个被评对象的评分值．xij越大，si认为目标Bj越好．向量xi=(xi1,xi2,…,xin)T∈En和矩阵x=(xij)m×n(i=1,2,…,m,j=1,2,…,n)分别代表专家个体si和群组G在一次决策行为中所作的结论．为确保决策的科学性、民主性，人类的决策问题越来越依赖于群组，尤其是具有不确定性或依赖主观评价的问题．

1 论文的分配理论与模型分析

论文评阅的分配优化描述如下，设某次数学建模竞赛一共收到来自不同学校的m份论文，随机编号为1,2,…,m；此次阅卷的n位评委也来自这些学校，随机编号为1,2,…,n；并保证每份论文至少有s位评委评阅。

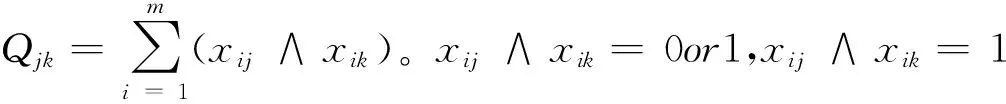
1.1 论文的最大交叉量的分析与描述

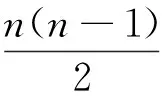
1.2 论文交叉分配的数学模型建立[7,8]

目标函数min{z=(maxQjk-minQjk)}

目标函数说明：使得任意两个评委所评阅论文的最大交叉量与最小交叉量之差的最大值最小，即保证评委所评阅的论文之间尽可能的交叉。

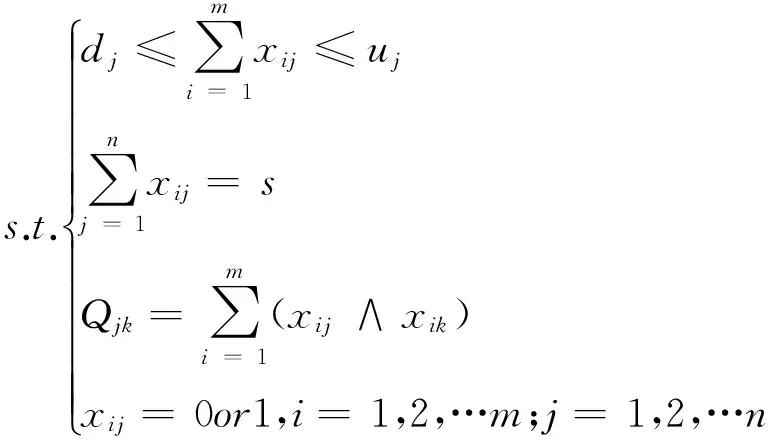
2 集对分析评价方法的理论基础

集对分析[9,10]是从系统的角度去认识确定性和不确定性的关系，并确定研究对象是一个确定不确定系统。是由赵克勤自1989年正式提出的新的不确定理论，被广泛应用于各行各业。

集对(Set Pair)，具有一定联系的两个集合组成的对子。

集对分析(Set Pair Analysis),分析两个集合的联系度。

联系度，两个集合对其共有属性的相同、相异、相反的程度，用μ表示。

设两个集合A，B，通过集对分析联系度表示：

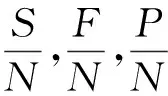
上式可以简写为

基本假设与合成公式：在一般情况下，把评委对论文的主观评分成绩记为A，把评委在评阅论文过程中出现的随机误差数记为B，则用联系数

U=A+Bi

表示评委对论文的真实评分值。

3 群组决策的论文名次集对分析模型建立

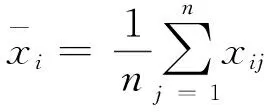
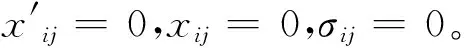
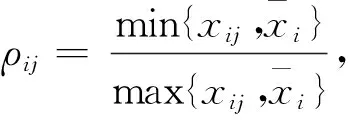
由集对分析理论及联系度的定义，取对立系数j=0，第i篇论文的最终得分可以用联系数μi，可表示为

在此基础上可以考虑随机误差对最终结果的影响，将上式整理合并为

(1)

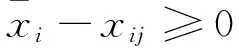
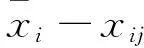
4 实例分析与比较

4.1 成绩的生成

由于竞赛论文数量众多而打分评委人数有限，在一定时间内评委无法实现一一打分，因此考虑先通过论文分配模型将论文合理分配给部分评委打分，利用评委赋权法进行初步评分排名。再将评选出来的前20份论文二次评分，二次评分可以实现评委对所有论文打分。在这种评分机制下考虑用集对分析模型来讨论排名的准确性，并与直接均值法，T分数法的排名做对比，说明用集对分析模型来解决论文排名的可实现性。

相关文献资料[11-14]显示，竞赛过程中考生成绩及每位评委的打分一般服从正态分布；文章为说明方法的可行性做了多次试验，试验中论文的客观成绩及各评委打分都来自于正态总体[15]，具体操作如下

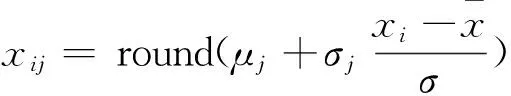
T分数法是将原始分数xij通过式(2)进行标准化处理转换成分数yij(称为T分数)，将T分数求均值进行排名的方法。

(2)

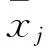
4.2 检验排名好坏的指标

按论文评分排名的结果为主观名次[4,5]，显然主观名次与客观名次越一致越好，因此通过定义重合度和乱序度作为本文排名方法好坏的指标。重合度指所有论文的主观名次与客观名次相同的个数；乱序度是所有论文的主观名次与客观名次差的绝对值之和。则论文的排名结果能使得重合度越高乱序度越小就越好。

4.3 具体实验及结果分析

每次实验的论文数m=20，参评评委数m=7，进行50次实验并将三种方法所得结果列表比较，见下表。

表1可以得到当论文数量较少，各评委对每份论文进行打分时，直接取均值法与集对分析法的效果相对较合理，T分数取均值法的排名结果误差较大。在实验过程中，直接取均值会出现不同论文打分均值相同的结果，影响最终排名；本文介绍的集对分析法从评委打分差异性和论文水平的不确定两方面考虑，更能反映论文成绩的真实水平。

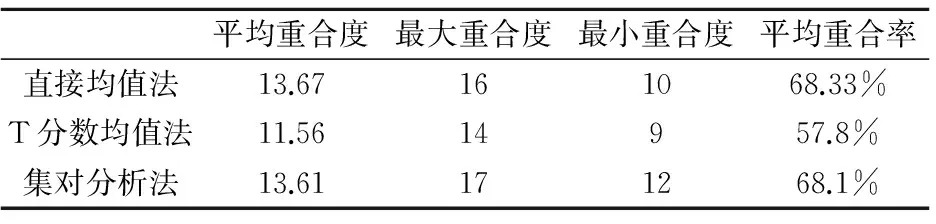
表1 50次实验结果分析Table 1 Analysis of 50 experimental results

评委根据评分标准对随机分配的论文进行打分，由表2可以看出评委3,7评分偏高，评委2,4评分偏低，其它评委评分适中。

表2 评委打分成绩Table2 Judgesscore表3 三种方法成绩与排名Table3 Theresultsandrankingsofthethreemethods

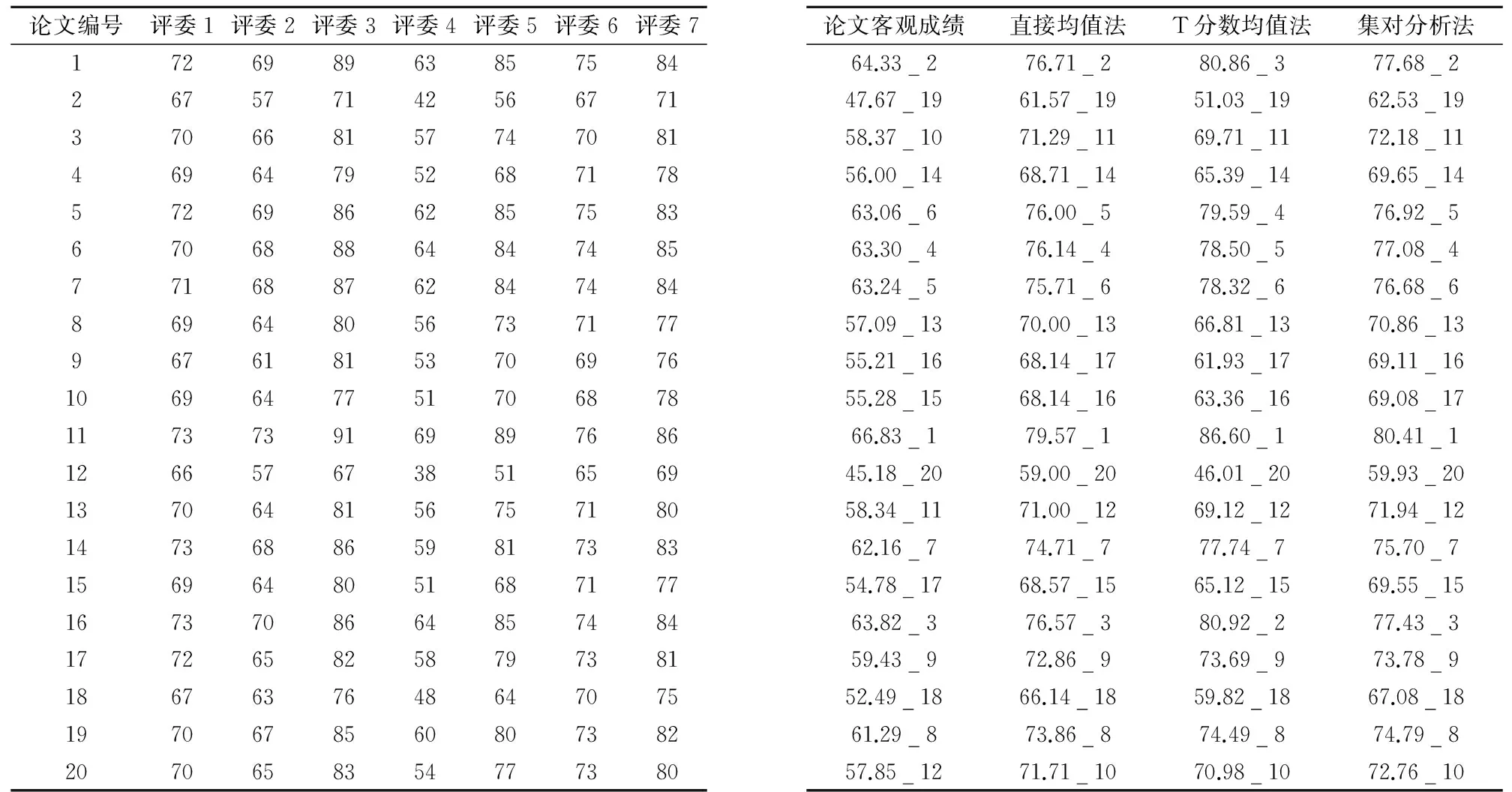
论文编号评委1评委2评委3评委4评委5评委6评委717269896385758426757714256677137066815774708146964795268717857269866285758367068886484748577168876284748486964805673717796761815370697610696477517068781173739169897686126657673851656913706481567571801473688659817383156964805168717716737086648574841772658258797381186763764864707519706785608073822070658354777380论文客观成绩直接均值法T分数均值法集对分析法64.33276.71280.86377.68247.671961.571951.031962.531958.371071.291169.711172.181156.001468.711465.391469.651463.06676.00579.59476.92563.30476.14478.50577.08463.24575.71678.32676.68657.091370.001366.811370.861355.211668.141761.931769.111655.281568.141663.361669.081766.83179.57186.60180.41145.182059.002046.012059.932058.341171.001269.121271.941262.16774.71777.74775.70754.781768.571565.121569.551563.82376.57380.92277.43359.43972.86973.69973.78952.491866.141859.821867.081861.29873.86874.49874.79857.851271.711070.981072.7610

注：s_r：表示论文成绩_名次。

表3显示依据表2评委打分情况，若直接求均值就缺少对评委评分差异的考虑，且会出现均分相等的情况；T分数法将各评委的评分价值坐标系统一，即将原始分经过变换使得各评委的均分相等以消除系统误差。运用集对分析模型考虑了评委评分的差异性，根据评委评分的差异系数(平均统一度)及差异部分对其打分偏高或偏低的习惯进行修正，排除了极端情况和人情分，使得该模型应用于评分排名更加客观，公正。该模型的排名与归一化的排名相差不大，因此集对分析模型解决排名问题的方法得以实现。

5 结束语

集对分析理论是一种基于辩证思维与数学方法有机结合的不确定性分析理论，它基于统一的确定与不确定系统，实现对不确定性问题完整和有效的分类与处理．本文建立的群组决策论文名次的集对分析模型考虑了论文水平的确定性与不确定性，以及评委打分过程中的随机性，运用集对分析理论有效处理了评委评分习惯的差异，提高了论文排名的准确性。

[1] KLEIN J. Assessing university students’ achievements by means of standard score (Z, score) and its effect on the learning climate[J]. Studies in Educational Evaluation, 2014,40:63-68.

[2] 易昆南,梁霞,易芳.缺损评分矩阵的论文排名[J].铁道科学与工程学报,2008,5(3):93-96.

[3] 易昆南.残缺数据的论文名次及评委水平的评判与逆判[J].湘潭大学学报(自然科学版),2005,27(2):39-43.

[4] 郭东威,丁根宏,毛俊诚,等.群决策论文型竞赛名次的加权T分数法[J].中国科技论文,2015(17):2059-2063.

[5] 郭东威,丁根宏,毛俊诚,等.确定专家权重的数量积法及在排名中的应用[J].烟台大学学报(自然科学与工程版),2015(4):249-254.

[6] 郭东威,丁根宏,毛俊诚,等.群决策论文名次的优化模型[J].统计与决策,2016(18):80-83.

[7] 史晓峰.基于多目标优化的竞赛评卷系统设计研究[D].哈尔滨：哈尔滨工业大学,2009.

[8] 鄢丽.公平的评卷系统[J].考试周刊,2007(44):4-5.

[9] 叶义成,柯丽华,黄德育.系统综合评价技术及其应用[M].北京：冶金工业出版社,2006.

[10] 赵克勤,宣爱理.集对论—一种新的不确定性理论方法与应用[J].系统工程,1996(1):18-23.

[11] 郑月锋,邢春波,黄德才,等.修正成绩为正态分布的一种新算法[J].统计与决策,2008(13):142-144.

[12] 尹向飞.基于混合正态分布的大学生考试成绩分布的拟合[J].统计与决策,2007(8):133-135.

[13] 徐明.正态分布应用于分数排位及调整的研究[D].上海：华东师范大学,2012.

[14] 李翔,冯珉,丁澍,等.考试成绩分布函数特点研究[J].中国科学技术大学学报,2011,41(6):531-534.

[15] LONGFORD N T. Reliability of essay rating and score adjustment[J]. Journal of Educational and Behavioral Statistics, 1993(3):31-48.