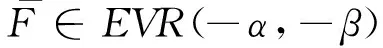基于客户到来的负二项风险模型的大偏差
2018-03-23孙歆,段誉
孙 歆, 段 誉
(贵州工程应用技术学院 理学院,贵州 毕节 551700)
1 模型建立
文献[1]和[2]讨论了广义复合二项风险模型,得到了该风险模型的索赔盈余的大偏差以及有限时间破产概率的Lundberg极限结果,其所讨论的风险模型如下:
(1)
(1)u>0为初始资金,c>0表示保险公司的保费额;
(2) {M(n);n=0,1,2,…}表示保险公司在[0,n]时间段内保费到达过程,是强度为λ>0的poisson过程,且M(n)=0;
(3) {N(n);n=0,1,2,…}表示保险公司在[0,n]时间段内理赔到达过程,是参数为(n,p)的二项随机序列,0 文献[3]将模型(1)中的索赔过程推广为负二项过程,同样得到了其索赔盈余的大偏差以及有限时间破产概率的Lundberg极限结果,但模型(1)讨论的是来自人群中同一类群的所有客户, 即该类客户从潜在索赔而言是不可辨别的,文献[4]讨论了基于客户到来的风险模型,是基于客户到来的个数,得到了其索赔盈余的大偏差,文献[5]将索赔过程推广为复合二项过程,得到了其索赔盈余的大偏差以及有限时间破产概率的Lundberg极限结果。文献[6]研究了连续时间和离散时间的基于客户到来风险模型,在一定假设下得到了其索赔盈余的大偏差以及有限时间破产概率的Lundberg极限结果。为了使模型更加符合保险公司的实际经营,近年来,越来越多的学者将随机变量的相依性引进了风险模型中, 见文献[7-11]等。 受上述文献的启示,我们讨论如下的风险模型: (2) 其中假设:(1)u>0为初始资金; (2) {N(n);n=0,1,2,…}表示保险公司在[0,n]时间段内的理赔到达过程,是参数为(n,p)的负二项随机序列,0 (3)在时刻σk,第k个客户购买了保单,保险公司因此在一定时期内担负了来自该保单的风险。设来自第k个客户的潜在索赔额为Bk,对每一个k≥1,Bernonlli随机变量Ik表示第k份保单是否真正发生索赔(Ik=0表示没有发生索赔,Ik=1表示发生索赔); (4) {Bk;k≥1}是一列非负同分布的延拓负相依随机变量序列,其分布函数为F(x),期望为μ<∞,{Ik;k≥1}是一列非负同分布的延拓负相依Bernonlli随机变量序列,且P(Ik=1)=θ,P(Ik=0)=1-θ; (5)假设{N(n);n=0,1,2,…},{Bk;k≥1}和{Ik;k≥1}相互独立。每份保单的保费假设是(1+ρ)μ,常数ρ可解释为安全负载系数。因此保险公司来自第k份保单的净索赔额为 BkIk-(1+ρ)μ, 从而保险公司的潜在总损失额为 (3) 潜在总索赔额为 (4) 定义T(u)=inf{n;R(n)<0}=inf{n;S(n)>u}为模型(2)的破产时刻,设T>0,定义初始资金为u的有限时间破产概率为 ψ(u,T)=P(T(u)≤T)。 下面是经常用到的几个重尾分布族。 定义2[8]若存在常数M>0,对于任意的n=1,2,…及任意的n个实数x1,x2,…,xn,使得 同时成立,则称随机变量序列{Xk,k≥1}是延拓负相依的。特别的当M=1时称随机变量序列{Xk,k≥1}是负相依的。 关于x≥γn一致成立。 (i)对任意的x>0,y>0,β满足引理2,则有 其中max{x,y}表示实数x,y两者中的最大者。 (ii)对任意的0 注:若P(Ik=1)=θ=1,且满足模型(1)中给出的条件(5),则定理1就为[3]中的引理1的结论。 证明:对任意的n≥2,任意的xk≥0,ak=1或0,k=1,2,…n。我们有 P(B1I1≤x1,B2I2≤x2,…,BnIn≤xn) =P(B1a1≤x1,B2a2≤x2,…,Bnan≤xn)P(I1=a1,I2=a2,…,In=an) 其中M1>0,M2>0,M=M1M2>0,类似可证: P(B1I1>x1,B2I2>x2,…,BnIn>xn)≤MP(BiIi>xi)。 关于x≥γn一致成立,即 关于x≥γn一致成立。 定理2的证明: (i) 对任意的x>0,y>0,由定理1,对任意的0<δ<1,当u→∞时,一致有 P(T(u)≤yux)≥P(S([yux])>u)=P(S([yux])-ES([yux])>u-ES([yux])) ~P(S([yux])-ES([yux])>u+(1+ρ-θ)μp[yux]) ≥P(S([yux])-ES([yux])>u+(1+ρ)μp[yux]) 其中[y]表示实数y的取整函数,因此,对1<β<∞,由引理2得, ≥x-βmax{1,x}。 所以(i)得证。 (ii) 设0 由引理2得, 所以定理2得证。 [1] HU Y J. Finite time ruin probabilities and Large deviations for generalized compound binomial risk models[J]. Acta Mathematica Sinica(English Series), 2005,21(5):1099-1106. [2] KONG F C, ZHAO P. Some large deviation results for generalized compound binomial risk models[J]. Journal of mathematical research and exposition,2009,29(6):1047-1053. [3] KONG F C, SHEN C. Large deviation results for generalized compound negative binomial risk model[J]. Acta Mathematica Sinica, English Series, 2009,1(25):151-158. [4] NG KW, TANG QH, YAN JA, et al. Precise large deviations for the prospective-loss process[J]. Journal of Applied Probability, 2003,40(2):391-400. [5] 马学敏,胡亦钧.复合二项过程风险模型的精细大偏差及有限时间破产概率[J].数学学报,2008,51(6):1199-1130. [6] MA X M. Precise large deviations for a customer-based individual risk model[J]. Acta Mathematica Sinica(English Series), 2011,27(2):209-222. [7] CHEN Y, YUEN K C, NG K W. Precise large deviations of random sums in presence of negative dependence and consistent variation[J]. Methodology and Computing in Applied Probability,2011,4(13):821-833. [8] YANG Y, LEIPUS R,IAULYS J. Precise large deviations for actual aggregate loss process in a dependent compound customer-arrival-based insurance risk model[J]. Lithuanian Mathematical Journal, 2013,53(4):448-470. [9] 马秀芬.相依索赔下基于客户来到风险模型的渐近性质[D].兰州:西北师范大学,2013. [10] TANG F Q, BAI J M. Precise large deviations for aggregate loss process in a multi-risk model[J]. Journal of the Korean Mathematical Society, 2015,3(52):447-467. [11] LIU L. Precise large deviations for dependent random variables with heavy tails[J]. Statistics and Probability Letters, 2009,79(9):1290-1298.

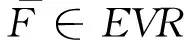
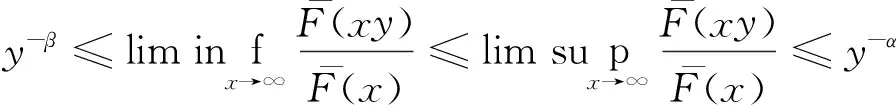

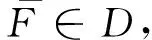


2 主要结论


3 相关引理和定理证明




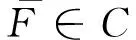
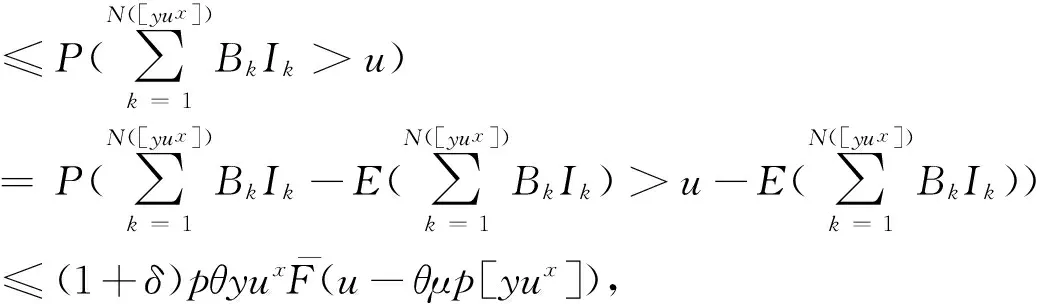

4 结论