已知平面与高程点不同时的严密三维基准变换

曹 旭,沈云中

(同济大学 测绘与地理信息学院，上海 200092)

在GNSS测量工程应用中经常需要进行三维基准转换[1]。根据旋转与尺度参考点的不同定义，三维坐标转换模型：Bursa-Wolf模型、Molodensky模型及武测模型等[2]。传统的三维坐标转换模型只考虑了公共点的一套坐标误差，对另一套坐标误差不予考虑，利用线性或非线性坐标转换模型进行解算[3-7]。同时，诸多学者也对整体最小二乘的解法进行了研究[8-10]。文献[11]提出顾及两套坐标误差的Bursa模型坐标变换方法，基于公共点两套坐标改正数加权平方和最小为准则解算转换参数，根据公共点与转换点间的互协方差阵，利用公共点坐标的改正数推估出转换点坐标的改正数，显著提高了坐标转换精度。文献[12]提出无缝三维基准转换模型，同时考虑公共点的两套坐标误差和转换点的坐标误差，将计算转换参数和变换转换点坐标联合处理，坐标精度得到进一步改善。文献[13]针对常规控制网平面和高程控制网分开布设的特点，利用过渡坐标系改进了三维坐标变换模型，并不需要三维已知点，分别利用常规控制网的平面坐标和高程解算7个转换参数。

本文基于平面和高程控制网分开布设的实际情况，同时顾及两套坐标都存在误差，导出相应的基准变换参数解算模型，并用算例说明了本文模型的优点。

1 三维基准变换模型

当坐标旋转角是小角度时，三维基准变换的Bursa模型[14]：

(1)

其中，TX，TY和TZ为三个平移参数，ωX，ωY和ωZ是三个旋转参数，k为尺度参数；[XiYiZi]T为第i点的三维坐标，上标I和II表示两套坐标系。

当旋转和尺度参数相对于参考点K时，称为Molodensky模型[13]，其变换为

(2)

其中，[ΔXKiΔYKiΔZKi]T=[Xi-XKYi-YKZi-ZK]T。

文献[13]提出将原有的坐标系先绕Z轴逆时针旋转Li角，再绕Y轴顺时针旋转90°+Bi角，最后Z轴反向，得到过渡坐标系O-xyz，其中，Li和Bi为平面坐标与高程分开的那个坐标系的第i点的经度与纬度。变换的旋转矩阵：

在式(2)两边同时左乘Ri，可得

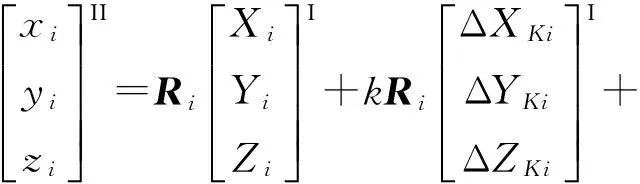
(3)

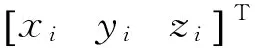
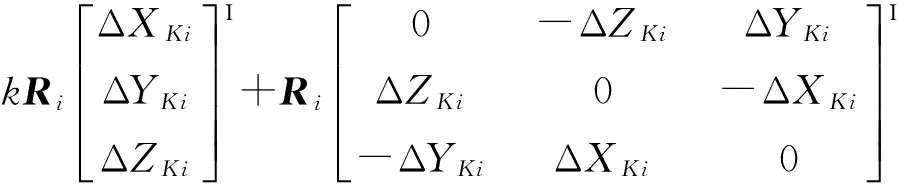
(4)

其向量和矩阵形式为

(5)

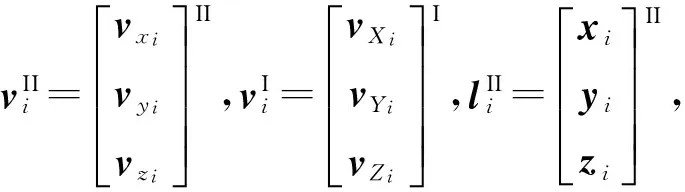
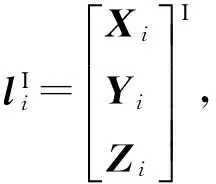
Ai=

对于平面控制点，只选取式(4)中的前两个方程；对于高程控制点，只选取式(4)中的第三个方程。

2 基准变换参数的解算模型

如果有n个公共点，其编号从1～n，则其误差方程为

VII-RVI=Aξ-(LII-RLI).

(6)

2ST(VII-RVI-Aξ+LII-RLI)=min.

(7)

其中，S为联系数向量，Q11,I为公共点的GNSS控制网坐标系下的协因数阵，Q11,II为平面与高程分开布设的公共点对应的传统控制网坐标系下的协因数阵。分别对残差向量VI，VII和参数向量ξ求一阶导数，并令其为零，得

(8)

由式(8)前两式得

RVI=-RQ11,IRTS，VII=Q11,IIS.

(9)

两式相减得

VII-RVI=(RQ11,IRT+Q11,II)S.

(10)

将其代入式(6)，得

S=(RQ11,IRT+Q11,II)-1

(Aξ-LII+RLI).

(11)

将式(11)代入式(8)中第三个方程，得

AT(RQ11,IRT+Q11,II)-1Aξ=

AT(RQ11,IRT+Q11,II)-1(LII-RLI).

(12)

所以，平面与高程分开布设的顾及两套坐标误差的三维基准变换的转换参数解为

AT(RQ11,IRT+Q11,II)-1(LII-RLI).

(13)

由式(13)可以解出转换参数后，代入式(11)计算联系数向量S后，再由式(9)计算改正数向量VI和VII。因R是正交矩阵，式(9)的左式也可表示为

VI=-Q11,IRTS.

(14)

V2,I=Q21,I(Q11,I)-1VI.

(15)

利用式(15)对第一套GNSS控制网转换点坐标进行改正，并用得到的转换参数转换改正后的转换点，得到转换点在另一套坐标系下的坐标，即常规控制网坐标。

3 算例分析

先模拟18个点的一套GNSS坐标，给定一组转换参数ξ=[1 000 m 2 000 m 3 000 m 6.43″ 5.12″ 4.89″ 1.000 01]，参考点K的坐标为(-1 240 000.000，4 990 000.000，3 760 000.000)，采用Molodensky模型计算出18个点的转换后坐标，转换前后的部分坐标如表1所示，再按克拉索夫斯基椭球参数，中央子午线104°投影得到平面坐标和大地高，利用EGM2008模型计算出高程异常后求得18个点的正常高。为了说明本文变换模型的优越性，选取1～8号点作为公共点，其中1～3号点为常规平面控制网，4～8号点为常规高程控制网。

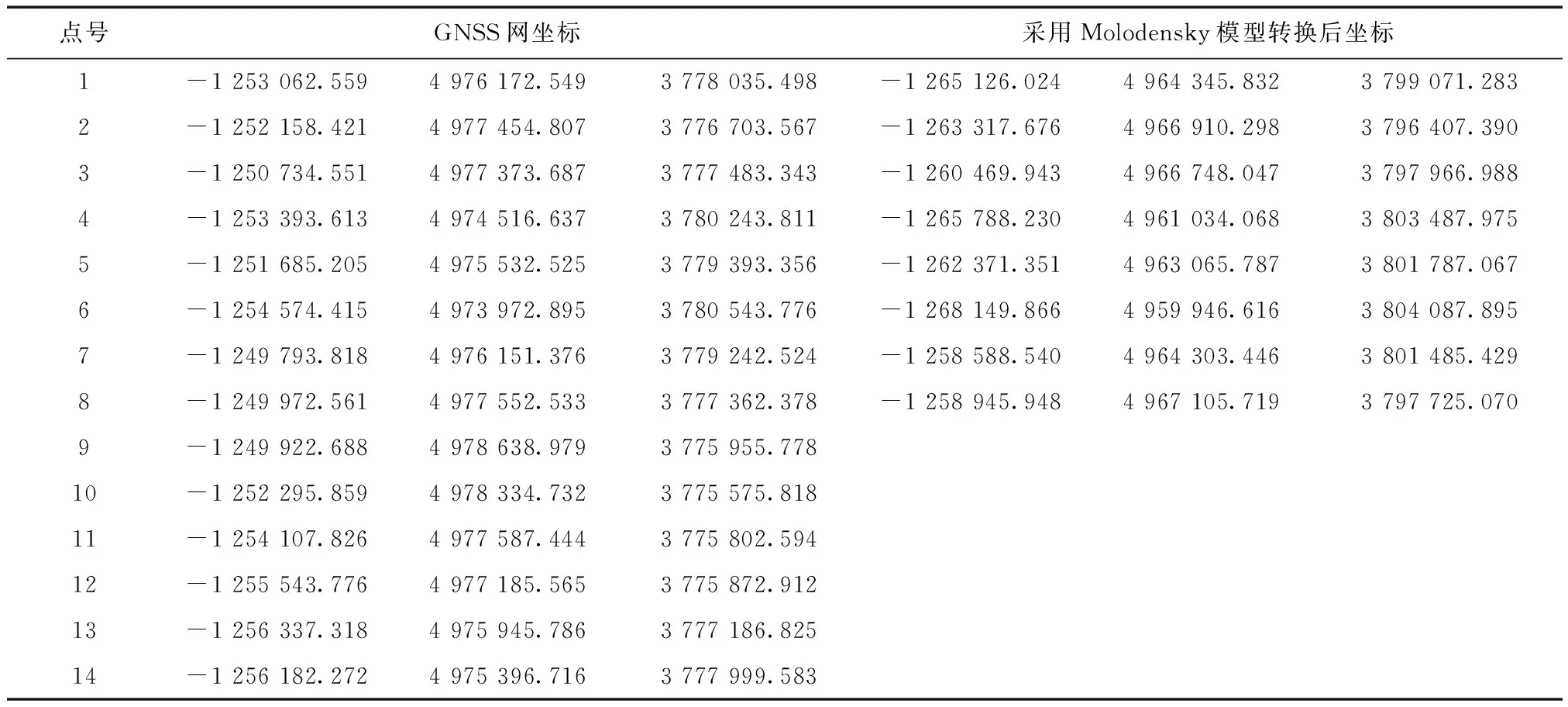
表1 公共点与转换点的坐标 m

续表1

对于常规控制网的平面网，其平面坐标x和y均模拟标准差为5 mm，相关系数为0.3的随机误差，不同点之间误差的相关系数为0.2；高程模拟5 mm的误差，不同点的相关系数也是0.2。对于转换前的坐标(通常是GNSS控制网的坐标)，其X,Y,Z坐标均模拟8 mm的误差，且各坐标分量的相关系数为0.3，不同点之间的相关系数为0.15。比较本文三维基准转换模型与传统模型的坐标转换效果，设计两种方案：

方案一：对于传统基准转换模型的矩阵形式

l-el=Aξ.

采用传统方法，即基准变换模型只考虑公共点的第二套坐标误差。此时，根据间接平差原理，可解得转换参数为

(16)

再由此参数对转换点进行变换；

方案二：采用本文平面与高程点不同时的严密三维基准变换方法。

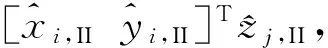
(17)

以及转换点的平面精度

(18)

模拟数据计算1 000次，得到两种方案转换点坐标变换精度如图1和图2所示。方案一4个平面点(912号点)的平均平面变换精度为5.0 mm，方案二为4.2 mm；方案一6个高程点(1318号点)的平均高程变换精度为5.4 mm,方案二为3.9 mm。结果表明：采用本文平面与高程点不同时的严密三维基准变换方法能够改善坐标转换精度。

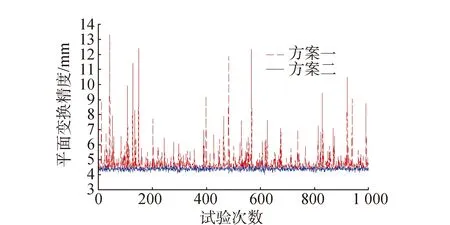
图1 方案一(虚线)与方案二(实线)的平面变换精度比较

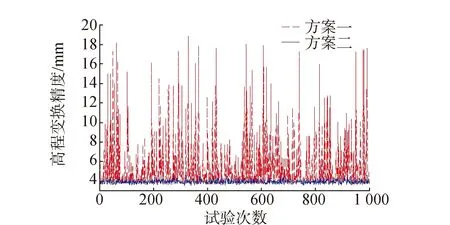
图2 方案一(虚线)与方案二(实线)的高程变换精度比较

4 结 论

本文的基准变换方法适用于常规控制网的高程与平面网分开布设的情况，同时考虑到两套坐标都含有误差，利用分离的平面坐标和高程值直接解算转换参数，对转换点的坐标进行改正，模拟数据的分析结果表明，本文方法能够有效地提高转换结果的精度，实现与GNSS三维控制网的基准变换，得到结论：

1)当常规控制网的平面控制点没有高程值或高程控制点没有平面坐标时，采用本文方法可以直接解算转换参数，不需要计算获得控制点完整的三维坐标，避免出现误差传递，提高解算精度。

2)与传统基准变换模型相比，本文方法考虑两套坐标误差的影响，对转换点坐标进行改正，提高基准变换的精度。

[1] YANG Y X.Robust Estimation of Geodetic Datum Transformation[J].Journal of Geodesy.1999,73:268-274.

[2] 刘大杰. 全球定位系统(GPS)的原理与数据处理[M]. 上海：同济大学出版社, 1996.

[3] 陈义，沈云中，刘大杰.适用于大旋转角的三维基准转换的一种简便模型[J].武汉大学学报(信息科学版)，2004,29:1101-1104.

[4] 杨元喜，徐天河.不同坐标系综合变换法[J].武汉大学学报(信息科学版)，2001,26(3):509-513.

[5] 吕志平，乔书波.大地测量学基础[M].北京：测绘出版社，2011.

[6] 袁庆，楼立志，陈玮娴.加权总体最小二乘在三维基准转换中的应用[J].测绘学报，2011,40(增1)：115-119.

[7] 曾怀恩，黄声享.三维坐标转换参数求解的一种直接搜索法[J].武汉大学学报(信息科学版)，2008,33(11)：1118-1121.

[8] 葛旭明, 伍吉仓. 三维基准转换的约束加权混合整体最小二乘的迭代解法[J]. 武汉大学学报(信息科学版)，2012, 37(2):178-182.

[9] 杨仕平, 范东明, 龙玉春. 基于整体最小二乘法的任意旋转角度三维坐标转换[J]. 大地测量与地球动力，2013, 33(2):114-119.

[10] SHEN Y Z, LI B F, CHEN Y. An iterative solution of weighted total least-squares adjustment[J]. Journal of Geodesy. 2011, 85(4):229-238.

[11] 李微晓，沈云中，李博峰.顾及两套坐标误差的三维坐标转换[J].同济大学学报(自然科学版)，2011,39:1243-1246.

[12] 李博峰，沈云中，李微晓.无缝三维基准转换模型[J].中国科学，2012,42(7):1047-1054.

[13] 沈云中，卫刚.利用过渡坐标系改进3维坐标变换模型[J].测绘学报，1998,27:161-165.

[14] 刘大杰.大地坐标转换与GPS控制网平差计算及软件系统[M].上海：同济大学出版社，1997.

[15] SCHAFFRIN B.TLS collocation: the Total Least Squares Approach to EIV-Models with stochastic prior information[J]. Presented at the 18th International Workshop on Matrices and Statistics, Smolenice Castle, Slovakia,2009.