天线相位中心改正对GPS精密单点定位的影响

张 磊，兰孝奇，房成贺，张崇军

(河海大学 地球科学与工程学院，江苏 南京 210098)

IGS提供基于卫星的质量中心的高精度的卫星轨道和卫星钟差，而观测值是基于卫星的相位中心，因此只有知道卫星和接收机的精确相位中心位置，才能提高定位的精度[1]。天线相位中心改正通常由以下两个部分组成：一部分是天线相位中心偏差(Phase Center Offset,PCO)，该部分误差是由天线平均相位中心与天线参考点之间偏差导致而成；另一部分是天线相位中心变化(Phase Center Variation,PCV)，该部分误差是由天线瞬时相位中心与平均相位中心之间的偏差导致而成[2]。自1998年开始，IGS采用相对天线相位中心模型IGS_01，该模型假定参考天线的PCV值为0。而参考天线的实际PCV值并不为0，尤其是参考天线的PCV值会随着高度角的变化而变化，PCV影响可达到数厘米，这样定位的精度便难以保证[3]。从2006-11-05(GPS周为1400)起，IGS采用绝对天线相位中心模型IGS_05，该模型不仅考虑PCO，还考虑PCV，大大提高定位的精度[4]。国内，朱智勤、张小红等分析了相位中心模型转变对定位精度的影响，表明绝对相位模型在高程方向精度提高明显[5]。郭际明等改化了GPS天线相位中心算法，表明天线相位中心变化不影响水平方向的定位结果，只影响高程方向的定位结果[6]。刘慧娟、吴正等人设计了多种方案研究GPS天线相位中心改正，实验结果表明天线相位中心偏差对精密单点定位有不同程度的影响，尤其是天线相位中心偏差PCO在高精度定位时不能忽略[8-9]。宗玉玉等人分析了卫星、接收机天线相位中心改正(PCO)和相位中心偏差(PCV)对精密单点定位的影响，天线相位中心改正对平面精度影响小，对高程精度影响大，可达5～10 cm；相位中心偏差对定位影响相对较小，在高程方向影响也能达到几厘米[10]。

本文比较了不同天线相位中心改正模型，研究了卫星和接收机PCO，PCV对定位精度的影响，利用IGS_05模型对天线相位中心改正进行估计，分析PCO和PCV对定位精度的影响，并提出改正方法。

1 天线相位中心改正原理

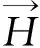
(1)

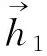
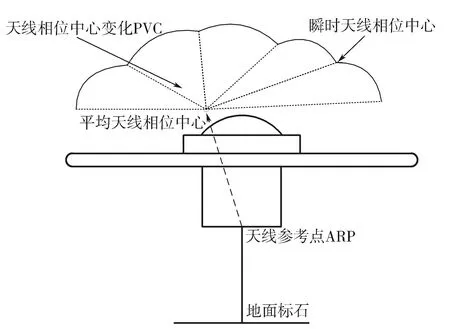
图1 天线相位中心改正示意图

绝对天线相位中心改正为[8]

Δφ(α,z)=Δφ′(α,z)+Δr×e.

(2)

式中：α为卫星信号的方位角；z有两种意义：第一种z表示为GPS接收机的天顶角，第二种z表示为GPS卫星的天底角(nadir angle)；Δφ(α,z)为α及z方向的总的改正量；Δr表示平均天线相位中心至ARP的距离；e定义了一个卫星与接收机方向上的旋转矩阵；Δφ′(α,z)表示天线相位中心变化的改正值。

2 天线相位改正模型

目前，IGS可提供两种天线相位改正模型：一种是相对天线相位中心IGS_01改正模型；另一种是绝对天线相位中心IGS_05改正模型，表1显示了两种模型的异同。

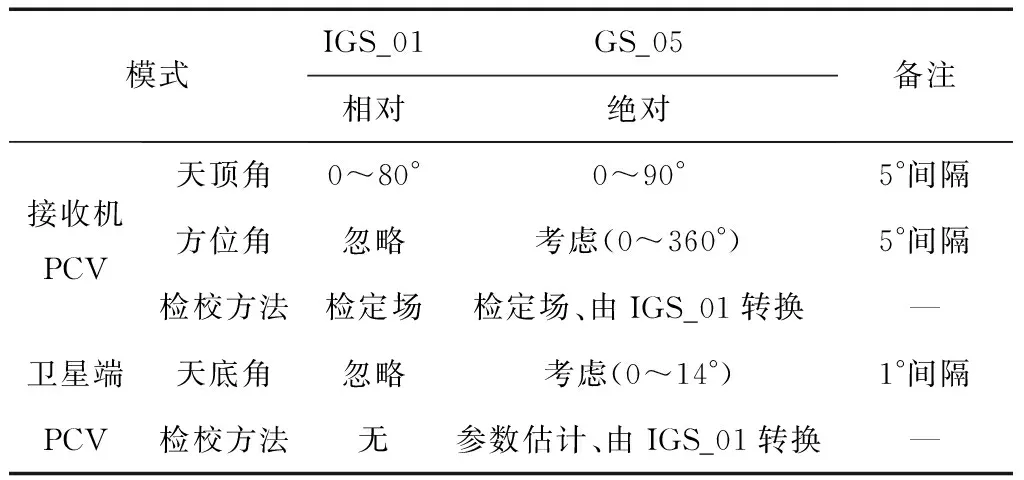
表1 IGS_01与IGS_05模型比较

从表1中可以看出，IGS_01模型只考虑卫星高度角为0～80°时，接收机PCV随卫星高度角变化，但是信号入射方位角对PCV值的影响却没有考虑。而且，卫星端PCV在IGS模型中也没有考虑。与相对天线相位改正模型相比，绝对天线相位改正模型不仅考虑了天顶角和方位角的变化对接收机PCV值的影响，而且还顾及了接收机的PCV值。由此可知，采用绝对天线相位模型可以消除定位系统误差，进而可以提高精密单点定位的精度。

2.1 天线相位中心偏移(PCO)

接收机的PCO是在局部站心坐标系中，该坐标系以ARP为原点，而IGS提供的天线PCO是在星固坐标系下。因此，为计算PCO改正后卫星的位置，需先将天线PCO改正至星固坐标系下，设该方向的单位向量

(3)

式中：Xsat是卫星质量中心在ECEF系中的坐标；Xsun是太阳坐标。星固系中，其原点在卫星质心，Z轴指向地球质心，Z轴的单位向量ez可表示为

(4)

星固系中Y轴方向比较特殊，其方向与卫星方向与太阳方向至卫星方向的向量积方向相同，Y轴方向的单位向量ey为

ey=ez×e.

(5)

星固系中X轴与上述Y轴、Z轴构成右手系，其单位向量ex为

ex=ey×ez.

(6)

卫星天线平均PCO改正为

(7)

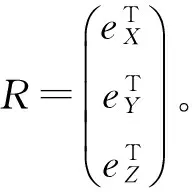
与卫星天线PCO改正类似，接收机天线PCO改正也需将站心坐标系中PCO转换至地固系中，再用式(2)计算总改正量。

2.2 天线相位中心变化量(PCV)

如图2中所示，天线相位中心并不是固定不变的，而是随时间的变化而变化的，天线PCV便是天线平均相位中心与天线瞬时相位中心的差值。IGS提供的接收机天线相位中心不仅随着接收机的天底角变化，而且会随着接收机的方位角变化。

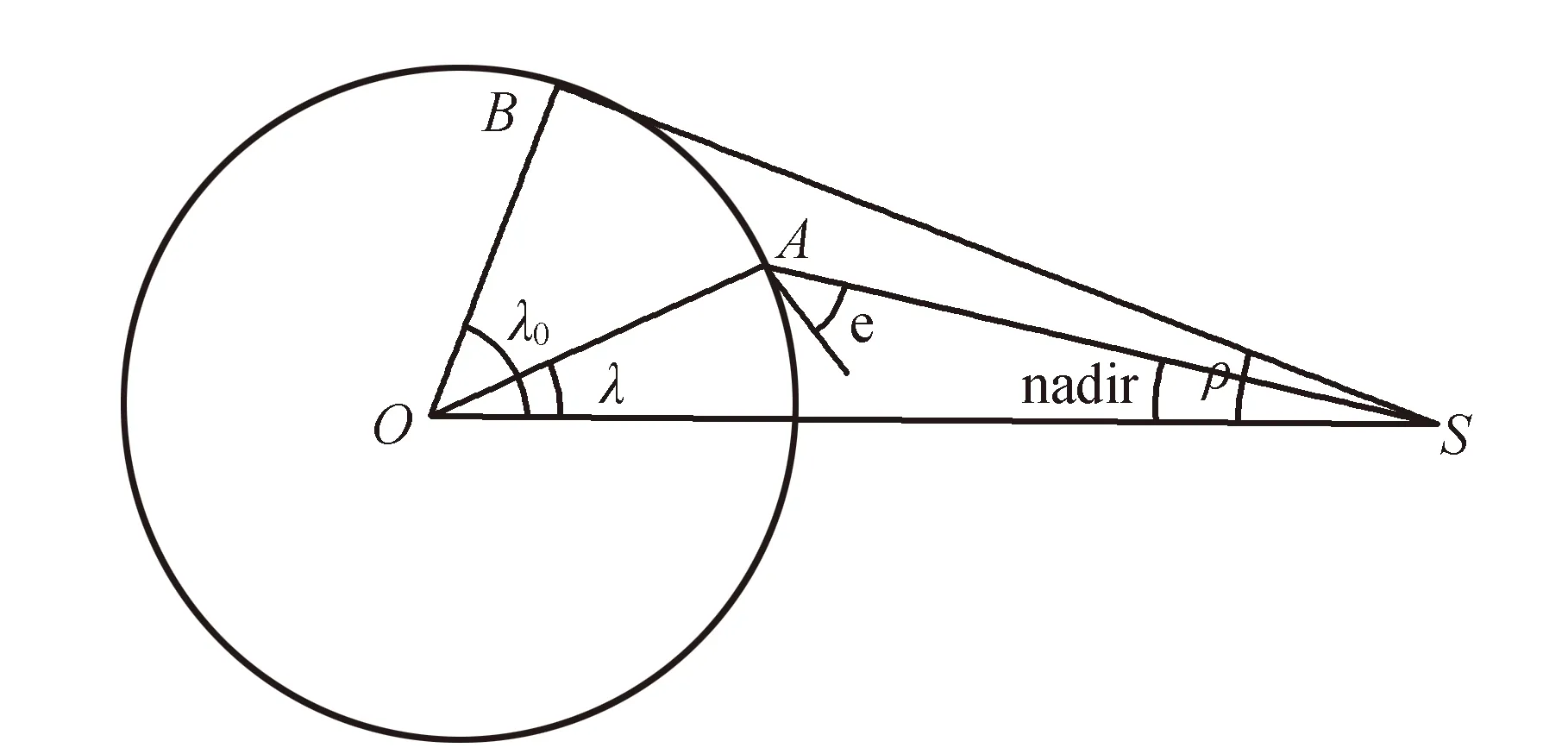
图2 PCO改正前后与坐标真值的偏差

图中，用户A至卫星S的距离为R；地球半径为Rearth；卫星高度角为e；天底角为nadir。在三角形OAS中，由正弦定理可得

(8)

式中：OS=Rearth+R，OA=Rearth，卫星的天底角nadir可由式(8)计算可知。IGS提供的1°间隔的卫星PCV改正值，用户可根据改正值，利用线性内插的方法求出天底角对应的PCV值。

接收机PCV与卫星PCV计算过程类似，但接收机PCV还要考虑接收机方位角的变化。目前，IGS提供了所有类型接收机PCV改正值，以5°的间隔给出[9]。因此，为求出待定点的PCV值，可利用分段线性插值计算，计算原理如图3所示。

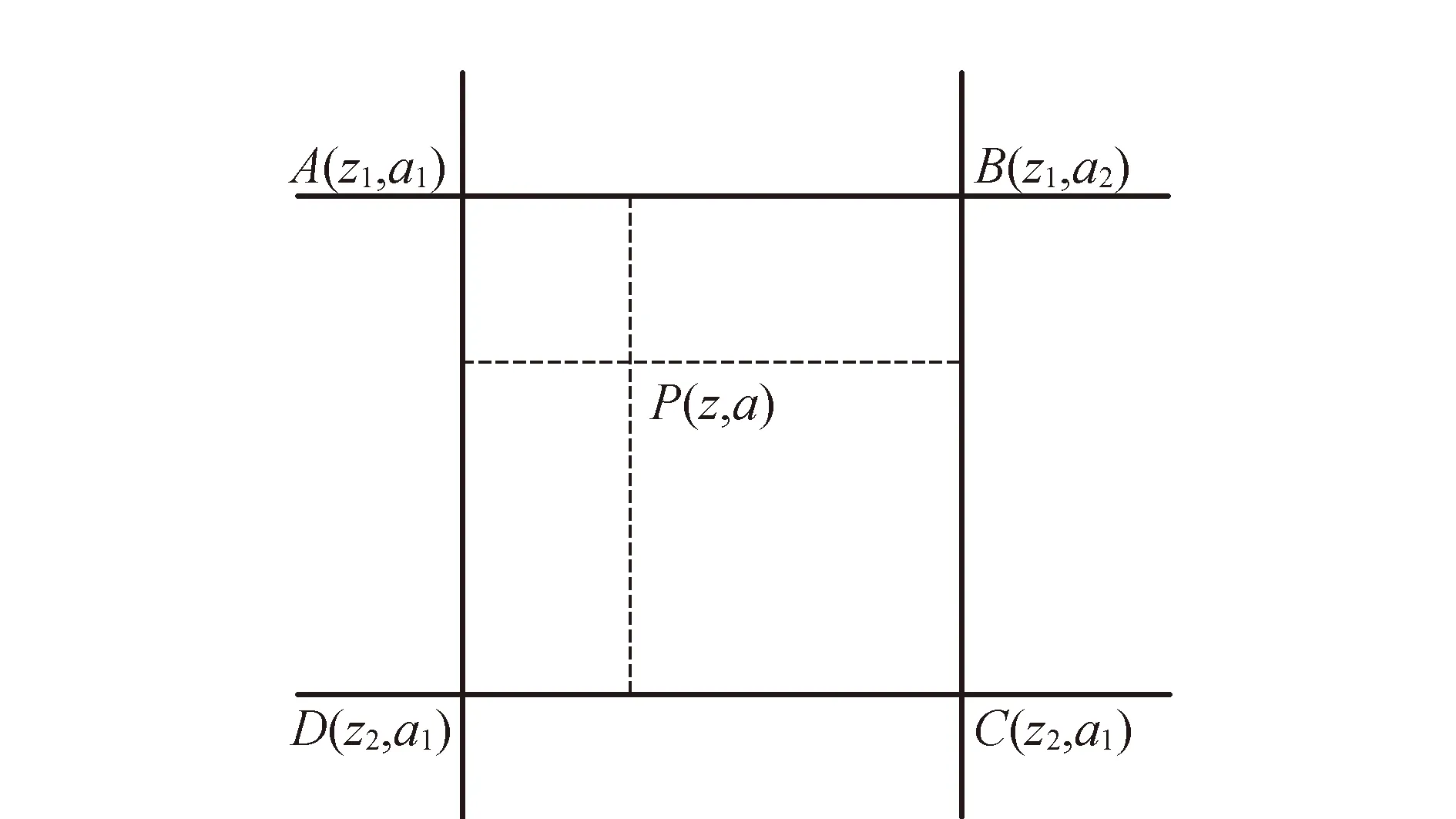
图3 PCV插值示意图

如图3所示，点A与点B具有相同的高度角，点A与点D具有相同的方位角。假设点P的高度角和方位角位于ABCD组成的网格中，P的PCV值采用线性内插得到

PCVP=(1-α)(1-β)PCVA+α(1-β)

PCVB+αβPCVC+(1-α)βPCVD.

(9)

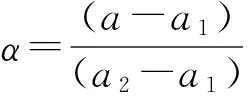
3 算例分析

实验数据采用4个IGS站(BJFS、MADR、ALBH、FAIR)2014-07-16的观测数据，并下载对应的天线改正文件和卫星星历钟差文件。为比较绝对定位模型和相对定位模型，以及PCO，PCV对精密单点定位的影响，本文从以下几个方面加以说明。

3.1 不同改正模型对定位精度的影响

为了比较不同的改正模型对定位精度的影响，本文设计方案1和方案2进行对比。

方案1：采用相对相位中心模型改正。

方案2：采用绝对相位中心模型改正，而不考虑接收机天线相位模型改正。

为检验定位结果，本文以IGS公布的当天坐标为真值，各测站方案1与方案2的精密单点定位结果与真值在N，E，U方向的偏差如表2所示。

表2 不同改正模型对定位的影响 m

从表2中可以看出，方案1的精度较方案2的精度要低，但是在平面方向上精度提高较少，但是在高程方向上提高较大，高程方向的精度可提高1 cm。

3.2 卫星天线相位中心偏差对精密单点定位精度的影响

在采用绝对天线相位模型改正后，设计方案3和方案4比较卫星天线相位中心对精密单点定位精度的影响。

方案3：所有测站都进行卫星PCO改正。

方案4：在所有测站都进行卫星PCO改正的基础上，进行卫星PCV改正。

方案3与方案4得出的各测站的精密单点定位结果在N，E，U方向与真值的偏差如表3所示。

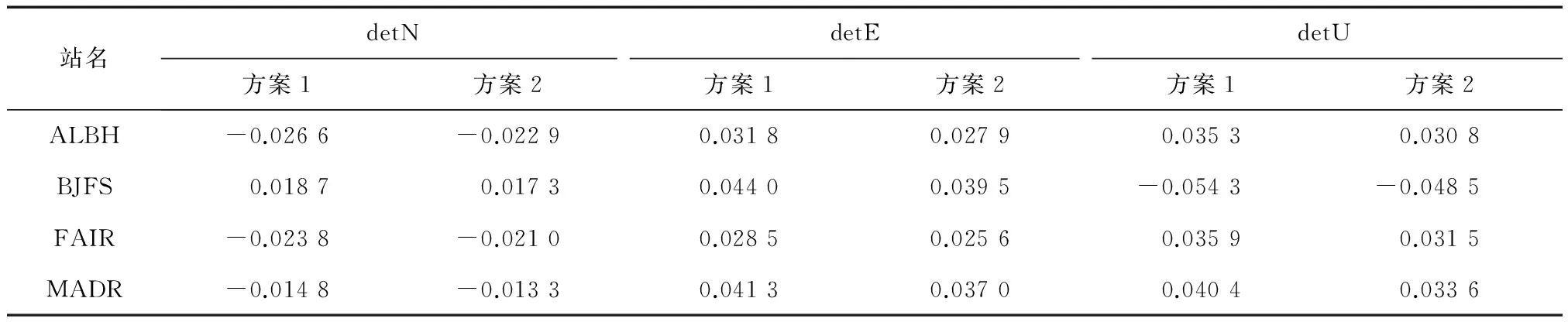
表3 卫星天线相位中心对定位的影响 m

从表3中可以看出，在绝对天线相位模型改正后，再进行卫星PCO以及PCV改正，定位精度又有所提高。但是卫星相位中心变化在平面方向上精度提高有限，基本都在2 mm左右；而在高程方向精度提高稍大，可达4～5 mm。除此之外，可以看出卫星PCO对定位的影响比卫星PCV的影响大。

3.3 接收机天线相位中心偏差对精密单点定位精度的影响

在绝对天线模型改正基础上，进行卫星天线相位中心改正后，设计方案5和方案6，比较接收机天线相位中心对精密单点定位精度的影响。

方案5：所有测站都进行接收机PCO改正。

方案6：在所有测站都进行接收机PCO改正的基础上，进行接收机PCV改正。

方案5与方案6得出的各测站的精密单点定位结果在N，E，U方向与真值的偏差如表4所示。

从表4中可看出，在卫星天线相位中心改正后，再进行接收机PCO以及PCV改正，定位精度又提高稍许。但是平面方向精度提高较少，只有1 mm左右；高程方向精度提高略微大些，达到3 mm。

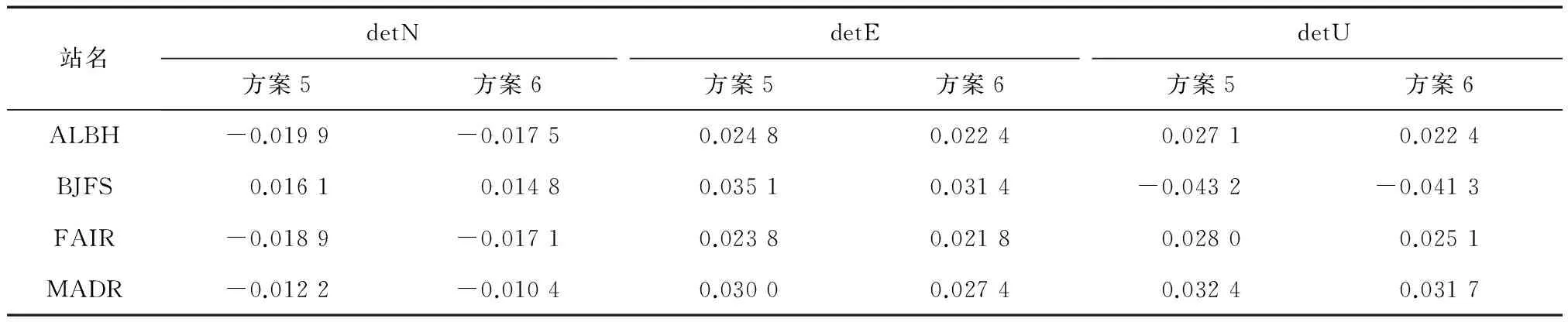
表4 接收机天线相位中心对定位的影响 m

4 结 论

本文分析了不同相位中心改正模型对定位精度的影响，并讨论卫星和接收机PCO,PCV对定位精度的影响，得出以下结论：

1)与相对相位中心改正模型相比，绝对相位中心改正模型精度有一定提高，在平面方向提高有限，只有毫米级，但在高程方向提高较大，可达到1 cm。

2)在精密单点定位中，PCO和PCV对定位精度有一定程度的影响，在平面方向影响较小，但在高程方向影响较大，可达到厘米级。

3)卫星和接收机PCV对定位影响较小，在高程方向仅带来几毫米的误差；而卫星和接收机PCO对定位影响较大，在高程方向影响可达及厘米。

4)与卫星的PCO和PCV相比，接收机PCO和PCV相对较少，说明与卫星天线相位中心相比，接收机天线相位中心对精密单点定位影响更小。

[1] 郝明, 丁希杰. GPS精密单点定位的数据处理方法综述[J]. 测绘工程, 2008, 17(5):60-62.

[2] 李征航. GPS测量与数据处理[M]. 武汉：武汉大学出版社, 2005.

[3] SCHUPLER B R, CLARK T A, ALLSHOUSE R L. Characterizations of GPS User Antennas: Reanalysis and New Results[M]// GPS Trends in Precise Terrestrial, Airborne, and Spaceborne Applications. Springer Berlin Heidelberg, 1996:328-332.

[4] 涂锐, 黄观文, 邹顺. 天线相位中心偏差变化及改正模型对精密单点定位精度的影响[J]. 大地测量与地球动力学, 2010, 30(3):113-117.

[5] 张小红, 李盼, 李星星,等. 天线相位中心改正模型对PPP参数估计的影响[J]. 武汉大学学报(信息科学版), 2011, 36(12):1470-1473.

[6] 郭际明, 史俊波, 汪伟. 天线相位中心偏移和变化对高精度GPS数据处理的影响[J]. 武汉大学学报(信息科学版), 2007, 32(12):1143-1146.

[7] 刘慧娟, 党亚民, 王潜心. GPS天线相位中心改正及其影响分析[J]. 导航定位学报, 2013, 1(2):29-33.

[8] 吴正, 胡友健, 敖敏思,等. GPS天线相位中心改正方法研究[J]. 地理空间信息, 2012(6):56-58.

[9] 胡志刚, 赵齐乐, 郭靖,等. GPS天线相位中心校正对低轨卫星精密定轨的影响研究[J]. 测绘学报, 2011, 40(增1):34-38.

[10] 宗玉玉, 段兵兵, 蔡东健. 天线相位中心改正对定位参数的影响[J]. 工程勘察, 2015, 43(1)：65-68.