一种改进遗传神经网络的建筑基坑沉降预测模型

2018-03-20周星勇杨容浩王志胜冉中鑫

测绘工程 2018年3期

周星勇，杨容浩，王志胜，冉中鑫

(成都理工大学地球科学学院，四川成都 610059)

随着我国现代化和城市化进程的不断加快，基础设施工程建设规模和数量不断增加，基坑开挖深度和广度也不断提高。因此，对于沉降监测、预报的要求越来越高[1]。针对基础设施工程中的变形预测，国内外学者已经开展了许多相应的研究。主要的预测方法有回归分析法、时间序列分析[2]、灰色系统理论、卡尔曼滤波预测模型[3]和BP神经网络[4-5]等。其中，BP神经网络由于具有强大的自学习能力，能够对复杂的工程形变问题进行建模，并模拟变形的发展规律，达到形变预测的目的，受到广泛的关注和研究[6]。

由于易受初始权值和阈值的影响而陷入局部最优值，利用BP神经网络进行基坑变形预测，并不能保证每次都得到理想的效果。为了提高BP神经网络基坑变形预测的有效性和预测精度，许多学者开展了BP算法的改进研究。常见的改进算法有基于粒子群算法优化的BP算法[7]、AFSA算法优化BP神经网络[8]、小波神经网络[9-10]、灰色神经网络[11]、模拟退火算法优化BP神经网络[12]、遗传神经网络[13]等。但这些算法对监测数据无法连续获取，或监测数据中含有一定粗差的情况并不能取得满意效果[14]。本文引入自适应增强算法，对遗传神经网络预测模型进行优化，通过自适应增强算法整合多个GA-BP弱预测器，最终能达到提高基坑沉降量预测精度和稳定性目的。

1 GA-BP神经网络

1.1 基本原理

遗传算法(Genetic Algorithm)是一种模拟自然界遗传机制和生物进化论而形成的一种最优搜索算法。利用GA算法优化BP神经网络，是将BP神经网络中输入层到隐含层以及隐含层到输出层的初始权重和阈值进行编码串联群体中，通过遗传算法中的选择、交叉和变异操作对个体进行筛选，根据适应度函数计算出的适应度值，使优秀的个体被保留，适应度差的个体被淘汰[15]。

利用遗传算法优化BP神经网络的基本思想，要改变BP算法对梯度信息过度依赖的缺点，转而利用遗传算法全局搜索的特点，寻找最优BP神经网络连接权初值和阈值[16]。再利用BP算法对神经网络各层的权值和阈值进行迭代，从而得到优化后的神经网络预测模型。

1.2 算法步骤

GA-BP神经网络算法步骤如下[17]：

1)编码及种群初始化：将BP神经网络各层的连接权值以及阈值进行实数编码，构建成种群中的个体。这些个体实际上是由这些权值、阈值编码之后构成的数组。

2)种群进化：将遗传神经网络的预测值与期望值的误差绝对值做为个体的适应度。进化若干次，适应度值越小表示个体越优秀。

3)选择操作：本文采用轮盘赌法，基于适应度比例的选择策略，第i个个体被选择概率pi为

fi=k/Fi.

(1)

(2)

式中:Fi为个体i的适应度值，k为系数，N为种群个体数目。

4)交叉操作：由于个体采用实数编码，所以交叉操作的方法采用实数交叉法，第k个染色体ak和第l个染色体al在j位的交叉操作方法：

(3)

式中:b是[0,1]之间的随机数。

(4)

2 Adaboost遗传神经网络算法

2.1 基本思路

遗传算法能在一定程度上提升BP神经网络的基坑变形预测精度，但对于一些因样本质量问题，如样本数量少、数据分布不均等，预测精度可能降低。自适应增强(Adaboost)算法是一种有效的迭代增强算法，理论上它可以提高任何一种弱预测器的精度[18-19]。为了提高GA-BP神经网络的基坑变形预测精度，将GA-BP方法作为一种优化后的弱预测器，利用自适应增强算法调整参与训练数据的分布比重，以提高预测模型的抗差性，达到提高遗传神经网络预测精度的目的[20]。

2.2 算法步骤

自适应增强GA-BP算法的步骤如下：

1)选择样本数据{x1，x2，x3，…，xm}，并始化样本权重ωt(i)=1/m，i=1，2，3，…，m。

2)构建弱预测器，训练到第t个预测器时，利用GA-BP弱预测器构建起训练样本g与期望目标y之间的非线性关系，预测值与期望值之间的误差et：

(5)

并计算下一个弱预测器分布权值ωt+1。若误差et的绝对值大于限定阈值0.5，则需要调整分布权值。

(6)

3)计算预测权重，根据预测序列的误差和et计算序列的权重at，权重计算式为

(7)

4)预测权重归一化，调整式为

(8)

其中，Bt为归一化因子，在权重比例不变的情况下为1。

5)强预测函数。训练T轮得到T组弱预测函数f(gt,at)，由T组弱分类函数组合得到了强预测函数h为

(9)

则强预测函数预测结果y为

y(x)=ath(x).

(10)

自适应增强遗传神经网络预测模型的算法步骤如图1所示。

图1 Adaboost算法优化GA-BP神经网络流程图

Adaboost算法通过对GA-BP网络每次训练后的样本，进行权重再分配。对于训练误差小于设定阈值的样本，算法会减少该样本再次参与训练时的比例。对于训练误差大于阈值的样本，则会增加其在下次训练中的比例。最后算法会对训练的若干组弱预测器进行整合，并储存作为一个新的强预测器。最后利用得到的强预测器进行仿真实验并输出预测结果。

3 对比实验

3.1 实验数据

本文选择某小区2号楼基坑监测数据进行仿真实验。基坑开挖深度为8 m，地基等级为二级地基。按照规范要求，在基坑周围边缘顶部共布设了3个基准点和6个监测点。监测工作从2014年4月22日开始，至2015年4月19日外业观测全部结束，历时12个月。采用二等水准测量规范进行基坑沉降位移监测。观测次数50次，监测时间间隔由基坑沉降速率决定。

影响基坑沉降的外界因素众多，并且各种外界因素之间也可能相互作用[21]。难以确认各种外因对基坑沉降量的影响权重，所以本文仅考虑各期累积沉降值之间所隐含的非线性关系，构建起自适应增强遗传神经网络预测模型。

3.2 实验与结果

本文算法均在Matlab 2014a平台上编译实现。训练数据每一组都采用连续5期数据作为输入样本，将接下来1期数据作为神经网络训练的目标期望值，50期数据可以分成45组。由于沉降后期变化趋于平缓，本文选择对沉降中后期数据进行仿真预测。利用前30组进行Adaboost GA-BP预测模型的训练，并对后5期数据进行预测。将预测值与实测值进行对比，对优化后的遗传神经网络预测精度进行分析。选取平均绝对百分误差(MAPE)、误差绝对值均值(MAE)和误差均方差(MSE)作为评定预测精度的指标。平均绝对误差和误差绝对值均值由于误差被绝对值化，不会出现正负相抵消的情况，因而能更好地反映预测值误差的实际情况。误差均方差则能很好的反映36～40期预测值的精确度。

本文选择BP、Adaboost-BP、GA-BP预测模型与本文算法进行对比。4种BP神经网络的最大迭代次数均为1 000次，学习率均为0.1，学习目标设置为0.001。GA-BP和Adaboot GA-BP算法的进化次数均为80次，种群规模设置为6，交叉概率选择为0.3，变异率设置为0.2，弱预测器的数量为10。Adaboost-BP和Adaboot GA-BP算法的误差阈值设置为0.5。

图2反映了50期沉降监测数据整体的一个变化趋势。从图上可以看出前10期沉降变化剧烈，第11～30期的沉降速率趋于平缓，第31～40期沉降速率突然加快，从第41期开始，沉降趋于稳定，累计沉降量变化值趋近于零。此外神经网络模型的预测精度与训练样本数量相关，训练越充分，预测模型的精度越高。因此本文选择利用前87.5%的监测数据进行训练构建神经网络预测模型，对沉降中后期第36～40期累计沉降数据进行预测，以验证模型的预测精度。

图2 50期监测数据变化过程

表1记录了4种预测算法对于36～40期累积沉降量的预测值，其中负号表示沉降的方向竖直向下。图3为4种算法的预测误差对比图，预测误差以毫米为单位，从图上可以更直观地看出，与其他3种算法相比，Adaboost GA-BP算法的预测误差更接近于0值。从表2可以看出，后3种算法对于BP预测算法均有改进，其中精度最高的为本文提出的改进算法。Adaboost GA-BP算法后5期预测值的平均绝对百分误差为0.68%，误差绝对值均值为0.29，误差均方差为0.49。对比BP算法和Adaboost-BP算法的预测结果，可知Adaboost算法能够有效提高神经网络预测模型的预测精度。对比GA-BP和Adaboost GA-BP算法的预测结果可知，Adaboost GA-BP算法较GA-BP算法在MAPE、MAE、MSE 3项精度指标上分别提高了80.57%、81.04%、70.83%。

为了验证Adaboost GA-BP算法的有效性和鲁棒性，以及避免预测结果的偶然性。本文选取了同一测区其他3个监测点的数据进行仿真预测。从表3的精度指标可以看出，B01、B03和B04第36～40期预测数据的均方根误差分别为0.48、0.22、0.34，平均误差绝对值分别为0.44、0.19、0.30，平均绝对百分误差分别为1.03%、0.46%、0.72%。说明本文算法对不同监测点累计沉降量的预测效果优异，且算法的预测稳定度高。

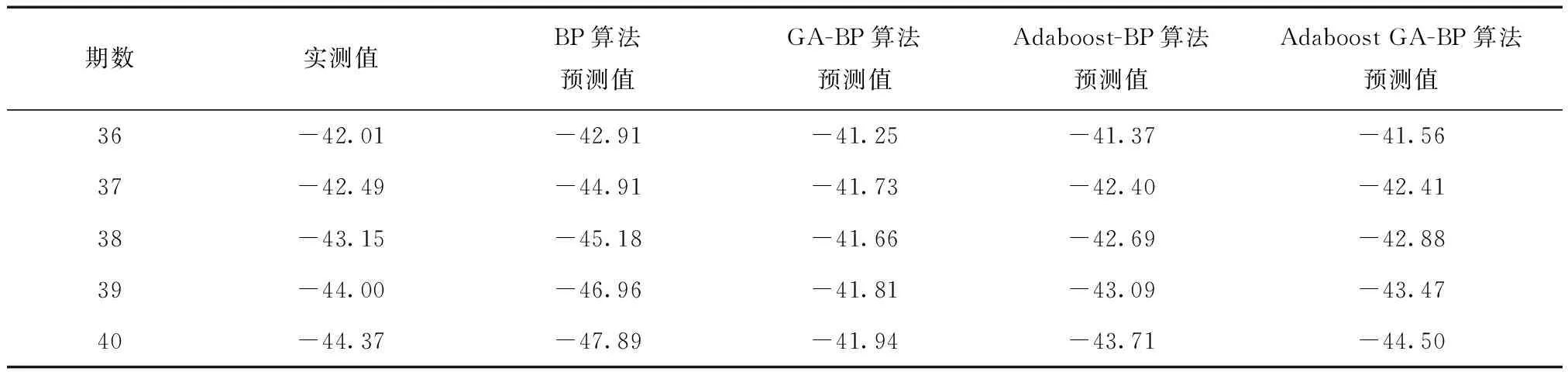
表1 各预测模型预测结果对比 mm

表2 各预测模型预测精度对比

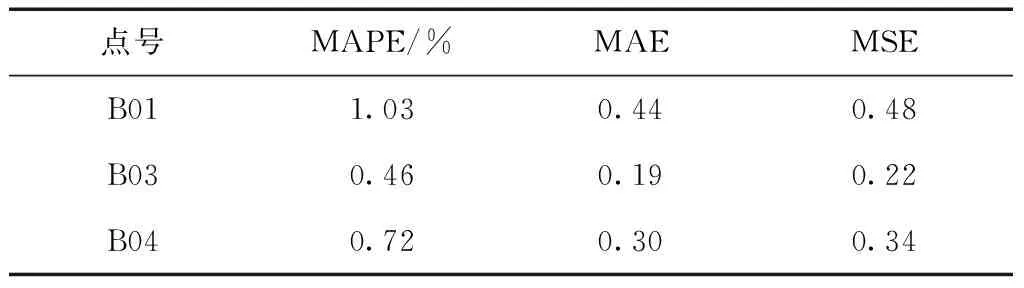
表3 Adaboost GA-BP算法对不同监测点数据的预测精度

图3 各算法预测误差大小对比

4 结论

利用GA算法优化过的BP预测模型，能够有效克服BP预测模型容易陷入局部最优的缺点。但是由于监测数据在时间上的分布不均，或者测量数据中包含一定粗差而导致GA-BP累积沉降预测模型精度受到影响的问题仍然存在。因此本文引入了自适应增强算法改进GA-BP神经网络预测模型，并应用于基坑沉降预测当中。实验结果证明Adaboost优化过的GA-BP预测模型的沉降预测值在误差绝对值均值、平均绝对百分误差以及误差均方差上都明显优于GA-BP模型的预测结果。说明了自适应增强遗传神经网络预测模型结合了Adaboost算法和GA算法的优点，提高了模型的预测精度。利用实际工程数据进行实验，实验结果证明了自适应增强算法优化过的遗传神经网络能够很好地应用于基坑沉降预测，且预测模型具有很好的鲁棒性，预测精度能够满足基坑监测的要求。

[1] 岳建平, 方露, 黎昵. 变形监测理论与技术研究进展[J]. 测绘通报, 2007(7):4-7.

[2] 徐爱功, 李娜, 张涛. 时间序列分析在地铁沉降观测中的应用[J]. 测绘科学, 2013, 38(5):57-60.

[3] LU F, LI J. Application of Kalman Filter Method Based on Model Optimization Method in the Dam Deformation Forecast[C]// Asia-Pacific Power and Energy Engineering Conference. IEEE Computer Society, 2011:1-4.

[4] 黄定川, 谢世成. 一种基于 BP 神经网络的尾矿坝沉降预报方法[J]. 测绘工程, 2016, 25(8):53-56.

[5] 张文博, 郭云开. 基于BP神经网络的建筑物沉降预测模型研究[J]. 测绘工程, 2013, 22(2):52-56.

[6] 马丽霞, 王凤艳, 陈剑平. 基于人工神经网络的大坝变形分析与预报——以西津大坝27#点的变形监测为例[J]. 吉林大学学报(地球科学版), 2009,39(3):487-491.

[7] 刘贺, 张弘强, 刘斌. 基于粒子群优化神经网络算法的深基坑变形预测方法[J]. 吉林大学学报(地球科学版), 2014, 44(5):1609-1614.

[8] 史雨川. 基于AFSA—BP神经网络的基坑变形预测模型研究[J]. 计算机与数字工程, 2013, 41(12):1894-1897.

[9] 岳荣花. 小波神经网络在沉降预测中的应用研究[D]. 南京：河海大学, 2007.

[10] 李超. 小波神经网络在大坝变形预测中的应用研究[D]. 西安：长安大学, 2012.

[11] 薛鹏松, 冯民权, 邢肖鹏. 基于马尔科夫链改进灰色神经网络的水质预测模型[J]. 武汉大学学报(工学版), 2012, 45(3):319-324.

[12] 张林,刘先珊, 阴和俊. 基于模拟退火的Gauss-Newton算法神经网络在短期负荷预测中的应用[J]. 武汉大学学报(工学版), 2005, 38(4):28-33.

[13] 李金锋. 遗传BP神经网络在地铁工程沉降预测中的应用[D]. 北京：中国地质大学, 2006.

[14] 张正禄. 工程的变形监测分析与预报[M]. 北京：测绘出版社, 2007.

[15] 刘勇健, 李彰明, 张建龙,等. 基于遗传-神经网络的深基坑变形实时预报方法研究[J]. 岩石力学与工程学报, 2004, 23(6):1010-1014.