过滤白噪声地震动模型的CQC振型相关系数计算
2018-03-20周晓青
王 刚,周晓青
深圳大学土木工程学院,广东深圳 518060
目前,振型分解反应谱法广泛用于抗震设计,利用抗震设计规范中给出的设计反应谱,可方便地计算各振型地震反应的最大值,并利用平方和开方(square root of the sum of the squares,SRSS)或完全二次型组合(complete quadratic combination,CQC)进行振型组合.由于CQC法精度高,且简单实用,因此得到广泛应用.现在常用的CQC振型组合系数公式是由KIUREGHIAN等[1-7]提出的,该公式基于地震动为零均值平稳白噪声的假设,利用随机振动理论推导而来.周锡元等[8-9]将其推广到复模态分解反应谱法,给出了复振型的完全二次型组合(complex complete quadratic combination, CCQC)组合系数计算公式.也是基于地震动为零均值平稳白噪声的假设推导出来的,即假设地震动输入带宽足够大,可覆盖对整体贡献显著的那些振型,当这个假设不能满足时,现行的CQC组合方法将无法达到足够的精度.因此,更精确地考虑地震动模型有助于改善CQC组合[1-2,4].
地震动模型常见的有过滤白噪声模型,如Kanai/Tajimi模型[10-11],以及在此基础上改进的各种功率谱模型[12-15].有关地震动模型,文献[16]做了详尽综述.在文献[4]中,KIUREGHIAN等将CQC组合方法进一步扩展到输入为窄带白噪声的情况,此外,还考虑了被截断高阶模态的准静态贡献,以及输入截止频率的影响等因素.CQC振型相关系数计算基于以下假设:地震动为零均值平稳随机过程,结构的最大反应正比于相应的根方差,且不同振型之间,振型最大反应与根方差的比例常数相同.考虑过滤白噪声地震动模型时,CQC组合的振型相关系数推导常常需要在频域内进行积分,其结果变得复杂冗长[1],严重影响了实用性能.
本研究给出了地震动为过滤白噪声的情况下,CQC组合振型相关系数的一种新算法,这种方法避开了复杂冗长的频域积分,计算简洁实用,结果为精确解.
1 CQC组合系数计算方法
考虑地震作用下的结构振动方程
(1)

(2)
其中,γi=(φTiL)/(φTiMφi), 为振型参与系数.

其中,振型相关系数ρij的推导基于以下假设:地震动为零均值平稳随机过程,结构的最大反应正比于相应的根方差,且不同振型之间,振型最大反应与根方差的比例常数相同.从而,
(3)

其中,
记
(4)
则式(3)还可以写成
(5)

(6)
这里,r=ωi/ωj为频率比.

考虑1输入2输出的线性系统
(7)
其状态空间方程可以写成
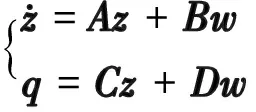
(8)
其中, (A,B,C,D)为相应的系数矩阵,由于Hi(ω)和Hj(ω)是严格真有理函数,所以D=0, 其余系数矩阵详见后面讨论;q是输出向量,q=[qiqj]T;w是输入,当w是零均值白噪声,且E(w2)=1时,输出q的协方差矩阵[17]可写成
E[qqT]=CPCT
(9)
其中,P是如下Lyapunov方程的解
AP+PAT+BBT=0
(10)
求解Lyapunov方程(10)已有成熟的算法[18-19],且在本文情况中方程(10)阶数很低,计算量很小,容易求得P, 进而由式(9)和式(3)求出振型相关系数.理论上,该方法与计算积分(4)及式(5)方法等价,是精确解[17].
令(Ai,Bi,Ci,0)、 (Aj,Bj,Cj,0)和(Ag,Bg,Cg,Dg)分别为Hi(ω),Hj(ω)和G(ω)的状态空间系数矩阵,则状态方程(8)的系数矩阵分别为
(11)
以常见的Kanai/Tajimi模型为例,
(12)
其中,j表示虚部,相应的状态方程系数矩阵为
(13)
Hi(ω),Hj(ω)的状态方程系数矩阵为
Cm=[1 0],m分别取i和j.
(14)
当地震动模型为白噪声时,G(ω)=1, 式(11)退化为只保留前两行两列分块矩阵,按本算法计算结果与式(6)完全相同.
当地震动模型为其他过滤白噪声类型时,只是滤波器G(ω)的具体形式,以及对应的状态方程系数矩阵(Ag,Bg,Cg,Dg)有所不同,振型相关系数均可按本算法进行计算.
综上,利用式(11)构造矩阵A、B、C进而求解Lyapunov方程(10),并利用式(9)和式(3)求出振型相关系数.
2 算 例
Kanai/Tajimi模型取ωg=10 rad/s,ξg=0.65. 其功率谱密度函数如图1,给出的El Centro地震波的功率谱密度作为参考.
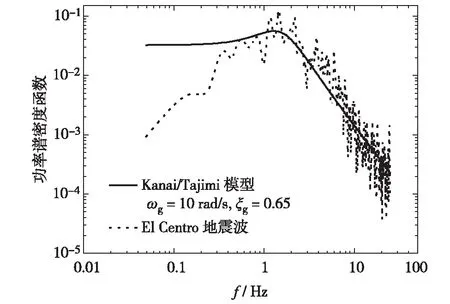
图1 Kanai/Tajimi模型的功率谱密度函数Fig.1 Power spectrum density function of Kanai/Tajimi model
由于矩阵A只有6×6阶,Lyapunov方程(10)的求解耗时非常少,在实际结构分析中其计算量完全可忽略不计.
图2是在振型阻尼比ξi=ξj=0.05,ωj=5、 10、 20、 50、 100 rad/s,假设地震动为Kanai/Tajimi模型时,得到的振型相关系数ρij与r的关系曲线,作为对比,图2中也给出了白噪声模型下即式(6)的结果.
从图2可知,与白噪声模型相比,假设地震动为Kanai/Tajimi模型时,在频率比远离1的情形,振型相关系数不一定趋近于0;高阶振型对整体的贡献较白噪声假设的结果显著.这个结果与文献[2]一致.

图2 振型相关系数与频率比的关系曲线Fig.2 Modal correlation coefficient versus frequency ratio
结 语
本研究提出通过求解Lyapunov方程,得到CQC振型组合系数的方法,这种方法避开了在频域里对有理分式的冗长积分结果,计算量小,算法成熟可靠,可用于解决常见的过滤白噪声地震动模型问题.
/
[1] KIUREGHIAN D A. A response spectrum method for random vibration: UCB/EERC-85/15[R]. EERC, Berkeley: University of California, 1980.
[2] KIUREGHIAN A D. A response spectrum method for random vibration analysis of MDF systems[J]. Earthquake Engineering and Structural Dynamics, 1981, 9: 419-435.
[3] WILSON E L, BAYO E P. A replacement for the SRSS method in seismic analysis[J]. Earthquake Engineering and Structural Dynamics, 1981, 9(2): 187-194.
[4] KIUREGHIAN D A, NAKAMURA Y. CQC modal combination rule for high-frequency modes[J]. Earthquake Engineering and Structural Dynamics, 1993, 22(11): 943-956.
[5] POZZI M, KIUREGHIAN D A. Response spectrum analysis for floor acceleration[J]. Earthquake Engineering and Structural Dynamics, 2015, 44(12): 2111-2127.
[6] MENUN C, REYES J C, CHOPRA A K. Errors caused by peak factor assumptions in response-spectrum-based analyses[J]. Earthquake Engineering and Structural Dynamics, 2015, 44(12): 1729-1746.
[7] NAKAMURA Y. Application of CQC method to seismic response control with viscoelastic dampers. in: gardoni p.(eds) risk and reliability analysis: theory and applications[M]. Springer Series in Reliability Engineering. Cham: Springer, 2017.
[8] 周锡元,马东辉,俞瑞芳.工程结构中的阻尼与复振型地震响应的完全平方组合[J].土木工程学报,2005, 38(1):31-39.
ZHOU Xiyuan, MA Donghui, YU Ruifang. Damping in structures and complete quadratic combination (CCQC) of complex mode seismic responses[J]. China Civil Engineering Journal, 2005, 38(1):31-39.(in Chinese)
[9] 王 刚,王 远,周文松.考虑一阶系统参与组合的复模态分解反应谱法[J].地震工程与工程振动,2013, 33(4):89-94.
WANG Gang, WANG Yuan, ZHOU Wensong. Complex modal superposition response spectrum method with first order system entering combination[J]. Earthquake Engineering and Engineering Vibration, 2013, 33(4): 89-94.(in Chinese)
[10] KANAI K. Semi-empirical formula for the seismic characteristics of the ground[J]. Bulletin of the Earthquake Research Institute, 1957, 35(2): 309-325.
[11] TAJIMI H. A statistical method of determining the maximum response of a building structure during an earthquake[C]// Proceedings of the Second World Conference on Earthquake Engineering, Tokyo and Kyoto, Japan: Science Council of Japan, 1960, 2:781-798.
[12] CLOUGH R W, PENZIEN J. Dynamics of structures[M]. New York: McGraw-Hill,1993.
[13] 欧进萍, 牛荻涛, 杜修力.设计用随机地震动的模型及其参数确定[J].地震工程与工程震动, 1991,11(3):45-54.
OU Jinping, NIU Ditao, DU Xiuli. Random earthquake ground motion and its parameter determination used in aseismic design[J]. Earthquake Engineering and Engineering Vibration, 1991,11(3): 45- 54.(in Chinese)
[14] 洪 峰, 江近仁, 李玉亭. 地震地面运动的功率谱模型及其参数的确定[J].地震工程与工程震动, 1994, 14(2):48-54.
HONG Feng, JIANG Jinren, LI Yuting. Power spectral models of earthquake motions and evaluation of its parameters[J]. Earthquake Engineering and Engineering Vibration,1994,14(2): 48-54.(in Chinese)
[15] 杜修力, 陈厚群. 地震动随机模拟及其参数确定方法[J]. 地震工程与工程振动, 1994, 14(4): 1-5.
DU Xiuli, CHEN Houqun. Random simulation and its parameter determination method of earthquake ground motion[J]. Earthquake Engineering and Engineering Vibration, 1994,14(4): 1-5.(in Chinese)
[16] 李英民,刘立平,赖 明. 工程地震动随机功率谱模型的分析与改进[J]. 工程力学,2008,25(3):43-48,57.
LI Yingmin, LIU Liping, LAI Ming. Analysis and improvement of power random spectra of strong ground motions for engineering purpose[J]. Engineering Mechanics, 2008,25(3):43-48, 57.(in Chinese)
[17] 韩崇昭. 随机系统概论——分析估计与控制[M].北京:清华大学出版社,2014.
HAN Chongzhao. Introduction to stochastic systems: analysis, estimation and control[M]. Beijing: Tsinghua University Press, 2014.(in Chinese)
[18] BARTELS R H, STEWART G W. Solution of the matrix equationAX+XB=C[J]. Communications of the ACM, 1972,15(9):820-826.
[19] GOLUB G H, NASH S, VAN LOAN C F. A Hessenberg-Schur method for the problemAX+XB=C[J]. IEEE Transactions on Automatic Control, 1979, 24(6): 909-913.
