考虑瓶颈路段饱和度的交通需求控制评价

凃 强，程 琳，马 捷，纪 魁

1)东南大学交通学院，江苏南京 210096；2)江苏省城市规划设计研究院，江苏南京 210013

城市规划已从增量规划向存量规划转变，城市交通发展不能仅靠交通供给方面的政策，同时需要对交通源头进行管理，抑制交通的产生，必须对交通需求进行调控，从交通需求和交通供给两方面解决城市交通拥堵问题[1]．交通需求管理已经成为大城市解决城市交通问题的主要方法之一，对交通需求控制方案进行评价具有十分重要的意义．

交通需求管理作为宏观调控政策，通常需要建立一个指标体系，收集大量定量和定性的数据进行综合评价．但交通需求控制策略涉及的范围广，相应评价指标体系较为复杂，导致基础数据收集困难，同时评价指标体系主要是对既有效果进行评价，未能很好预测交通需求控制方案所能达到的效果[2-3]．

本研究从一个简单的交通悖论现象着手，分析将瓶颈路段饱和度作为评价指标的必要性．以提高路网总体运行效率和缓解道路拥堵效果作为评价依据，分别从整体和局部的角度出发，选取路网总费用，路网平均饱和度和瓶颈路段饱和度3个指标对交通需求管理控制效果进行评价；提出的评价指标易于理解，运算快捷有效．

1 交通悖论

在交通网络中增加路段的数量，不但没有缓解网络拥挤状况，反而使路网总出行费用增加，这就是交通网络中的Braess悖论，其本质在于用户均衡条件下各出行者的不协调性，仅考虑自身的最短路径，不考虑自身选择对其他出行者的影响，即使在路网中新增道路，路网总费用仍有可能增加[4-7]．

传统的交通网络悖论是考虑新增路段对路网总出行费用的影响，在用户均衡条件下，存在另一种交通悖论现象：交通管理者通过交通需求管理，使起讫点(origin-destination，OD)交通量减少，而道路中某些路段的流量增加，变得更加拥堵，如图1．

图1 算例网络Fig.1 Example network

由图1可见，该网络共包含5条路段，其费用函数分别为t1=50+x1、t2=50+x2、t3=10x3、t4=10x4和t5=10+x5， 其中，xi为路段流量，i=1,2,3,4,5．

当OD=7时，对该网络进行用户均衡交通分配，得到路段流量x1=x2=2.85，x3=x4=4.15，x5=1.31．

当OD=6时，对该网络进行用户均衡交通分配，得到路段流量x1=x2=x5=2，x3=x4=4．

由计算结果可知，当OD交通量减小时，虽然路段1至路段4的流量都减小了，但路段5的流量反而由1.31增至2.00，其拥堵反而更加严重．

由于该网络较小，设OD交通量为q， 数值计算得到路径和路段流量的表达式，如表1．可见，路段5的流量等于路径2的流量，均是OD交通量q的单调递减函数．由于对称性，路径1和路径3的流量相等，此外还可以得到路径2流量是路径1和3流量的单调递减函数．上述现象可以理解为：当OD交通量q减少，为达到用户均衡，路径1和路径3流量减少的同时，部分流量会转移到路径2上，造成路径2流量增加，从而路段5的流量也增加．

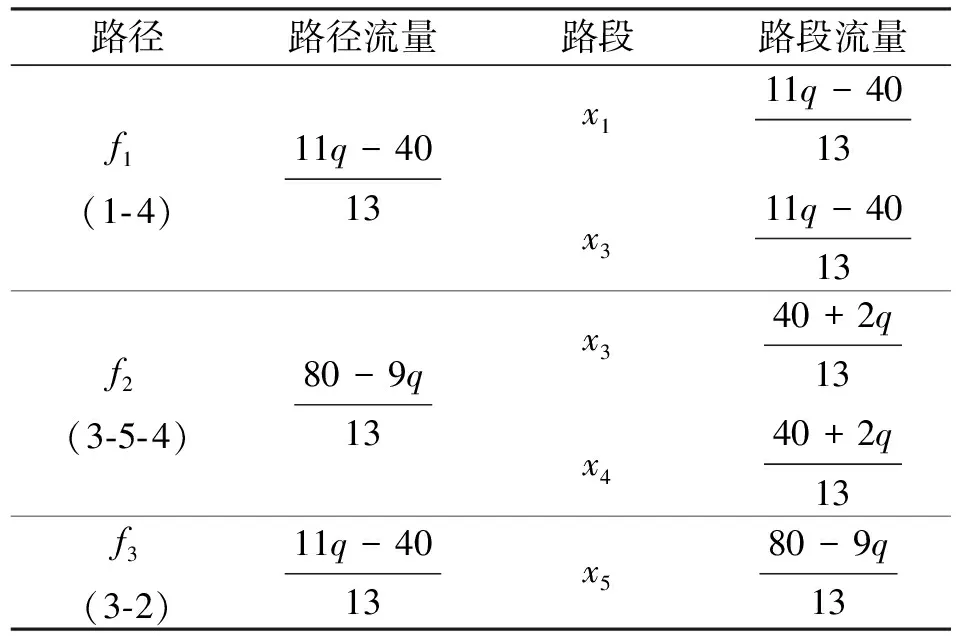
表1 算例网络中路径和路段流量表达式Table 1 The expression of path and link flow in example network

在此种交通悖论情形下，交通管理者即使通过交通需求管理减少了OD交通量，也有可能不能缓解瓶颈路段的拥堵状况．

2 评价指标

交通需求控制的目的是为了缓解交通拥堵，提高路网的运行效率．因此，考虑交通需求控制对路网运行效率的影响，进而评价交通需求控制方案的实施效果．常用的交通路网运行效率评价指标有：路网总费用和路网平均饱和度[7-9]，通过之前对交通悖论的分析，提出将瓶颈路段饱和度作为评价指标，3项指标的具体描述如下．

2.1 路网总费用

路网总费用是从系统总体出发，考虑所有路段的流量及其费用的乘积，反映整个路网所有出行者费用的总和，可表示

(1)

其中，xa为路段a的流量；ta为路段a的费用．

2.2 路网平均饱和度

平均饱和度是指路网中所有路段饱和度的平均值，反映路网中所有路段拥堵的平均水平，但不能反映路段饱和度的拥堵分布和方差．可表示

(2)

其中，ca为路段a的通行能力；n为路网中路段数量．

2.3 瓶颈路段饱和度

瓶颈路段饱和度是指路网中最拥堵路段的饱和度，反映路网中路段的拥堵上限，但不能很好反映路网的总体情况和平均水平．在实际情况中，交通管理者希望通过需求管理控制，改善瓶颈路段的拥堵情况，因此，该项指标具有重要现实意义．其数学表达式为

V(x)=max(xa/ca)

(3)

3 数学模型和求解算法

前述3项评价指标中，可以任选1个或者多个指标作为目标函数，求解最优的交通需求控制方案．选取多个指标作为目标函数时，需要对各指标进行标准化处理，并加以一定权重．各指标的权重可以根据管理者对各项指标的重视程度进行设定，指标的标准化可采用

A′(x)=A(x)/A*(x)

(4)

其中，A′(x)为标准化后的评价指标取值；A(x)为方案实施后评价指标取值；A*(x)为未实施方案的原始评价指标取值．当A(x)>A*(x)时，A′(x)可能大于1，但这对评价结果并没有影响．

为计算评价指标，除了ca和n已知外，还要求得xa和ta， 在交通需求控制方案已知的情况下，认为OD交通量q为已知，只需通过交通分配即可求得xa．采用标准的BPR函数，ta可写成xa的函数，

ta(xa)=t0[1+0.15(xa/ca)4]

(5)

其中，t0为路段a的自由流出行时间．

通过选取评价指标加权最小作为上层数学模型，用户均衡交通分配模型作为下层数学模型，该问题转化为如下双层数学规划模型．

1)上层模型

minF(x)=αC′(x)+βM′(x)+γV′(x)

(6)

s.t.q∈Q

(7)

2)下层模型

(8)

(9)

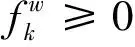
(10)

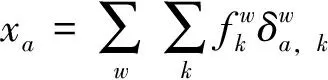
(11)

一般情况下，双层规划模型的求解比较困难，然而在实际工程中，交通需求控制方案数量有限，可以采取对方案集Q中方案进行枚举计算，筛选出上层目标函数最优的方案作为最终方案，因此，只需要对下层交通分配模型进行求解．

求解下层用户均衡交通分配模型可采用经典的Frank-Wolfe方法，但为了得到一组路径解便于后文分析，此处采用一种基于有效路径的相继平均算法，其具体步骤如下．

步骤3更新路径和路段流量．

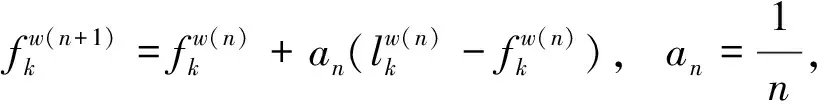
步骤4收敛检验．

4 案例分析

Nguyen-Dupuis(ND)网络由NGUYEN和DUPUIS在1984年提出，并在交通网络分析中得到广泛引用[10]，其包含4个OD对，13个节点和19条路段，具体参数取值如图2．通过用户均衡模型进行交通分配，得到各个路段流量xa， 从而计算得到其饱和度va， 如图3．

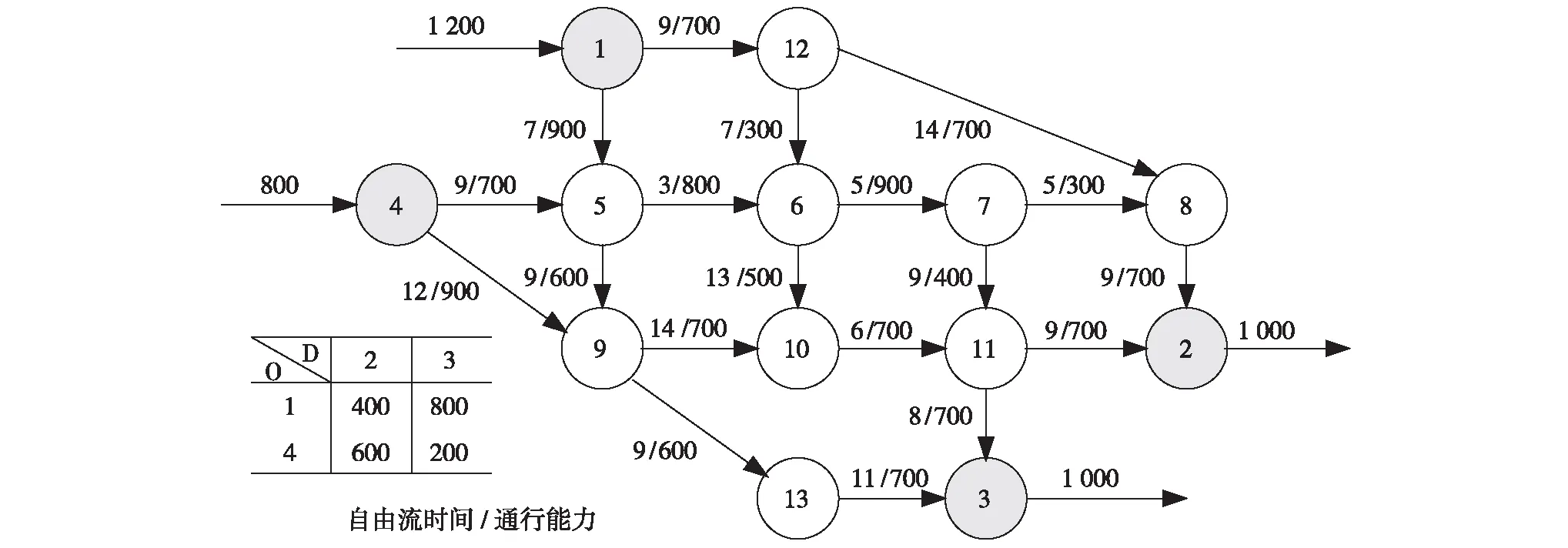
图2 ND网络基本参数Fig.2 Basic parameters of ND network

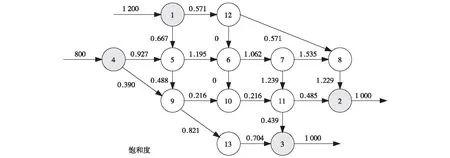
图3 ND网络路段饱和度Fig.3 Link saturation of ND network

由图3可见，路段7至路段8的饱和度达到1.535，为路网中的瓶颈路段；路网总费用为76 072，平均饱和度为0.671．为改善路网的运行效率，减少路段7至路段8的拥堵状况，交通管理部门采取交通需求管理措施，以减少OD交通出行需求．

表2 交通需求控制方案

以下从路网总费用、路网平均饱和度和瓶颈路段饱和度3个指标对该15种方案进行分析评价．在评价之前，采用式(4)对各项指标取值进行标准化处理，具体分析评价如下．

4.1 路网总费用

图4 标准化路网总费用指标与的关系Fig.4 The relationship between normalized index of road-network total cost and

4.2 路网平均饱和度

图5 标准化路网平均饱和度指标与的关系Fig.5 The relationship between normalized index of mean road-network saturation and

4.3 瓶颈路段饱和度

图6 标准化瓶颈路段饱和度指标与的关系Fig.6 The relationship between normalized index of bottleneck links saturation and

综上分析可知，各交通需求控制方案的路网总费用和路网平均饱和度改善效果差异在2.25%以内，并不显著，若仅比较这两项评价指标，可能难以判断哪种方案更优．而各方案对于改善瓶颈路段饱和度却呈现出较大差异，最大时达7.65%，因此，考虑瓶颈路段饱和度的交通需求控制评价很有必要．

除此分析外，还有两点值得思考：① 如果一直增加OD对1-2交通量，那么路段7-8的饱和度是否会一直减小？②是什么原因造成OD对1-2交通量的增加，而路段7-8的拥堵程度反而减小？

图7 路段7-8和瓶颈路段饱和度与OD对1-2交通量的关系Fig.7 The relationship between the saturation of link 7-8and bottleneck link and traffic demand of OD 1-2

为回答问题①，考虑仅控制OD对1-2的交通量由400～2 000进行变化(公差取20)，分析路段7-8的饱和度变化．图7为路段7-8和瓶颈路段饱和度与OD对1-2交通量的关系. 可见，当OD对1-2交通量的增加到540时，路段7-8已经不再是瓶颈路段(此后瓶颈路段变为路段8-2)，随着OD对1-2的交通量持续增加，路段7-8的饱和度会继续下降，直到OD对1-2的交通量达到1 140，此后路段7-8的饱和度会开始增加．

由于ND网络规模不大，可以通过基于有效路径的算法，求得均衡条件下的一组路径解，从而分析路径流量的转移状态以回答问题②．需要分析的路径流量包括连接OD对1-2的共8条路径的流量，和连接路段7-8的3条路径(其中，2条路径在连接OD对1-2的8条路径当中，另外一条路径连接的OD对为4-2)的流量．这9条路径如表3．

表3 需要分析的路径

在运算过程中发现，路径5、6、7和8的流量为0或者很小，因此，仅需要分析路径1、2、3、4和9共5条路径的流量变化．根据路段7-8的流量变化状态，分成两个部分分析问题②．

4.3.1 路段7-8的流量(饱和度)减小阶段.

图8为路径流量与OD对1-2交通量的关系. 可见，随着OD对1-2交通量的增加，连接OD对1-2的路径1、2、3和4的流量都开始增加．由路径和路段关系可知，路段5-6和6-7的流量也开始增加，导致其路段费用增加，由于路径9经过路段5-6和6-7，此时路径9的费用增加，导致路径9的流量开始向连接OD对4-2的其他路径转移，因此，路径9的流量开始持续下降．而路段7-8的流量为路径2和路径9的流量之和，由于路径9减少的流量大于路径2增加的流量，因此，随OD对1-2交通量的增加，路段7-8的流量(饱和度)一开始是减少的．

4.3.2 路段7-8的流量(饱和度)增大阶段.

随着OD对1-2的交通量持续增加，连接OD对1-2的路径1、3和4的流量持续上升，而路径2的流量变化开始发生波动，呈先降后升趋势．路径9的流量也由之前的持续下降变为先升后降的趋势，但路径2和路径9的流量之和是呈上升趋势，因此路段7-8的流量(饱和度)开始持续上升．

图8 路径流量与OD对1-2交通量的关系Fig.8 The relationship between paths flow and traffic demand of OD 1-2

结 语

本研究分析一种交通悖论现象：OD交通量的减少可能会导致路段交通流量的增加，并从路径流量转移的角度分析其内在原因．分析路网总费用、路网平均饱和度和瓶颈路段饱和度3项指标，提出一种考虑交通网络瓶颈路段饱和度的交通需求控制评价方法．采用数值实验的方法进行相应的案例分析，进一步说明考虑瓶颈路段饱和度作为评价指标的必要性，同时论证评价方法的有效性．研究结果表明，交通网络是一个复杂的系统，不合理的交通管理策略可能会产生交通悖论，因此，交通管理者在进行交通需求管理时，需要系统全面地对交通管理控制方案进行综合评价，从而制定科学合理的交通需求管理控制方案，否则所实施的交通管理措施可能会造成交通拥堵路段更加拥堵的情况，结果适得其反．

/

[1] 王丰元，陈萌三，宋年秀.交通需求管理及其在中国的应用[J].交通运输工程学报, 2002, 2(2): 83-87.

WANG Fengyuan, CHEN Mengsan, SONG Nianxiu. Application of travel demand management in China [J]. Journal of Traffic and Transportation Engineering, 2002, 2(2):83-87.(in Chinese)

[2] 杨夫军.交通需求管理评价指标体系研究[D]. 南京：东南大学，2006.

YANG Fujun. Study on the evaluated indices system of the traffic demand management[D]. Nanjing: Southeast University,2006.(in Chinese)

[3] 何建伟，曾珍香，李志恒.北京市交通需求管理政策效用分析[J].交通运输系统工程与信息，2009，9(6)：114-119.

HE Jianwei, ZENG Zhenxiang, LI Zhiheng. An analysis on effectiveness of transportation demand management in Beijing[J].Journal of Transportation Systems Enginee-ring and Information Technology, 2009, 9(6):114-119.(in Chinese)

[4] BRAESS D. Über ein Paradoxon aus der Verkehrsplanung[J]. Mathematical Methods of Operations Research, 1968, 12(1): 258-268.

[5] DAFERMOS S, NAGURNEY A. On some traffic equilibrium theory paradoxes[J]. Transportation Research Part B: Methodological, 1984, 18(2): 101-110.

[6] 赵春雪，傅白白，王天明.拥挤交通网络的Braess’悖论现象[J].交通运输系统工程与信息，2012，12(4):155-160.

ZHAO Chunxue, FU Baibai, WANG Tianming. Braess’ paradox phenomenon of congested traffic networks[J].Jouornal of Transportation Systems Engineering and Information Technology, 2012, 12(4):155-160.(in Chinese)

[7] 程 琳.城市交通网络流理论[M].南京：东南大学出版社，2010：29-31.

CHENG Lin. Urban transportation network flow theory[M]. Nanjing: Southeast University Press, 2010: 29-31.(in Chinese)

[8] MA Jie, LI Dawei, CHENG Lin, et al. Link restriction: methods of testing and avoiding braess paradox in networks considering traffic demands[J]. Journal of Transportation Engineering Part A: Systems, 2017, 144(2): 04017076.

[9] 林 杰.山地城市交通设施人性化规划设计研究[D]. 重庆：重庆交通大学，2015.

LIN Jie. Study on planning and design of the facility humanization of mountain city traffic[D]. Chongqing: Chongqing Jiaotong University,2015.(in Chinese)

[10] NGUYEN S, DUPUIS C. An efficient method for computing traffic equilibria in networks with asymmetric transportation costs [J]. Transportation Science, 1984, 18(2): 185-202.