LOCALIZED PATTERNS OF THE CUBIC-QUINTIC SWIFT-HOHENBERG EQUATIONS WITH TWO SYMMETRY-BREAKING TERMS∗†

Yancong Xu,Tianzhu Lan

(Dept.of Math.,Hangzhou Normal University,Hangzhou 310036,Zhejiang,PR China)

Zhenxue Wei‡

(School of Computer Science and Software Engineering,East China Normal University,200062,Shanghai,PR China)

1 Introduction

In recent years,there has been a lot of interest in localized patterns in some partial differential equations on the real line[4-24],including numerous physical,biological and chemical models[1,3];see also[2,11]for additional references.As we know,these localized states can bifurcate from the trivial state.At the same time,they often exhibit homoclinic snaking when they approach a spatially periodic structure[18,19],especially in some reversible and variational systems[5,7,11,21].Note that,the term snaking refers to the back-and-forth oscillations of the localized patterns within the parameter space region as localized states grow in width.As a matter of fact,the term “spatially localized pattern” refers to particular stationary solution of the partial differential equations.The addressed localized roll patterns correspond to homoclinic orbits of the associated ordinary differential equations,and the equilibrium and periodic orbit corresponds to the background state and regular periodic pattern of partial differential equations,respectively.As a specified example,we consider the general cubic-quintic Swift-Hohenberg equation

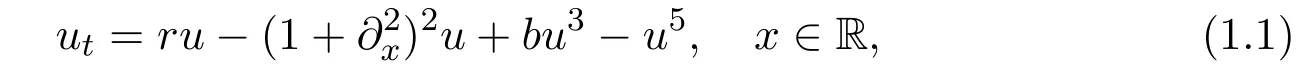
with b=2,which is invariant under the symmetry R:x→ −x,k:u→ −u.It has been studied by a number of authors[5,21].This equation has two kinds of symmetries:R:x→ −x(reversible)and k:u→ −u,the effect of k◦R is to force the drift speed to vanish.In fact,the asymmetric states are also equilibria due to the variational structure of the cubic-quintic Swift-Hohenberg equation.Note that,these asymmetric states are known to be unstable.It is possible to make the oddparity states drift by breaking the midplane reflection symmetry k of the system.

As we know,this equation has the usual snakes and ladders,and there are three kinds of patterns:a snaking branch representing even-parity solutions,that is,solutions invariant with respect to R,a snaking branch representing odd-parity solutions with respect to k◦R,and the rung states.The rung states connect the two snaking branches,arising in pitch-fork bifurcations close to the saddle-node bifurcations on the snaking branches.Moving up along the snake branch,the saddle nodes converge exponentially rapidly to a fixed values of the parameter r and do so from the same side at both boundaries of the snaking region.At the same time,the pitchfork bifurcations leading to the rung states converge exponentially rapidly to the saddle-node bifurcations.

Stationary localized patterns of(1.1)can be reduced to homoclinic orbits of the steady-state equation

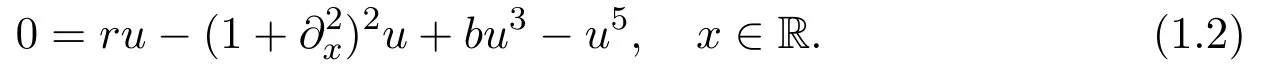
This equation can be written as the first-order ordinary differential equation

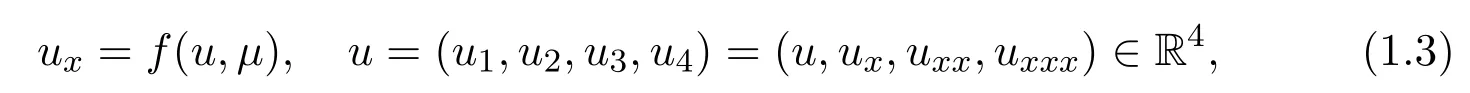
which is a reversible Hamiltonian system.

The structure of variational

where F and H0are the energy and the Hamiltonian conserved by the time-independent version of equation(1.1)written as a dynamical system in space respectively.In fact,the occurrence of branches not requiring the spatial dynamical system is conservative which means that the corresponding PDE system needn’t to be a variational system.

The quadratic-cubic Swift-Hohenberg equation with broken reversibility term was investigated analytically by Sandstede and Xu[14]and Knobloch,Vielitz and Wagenknecht[16].In those two papers,the structure of the bifurcation diagram of localized rolls was investigated for variational but non-reversible systems,also conditions were derived to guarantee the existence of snaking or isolas.It is therefore of interest to know the results of weak breaking of the reversibility or k-symmetry in an extended cubic-quintic Swift-Hohenberg equation.

In this paper,we will examine the effect of adding two dispersive terms to equation(1.1),that is,one term to break the reversibility,the other term to break k-symmetry step by step.

At first,consider the following cubic-quintic Swift-Hohenberg equation with broken reversibility term:

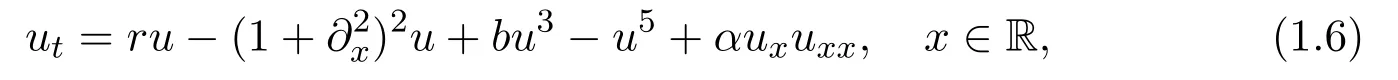
which breaks the reversible condition x→ −x and k-symmetric condition k:u→−u,but keeps the Hamiltonian nature that can guarantee the dynamics of a threedimensional level set of the Hamiltonian,that is,the four-dimensional system can be reduced to a three-dimensional system.Note that,the Maxwell point r=rMis de fined by F=H=0,where

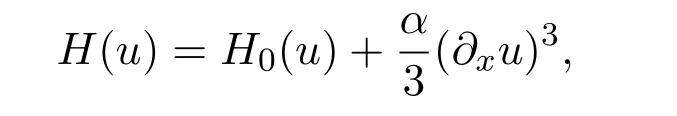
with F and H being respectively the energy and the Hamiltonian conserved by the time-independent version of equation(1.6)written as a dynamical system in space.

Meanwhile,we are also interested in the Swift-Hohenberg equation with the other kind of broken k-symmetry term

which contains a quadratic term that breaks the k-symmetry but respects the R-symmetry.However,is a non-variational term to(1.7).It has been studied numerically and analytically by Houghton and Knobloch[12],Makrides and Sandstede[15].It was observed and explained that the even solutions persist along the original snaking branches,while the odd solutions are changed into two types of asymmetric branches due to the k-symmetry-breaking term,that is,S-branch and Z-branch.The Z-branch starts and ends on the same symmetric snake branch while the S-branch connects the two symmetric branches to each other.

As the above-mentioned reasons,it is natural to ask what happens when both structures are broken step by step.Then we are also interested in investigating the following Swift-Hohenberg equation with two kinds of broken symmetry terms

which is a non-reversible and non-k-symmetric system.Especially,if we change the process of destroying the different symmetries,then we can obtain different snakes or isolas,and can find the Hamiltonian effect on snake is small when we destroy the conservative system.The dynamics and structure of localized patterns in(1.8)is very complicated.

In this work,we provide an initial investigation that focuses on a few key issues.The rest of this paper is outlined as follows.Section 2 contains the normal form analysis of equations(1.6)and(1.7)by using a new and unified multiple-scale to parameters.The numerical investigations of extended Swift-Hohenberg equation with different broken symmetry terms are carried out in Section 3,where we show that localized states in equations(1.6)-(1.8)exhibit different types of homoclinic snaking,which is different from that of(1.1).In addition,by adding different symmetrybreaking terms in(1.1),we also present the existence of the new round-snakes and round-isolas.Finally,we end the paper with a brief conclusion.

2 Normal Form Analysis

In this section,we will classify the dynamics of the extended Swift-Hohenberg equation with different symmetry-breaking terms by deriving the relationship between the coefficients in the normal form and the parameters in(1.6)and(1.7).

We consider the steady-state solution of equations(1.6)and(1.7)together,that is,equation(1.8),at the same time,by taking the same new rescalings to the following equation:

By expanding u(x,t)as a sum of Fourier modes multiplied by amplitudes that depends on long spatial and temporal scales.Introduce a parameter ε≪ 1 and rescale the parameters

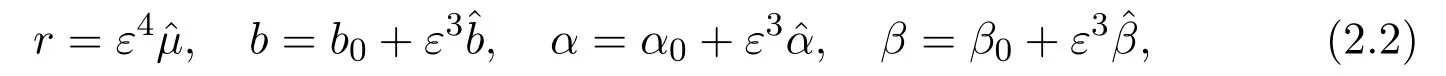
where b0,α0,β0are the values to be determined by the cubic and quadratic coeffi-cients corresponding to q2=0.

Next,we define the large spatial scale X= εx and long time scale T= ε4t,and propose the following ansatz for solution of(1.8):

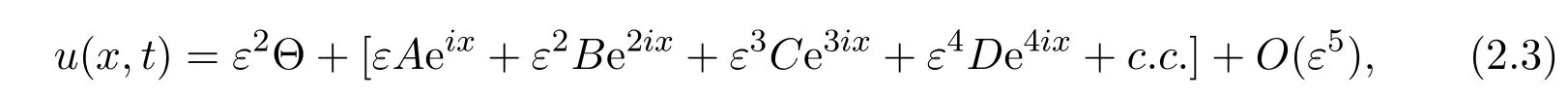
where Θ,A,B,C,D being functions of X and T are all O(1),the higher order terms in ε take the form εnenix+c.c.for n ≥ 5,and “c.c” denotes complex conjugation of the terms preceding it within the brackets.

By substituting the changes(2.2)and(2.3)into(2.1),and collecting the same Fourier dependence enix,for n=0,1,2,3,and writing the higher term as the neglected terms,the results for n=0,1,2,3 are as follows:

At first,we need to solve Θ,B,C in terms of the principle amplitude A from(2.4),(2.6)and(2.7).Writing

substituting them into(2.4),(2.6)and(2.7),we obtain the leading order relations:

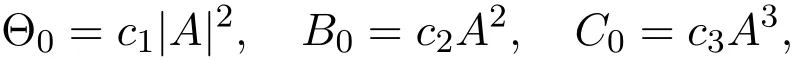
where c1,c2and c3are represented by

respectively.

Next,from(2.4)and(2.6),we have

where the parameters are written by

We now turn to consider(2.5).In fact,this equation contains O(ε3)term and O(ε5)term,and the coefficient of ε3is

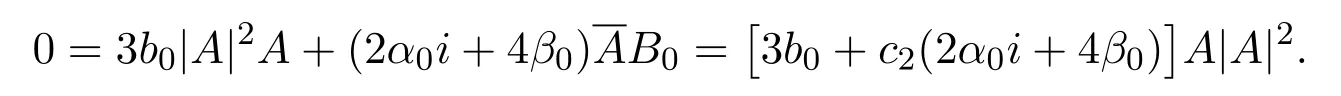
Denote

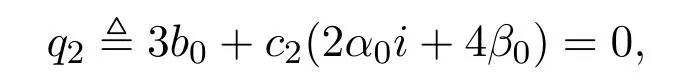
then we have

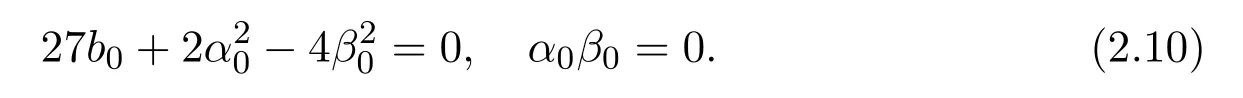
(1)If α0=0,then it follows that

(2)if β0=0,then it follows that(see Figure 1).Obviously,the effects of|α0|and|β0|to|b0|are different.

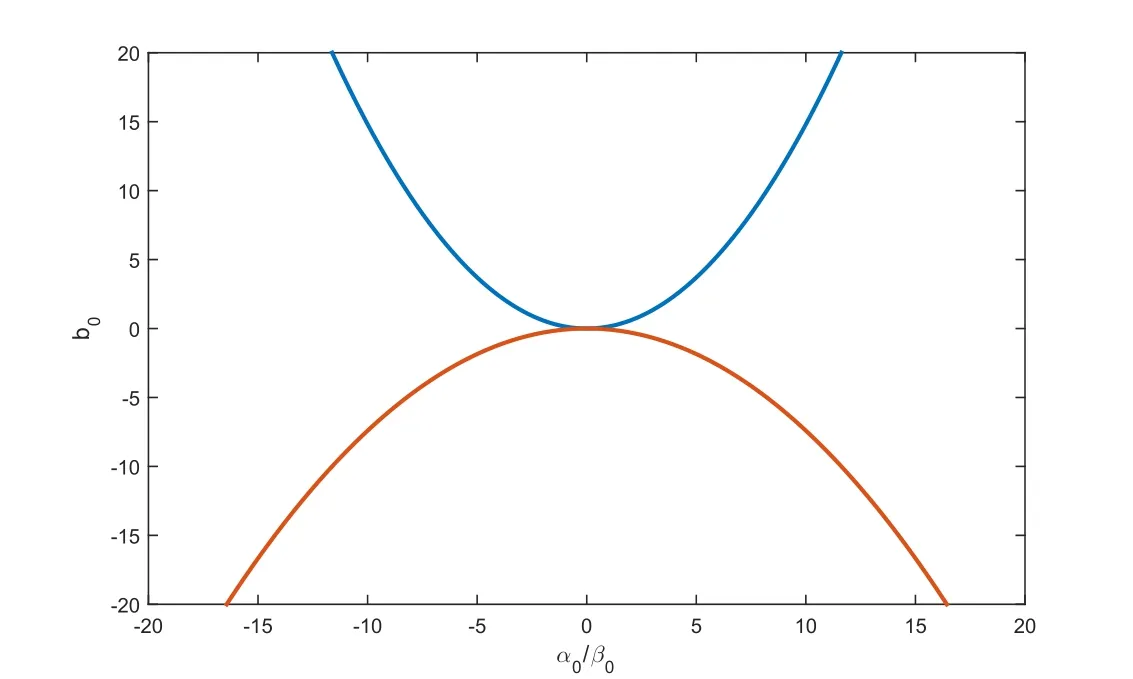
Figure 1:Diagram of b0with α0and β0.

The remaining terms in(2.5)are O(ε5),we can easily obtain a differential equation for the principal amplitude A(X,T):

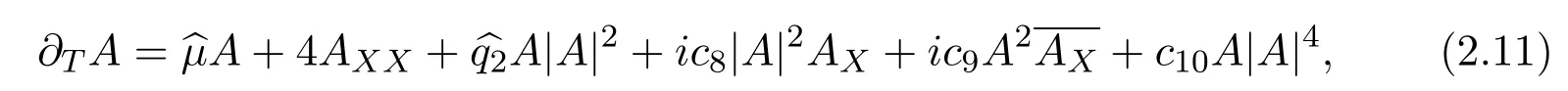
where the parameters are denoted by

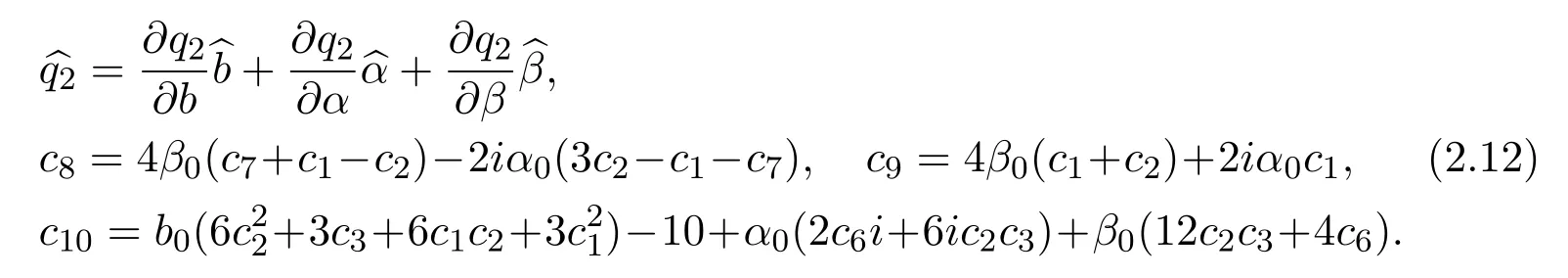
Equation(2.12)is the Ginzburg-Landau approximation,which describes the spatial evolution of amplitude A to the cubic-quintic Swift-Hohenberg equations(1.6)and(1.7)valids near onset in the regions of small criticality.

3 Dynamics of Equilibria

Since we are just concerned about the dynamics of steady-state solutions of equation(1.8),it can be rewritten as a four-dimensional ODE system:

that is

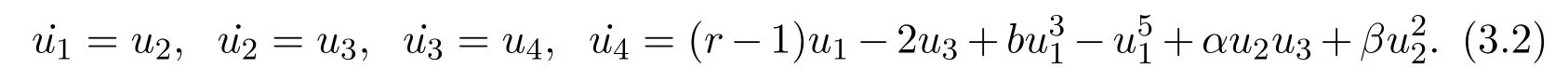
Now we turn to compute the equilibria of system(3.2)by setting

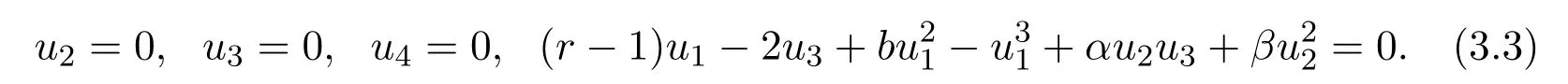
It is easy to obtain the following five equilibria

Take b=2 for simplicity,then the above-mentioned equilibria become:

Due to the high order of perturbation terms,the two perturbation terms αu2u3anddo not effect the location and existence of equilibria.

一是信息技术。对于电气自动化而言，信息技术对其发展发挥了较大的支配作用，其影响是深刻的。信息技术，作为人类开发和利用信息的全部手段，深入到社会经济生活的各个领域。信息技术的进步，为电气自动化的技术创新提供了支持和基础性支撑，而与此同时，电气自动化也为信息技术创新提供了方向。

Let us compute the Jacobian matrix of system(3.2)as follows:

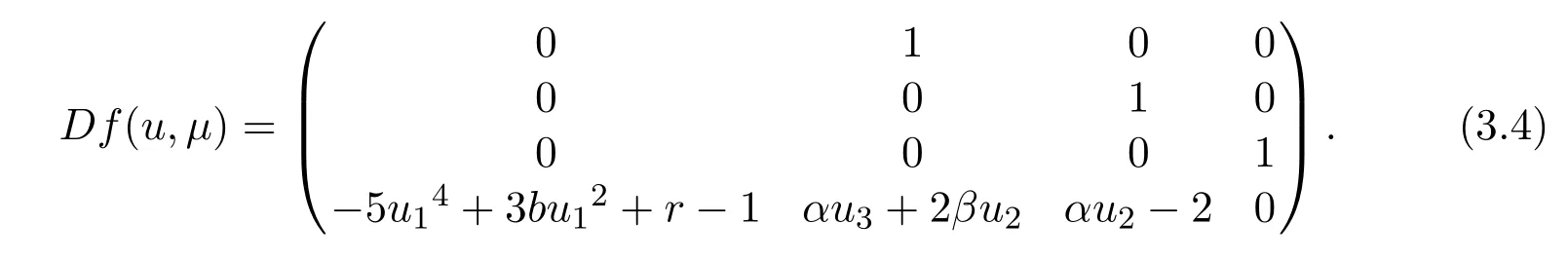
At first,we compute the Jacobian matrix of E1(0,0,0,0),it follows that

then we get the characteristic equation λ4+2λ2− r+1=0,which means thatThere are three cases:

If r=1,then λ3,4=0(double zero eigenvalues),then it undergoes a BT bifurcation.

If we continue the bifurcation from the first equilibrium E1,then we find the existence of two Hopf bifurcation points(H1and H2),two saddle-node bifurcation points(SN)and a pitch-fork bifurcation point(PF)(see Figure 2 for details).

Figure 2:Bifurcation diagram of equilibrium E1.

Now we consider the types of the rest equilibria E2,E3,E4,E5.Similarly,we figure out the characteristic equation

where

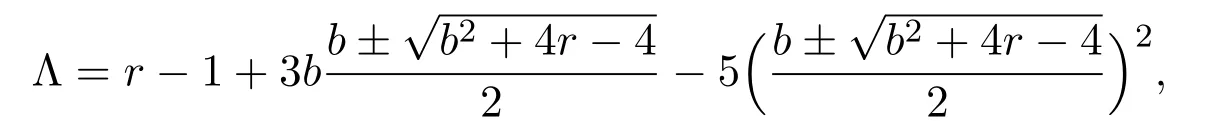
1and Λ2correspond to the equilibria E2,E3and E4,E5,respectively.

Firstly,we consider the characteristic equation λ4+2λ2− Λ1=0 as follows:

(i)If 0＜r＜1,then 0＜Λ1＜1,the corresponding characteristic roots are(that is,a pair of pure imaginary roots)and(a pair of conjugate real roots),which means that the equilibria E2and E3are saddle-center bifurcation points.

(ii)If r=1,here Λ1=0,the characteristic roots become 0(double)and ±and the equilibria E2and E3are BT bifurcation points.

Secondly,we consider the characteristic equationand Λ=there are a pair of pure imaginary rootsand a pair of real roots±which means that the equilibria E4and E5are saddle-center bifurcation points.

4 Numerical Simulations

In this section,we will numerically investigate the behaviors of localized patterns in the Swift-Hohenberg equation with the inclusion of non-reversible or nonk-symmetry terms.For simplicity,we fix b=2.0.Throughout this part we use the software package AUTO07P[8]to trace bifurcation branches of localized states with respect to the primary parameter r.

At first,we consider numerically equation(1.6)with α=0.1 including a symmetrybreaking term αuxuxx,this term destroies the reversible condition R:x → −x,and k-symmetry condition:u→−u,but keeps the variational structure for t and conservative property for x.Then we obtain the S-branches and Z-branches.Note that,each point of those branches are corresponding to an asymmetric localized pattern.See the branches and example solution pro files in Figure 3 for details.

With the increasing of α,the S-branches and Z-branches rotate clockwisely and become smaller as illustrated in Figures 4 and 5.

Next,we are also concerned about the change of snaking when we continue to destroy the k-symmetry and Hamiltonian structure after breaking reversibility in equation(1.8),that is,by adding the non-variational termin(1.6).Then we obtain a new so-called round-snakes as illustrated in Figure 6 and solution pro files in Figure 7.Conversely,if we first continue the parameter β,next continue the parameter α,that is,add αuxuxxin(1.7),then we obtain the snaking branch as shown in Figure 8.

Figure 3:The center panel contains the bifurcation diagram of 1D localized pulses.Example S-branch,Z-branch and their corresponding asymmetric solution pro files of Swift-Hohenberg equations(1.6)at(b,α)=(2.0,0.1).

Figure 4:Evolution of S-branches of Swift-Hohenberg equation(1.6)as α=−0.1,−0.03,0.01,0.05,respectively.The branches rotate clockwisely and become smaller as α increases.

Figure 5:Evolution of Z-branches of Swift-Hohenberg equation(1.6)as α=−0.05,−0.02,0.005,0.01,respectively.The branches rotate clockwisely and become smaller as α increases.

Figure 6:Round-snakes of of Swift-Hohenberg equation(1.8)as α = −0.01 and β =0.01.

Figure 7:Solution pro files in round-snakes of of equation(1.8)as α = −0.01 and β =0.01.

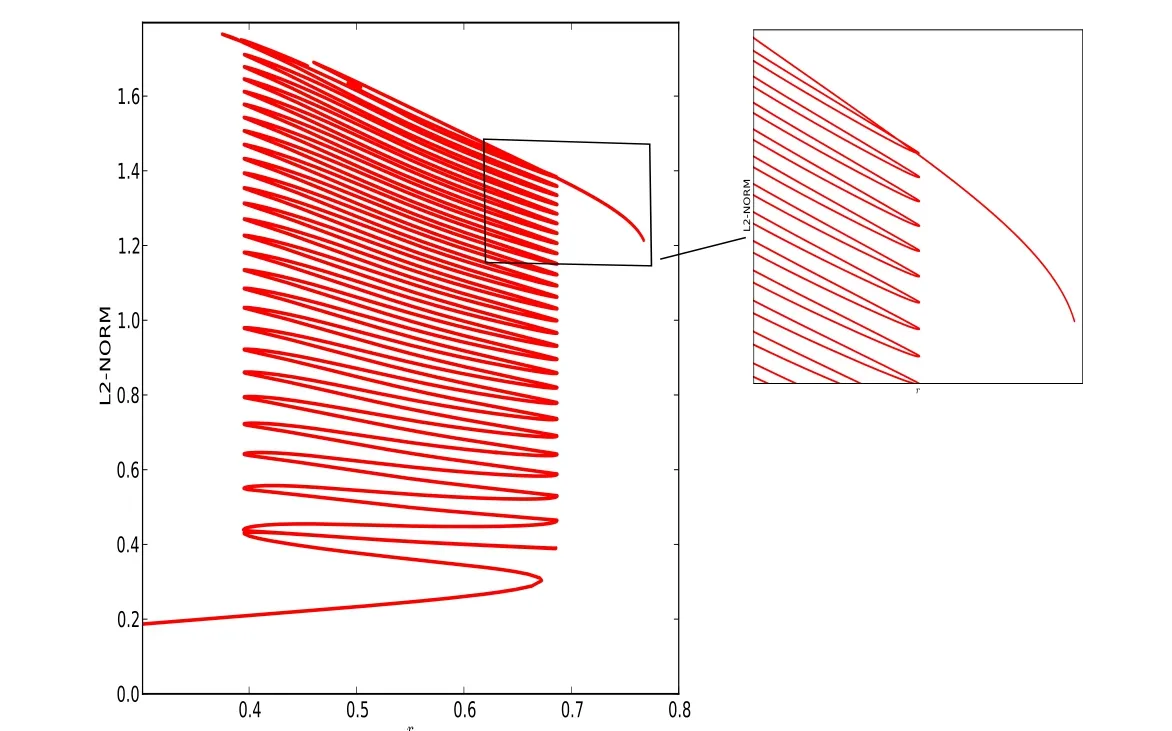
Figure 8:The corresponding snakes of Swift-Hohenberg equation(1.8)when α =0.03 and β =0.05.

Finally,let us add the two broken-symmetry terms at the same time,then(3.6)does not have any symmetry now,and we will see the change of snaking branch.While for quadratic-cubic Swift-Hohenberg equation with γuxxxfor b=2,investigated by[4],a stack of isolas was obtained.So,here we also obtain the existence of isolas of equation(1.8).Unfortunately,we can not find isolas in equation(1.8).However,we can get a stack of isolas in equation(3.7)given below,which is shown in Figures 10 and 11.

Now,we consider the extended cubic-quintic Swift-Hohenberg equation as follows:

and continue it with special parameters,then we get the round-snaking branch with a little deformation.See Figure 9 for details.

Figure 9:Deformed round-snakes of Swift-Hohenberg equation(3.6)at α=0.05.

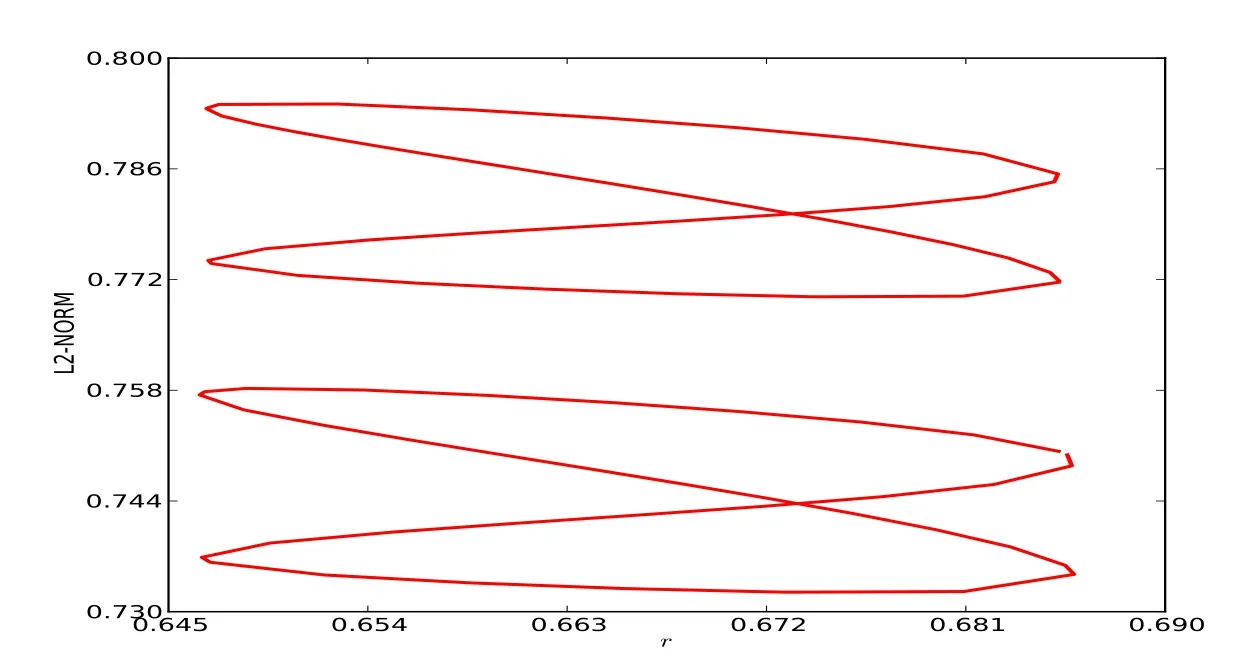
Figure 10:Diagram of isolas of Swift-Hohenberg equation(3.7)at(α,β)=(0.05,0).

Figure 11:Diagram of round-isolas of Swift-Hohenberg equation(3.7)at(α,β)=(0.05,0.05).

Motivated by Knobloch et al.[16],we also demonstrate the existence of isolas of the following Swift-Hohenbeg equation with different non-reversible term:

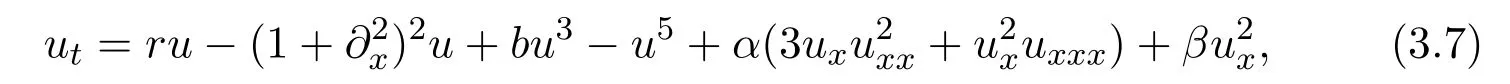
Obviously,the first perturbation termguarantees that(3.7)is a non-reversible,conservative,and k-symmetric system,while the second termis a non-conservative and non-k-symmetric term.

If we take β=0 in(3.7),then it is a non-reversible but conservative and ksymmetric system,then its bifurcation diagram is isolas(see Figure 10 for details).

If we take α=0 in(3.7),then it is a non-k-symmetric system,but respects the reversibility,then its bifurcation diagram is snakes with symmetric solution pro files as illustrated by[12,15].Then we can get S-branches and Z-branches.The Z-branch starts and ends on the same symmetric snake branch while the S-branch connects the two symmetric branches to each other.

Furthermore,we first take α =0.05,next take β =0.05,that is,we first destroy the reversibility but keep k-symmetry,next destroy the conservative property,it then follows that there are a stack of isolas with the increasing size,whose pro files are asymmetric(see Figures 10 and 11).Conversely, first destroy the symmetry k but respect reversibility,then there is a stack of isolas with asymmetric solution pro files,for simplicity,here we omit the details.

In addition,we turn to consider the following Swift-Hohenberg equation

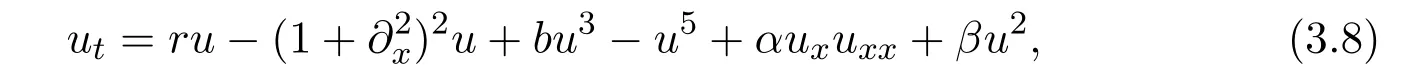
which is a non-reversible,non-k-symmetric but variational system.If we take α=0 and β=0.03 in equation(3.8),that is,just breaking k-symmetry property,then we obtain the following deformed snaking branch(see Figure 12),studied by[12,15].

Figure 12:The corresponding snaking branch of Swift-Hohenberg equation(3.8)when β=0.03.

In addition,we are also interested in the change of bifurcations when we continue destroying reversible property after the k-symmetry and Hamiltonian structure.By taking β =0.03 with α =0.1,we obtain the following new snaking,the so-called round-snaking,shown in Figures 13 and 14,which presents the role of reversibility.In fact,now the ODE system of equation(3.8)is a non-reversible,non-conservative and non-k-symmetric system.

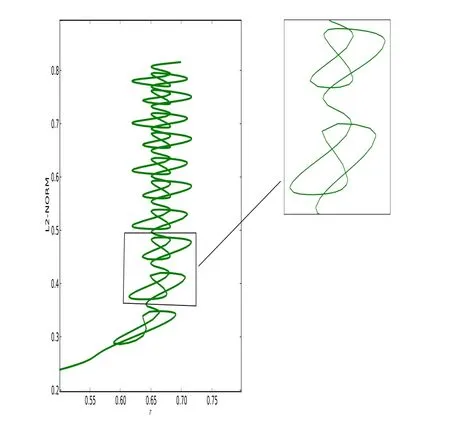
Figure 13:The round-snaking of Swift-Hohenberg equation(3.8)when β =0.03 and α =0.1.

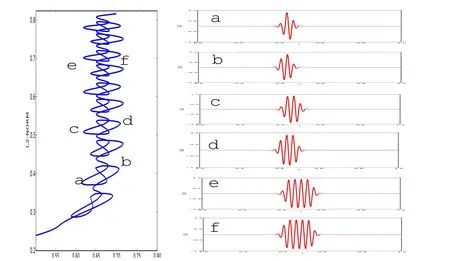
Figure 14:The corresponding example pro files of round-snaking of Swift-Hohenberg equation(3.8)when β =0.03 and α =0.1.

Note that,we add two different quadratic terms:and βu2to equation(1.6),which all break k-symmetry and respect the symmetry R,but the first term is nonvariational,the second term is variational.According to Figures 7 and 14,we know that the two snaking branches are similar,just presenting the same kind of deformed round-snaking.If we keep β =0.05,and continue the parameter α,that is,taking α=0.01,0.1,0.2,0.3,0.4,0.45,respectively,then we know about the change of round-snakes(see Figure 15 for details).

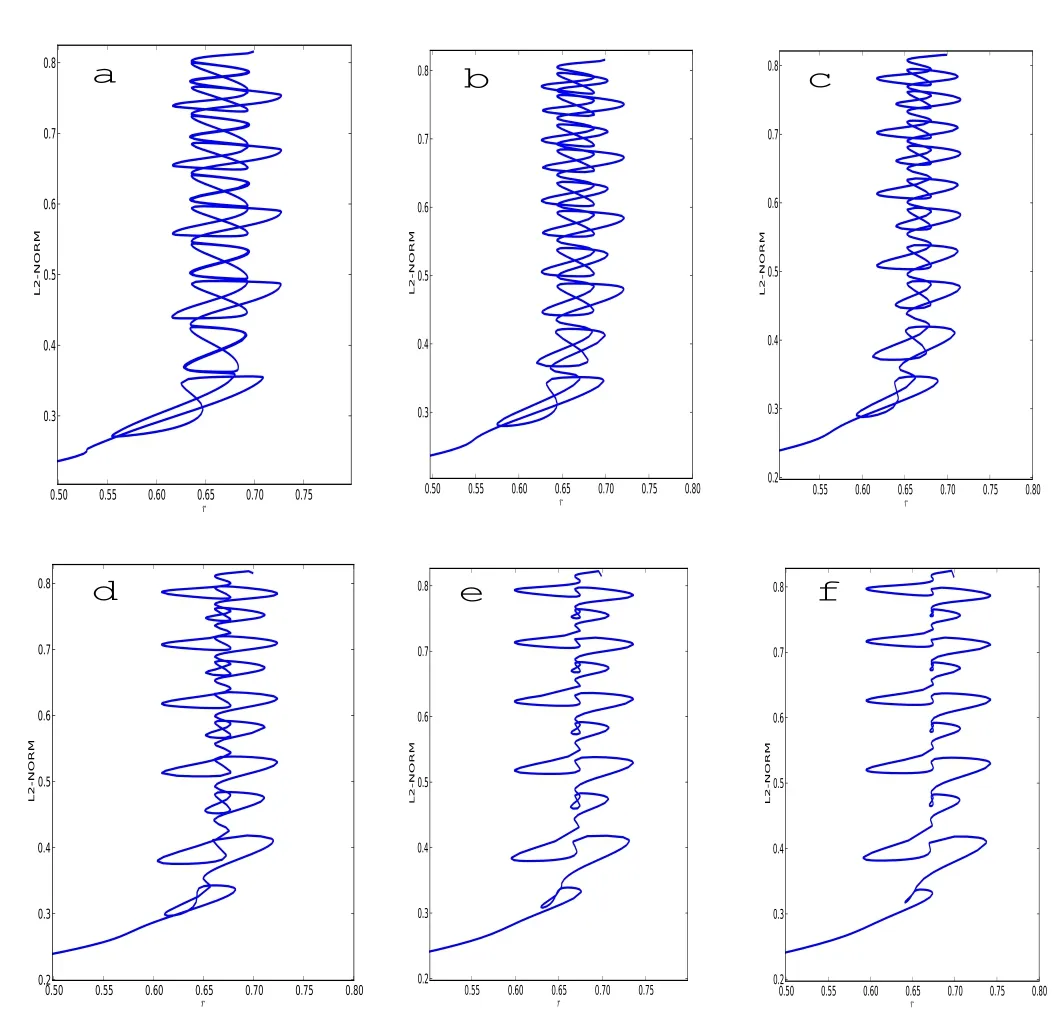
Figure 15:Diagrams of Swift-Hohenberg equation(3.8)while keeping β=0.05 fixed with α=0.01,0.1,0.2,0.3,0.4,0.45 corresponding to a,b,c,d,e,f,respectively.The figure-eights of snakes become smaller and smaller as α increases until they vanish when α ＞ 0.45.

5 Conclusions

In this work,we obtain the normal form of cubic-quintic Swift-Hohenberg equation with two kinds of broken symmetry terms by using a new and unified multiplescale method,and show its different bifurcation diagrams of localized solutions.The role of different symmetry-breaking terms,that is,non-reversible,non-k-symmetric,and non-conservative terms,are presented by numerically simulations.Meanwhile,a new kind of the so-called round-snaking bifurcation and round-isolas bifurcation was obtained.That is,when the reversibility and k-symmetry are broken,the system will undergoes new round-snake and round-isola bifurcations.So,the study of the formation of these branches will be a fruitful area for future work.

AcknowledgementWe are grateful to Professor Bjorn Sandstede for his helpful suggestions.

[1]S.Blanch flower,Magnetohydrodynamic convectons,Physica A,261(2009),936-972.

[2]M.Beck,J.Knobloch,D.J.B.Lloyd,B.Sandstede and T.Wagenknecht,Snakes,ladders,and isolas of localized patterns,SIAM J.Math.Anal.,41(2009),936-972.

[3]Y.Astrov and Y.Logvin,Formation of clusters of localized states in a gas discharge system via a self-completion scenario,Phys.Rev.Lett.,79(1997),2983-2986.

[4]J.Burke,S.M.Houghton and E.Knobloch,Swift-Hohenberg equation with broken symmetry,Phys.Rev.E,80(2009),036202.

[5]J.Burke and E.Knobloch,Homoclinic snaking:structure and stability,Chaos,17(2007),037102.

[6]S.J.Chapman and G.Kozyreff,Exponential asymptotics of localised patterns and snaking bifurcation diagrams,Physica D,238(2009),319-354.

[7]J.H.P.Dawes,The emergence of a coherent structure for coherent structures:localized states in nonlinear systems,Phil.Trans.R.Soc.A,368(2010),3519-3534.

[8]E.J.Doedel and B.E.Oldeman,AUTO-07P:Continuation and bifurcation software for ordinary differential equations,Technical report,Concordia University,2009.

[9]E.Knobloch,Spatially localized structures in dissipative systems:open problems,Nonlinearity,21(2008),T45-T60.

[10]S.M.Houghton and T.Wagenknecht,Multi-pulses in the Swift-Hohenberg equation with broken symmetry,In preparation(2012).

[11]J.Knobloch,D.J.B.Lloyd,B.Sandstede and T.Wagenknecht,Isolas of 2-pulse solutions in homoclinic snaking scenarios,J.Dyn.Diff.Eqns.,23(2011),93-114.

[12]S.H.Houghton and E.Knobloch,Swift-Hohenberg equation with broken cubic-quintic nonlinearity,Phys.Rev.,84(2011),016024,1-10.

[13]J.Knobloch,T.Rieß and M.Vielitz,Nonreversible homoclinic snaking,Dynamical Systems,26(2011),335-365.

[14]B.Sandstede,Y.C.Xu,Snakes and isolas in non-reversible conservative systems,Dynamical Systems,27(2012),317-329.

[15]E.Makrides and B.Sandstede,Predicting the bifurcation structure of localized snaking patterns,Physica D,268(2014),59-78.

[16]J.Knobloch,M.Vielitz and T.Wagenknecht,Nonreversible perturbations of homoclinic snaking scenarios,Nonlinearity,25(2012),3469-3485.

[17]G.Kozyreffand S.J.Chapman,Asymptotics of large bound states of localised structures,Phys.Rev.Lett.,97(2006),044502.

[18]J.D.M.Rademacher,Homoclinic orbits near heteroclinic cycles with one equilibrium and one periodic orbit,J.Diff.Eqns.,218(2005),390-443.

[19]J.D.M.Rademacher,Lyapunov-Schmidt reduction for unfolding heteroclinic networks of equilibria and periodic orbits with tangencies,J.Diff.Eqns.,249(2010),305-348.

[20]J.Burke,E.Knobloch,Normal form for spatial dynamics in the Swift-Hohenberg eqaution,Discrete and Continous Dynamical Systems,87:supp.(2007),170-180.

[21]J.Burke,E,Knobloch.Snakes and ladders:Localized states in the Swift-Hohenberg equation,Phy.Lett.A,360(2007),681-688.

[22]J.Burke and J.H.P.Dawes,Localized states in the Swift-Hohenberg equation,SIAM J.Appl.Dyn.Syst.,11(2012),261-284.

[23]P.D.Woods and A.R.Champneys,Heteroclinic tangles and homoclinic snaking in the unfolding of a degenerate reversible Hamiltonian Hopf bifurcation,Physica D,129(1999),147-170.

[24]Uwe Thiele,Andrew J.Archer,and Mark J.Robbins,Localized states in the conserved Swift-Hohenberg equation with cubic nonlinearity,Phys.Rev.E,87(2013),042915.