GLOBAL DYNAMICS OF A PREDATOR-PREY MODEL WITH PREY REFUGE AND DISEASE∗†

Zaowang Xiao,Zhong Li

(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)

1 Introduction

Predator-prey model is one of the basic models between different species in nature.These models have been studied extensively and many excellent results have been obtained(see[1,2]).On the other hand,the effect of disease in ecological system is an important topic from mathematical as well as ecological point of view.After the work of Kermack-McKendrick[3]on SIRS(susceptible-infected-removedsusceptible)systems,many authors have investigated the dynamical behavior of epidemiological models.Chattopadhyay and Arino[4]proposed a predator-prey epidemiological model with disease spreading in prey.They assumed that the sound prey population grows according to a logistic law involving the whole prey population,and discussed the positivity,uniqueness,boundedness of the solutions and the existence of supercritical Hopf bifurcation.Haque et al[5]investigated a Lotka-Volterra type predator-prey model with a transmissible disease in the predator species.They aussumed that the sound and infected predators can hunt the prey and studied the stability of system.

Sun and Yuan[6]proposed the following predator-prey model with disease in the predator

where x(t),S(t)and I(t)represent the densities of the prey,susceptible(sound)predator and the infected predator population at time t,respectively.They assumed that there is a spread of disease in predator and only the susceptible predators have ability to capture prey.They investigated the boundedness of solution and global asymptotical stability of the equilibriums.

On the other hand,prey species makes use of refuges to decrease predation risk,here refuge means a places or situations where predation risk is somehow reduced.Ma et al[7]studied the following predator-prey model with prey refuges and a class of functional responses

where the term φ(X)represents the functional response of the predator population.They obtained the local asymptotical stability of equilibrium point and showed that the refuges used by prey can increase the equilibrium density of prey population but decrease that of predator.Ma et al.[8]further studied the influence of prey refuge and density dependent of predator species on the traditional Lotka-Volterra model.Huang,Chen and Li[9]studied the influence of prey refuge on a predatorprey model with Holling type III response function.In[10],a global analysis of a Holling type II predator-prey model with a constant prey refuge was presented.Ma et al[11]and Chen,Chen and Wang[12]studied a Lotka-Volterra predatorprey model incorporating a prey refuge and predator mutual interference.For more details in this direction,please see[13,14].

However,there are still seldom scholars investigating the predator-prey model with prey refuge and disease in predator.More precisely,we study the global stability of the following model

where x(t),S(t)and I(t)represent the densities of the prey,susceptible(sound)predator and the infected predator population at time t,respectively with initial conditions x(0)＞0,S(0)＞0,I(0)＞0.All the parameters are positive constants and 0＜m＜1.The disease incidence follows the simple law of mass action incidence βS(t)I(t)with β being the transmission coefficient;d1≤ d2;mx(t)is the capacity of a refuge at time t.

The organization of this paper is as follows.In Section 2,we study the stability of the equilibriums of system(1.3).In Section 3,numerical simulation is presented to illustrate the feasibility of our main results.In the last section,we give a brief discussion.

2 Main Results

In this section,we investigate the local and global stability of system(1.3).

Similar to the proof of[6],we have the following lemma.

Lemma 2.1All solutions of system(1.3)with a positive initial data will remain positive and uniformly bounded.

We can easily calculate that system(1.3)always has a trivial equilibrium E0(0,0,0)and a predator-extinction equilibrium E (K,0,0).If

holds,then system(1.3)has a disease-free equilibrium E2(x1,S1,0),where x1=

Further,for the unique endemic-coexistence equilibrium E∗(x∗,S∗,I∗)of system(1.3),x∗,S∗and I∗satisfy the following equations

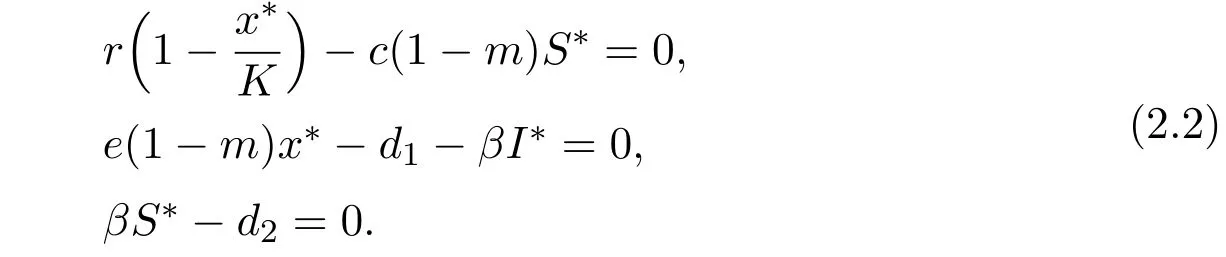
From the above equation,if

hold,then x∗,S∗and I∗are positive and satisfy

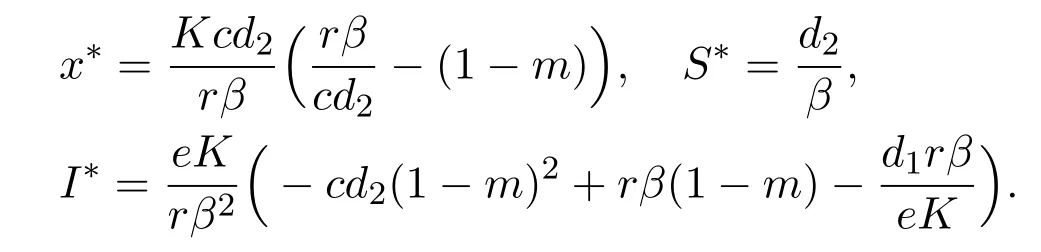
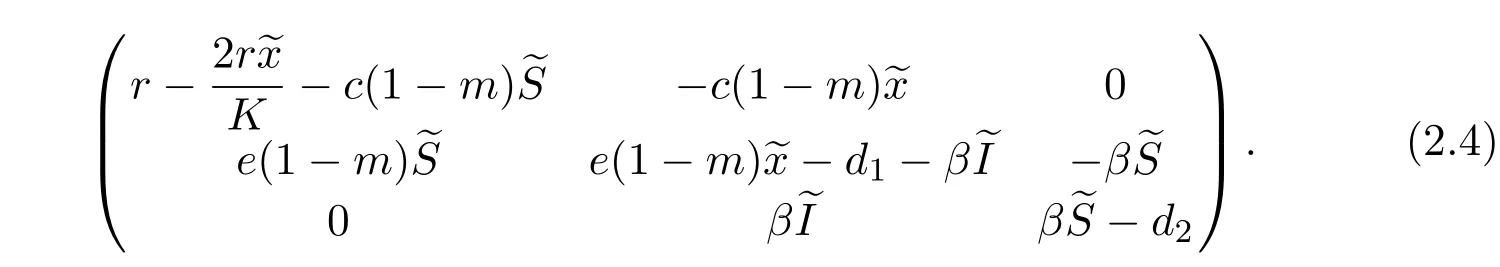
It is easy to prove that the equilibrium E0(0,0,0)is always unstable.

For the predator-extinction equilibrium E1(K,0,0),the Jacobian matrix is given by

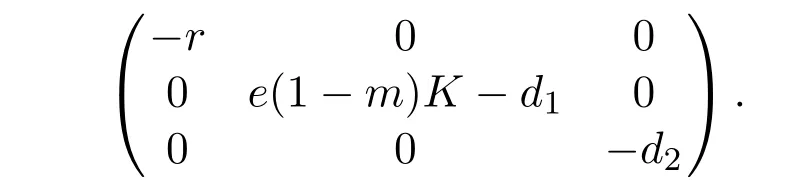
For the disease-free equilibrium E2(x1,S1,0),the Jacobian matrix is given by

Then the characteristic equation is

By calculation,βS1−d2＜ 0 is equivalent to cd2(1−m)2−rβ(1−m)+＞0.Hence,the disease-free equilibrium E2(x1,S1,0)is locally asymptotically stable if and only if cd2(1−m)2−rβ(1−m)+＞0.

Again,for the unique endemic-coexistence equilibrium E∗(x∗,S∗,I∗),the Jacobian matrix is given by

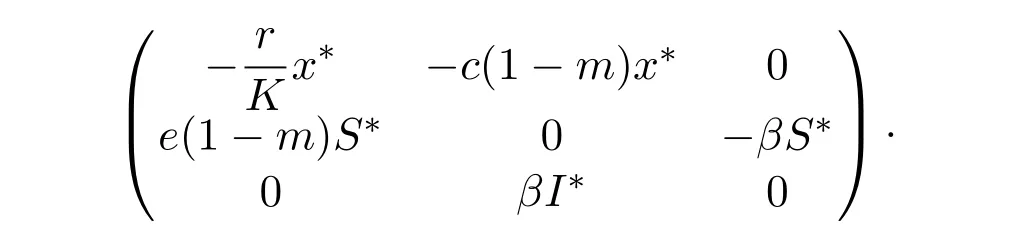
Then the characteristic equation is

Then we have the following result.

Lemma 2.2

(i)The trivial equilibrium E0(0,0,0)is unstable.

By the definition of x∗,we have x∗＜ K.It follows from the second equation of(2.2)that 1−m＞,that is,the existence of E∗(x∗,S∗,I∗)implies that 1−m＞holds.

De fine

Let∆1=rβ(rβ −).

(i)If z2＜1,then H(z)＞0 for＜z＜z1and z2＜z＜1,H(z)＜0 for z1＜z＜z2.

(ii)If z1＜1≤z2,then H(z)＞0 for＜z＜z1,H(z)＜0 for z1＜z＜1.

(iii)If z1≥1,then H(z)＞0 for＜z＜1.

By analyse,we have the following results.

Proposition 2.1If rβ ＞and＜1,then

(i)z2＜ 1 if and only if

(ii)z1＜1≤z2if and only if one of the following conditions hold:

(iii)z1≥ 1 if and only if

Proof(i)z2＜1 is equivalent toHence,ifhold,then the conclusion(i)holds.

The proofs of(ii)and(iii)are similar to that of(i)and we omit the detail here.This completes the proof of Proposition 2.1.

From Proposition 2.1,we have the following proposition.

Poposition 2.2Proposition 2.1 is equivalent to the following statements.

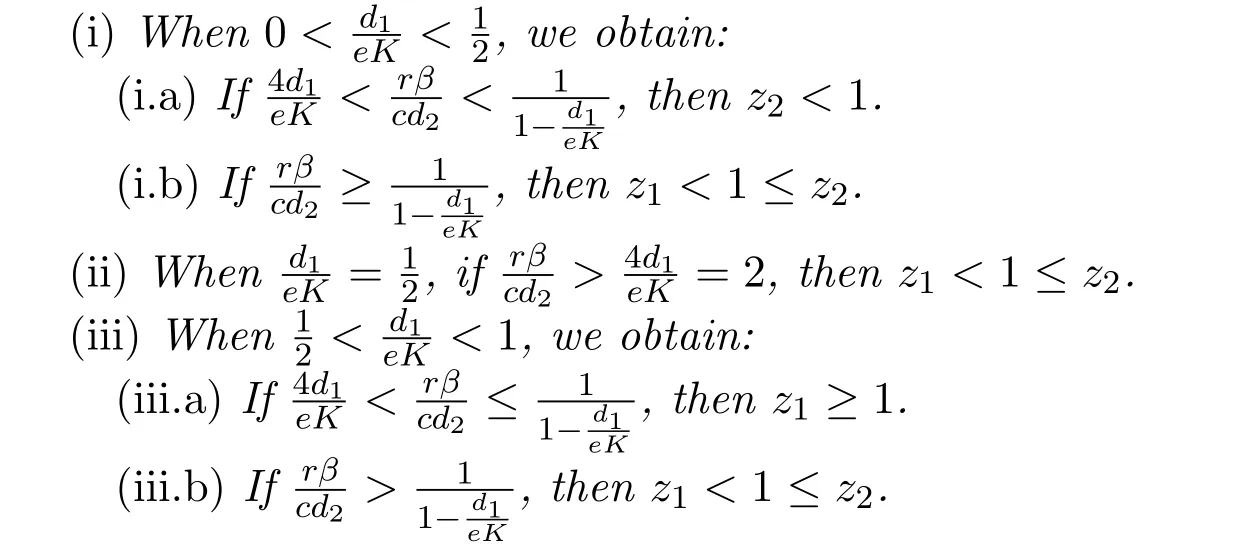
ProofNote thatfor 0＜ x＜ 1.It follows from Proposition 2.1 thatThen

The proofs of(ii)and(iii)are similar to that of(i)and we omit the detail here.This completes the proof of Proposition 2.2.

By the above discussion and Propositions 2.1 and 2.2,we have the following result.

Proposition 2.3Equation(2.5)has the following result.

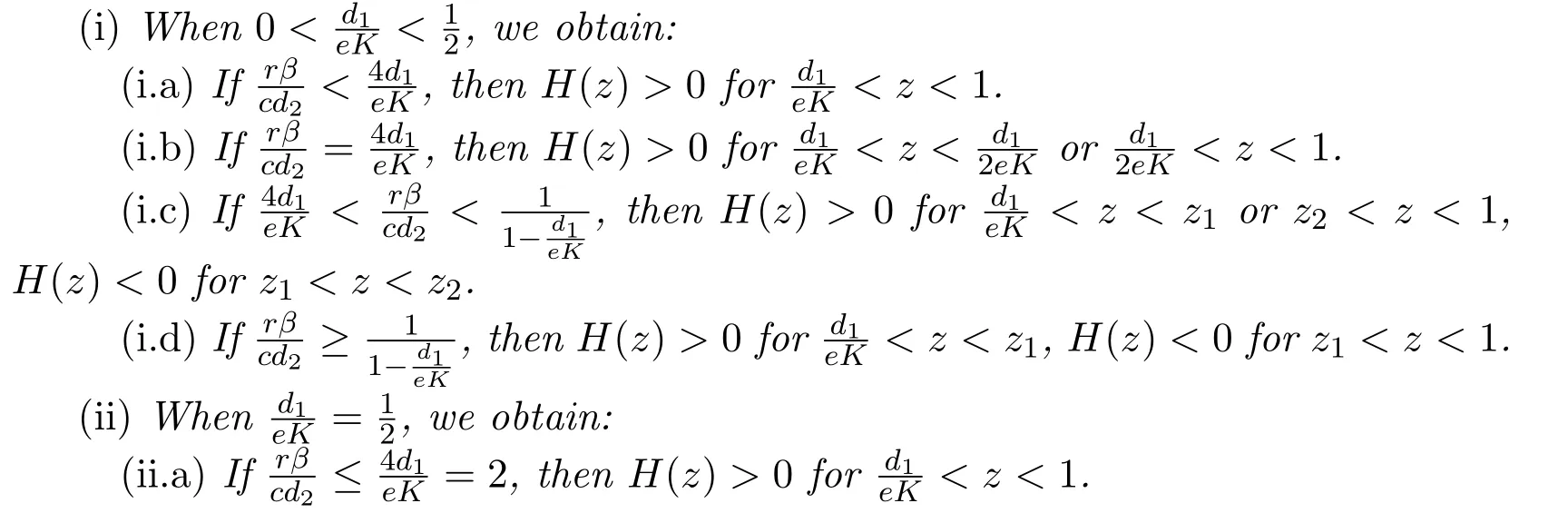
Next we show the global stability of equilibrium of system(1.3),and obtain the following lemmas.

Lemma 2.3If the predator-extinction equilibrium E1(K,0,0)is locally asymptotically stable,then E1(K,0,0)is globally asymptotically stable.

ProofConsider the following Lyapunov function

Calculating the derivative of V along the solution(x(t),S(t),I(t))of system(1.3),we have

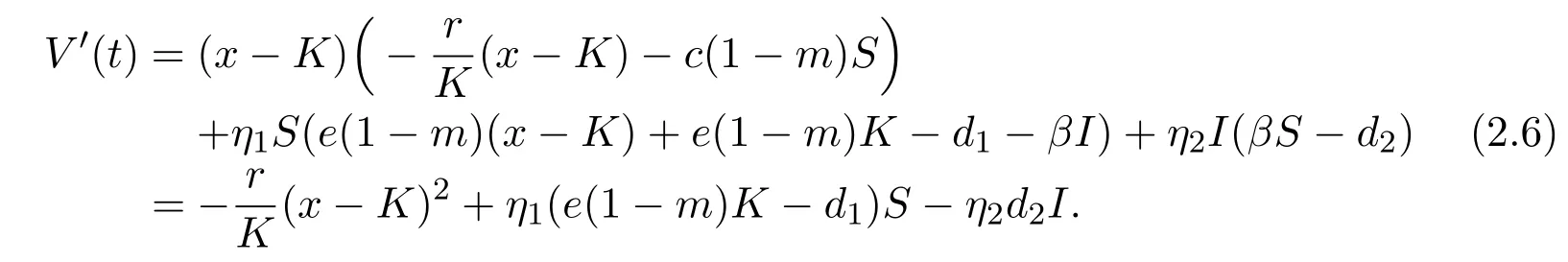
It follows from Lemma 2.2 that e(1−m)K−d1＜0.Then V′(t)＜0 for all(x,S,I)≠(K,0,0).By the Lyapunov-LaSalle invariance principle[15],E1(K,0,0)is globally asymptotically stable.This completes the proof of Lemma 2.3.

Lemma 2.4If the disease-free equilibrium E2(x1,S1,0)is locally asymptotically stable,then E2(x1,S1,0)is globally asymptotically stable.

ProofDe fine a Lyapunov function as follows

where ηi=,i=1,2.

Calculating the derivative of V along the solution(x(t),S(t),I(t))of system(1.3),we have

It follows from Lemma 2.2 that βS1− d2＜ 0.LetThen it follows from(2.7)that

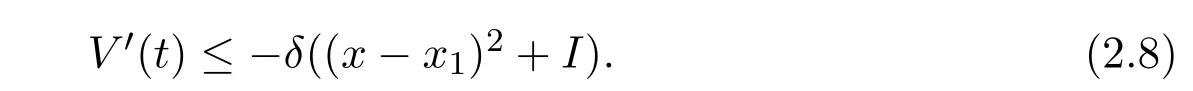
Thus V(t)is nonincreasing.From Lemma 2.1,(x−x1)2and I are bounded.On the other hand,it is easy to see that x′(t)and I′(t)are bounded.Therefore,(x − x1)2and I are uniformly continuous on[0,+∞).Integrating both sides of(2.8)over the interval[0,+∞),we have

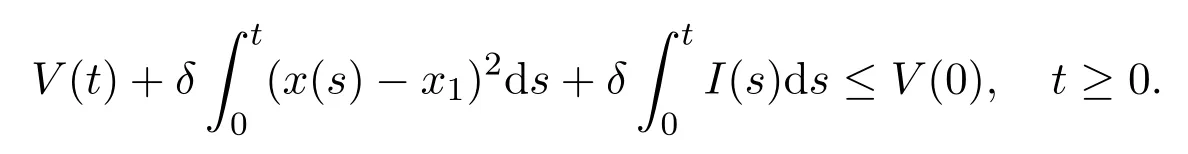
Therefore,V(t)is bounded on[0,+∞)and satisfies

It follows from the above inequality that(x(t)−x1)2∈ L1[0,+∞)and I(t)∈L1[0,+∞).By Barbalat’s lemma[16],we conclude that

so

From the first equation of system(1.3)and the above equality,we have

Hence,

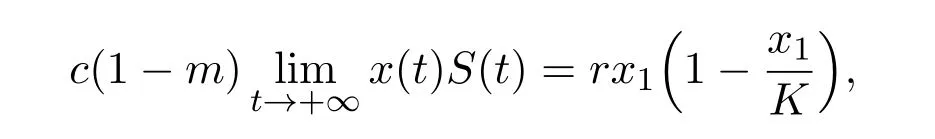
that is

Then,from(2.9)-(2.11),E2(x1,S1,0)is globally asymptotically stable.This completes the proof of Lemma 2.4.

Lemma 2.5If the unique endemic-coexistence equilibrium E∗(x∗,S∗,I∗)is locally asymptotically stable,then E∗(x∗,S∗,I∗)is globally asymptotically stable.

ProofDe fine a Lyapunov function as follows

where ηi=,i=1,2.

Calculating the derivative of V along the solution(x(t),S(t),I(t))of system(1.3),we obtain

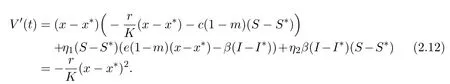
Thus V(t)is nonincreasing.By Lemma 2.1,(x − x∗)2is bounded.On the other hand,it is easy to see that x′(t)is bounded.Therefore,(x − x∗)2is uniformly continuous on[0,+∞).Integrating both sides of(2.12)over the interval[0,+∞),we have

Hence,V(t)is bounded on[0,+∞)and satisfies∫

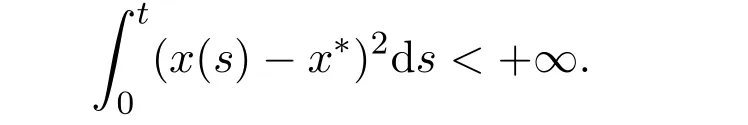
The above inequality implies that(x(t)− x∗)2∈ L1[0,+∞).By Barbalat’s lemma[16],we have

so

It follows from the first equation of system(1.3)and the above equality that

Hence,

that is

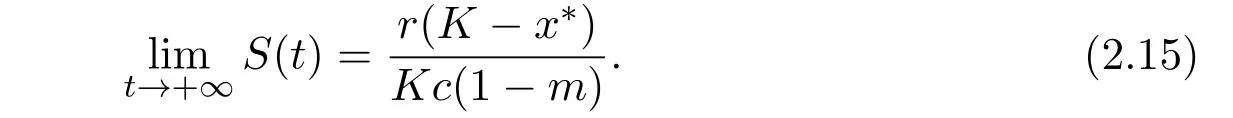
By the definition of x∗,we haveThen,from(2.15),we obtain

From the second equation of system(1.3)and(2.16),we have

Hence,from(2.14)and(2.16),we obtain

that is

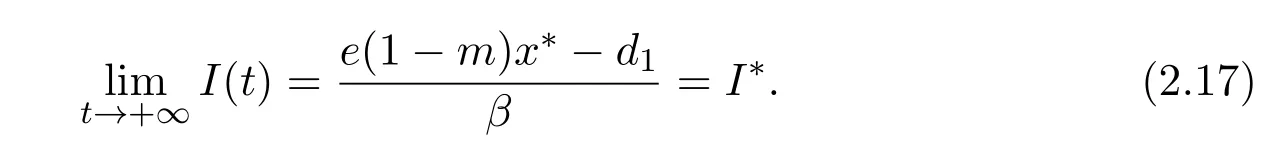
Therefore,by(2.14),(2.16)and(2.17),E∗(x∗,S∗,I∗)is globally asymptotically stable.This completes the proof of Lemma 2.5.

Now,we give the main result of this section.Let z=1−m in(2.5).According to the above analysis and summarizing Propositions 2.1-2.3 and Lemmas 2.2-2.5,we obtain the following theorem.

Theorem 2.1

3 Numerical Simulations

In this section we give some numerical simulations of systems(1.3).We consider the following system

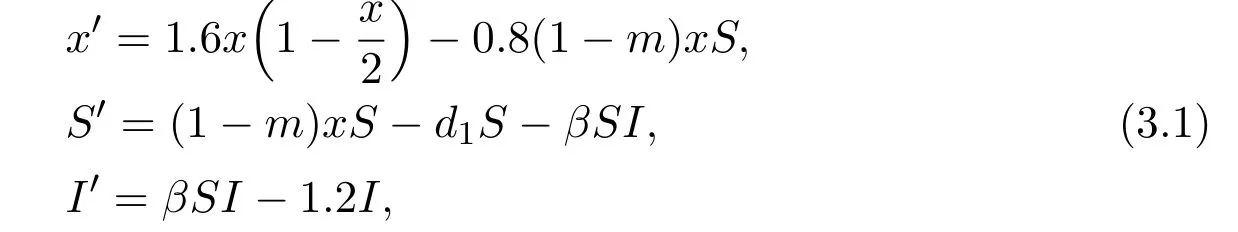
where r=1.6;K=2;c=0.8;e=1;d2=1.2.

When d1=1.5,0.5＜=0.75 ＜ 1.Let β =3,thenIt follows from Theorem 2.1(ii.b)that the unique endemic-coexistence equilibrium E∗(x∗,S∗,I∗)is globally asymptotically stable for all 0 ＜ m ＜ 0.081(see Figure 1(b)),the disease-free equilibrium E2(x1,S1,0)is globally asymptotically stable for all 0.081＜m＜0.25(See Figure 1(c)),and the predator-extinction equilibrium E1(2,0,0)is globally asymptotically stable for all 0.25＜m＜1(See Figure 1(d)).

When d1=1,Let β =1.5,thenIt follows from Theorem 2.1(iii.b)that the unique endemic-coexistence equilibrium E∗(x∗,S∗,I∗)is globally asymptotically stable for all 0＜m＜0.309(see Figure 2(b)),the diseasefree equilibrium E2(x1,S1,0)is globally asymptotically stable for all 0.309＜m＜0.5(see Figure 2(c)),and the predator-extinction equilibrium E1(2,0,0)is globally asymptotically stable for all 0.5＜m＜1(see Figure 2(d)).

When d1=0.4,=0.2 ＜ 0.5.Let β =0.6,then=0.8＜=1＜=1.25.It follows from Theorem 2.1(iv.c)that the disease-free equilibrium E2(x1,S1,0)is globally asymptotically stable for all 0＜m＜0.276 or 0.724＜m＜0.8(see Figures 3(b)and 3(d)),the unique endemic-coexistence equilibrium E∗(x∗,S∗,I∗)is globally asymptotically stable for all 0.276 ＜ m ＜ 0.724(see Figure 3(c)),and the predator-extinction equilibrium E1(2,0,0)is globally asymptotically stable for all 0.8＜m＜1(see Figure 3(e)).

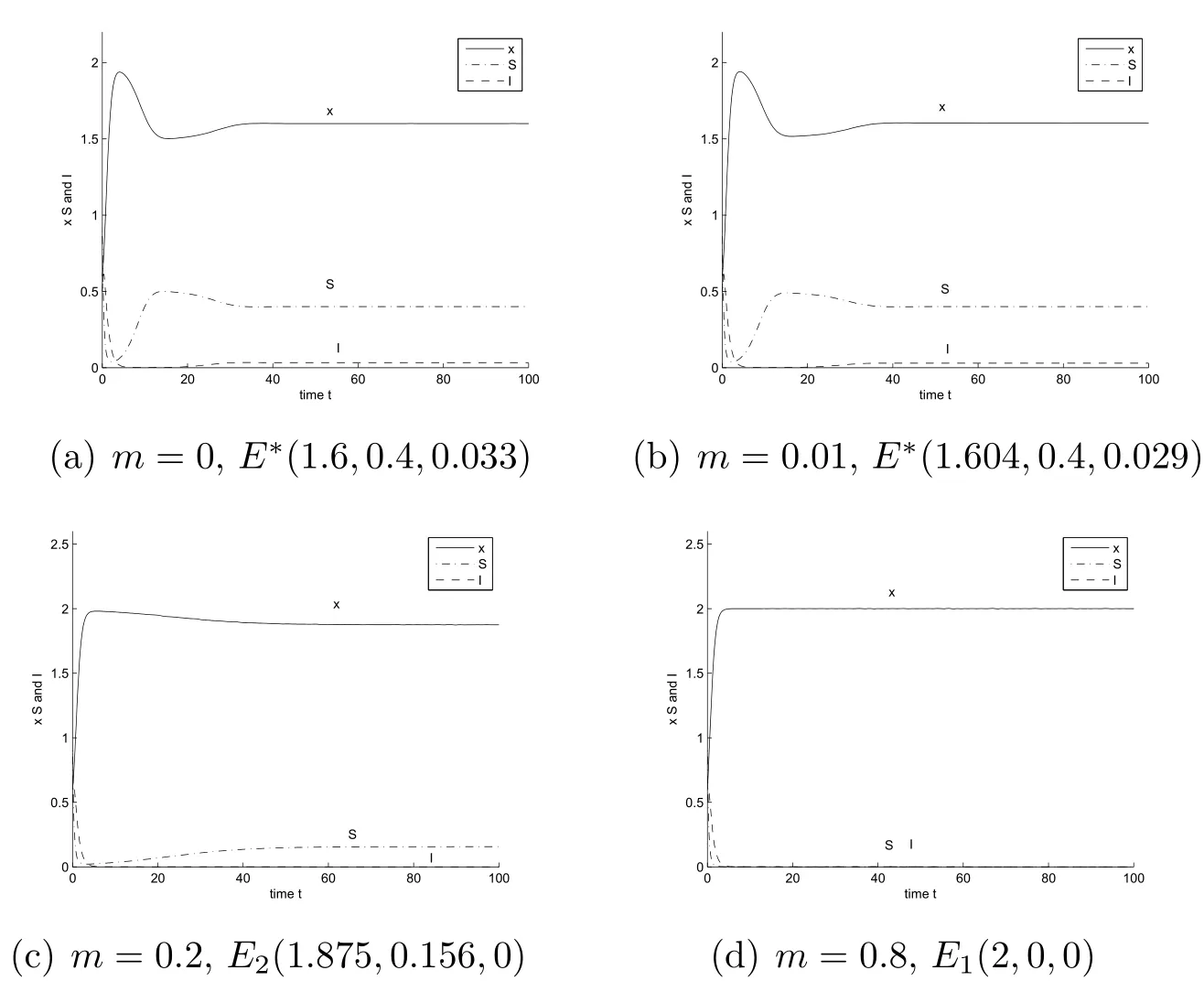
Figure 1:Dynamics behavior of system(3.1)with d1=1.5;β=3.

Figure 2:Dynamics behavior of system(3.1)with d1=1;β=1.5.

Figure 3:Dynamics behavior of system(3.1)with d1=0.4;β=0.6.

4 Discussion

In this paper,we study the global dynamics of a predator-prey model with prey refuge and disease in the predator.We show that prey refuge palys an important role in the dynamics of a predator-prey system(1.3).Form the above results,if the refuge m is sufficiently small,then the dynamics behavior of system is accordant with the corresponding system without prey refuges.By decreasing the value of natural death rate of the susceptible predator d1,the dynamics behavior of system becomes complicated,that is the global stable equilibrium may be changed by increasing the value of refuges m.This shows that prey refuge palys an important role in the dynamics behavior of system(1.3).

[1]Y.Kuang,Delay Differential Equations with Applications in Population Dynamics,Academic Press,New York,1993.

[2]K.Gapalsamy,Stability and Oscillations in Delay Equations of Population Dynamics,Kluwer Academic Publishers,London,1992.

[3]W.Kermack,A.McKendrick,A contribution to the mathematical theory of epidemics,Proc.R.Soc.Lond.,115(1927),700-721.

[4]J.Chattopadhyay,O.Arino,A predator-prey model with disease in the prey,Nonlinear Anal.TMA,36(1999),747-766.

[5]M.Haque,S.Sarwardi,S.Preston,E.Venturino,Effect of delay in a Lotka-Volterra type predator-prey model with a transmissible disease in the predator species,Math.Biosci.,234(2011),47-57.

[6]S.L.Sun,C.D.Yuan,On the analysis of predator-prey model with epidemic in the predator,J.Biomath.,21(2006),97-104.

[7]Z.H.Ma,W.L.Li,Y.Zhao,W.T.Wang,H.Zhang,Z.Z.Li,Effects of prey refuges on a predator-prey model with a class of functional response:the role of refuges,Math.Biosci.,218(2009),73-79.

[8]Z.H.Ma,S.F.Wang.W.Li,Z.Z.Li,The effect of prey refuge in a patchy predator-prey system,Math.Biosci.,243(2013),126-130.

[9]Y.Huang,F.Chen,Z.Li,Stability analysis of a prey-predator model with Holling type III response function incorporating a prey refuge,Appl.Math.Comput.,182(2006),672-683.

[10]G.Y.Tang,S.Y.Tang,R.A.Cheke,Global analysis of a Holling type II predator-prey model with a constant prey refuge,Nonlinear Dyn.,76(2014),635-647.

[11]Z.Z.Ma,F.D.Chen,C.Q.Wu,W.L.Chen,Dynamic behaviors of a Lotka-Volterra predator-prey model incorporating a prey refuge and predator mutual interference,Appl.Math.Comput.,219(2013),7945-7953.

[12]L.J.Chen,F.D.Chen,Y.Q.Wang,In fluence of predator mutual interference and prey refuge on Lotka-Volterra predator-prey dynamics,Commun.Nonlinear Sci.Numer.Simulat.,18(2013),3174-3180.

[13]R.Z.Yang,C.R.Zhang,Dynamics in a diffusive predator-prey system with a constant prey refuge and delay,Nonlinear Anal.RWA,31(2016),1-22.

[14]J.Ghosh,B.Sahoo,S.Poria,Prey-predator dynamics with prey refuge providing additional food to predator,Chaos,Solitons Fractals,96(2015),110-119.

[15]J.K.Hale,Ordinary Differential Equations,Krieger,Malabar,FL,1980.

[16]I.Barbalat,Systems d’equations differential d’oscillations nonlinearities,Rev.Roumaine Math.Pure Appl.,4:2(1959),267-270.