NONEXISTENCE OF POSITIVE SOLUTIONS FOR A FOUR-POINT BOUNDARY VALUE PROBLEM FOR FRACTIONAL DIFFERENTIAL EQUATION∗†

Chunfang Shen

(College of Math.and Statistics,Hefei Normal University,Hefei 230061,Anhui,PR China)

1 Introduction

In this paper,we consider the nonexistence of the positive solution for the following boundary value problem of differential equation involving the Caputo’s fractional order derivative

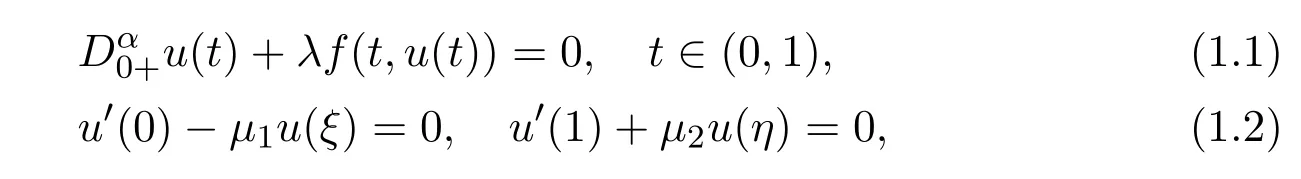
where 1＜α≤2,0≤ξ≤η≤1,0≤µ1,µ2≤1 and satisfy the following conditions:

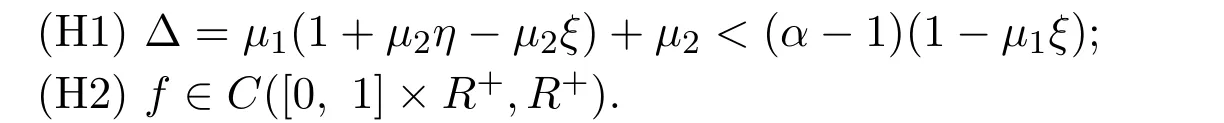
Due to the development of the theory of fractional calculus and its applications,such as in the fields of physics,electro-dynamics of complex medium,control theory,Bode’s analysis of feedback amplifiers,blood flow phenomena,aerodynamics and polymer rheology,electron-analytical chemistry,etc,many works on fractional calculus,fractional order differential equations have appeared[1-7].Recently,there have been many results concerning the solutions and positive solutions for boundary value problems for nonlinear fractional differential equations,see[8-29]and references therein.

For example,Bai and L¨u[12]considered the following Dirichlet boundary value problem of fractional differential equation

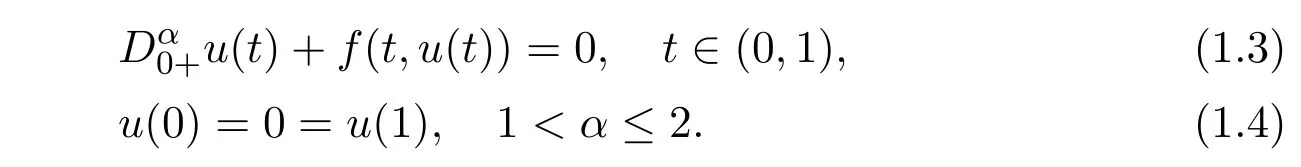
By means of different fixed-point theorems on a cone,some existence and multiplicity results of positive solutions were obtained.Jiang and Yuan[20]improved the results in[12]by discussing some new positive properties of the Green function for problem(1.3).By using the fixed point theorem on a cone due to Krasnoselskii,the authors established the existence results of positive solution for problem(1.3).Recently,Caballero et al.[21]obtained the existence and uniqueness of positive solution for singular boundary value problem(1.3).The existence results were established in the case that the nonlinear term f may be singular at t=0.

There are also some results concerning multi-point boundary value problems for differential equations of fractional order.

Wang et al.[25]considered the boundary value problem of fractional differential equation with integral condition

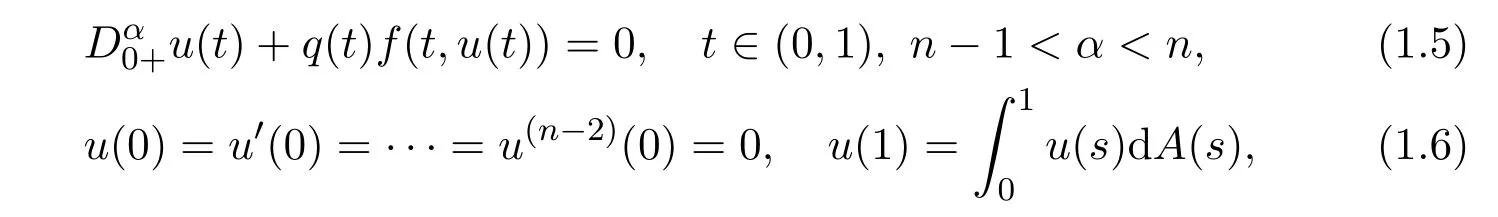
Many works deal with the existence and multiplicity of positive solution for fractional differential equation(1.1)under the boundary conditions(1.2).Zhao,Chai and Ge[28]considered a class of four-point fractional boundary value problem of the form

where 1＜α≤2,0≤ξ≤η≤1,0≤µ1,µ2≤1 with the condition

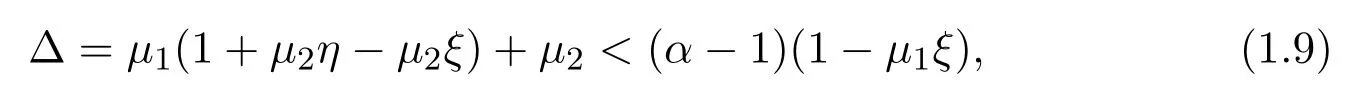
and f:[0,1]×R+→ R+is continuous.By using fixed-point theorems and successive iteration method,the authors established the existence results of at least one positive solution for this problem.

Yang and Zhang[29]considered the positive solution for the following boundary value problem of differential equation involving the Caputo’s fractional order derivative

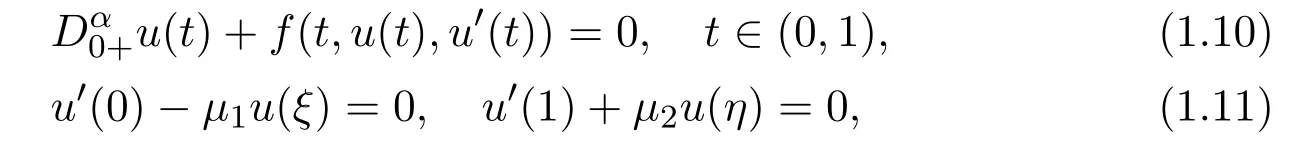
where 1＜α≤2,0≤ξ≤η≤1,0≤µ1,µ2≤1.By using the Avery-Peterson fixed point theorem,the existence of at least three positive solutions were established.

To complement the work on the positive solutions of problem(1.1)with(1.2),in this paper we consider the nonexistence of positive solution for problem(1.1)with(1.2).Sufficient conditions on the nonlinear term f and the explicit ranges of parameter λ,under which problem(1.1)with(1.2)has no positive solution,are given in Section 3.Some examples are presented in Section 4 to illustrate the main results.

2 Preliminary Results

Definition 2.1The Riemann-Liouville fractional integral of order α＞0 of a function u:(0,∞)→ R is given by

provided the right side is point-wise defined on(0,∞).

Definition 2.2The Caputo’s fractional derivative of order α ＞ 0 of a continuous function u:(0,∞)→ R is given by

where n−1＜α≤n,provided that the right side is point-wise defined on(0,∞).

Lemma 2.1Let α＞0.Then

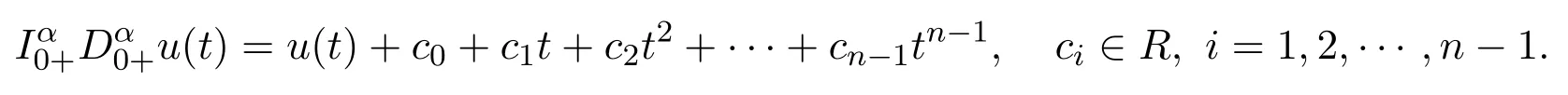
3 Main Results

Lemma 3.1[28]Given y(t)∈C[0,1].Then following FBVPs

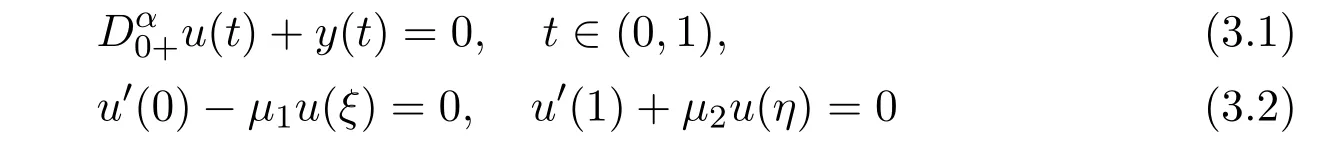
is equivalent to an operator equation

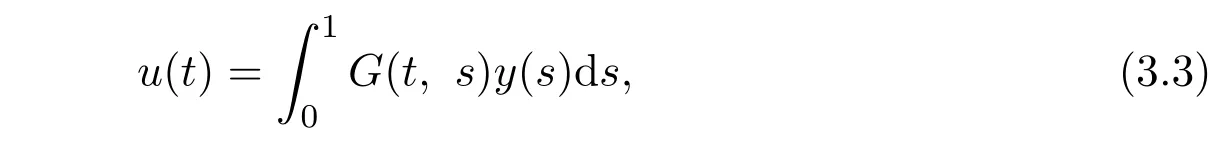
where

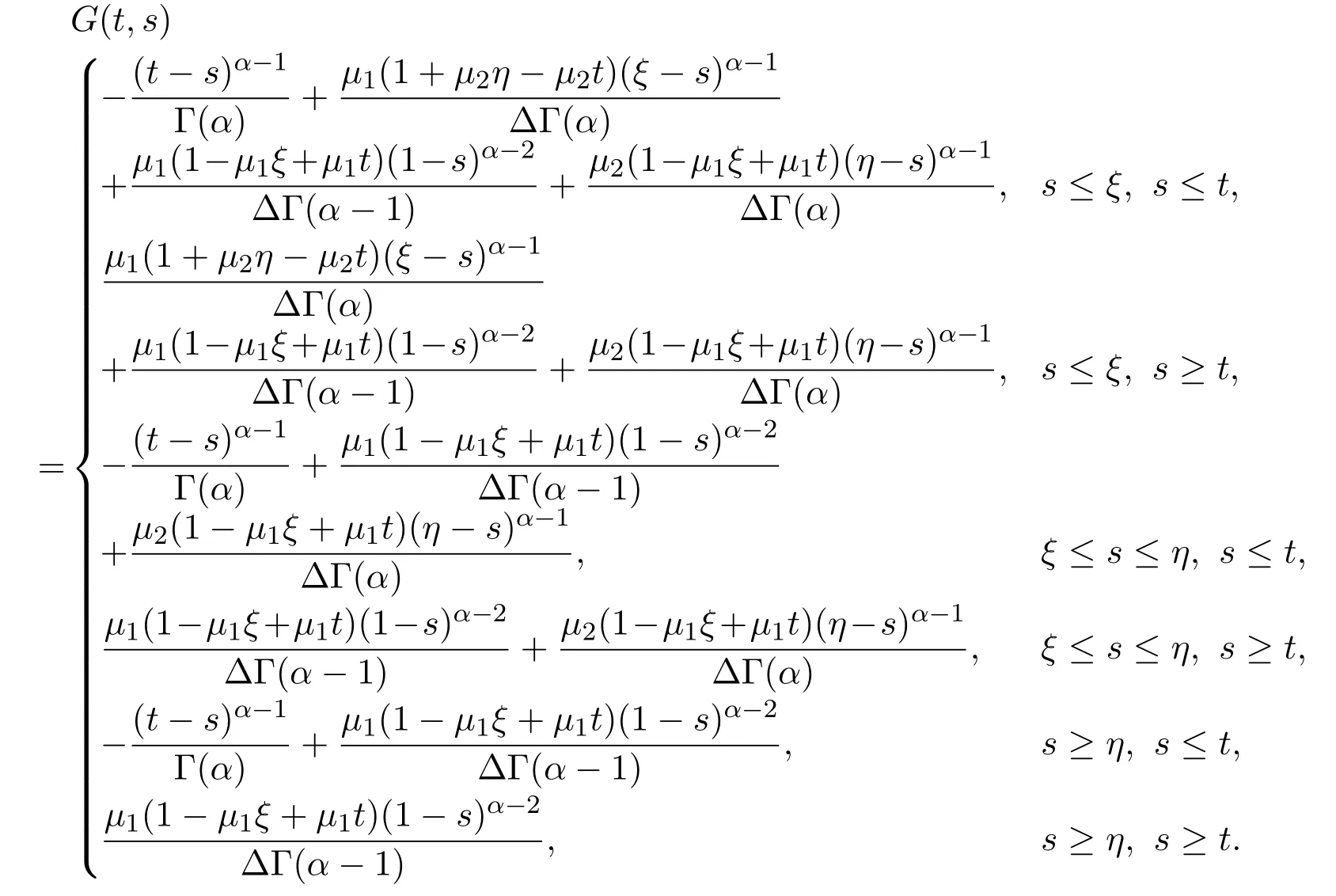
Lemma 3.2[28]Let G(t,s)be given as in the statement of Lemma 3.1.Then we find that

(1)G(t,s)is a continuous function on the unit square[0,1]×[0,1];

(2)G(t,s)≥0 for each(t,s)∈[0,1]×[0,1];

(3)G(t,s)≤ M(1−s)α−2,s∈ (0,1);

(4)there is a positive constant γ0∈ (0,1)such that

where

Here we introduce the following extreme limits:

Let the Banach space E=C[0,1]be endowed with the norm

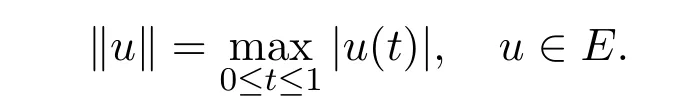
We define a cone K⊂E by

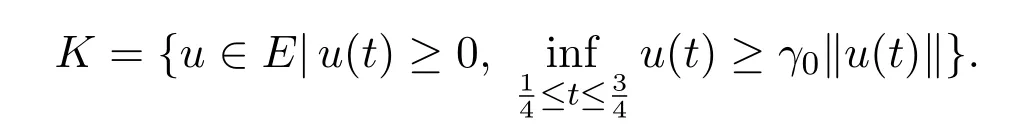
Lemma 3.3Let T:K→E be an operator defined by

Then T:K→K is completely continuous.

ProofThe operator T:K→E is continuous in view of the continuity of the functions G(t,s)and f(t,u(t),u′(t)).Let Ω ⊂ K be bounded.Then there exists a positive constant R1＞0 such that‖u‖≤R1,u∈Ω.

Denote

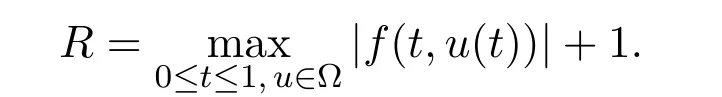
Then for u∈Ω,we have

Hence T(Ω)is bounded.For u∈ Ω,t1,t2∈ [0,1],one has

Thus,

By means of the Arzela-Ascoli theorem,we claim that T is completely continuous.Finally,we see that

Thus,we show that T:K→K is a completely continuous operator.

Theorem 3.1If,＜∞,then there exists a positive constant λ0such that for every λ ∈ (0,λ0),the boundary value problem(1.1)with(1.2)has no positive solution.

ProofFrom the definitions of,and the condition,＜∞,there exists an M1＞0 such that

De fine a positive constant

Let λ ∈ (0,λ0),then we suppose that problem(1.1)with(1.2)has a positive solution u(t),t∈[0,1].Thus,

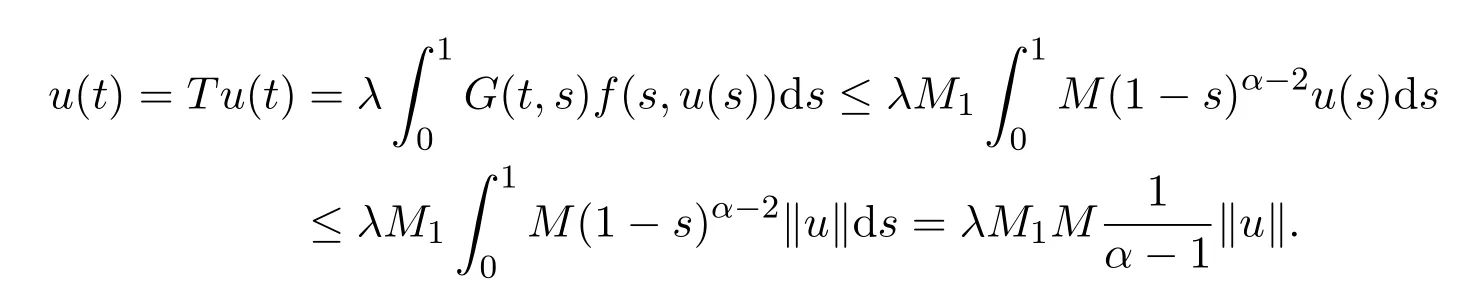
Therefore,

which is a contradiction.So the boundary value problem(1.1)with(1.2)has no positive solution.

Theorem 3.2If,＞0,then there exists a positive constantsuch that for every λ ＞,the boundary value problem(1.1)with(1.2)has no positive solution.

ProofFrom the definitions ofand,there exists a positive number m1such that

Define a positive constant

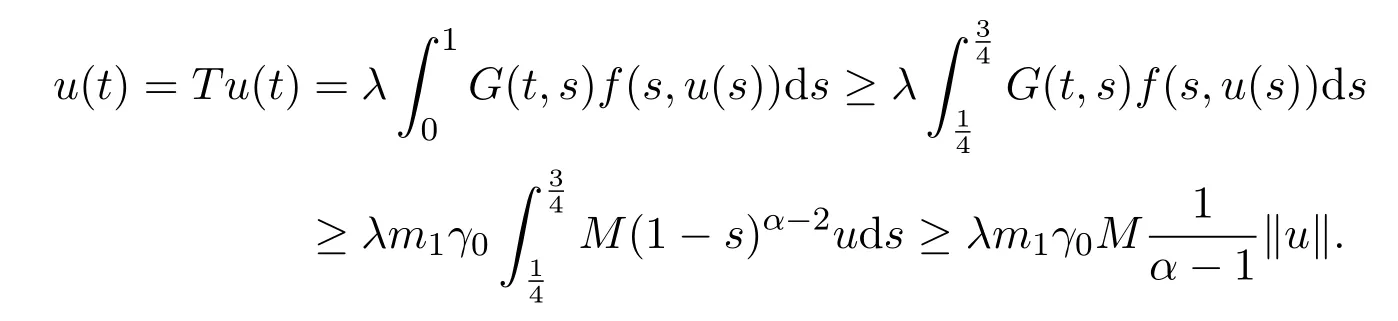
Thus,

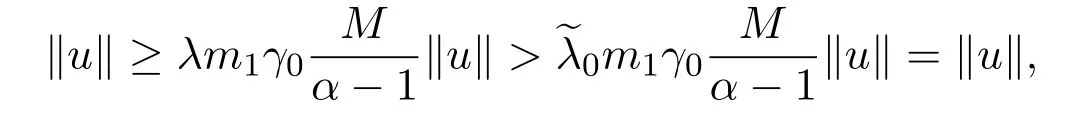
which is a contradiction.So the boundary value problem(1.1)with(1.2)has no positive solution.

4 Example

Consider a nonlinear FBVPs

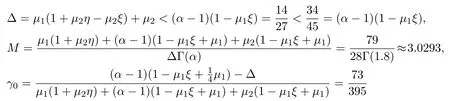
and

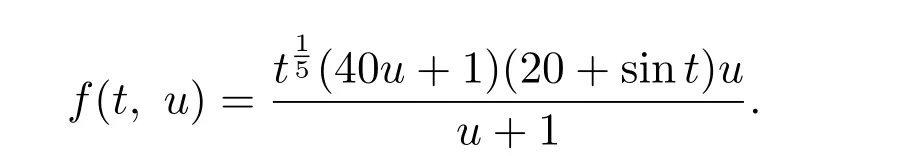
By simple computation,we have

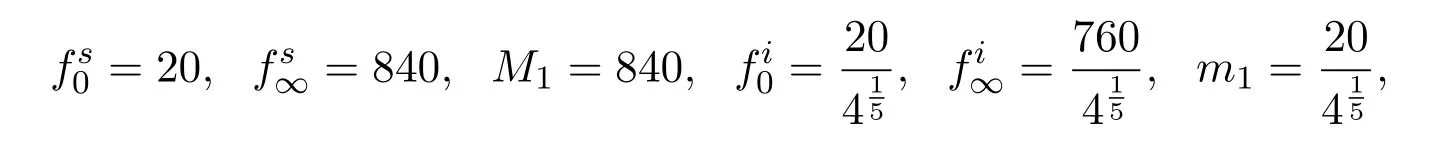
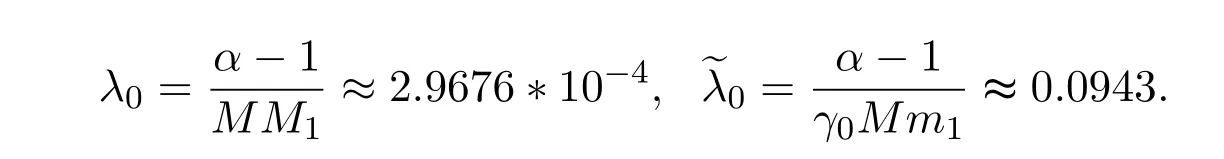
From Theorem 3.1,for every λ ∈ (0,λ0),problem(4.1)with(4.2)has no positive solution.From Theorem 3.2,for every λ＞,problem(4.1)with(4.2)has no positive solution.

[1]D.Delbosco,Fractional calculus and function spaces,J.Fract.Calc.,6(1994),45-53.

[2]K.S.Miller,B.Ross,An Introduction to the Fractional Calculus and Fractional Differential Equations,Wiley,New York,1993.

[3]V.Lakshmikantham,S.Leela,Theory of fractional differential inequalities and applications,Com.Appl.Anal.,11(2007),395-402.

[4]V.Lakshmikantham,J.Devi,Theory of fractional differential equations in a Banach space,European J.Pure.Appl.Math.,1(2008),38-45.

[5]V.Lakshmikantham,S.Leela,Nagumo-type uniqueness result for fractional differential equations,Nonlinear Anal.TMA,71(2009),2886-2889.

[6]V.Lakshmikantham,S.Leela,A Krasnoselskii-Krein-type uniqueness result for fractional differential equations,Nonlinear Anal.TMA,71(2009),3421-3424.

[7]V.Lakshmikantham,Theory of fractional differential equations,Nonlinear Anal.TMA,69(2008),3337-3343.

[8]C.Yu,G.Gao,Existence of fractional differential equations,J.Math.Anal.Appl.,310(2005),26-29.

[9]S.Zhang,The existence of a positive solution for a nonlinear fractional differential equation,J.Math.Anal.Appl.,252(2000),804-812.

[10]S.Zhang,Existence of positive solution for some class of nonlinear fractional differential equation,J.Math.Anal.Appl.,278(2003),136-148.

[11]A.Babakhani,V.D.Gejji,Existence and positive solutions of nonlinear Fractional differential equations,J.Math.Anal.Appl.,278(2003),434-442.

[12]Z.Bai,H.L¨u,Positive solutions for boundary value problem of nonlinear fractional differential equation,J.Math.Anal.Appl.,311(2005),495-505.

[13]N.Kosmatov,A singular boundary value problem for nonlinear differential equations of fractional order,J.Appl.Math.Comput.,29(2009),125-135.

[14]X.J.Xu,D.Q.Jiang,C.J.Yuan,Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equations,Nonlinear Anal.TMA,71(2009),4676-4688.

[15]X.Su,Boundary value problem for a coupled system of nonlinear fractional differential equations,Appl.Math.Lett.,22(2009),64-69.

[16]S.Liang,J.Zhang,Positive solutions for boundary value problems of nonlinear fractional differential equation,Nonlinear Analysis,71(2009),5545-5550.

[17]R.P.Agarwal,et at.,Positive solutions for Dirichlet problems of singular nonlinear fractional differential equations,J.Math.Anal.Appl.,371(2010),57-68.

[18]C.Goodrich,Existence of a positive solution to a class of fractional differential equations,Appl.Math.Lett.,23(2010),1050-1055.

[19]D.Jiang,C.Yuan,The positive properties of the Green function for Direchlet-type boundary value problems of nonlinear fractional differential equations and its application,Nonlinear Anal.,15(2010),710-719.

[20]J.Caballero,J.Harjani,K.Sadarangani,Positive solutions for a class of singular fractional boundary value problems,Comput.Math.Anal.,62(2011),1325-1332.

[21]B.Ahmad,J.Nieto,Existence results for a coupled system of nonlinear fractional differential equations with three-point boundary conditions,Comput.Math.Appl.,58(2009),1838-1843.

[22]Z.Bai,On positive solutions of a nonlocal fractional boundary value problem,Nonlinear Anal.TMA,72(2010),916-924.

[23]B.Ahmad,S.Sivasundaram,On four-point nonlocal boundary value problems of nonlinear integro-differential equations of fractional order,Appl.Math.Comput.,217(2010),480-487.

[24]C.Li,X.Luo,Y.Zhou,Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations,Comput.Math.Appl.,59(2010),1363-1375.

[25]Y.Wang,L.Liu,Y.Wu,Positive solutions for a nonlocal fractional differential equation,Nonlinear Anal.,74(2011),3599-3605.

[26]H.Salem,On the fractional calculus in abstract spaces and their applications to the Dirichlet-type problem of fractional order,Comput.Math.Appl.,59(2010),1278-1293.

[27]M.Rehman,R.Khan,Existence and uniqueness of solutions for multi-point boundary value problems for fractional differential equations,Appl.Math.Lett.,23(2010),1038-1044.

[28]X.K.Zhao,C.W.Chai and W.G.Ge,Positive solutions for fractional four-point boundary value problems,Commun.Nonlinear Sci.Numer.Simulat.,16(2011),3665-3672.

[29]L.Yang,W.Zhang,Application of Avery-Peterson fixed point theorem to nonlinear boundary value problem of fractional differential equation with the Caputo’s derivative,Commun.Nonlinear Sci.Numer.Simulat.,17(2012),4576-4584.