POSITIVE PERIODIC SOLUTIONS OF THE FIRSTORDER SINGULAR DISCRETE SYSTEMS∗†

Ruipeng Chen,Xiaoya Li

(Dept.of Math.,North Minzu University,Yinchuan 750021,Ningxia,PR China)

1 Introduction

Let T＞3 be an integer.In this paper,we are concerned with the existence and multiplicity of positive T-periodic solutions of the following singular discrete systems

and

where u=(u1,···,un)∈ Rn,ai,bi:Z → [0,∞)are T-periodic functions with

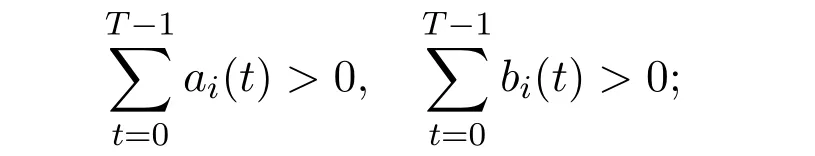
gi∈ C(,[0,∞))and fi:{0} → [0,∞)are continuous,i=1,2,···,n; τ:Z → Z is a T-periodic function and λ is a positive parameter.

In the past few years,there has been considerable interest in the existence of periodic solutions of equations

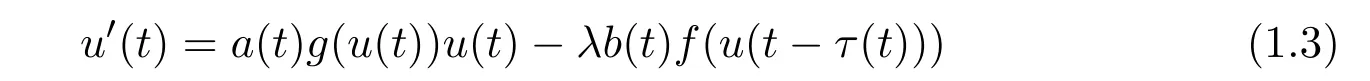
and

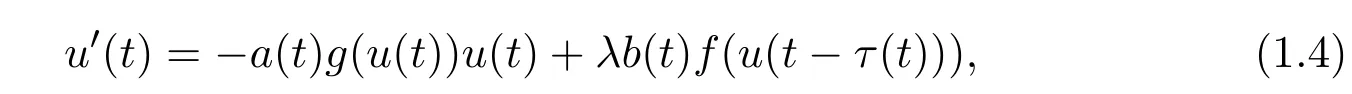
where a,b∈ C(R,[0,∞))are T-periodic functions with

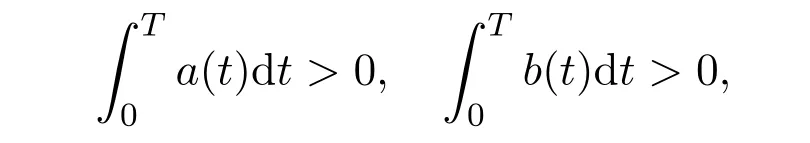
and τ is a continuous T-periodic function.Equations(1.3)and(1.4)have been proposed as models for a variety of physiological processes and conditions including production of blood cells,respiration,and cardiac arrhythmias.See for example,[1-8,12]and the references therein.On the other hand,many authors paid their attention to the existence of positive periodic solutions of singular systems of the first-order and second-order differential equations,see Chu[9],Jiang[10],Wang[11,12]and the references therein.It has been shown that many results of nonsingular systems still valid for singular cases.

Let

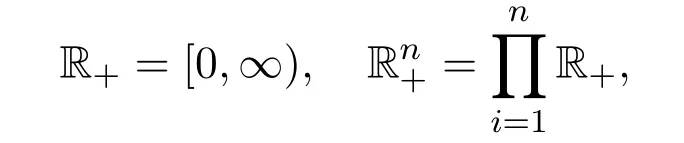
and for any u=(u1,···,un)∈,

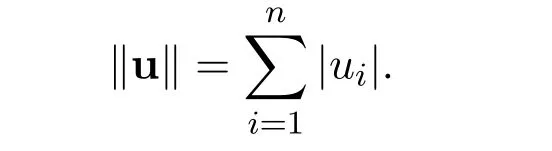
Recently,Wang[12]studied the existence and multiplicity of positive periodic solutions of the following singular non-autonomous n-dimensional system

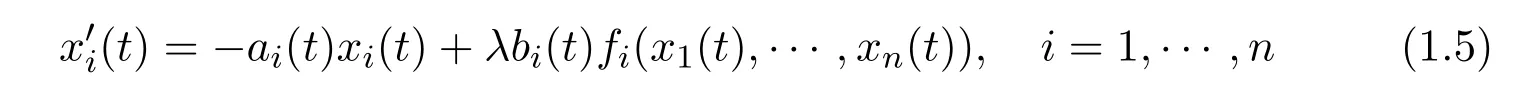
under assumptions

(H1)ai,bi∈ C(R,[0,∞))are ω-periodic functions such that

(H2)fi:{0} → (0,∞)are continuous,i=1,···,n.

By using Krasnoselskii fixed point theorem in a cone,the author established the existence and multiplicity of positive periodic solutions of(1.5)with superlinearity or sublinearity assumptions at infinity for an appropriately chosen parameter.

However,to the best of our knowledge,the existence results of positive periodic solutions for first-order discrete systems(1.1)and(1.2)with singular nonlinearities are relatively little.Motivated by the above considerations,in this paper,we study the existence and multiplicity of positive T-periodic solutions of singular discrete systems(1.1)and(1.2).Obviously,(1.1)is a discrete analogue of system(1.5)when gi≡ 1,i=1,2,···,n and τ≡ 0,and we are interested in establishing the similar results as[12,Theorem 1.1]for systems(1.1)and(1.2).

We make the following assumptions:

(C1)ai,bi:Z→[0,∞)are T-periodic functions withi=1,2,···,n;τ:Z → Z is a T-periodic function.

(C2)gi∈C(,[0,∞))satisfies 0＜li≤gi(u)≤Li＜∞,fi:{0}→(0,∞)is continuous,i=1,2,···,n.

(C3)0 ≤ liai(t)≤ Liai(t)＜ 1,t∈ T:={0,1,···,T −1},i=1,2,···,n.

Our main results can be stated as below.

Theorem 1.1Let(C1)-(C3)hold.Suppose= ∞ f or some i=1,2,···,n,then:

(iii)There exists a λ0＞ 0 such that(1.1)admits a positive periodic solution for 0＜λ＜λ0.

Remark 1.1Theorem 1.1,which improves the corresponding ones established for single difference equations in[17-21],is the discrete analogues of[12,Theorem 1.1]when gi≡ 1,i=1,2,···,n and τ≡ 0.For more details on the periodic solutions of systems(1.1)and(1.2),we refer the readers to[13-16].

The following well-known theorem plays a key role in proving our main results.

Theorem A[22,23]Let E be a Banach space and P be a cone in E.For r＞0,define Pr={u ∈ P :‖u‖ ＜ r }.Assume T:→P is completely continuous such that Tu≠u for u ∈ ∂Pr={u ∈ P:‖u‖ =r}.

(i)If ‖Tu‖＞ ‖u‖ for u ∈ ∂Pr,then i(T,Pr,P)=0.

(ii)If ‖Tu‖＜ ‖u‖ for u∈ ∂Pr,then i(T,Pr,P)=1.

2 Preliminaries

Set

For r＞0,de fine

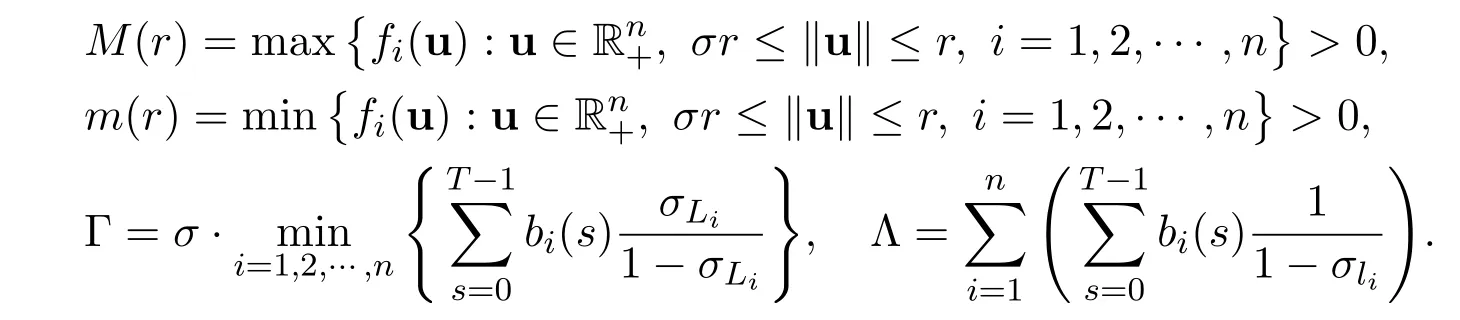
Let E={u:Z→R|u(t+T)=u(t),t∈Z}be a Banach space with the normand X be a Banach space defined by

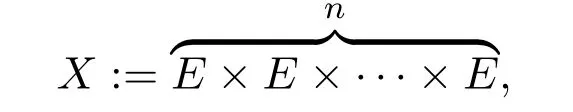
which is equipped with the norm

Define

It is not difficult to check that K is a cone in X.For r＞ 0,let

then ∂Ωr={u ∈ K:‖u‖=r}.

Let Tλ:X→X be a mapping with components(,···,):

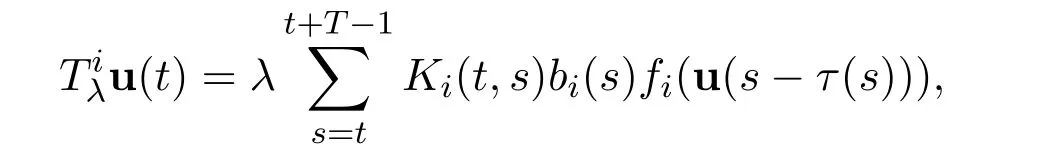
where

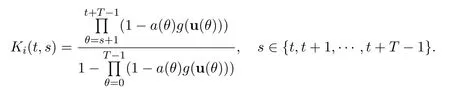
It follows from(C3)that

Moreover,we can easily get

Lemma 2.1Let(C1)-(C3)hold.Then Tλ(K)⊂K and Tλ:K→K is compact and continuous.

ProofIn view of the definition of K,for u ∈ K and i=1,2,···,n,

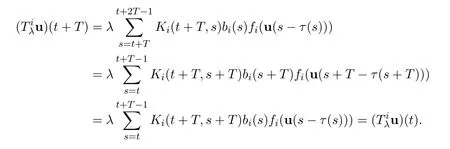
Indeed,since aiis T-periodic and u∈K,we get

and thus Tλu∈X.One can show that,for u∈K and t∈T,

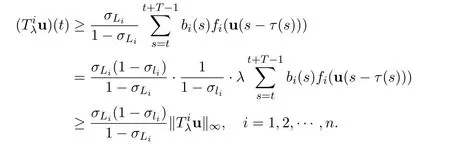
Therefore Tλ(K)⊂ K and Tλ:K → K is compact and continuous.The proof is completed.

Using the similar methods as in the proof of[12,Lemma 2.2]with obvious changes,we can obtain the following lemma.

Lemma 2.2Let(C1)-(C3)hold.Then u∈K{0}is a positive periodic solution of system(1.1)if and only if u is a fixed point of Tλin K{0}.

Lemma 2.3Let(C1)-(C3)hold.For any η＞0 and u∈K{0},if there exists a fisuch thatfor t∈ T ,then ‖Tλu‖ ≥ λ Γη‖u‖.

ProofSince u∈K{0}andfor t∈ T ,we have

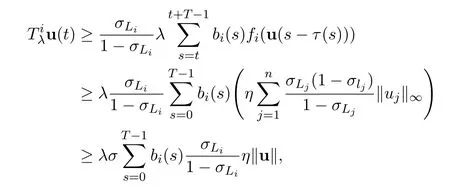
which implies‖Tλu‖≥ λΓη‖u‖.The proof is completed.

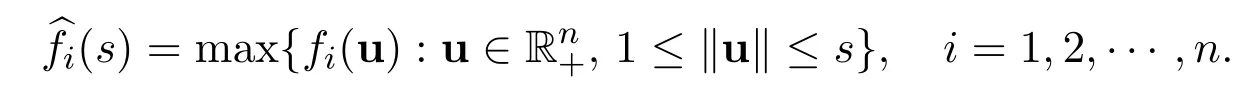
Lemma 2.4[11,12]exists(which can be infinity),thenexists and

Lemma 2.5Suppose(C1)-(C3)hold and r＞.If there exists an ε＞ 0 such that(r)≤ εr,i=1,2,···,n,then ‖Tλu‖≤ λεΛ‖u‖ for u ∈ ∂Ωr.

ProofFor u∈∂Ωr,we have

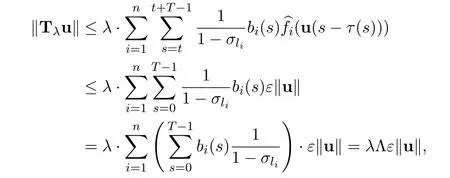
and the proof is completed.

When u∈∂Ωr,r＞0,the definitions of M(r)and m(r)yield

Thus by the similar manners as in the proof of Lemmas 2.3 and 2.5,we can easily obtain the following lemmas.

Lemma 2.6Let(C1)-(C3)hold.If u ∈ ∂ Ωrand r＞ 0 ,then‖Tλu‖ ≥m(r).

Lemma 2.7Let(C1)-(C3)hold.If u∈∂Ωrand r＞0,then‖Tλu‖≤ λΛM(r).

3 Proof of Theorem 1.1

(i)It follows from the assumption that there exists an r1＞0 such that

Lemma 2.3 implies‖Tλu‖≥ λΓη‖u‖＞ ‖u‖,for u ∈ ∂Ωr1.

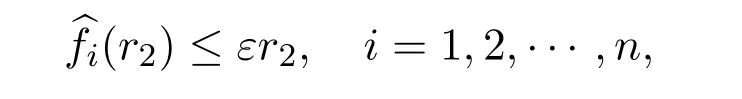
where ε＞ 0 satisfies λΛε＜ 1.And then by Lemma 2.5,we get

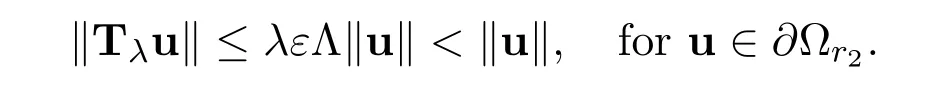
It follows from Theorem A that

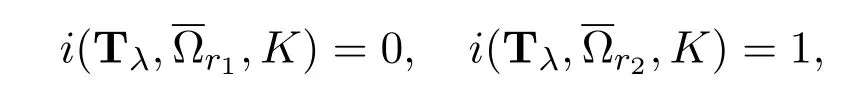
consequently i(Tλ,Ωr1,K)=1.Hence,Tλhas a fixed point u inΩr1,which is just a positive periodic solution of system(1.1).

(ii)Let r1＞ 0 be fixed.By Lemma 2.7,there exists a λ0＞ 0 such that

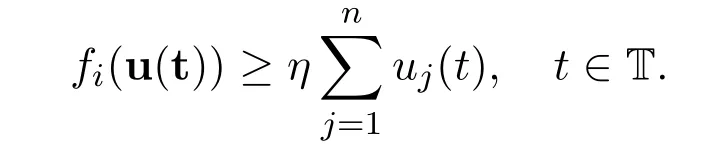
Lemma 2.3 implies‖Tλu‖≥ λΓη‖u‖＞ ‖u‖,for u ∈ ∂Ωr2.

3

which yields

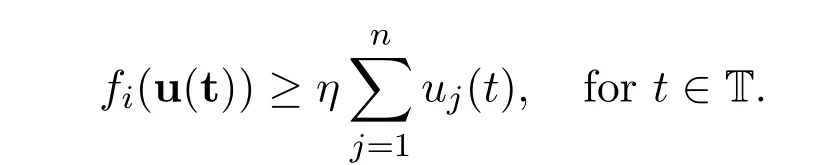
And then Lemma 2.3 shows

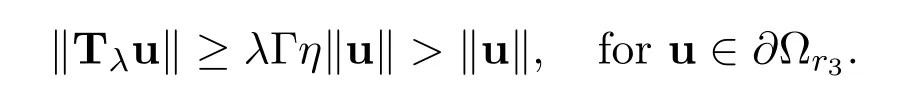
By Theorem A,we can easily obtain

consequently

Hence Tλhas two fixed points lying inwhich are positive periodic solutions of(1.1).

(iii)For a fixed number r1＞ 0,Lemma 2.7 implies there exists a λ0＞ 0 such that

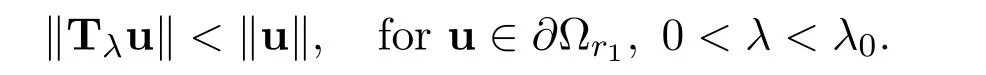
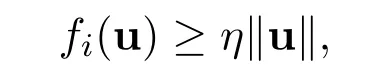
It follows from Lemma 2.3 that‖Tλu‖≥ λΓη‖u‖＞ ‖u‖,for u ∈ ∂Ωr2.

Using Theorem A again,we can get

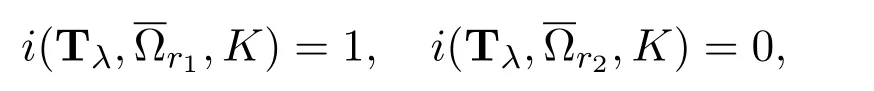
so i(Tλ,Ωr2,K)=1.Hence,Tλhas a fixed point u inΩr1Ωr2for 0＜ λ ＜ λ0,which is a positive periodic solution of system(1.1).The proof is completed.

4 Positive Periodic Solutions of System(1.2)

In this Section,we shall establish the existence and multiplicity of positive T-periodic solutions of singular discrete system(1.2),that is,

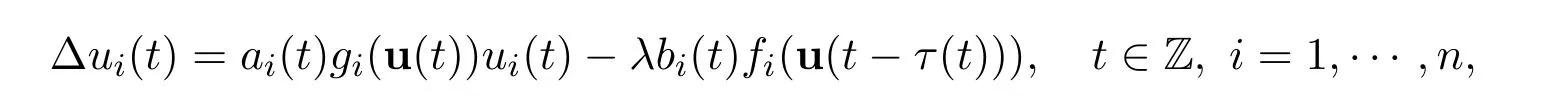
where λ, τ,ai,bi,fi(u),gi(u)satisfy the same assumptions stated for system(1.1).In view of(1.2),we can de fine an operator Tλ:X →X with components(,···,):

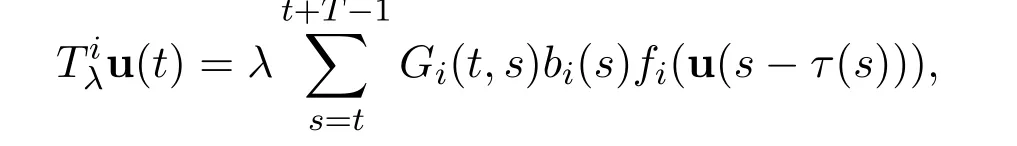
where

Clearly,(C1)and(C2)imply for all t∈ T and i=1,2,···,n,

De fine a cone in X by

By the similar arguments as in Sections 2 and 3,we can establish the following theorems.

Theorem 4.1Let(C1)and(C2)hold.Assume= ∞ f or some i=1,2,···,n.

(iii)There exists a λ0＞ 0 such that(1.2)admits a positive periodic solution for 0＜λ＜λ0.

Finally,consider discrete systems(1.1)and(1.2)without singularities,that is,we replace(C2)with the following condition.

Then the following two theorems can be established by the similar methods adopted in Sections 2 and 3.

Theorem 4.2Let(C1),()and(C3)hold.Assume=0 for i=1,2,···,n.

(iii)There exists a λ0＞ 0 such that(1.1)admits a positive periodic solution for λ＞λ0.

Theorem 4.3Let(C1)and()hold.Assume=0 for i=1,2,···,n.

(iii)There exists a λ0＞ 0 such that(1.2)admits a positive periodic solution for λ＞λ0.

Remark 4.1Note that Theorems 4.1-4.3 enrich and complement Theorem 1.1.And obviously,Lemma 2.6 is crucial to prove Theorems 4.2-4.3.

[1]W.S.Gurney,S.P.Blythe,R.N.Nisbet,Nicholson’s blow flies revisited,Nature,287(1980),17-21.

[2]M.C.Mackey,L.Glass,Oscillations and chaos in physiological control systems,Science,197(1997),287-289.

[3]M.Wazewska-Czyzewska,A.Lasota,Mathematical problems of the dynamics of a system of red blood cells,Mat.Stosow,6(1976),23-40.(in Polish)

[4]Y.Kuang,Delay Differential Equations with Applications in Population Dynamics,Academic Press,New York,1993.

[5]H.I.Freedman,J.Wu,Periodic solutions of single-species models with periodic delay,SIAM J.Math.Anal.,23(1992),689-701.

[6]S.N.Chow,Existence of periodic solutions of autonomous functional differential equations,J.Differential Equations,15(1974),350-378.

[7]Z.Jin,H.Wang,A note on positive periodic solutions of delayed differential equations,Appl.Math.Lett.,23:5(2010),581-584.

[8]R.Ma,R.Chen,T.Chen,Existence of positive periodic solutions of nonlinear firstorder delayed differential equations,J.Math.Anal.Appl.,384(2011),527-535.

[9]J.Chu,P.J.Torres,M.Zhang,Periodic solutions of second order non-autonomous singular dynamical systems,J.Differential Equations,239(2007),196-212.

[10]D.Jiang,J.Chu,D.O’Regan,R.P.Agarwal,Multiple positive solutions to superlinear periodic boundary value problems with repulsive singular forces,J.Math.Anal.Appl.,286(2003),563-576.

[11]H.Wang,Positive periodic solutions of singular systems with a parameter,J.Differential Equations,249(2010),2986-3002.

[12]H.Wang,Positive periodic solutions of singular systems of first order ordinary differential equations,Appl.Math.Comput.,218(2011),1605-1610.

[13]Y.Chen,Z.Zhou,Stable periodic solution of a discrete periodic Lotka-Volterra competition system,J.Math.Anal.Appl.,277(2003),358-366.

[14]A.Cabada,Victoria Otero-Espinar,Dolores R.Vivero,Optimal conditions to ensure the stability of periodic solutions of first order difference equations lying between lower and upper solutions,J.Comput.Appl.Math.,176(2005),45-57.

[15]Y.Li,L.Zhu,Existence of positive periodic solution for difference equations with feedback control,Appl.Math.Lett.,18(2005),61-67.

[16]R.P.Agarwal,W.Li,P.Y.H.Pang,Asymptotic behavior of nonlinear difference systems,Appl.Math.Comput.,140(2003),307-316.

[17]Y.N.Raffoul,Positive periodic solutions of nonlinear functional difference equations,Electron.J.Differential Equations,2002:55(2002),1-8.

[18]Y.Li,L.Zhu,P.Liu,Positive periodic solutions of nonlinear functional difference equations depending on a parameter,Comput.Math.Appl.,48(2004),1453-1459.

[19]M.Ma,J.Yu,Existence of multiple positive periodic solutions for nonlinear functional difference equations,J.Math.Anal.Appl.,305(2005),483-490.

[20]R.Ma,C.Gao,J.Xu,Existence of positive solutions for first order discrete periodic boundary value problems with delay,Nonlinear Analysis:TMA,74(2011),4186-4191.

[21]R.Ma,T.Chen,Y.Lu,Positive periodic solutions of nonlinear first-order functional difference equations,Discrete Dynamics in Nature and Society,2010(2010),Article ID 419536,15 pages,doi:10.1155/2010/419536.

[22]K.Deimling,Nonlinear Functional Analysis,Springer,Berlin,1985.

[23]D.Guo,V.Lakshmikantham,Nonlinear Problems in Abstract Cones,Academic Press,Orlando,FL,1988.