THE SYMMETRY DESCRIPTION OF A CLASS OF FRACTIONAL STURM-LIOUVILLE OPERATOR∗†

Shouyi Li,Zhaowen Zheng

(School of Mathematical Science,Qufu Normal University,Qufu 273165,Shandong,PR China)

1 Introduction

Recently,fractional differential equations have drawn much attention.It is caused both by the theory of fractional calculus itself and by the applications in various fields of science and engineering such as control,electrochemistry,electromagnetic,porous media,viscoelasticity,etc,for detail,see[1-5].

In this paper,we consider the following fractional Sturm-Liouville operator:

acting on the Hilbert space L2[0,1]with the following boundary condition:

where p(x)≠0,p(x)∈C1(0,1),q(x)∈C(0,1),0＜α＜1 and aij,bij∈R(i,j=1,2).,andare fractional integral operator,fractional derivative and Caputo fractional derivator acting on given functions respectively.Our purpose is to find sufficient conditions on the coefficients matrices A and B to guarantee a symmetric operator,where

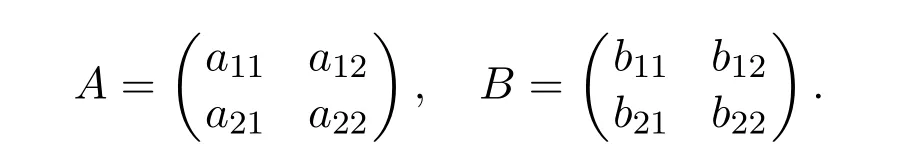
We know that,the second-order Sturm-Liouville differential expression

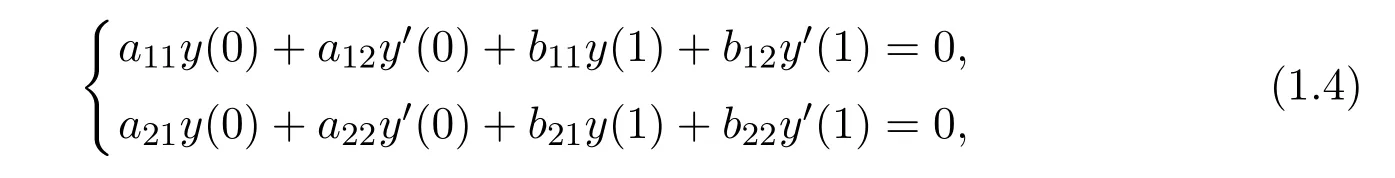
when the coefficient matrices satisfy

generates a self-adjoint operator,where

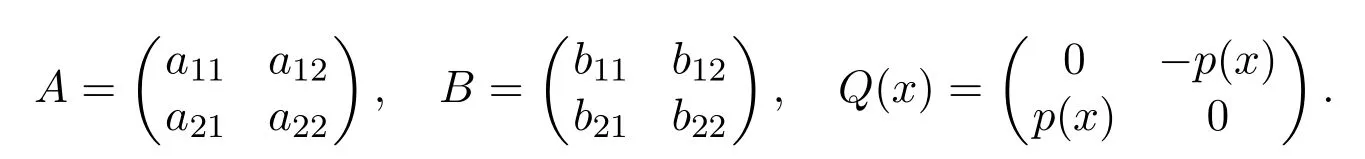
This result has great significance in the spectral theory of Sturm-Liouville operator.

A nature thought is to imitate the second-order Sturm-Liouville problem,and thereby the self-adjoined description of the fractional Sturm-Liouville problem is given.However,a fractional derivation operator is quite different from an ordinary differential operator in some properties,especially we fail to get the existence and uniqueness of the fractional equation till now.Therefore,the method can not be completely applied to study our problem.

2 Preliminaries

We will use the following properties of fractional integrals and derivatives.

Definition 2.1[3]For given α with R(α) ＞ 0,the left and right Riemann-Liouville integrals of order α are defined as

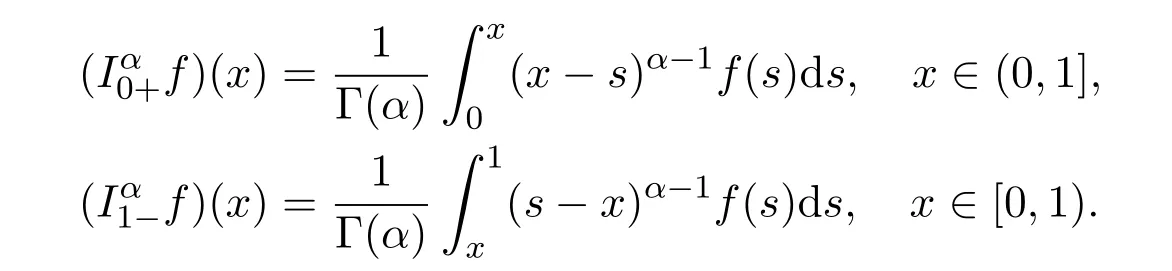
Definition 2.2[3]Let R(α)∈ (n−1,n),where n ∈ N,D=.The left and right Riemann-Liouville derivatives of order α are de fined as

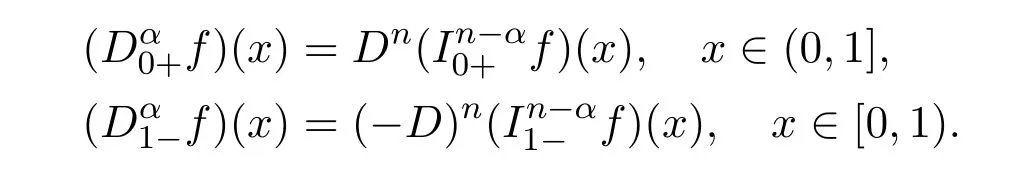
In particular,when 0＜α＜1,we have

Definition 2.3[3]Let R(α)∈ (n−1,n),where n ∈ N,D=.The left and right Caputo derivatives of order α are de fined as

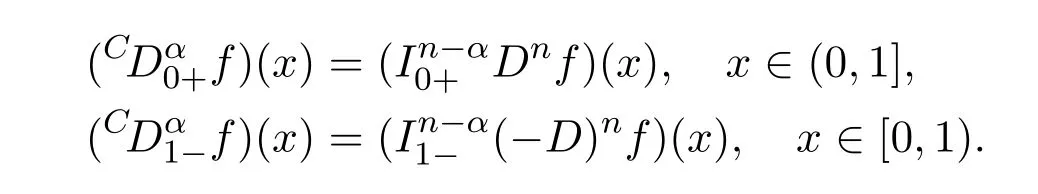
In particular,when 0＜α＜1,we have

Lemma 2.1[3]Let R(α)∈ (n−1,n),where n∈ N.If y∈ ACn[0,1],then the fractional derivativesandexist almost everywhere on[0,1]and can be represented in forms

Lemma 2.2[3]Let α ∈(n−1,n),where n∈N.Then operators,,andsatisfy the following integrations by parts,

Lemma 2.3[3]Fractional integration operatorsandwith R(α)≥0 are bounded in Lp(0,1)(1≤p≤∞):

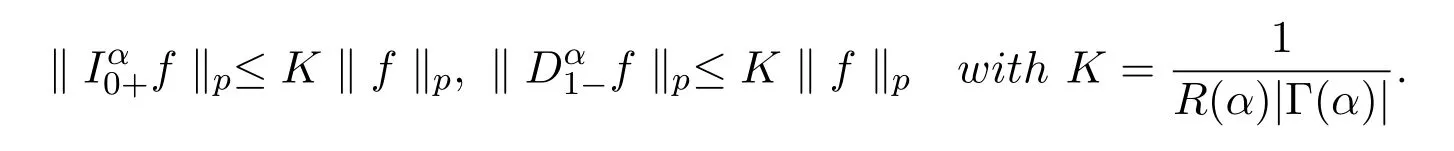
Corollary 2.1Fractional integration operatorsandare operators defined on Lp(0,1)(1≤p≤∞).

ProofFor all f∈Lp(0,1),it is easy to see that f satisfies

so

Therefore,the integral operatoris an operator from Lp(0,1)to Lp(0,1)(1≤p≤∞).

Lemma 2.4[3]If R(α)＞ 0 and f(x)∈ Lp(0,1)(1≤p≤ ∞),then the following equalities

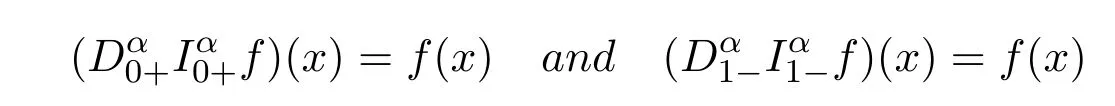
hold almost everywhere on[0,1].

Lemma 2.5[3]If α/∈N,then the Caputo fractional derivatives coincide with the Riemann-Liouville fractional derivatives in the following cases:

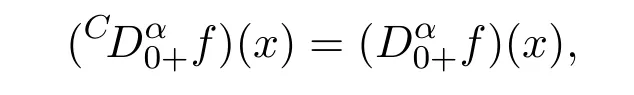
if

if

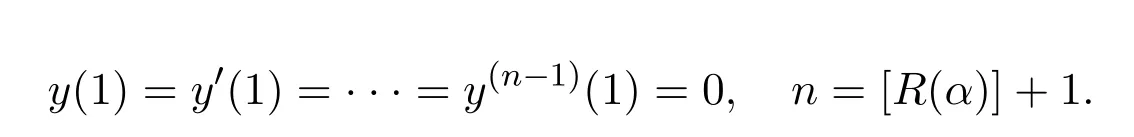
Lemma 2.6[3]The space ACn[0,1]consists of those and only those functions f(x)which can be represented in the form

where φ ∈ L(0,1),ck(k=0,1,···,n − 1)are arbitrary constants,and

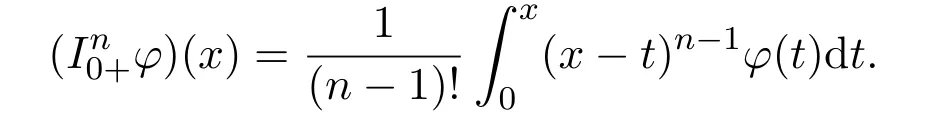
Consider the following fractional differential equation

Assume that p(x)≠0,p(x)∈C1(0,1)and q(x)∈C(0,1),obviously,l cannot act on the whole space L2[0,1].

Definition 2.4The subset of L2[0,1]which satisfies:

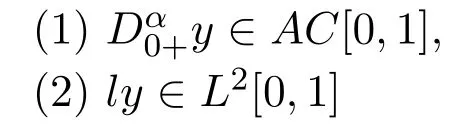
is called the maximal operator domain of l,denoted by DM.The operator generated by it is called maximal operator,denoted by LM.

Definition 2.5The subset of DMwhich satisfies:

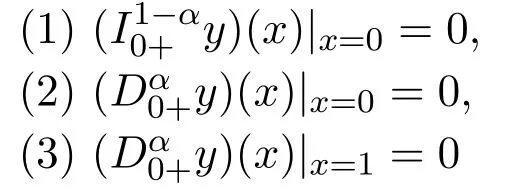
is called the minimal operator domain of l,denoted by Do.The operator generated by it is called minimal operator,denoted by Lo.

Let y and z be two functions of DM.Using Lemma 2.2,we obtain

and

So,

Denote

[yz](x)is called the lagrange bilinear form about l,and it is also called the fit function of y and z.We denote by=[yz](1)−[yz](0).Then we obtain

Denote

Then

Q(x)is called the fit matrix of l.

Definition 2.6Let y∈L2[0,1],the boundary type of y is defined as

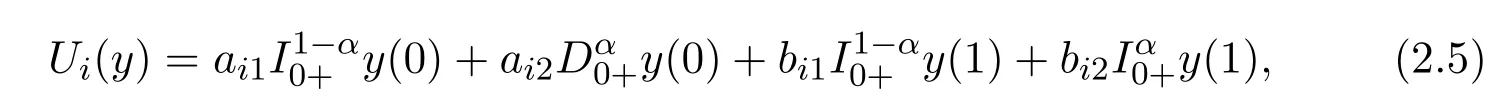
where aij,bij∈ C(i=1,2,···,r;1≤ r≤ 4).

Denote

So U(y)can be expressed in the following form

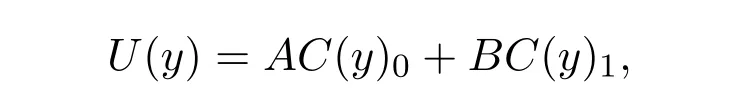
where C(y)0=C(y)|x=0,and C(y)1is defined in the same way.We call U(y)the boundary type vector.

Let

Moreover,

If rank(A⊕B)=r,U(y)is called of r-dimensional,or U1,···,Urare linearly independent.We always assume they are linearly independent in the following discussion.

For r=1,2,3,let Ur+1,···,U4be 4−r linearly independent boundary types,and their vector form is Ucy.If the boundary type vector

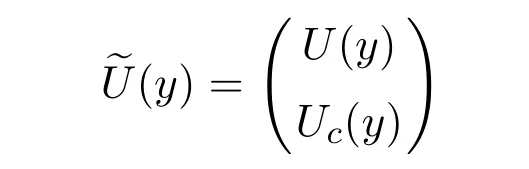
is 4-dimensional,we say that U(y)and Uc(y)are complementary.Apparently,it is possible to find complementary boundary type vector of any boundary type vector.

3 Main Results

Theorem 3.1For given r-dimensional boundary type vector U(y)and its complementary(4−r)-dimensional boundary type vector Uc(y),there is a unique r-dimensional Vc(z)and its(4−r)-dimensional boundary type vector V(z),which satisfy

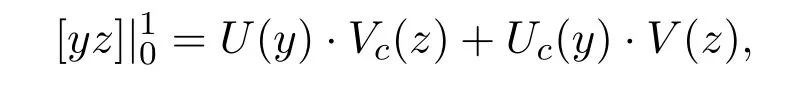
where “·” is the inner product of Euclidean space.

ProofLet

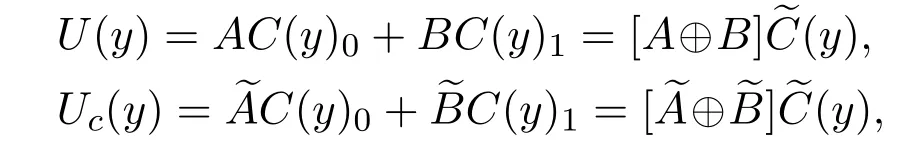
where A and B are(r×2)-dimensional matrices,andare(4−r)×2-dimensional matrices.

Let

Since U and Ucare complementary,H is a non-singular matrix,so we obtain

By(2.4),

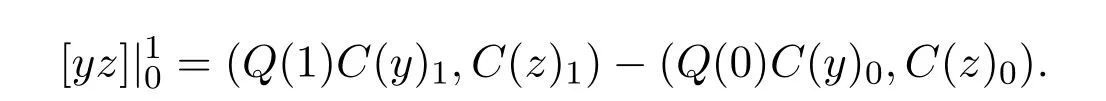
Let

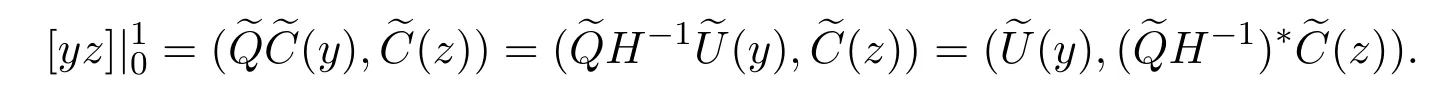
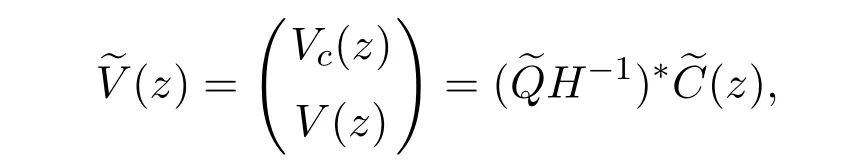
then it is a 4-dimensional boundary type vector,where Vc(z)is an r-dimensional boundary type vector,V(z)is its complementary(4−r)-dimensional boundary type vector.Since(z)is determined by H,

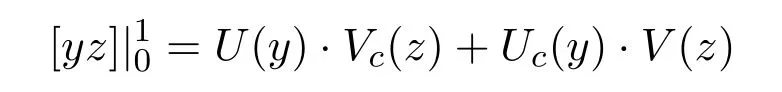
is determined by U and Uc.

Definition 3.1V(z)is called the adjoint boundary type vector of U(y),where V(z)and U(y)are defined as above.

If V(z)is an adjoint boundary type vector of U(y),then U(y)is an adjoint boundary type vector of V(y),and they are adjoint boundary type vectors of each other.

Definition 3.2If two boundary type vectors V(y)and V′(y)satisfy V′(y)=CV(y),where C is a non-singular matrix,then they are called equivalent;if a boundary type vector V(y)is equivalent with its adjoint boundary type vector,we call it is self-conjugate.

Obviously,a boundary type vector is self-conjugate,then its dimension r must satisfy r=4−r,that is r=2.

Definition 3.3If U(y)and V(z)are adjoint boundary type vectors of each other,we say that U(y)=0 and V(z)=0 are adjoint boundary conditions of each other;if U(y)is self-conjugate,we say that U(y)=0 is a self-conjugate boundary condition.

Definition 3.4Assume that H1and H2are Hilbert spaces,T is an operator from H1into H2,and S is an operator from H2into H1.The operator S is called a formal adjoint of T if we have

T is then a formal adjoint of S,too.

Theorem 3.2Let L and L′be operators generated by l(y).The domain of L is defined by the boundary condition U(y)=0,and the domain of L′is defined by the boundary condition V(y)=0.If U(y)=0 and V(y)=0 are adjoint boundary conditions of each other,then L and L′are formal adjoints of each other.

ProofFor all y∈ D(L),z∈ D(L′),we have U(y)=0,V(z)=0.Since U(y)=0 and V(z)=0 are adjoint boundary conditions of each other,by Theorem 3.1,there is

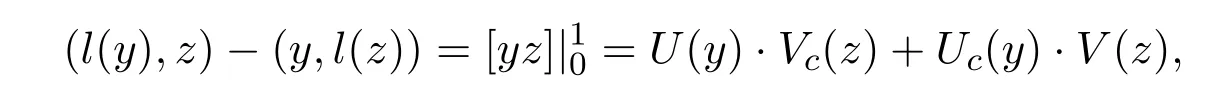
so we conclude that(l(y),z)−(y,l(z))=0,that is(l(y),z)=(y,l(z)),for any y∈D(L)and z∈D(L′).Therefore,L and L′are formal adjoints of each other.

Theorem 3.3Let the domain of L be defined by U(y)=0.If U(y)=0 is self-conjugate,then L is a Hermitian operator.

ProofFor the above U(y)and any of its complementary boundary type vector Uc(y),there exists one and only one V(z)and Vc(z),satisfying

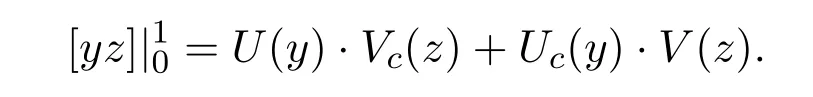
Since U(y)=0 is self-adjoint,there is a non-singular matrix C satisfing V(z)=CU(Z).Therefore,

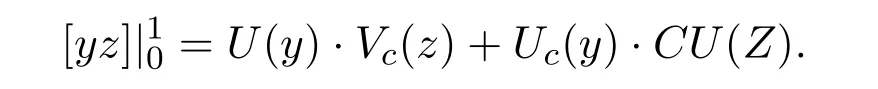
For all y,z∈D(L),we have U(y)=V(z)=0.Therefore,(l(y),z)−(y,l(z))==0.So

We conclude that L is a Hermitian operator.

Theorem 3.4Let U(y)=AC(y)0+BC(y)1and V(y)=SC(y)0+TC(y)1be an r-dimensional and the corresponding(4−r)-dimensional boundary type vectors respectively,if

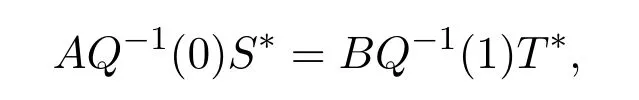
then U(y)=0 and V(y)=0 are adjoint boundary conditions of each other,where Q(x)is a fit matrix of l(y).

ProofWe only need to prove that if there are(4−r)×2 matrices S1and T1with rank(S1⊕T1)=4−r,which satisfy AQ(0)−1=BQ(1)−1,then we can find a non-singular matrix C satisfying S1=CS,T1=CT,thereby

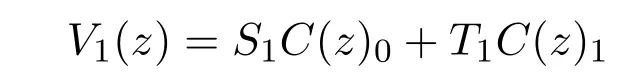
is equivalent to V(z).So U(y)=0 and V(y)=0 are adjoint boundary conditions of each other.

Since we assume that rank(A⊕B)=r,the linear space spanned by r linearly independent row vector of(A⊕B)is denoted by T.Since

we have

which shows that the column vectors of matrix

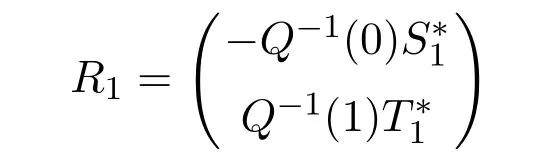
all belong to T⊥.Since

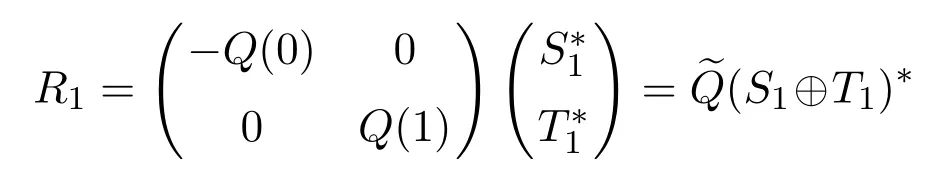
and rank(S1+T1)=4−r,we conclude that rankR1=4−r,which shows that all(4−r)column vectors of R1are linearly independent,therefore they make up the basis of T⊥.

Since S,T and S1,T1satisfy the above conditions,we can get that the rank of matrix

is(4−r),and all(4−r)column vectors make up the basis of T⊥.Therefore we can find a(4−r)×(4−r)non-singular matrix C satisfying S1=CS,T1=CT,and this shows that V1(z)is equivalent to V(z),thereby U(y)=0 and V(y)=0 are adjoint boundary conditions of each other.

Corollary 3.1If the boundary condition U(y)=AC(y)0+BC(y)1satisfies AQ−1(0)A∗=BQ−1(1)B∗,then U(y)=0 define a Hermitian operator.

Lemma 3.1is an operator from AC2(0,1)into L2(0,1).

ProofThe operator

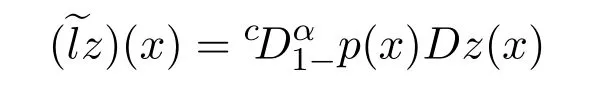
could be rewritten as

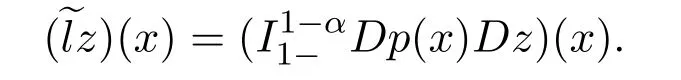
We known that,for the two-order Sturm-Liouville operator,the maximum operator map AC2(0,1)into L2(0,1).So when z(x)∈AC2(0,1),(Dp(x)Dz)(x)∈L2(0,1).By Corollary 3.1,

Remark 3.1By the definition of fractional derivative,l(y)can be rewritten as

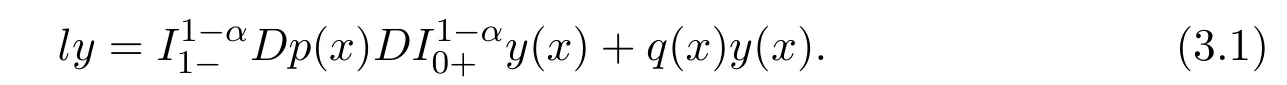
In order to make sure that l is an operator on L2[0,1],we con fine that z(x)=belongs to AC2[0,1],since we limit∈AC[0,1]in the definition of DM.Based on the above discussion,we describe DMin more detail:

Consider a subspace of DM:

Now we define a new operator:

Theorem 3.5T is an invertible operator from E to AC2[0,1],further,T−1=

ProofBy Lemma 2.4,when y(x)∈E⊆L2(0,1),

Lemma 3.2Space AC2[0,1]is a subspace of AC[0,1].

ProofFor all y(x) ∈ AC2[0,1],|y′(x)|has a upper bound K,therefore y(x)is a Lipschitz continuous function on[0,1],thus it belongs to AC[0,1].

Corollary 3.2AC[0,1]is a dense subspace of L2(0,1).

ProofFor the second-order Sturm-Liouville operator,the minimum operator domain

is a dense subspace of L2(0,1),howeveris a subspace of AC[0,1].

Theorem 3.6The maximal operator LMis a densely defined operator.

ProofSince E is a subspace of DM,it is necessary to prove that E is a dense subspace of L2(0,1).

For all y(x) ∈ TE,by Lemma 2.1,Denote F=D(TE),then E=F.By Lemma 2.3,is a bounded operator on L2(0,1),thus we only need to prove that F is a dense subspace of L2(0,1).In fact,TE={z(x)∈AC2[0,1]|z(0)=0},by Lemma 2.6,D(TE)=D(AC2[0,1])=AC[0,1].By Corollary 3.2,it is a dense subset of L2(0,1).

Theorem 3.7The minimal operator Lois a densely defined operator.

ProofAccording to the definition of Minimal operator,

thus

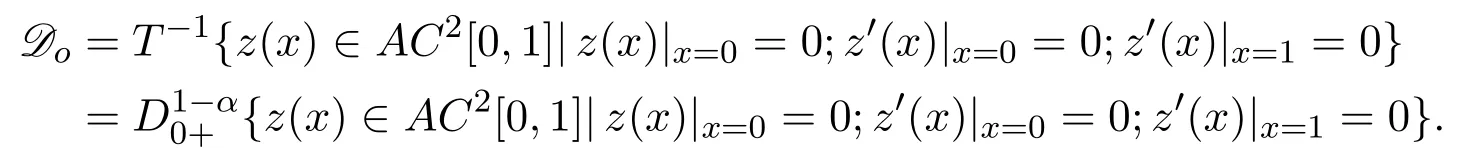
Similarly to the above discussion,we obtain

By Corollary 3.2,

is a dense subspace of L2(0,1).Combined with the boundedness of,we finish the proof.

Remark 3.2If we con finey(x)|x=1=0 in addition,that is

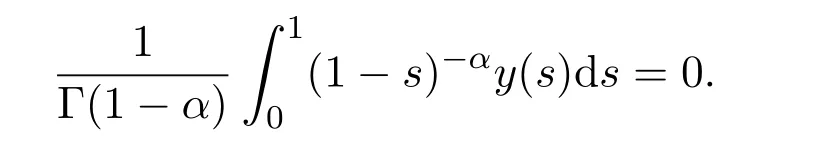
When These functions can not be dense in L2[0,1],since=0 does not hold in the definition of minimal operator.

Theorem 3.8The boundary conditions of l(y):

satisfing

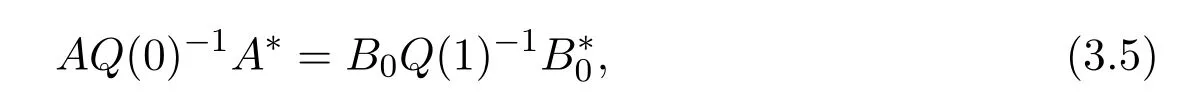
generate a symmetry operator by l,where

ProofSince the minimal operator Lois a densely defined operator,that is,

is a dense subspace of L2(0,1),therefore the functions with

are dense in L2(0,1),thus the functions with

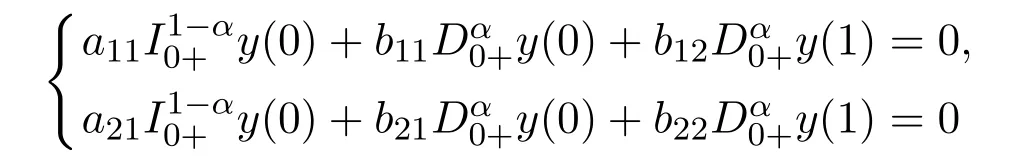
are also dense in L2(0,1).

By Theorems 3.3 and 3.4,if

the operator with the above boundary condition is symmetry.

[1]R.Hilfer,Applications of Fractional Calculus in Physics,World Scientific,Singapore,2000.

[2]R.L.Magin,Fractional Calculus in Bioengineering,Begell House Inc,2006.

[3]A.A.Kilbas,H.M.Srivastava,J.J.Trujillo,Theory and Applications of Fractional Differential Equations,Elsevier,Amsterdam,2006.

[4]D.Baleanu,Diethelmk,E.Scalas,J.J.Trujiuo,Fractional Calculus Models and Numerical Methods,Series on Complexity,Nonlinearity and Chaos,Boston World Scientific,2012.

[5]F.Mainardi,Fractional Calculus and Waves in Linear Viscoelasticity,Imperial College,London,2010.

[6]M.Klimek,O.P.Agrawal,Fractional Sturm-Liouville problem,Computers and Mathematics with Applications,66(2013),795-812.

[7]Jing Li,Jiangang Qi,Eigenvalue problems for fractional differential equations with right and left fractional derivatives,Applied Mathematics and Computation,256(2015),1-10.

[8]Zhijiang Cao,Ordinary Differential Operator,Science Press,China,2016.(in Chinese)