融合集群度与距离均衡优化的K-均值聚类算法

王日宏，崔兴梅

(青岛理工大学 计算机工程学院，山东 青岛 266033)(*通信作者电子邮箱rihongw@126.com)

0 引言

随着信息时代的发展，现有的技术手段无法实时满足海量文本数据的要求，出现了一种“知识匮乏”困局。聚类作为数据挖掘的一个重要技术方法，目前已成为一大研究热点。聚类分析不同于其他挖掘方法，它的优势主要体现在可以直接根据文本信息的自然分布状态而挖掘出有用的信息[1]。按照特定方法，实现聚类后同类数据之间的相似性大，不同类间的相似性小。

K-均值聚类(K-means clustering)算法作为一种比较典型的聚类分析算法而备受关注，并广泛应用于文本聚类分析[2-3]、客户细分[4]、交通管理[5]等实际应用领域。文本聚类分析的目标则是通过衡量文本相似度，进而将杂乱的文本集分成几个特定要求的类，实现同一类文本数据间的相似性大，不同类间的文本相似性小。然而传统的K-均值算法具有初始簇中心选择敏感、易受孤立点影响、易陷入局部极值、聚类结果不稳定等缺点，致使聚类效果不佳，无法取得理想实验效果。针对传统K-均值算法存在的缺点，各种K-means改进算法纷纷涌现，主要从获得最佳聚类中心与最好聚类数目这两方面进行优化[6-9]。樊宁[4]通过动态调整聚类数k的值，并采用密度半径来优化初始聚类中心选择，但其客户分类准确率有待提高。黄韬等[10]通过对原数据集多次采样，并进行k个质心的聚类运算，达到优化选取初始聚类中心的目的，但存在参数点的选取对聚类影响不明确的不足。翟东海等[11]基于最远样本选取策略，采用最大距离法优化选择初始簇点并应用于文本聚类，效果虽有所改善，却未考虑选取初始簇中心的代表性。周爱武等[12]针对簇中心与孤立点的问题，采用距离和方法改进聚类算法，降低孤立点的影响程度，聚类效果显著改善，而在查找孤立点时，会增加时间消耗。王春龙等[13]针对聚类结果不稳的缺陷，基于隐含狄利克雷分布的优化选取对文本集影响最大的主题，实验减少了迭代次数，聚类效果明显，但无法适应高精度文本聚类的要求。安计勇等[14]引入置信半径，并基于权重距离且采用轮廓系数优化聚类效果，最终取得较好聚类质量，但算法总耗时有所增加。李武等[15]提出基于数据空间分布选取初始簇中心，按照差异度的大小优化选择，提高聚类稳定性与收敛性，而改进算法时间复杂度不太理想。张素洁等[16]引入误差平方和来选取聚类数K值，并基于密集区域且簇中心相距较远选择初始策略，实验聚类准确率较高，但未考虑各簇中心点总的度量距离。

为了降低K-均值算法受初始簇中心选择的影响程度，使文本聚类呈现较稳定的状态，本文基于“集群度”优化选择思想，并且在初始聚类中心选择过程中，同时遵循已选择的所有簇中心距离总和最小原则，提出一种融合集群度与距离均衡优化选择的K-均值聚类(K-Means clustering based on Clustering degree and Distance equalization optimization,K-MCD)算法。针对K-均值算法对初始聚类中心选择的随机性与敏感性，在此通过基于“集群度”思想并融合所有簇中心的距离总和的均衡度量选取策略，优化初始聚类中心，来改善文本聚类效果。通过选取文本数据集对本文中的改进算法进行验证，从算法精确度与稳定性方面进行实验验证，仿真结果表明，K-MCD算法可取得较好的实验效果，且稳定性好。

1 K-均值聚类算法及文本表示

K-均值聚类算法作为一种典型的基于距离的聚类算法，用相似度标准来衡量聚类的效果，样本距离之间的大小程度决定了是否能归属同一类别，使得聚类后，样本之间的聚类距离总和最小，进而得到最佳的效果。K-均值算法先随机选取初始簇中心，然后分类样本数据对象，并计算聚类相似度大小，不断更新迭代进行，达到最大类间及最小类内相似度聚类效果。K-均值算法在随机选择初始簇中心时，可能会影响算法整体的聚类稳定性，文本聚类效果不理想。本文主要针对传统K-均值算法初始簇中心选择的敏感问题，改进并提出K-MCD算法，并运用于文本聚类研究。

1.1 文本向量化表示

文本无法直接被计算机识别并处理，要想将文本按照指定要求划分为多个簇，实现文本聚类，通常运用向量空间模型(Vector Space Model, VSM)方法[17-18]，即将文本进行向量化处理，转换成计算机能够识别的形式，再计算出文本的相似度，方可进行文本聚类分析。

VSM方法便是把指定的文本表示成特定向量的形式，而文本是由特征词体现出来的，并将其作为文本的表示单位。文本向量的维数与文本特征词在其中的权重大小相互对应。即文本集X={x1,x2,…,xn}，向量xi的向量空间形式是{w(t1,xi),w(t2,xi),…,w(tj,xi),…,w(tm,xi)}，其中，m是文本特征值的总数目，w(tj,xi)表示含义是第tj个特征词在文本xi中的权重大小。对于特征词的权重值的计算方法，通常选用TF-IDF(Term Frequency-Inverse Document Frequency)策略[19-20]。公式如下所示：

(1)

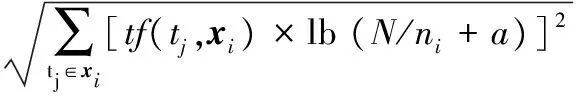
1.2 文本相似度计算

文本相似度作为统计文本之间相似程度的一个重要指标，想要进行文本聚类分析，必须构造出一种恰当的度量办法，能把文本相似程度转变成文本之间的距离来实现。由文献可知，常见的转换方法有3种，即距离函数法、余弦法与内积法。本文选取距离函数的方法来衡量文本的相似程度，其中，距离采用常用的欧氏度量办法，并且遵循文本相似度与文本距离成反比的原则，即随着文本相似程度越大，文本之间的距离就会越小，取得的文本聚类效果便越好。度量公式如下所示：

(2)

其中，w(tk,xi)与w(tk,xj)分别表示tk个文本特征在xi与xj的特征权重值。

2 K-均值初始聚类中心改进算法——K-MCD

2.1 改进算法思想及相关定义

由于K-均值算法容易受到初始簇中心选择的影响：一方面，算法的波动性可能会造成文本聚类效果不好，存在容易陷入局部解的缺点；另一方面，算法表现出总的迭代次数增加，系统开销相对增大，效率低下，同时也会导致聚类结果的不稳定性。在此，需要对初始簇中心的选取进行改进，寻找最佳聚类效果，本文主要基于以下两点改进算法策略：

1)基于“集群度”思想。总体来讲，想要取得较好的文本聚类效果，需要遵循集群度的策略办法，即选取的各个簇中心能够体现文本集的汇集程度，既能保证初始聚类中心的代表性，又能确保不会过度集中。相似度较大的文本更大概率地被分到同一个簇中，反之，相似度较小的文本更大概率地被分到不同的簇集中。

2)基于簇中心点间的度量总和优化选择策略。在优化选择初始簇中心的过程中，需要寻找一个划分的尺度，即基于初步筛选出的对象最终确定出各个簇中心，确保簇中心的分散度，使得文本总的相似度最大(文本相距度最小)。本文提出一种基于距离总和均衡优化选择的度量办法，既保证按照策略1)中“集群度”办法选取簇中心的集中代表性，又能确保文本聚类整体相似度的最优化与稳定性。

对于文本集X={x1,x2,…,xn}，本文给定几个相关定义形式。

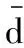
(3)

其中：d(xi,xj)表示文本xi与xj之间的度量距离，n是文本集中的文本对象的总数目。

定义2 文本聚类评价函数E：

(4)

其中：c1,c2,…,ck为k个簇中心，d2(xp,cj)为簇Cj中任意文本对象xp与相应聚类中心cj之间的度量距离的平方和。

定义3 文本聚类适应度函数f(x)：

(5)

其中：λ为任意常数；k为簇的总数目；d2(xp,cj)为簇Cj中任意文本对象xp与相应聚类中心cj之间的度量距离的平方和。

2.2 K-MCD算法

2.2.1 基于“集群度”初步筛选初始聚类中心

由于K-means算法对初始簇中心选取具有较大的敏感性，簇中心选取的不同，聚类结果可能会有比较大的差异性，如果选取不当，甚至还会造成一些错误情况的发生。为了文本聚类的准确与稳定性，在此基于“集群度”初步筛选初始聚类中心集合D。

关于“集群度”的定义方式，给定如下形式。

以二维随机文本数据分布图为例，如图1所示，选取其中的一个样本点作为代表簇中心，并且以distr作为覆盖区域的长度，计算落在覆盖区域圆内的相应文本数据点的数目，该数目便是此文本对象的集群度值。通过此种选择方式便得到相应对象点的集群度值，并依次选择l(k≤l≤n)个作为最初的文本聚类中心点。操作步骤如下：

图1 二维文本数据分布

步骤1 初始覆盖域长度distr的确定。随机选取k个数据点，记录并连续取三次，按定义1计算这些数据点两两之间的平均距离并取均值，得到：

且d(xi,xj)表示文本xi与xj之间的度量距离，在此把计算的距离作为distr的值。

步骤2 计算并选取l个初始文本对象。按照“集群度”思想，选取l个初始文本对象，并依次按值的大小由高到低的顺序排列为m1,m2,…,ml(k≤l≤n)，并存于集合M中，且|ml|表示集群度值。选取集群度值最大的m1定义成第一个簇中心点p1，并加入集合D内，同时计算得到m1和m2的文本度量距离d(m1,m2)。

步骤3 如果d(m1,m2)≥distr，那么选取集群度值次大的文本对象m2成为第二个簇中心点p2加入集合D中；否则继续判断下一个文本对象。

The weight matrix is determined by the path of packet forwarding, while the congestion distribution plays a prominent role in the LNoC. Even though congestion-aware schemes produce extra LR, they are able to alleviate uneven congestion for NoC to reduce the LNoC.

步骤4 依次判断下面的文本对象。判断m3与前两个簇中心点之间的度量距离，如果max[d(m3,m1),d(m3,m2)]≥distr，即可选择m3作为第三个簇中心p3；否则舍弃，继续判断。对于下面的点依次进行判断，并选取得到l个初始文本簇中心，得到集合D={p1,p2,…,pl}。

按此“集群度”方法初步筛选出l(k≤l≤n)个初始文本簇中心，优化选取初始簇中心的集合，一方面，体现文本集的汇集程度，从密集区域选择簇中心，加大同一簇内的优化效果；另一方面，又考虑到初始簇中心点的分散性，体现出文本集类间相似度小。基于“集群度”的选择能初步改善K-均值算法不易受初始文本簇中心选择的影响，但此办法中未涉及算法整体的文本聚类效果。为更好地应用于文本聚类，必须综合考虑文本综合相似度量。下文将对该算法作出进一步的改进策略。

2.2.2 融合距离总合均衡优化选取初始聚类中心

根据上文基于“集群度”策略优化初始聚类中心，筛选得到包含l个初始文本簇中心的集合D。在此基础上，综合考虑文本簇中心的距离总和的度量选择，进一步优化确定k个初始簇中心点，确保聚类问题整体的效果与算法的稳定性。

下面选取4个簇数目为例，如图2所示。融合“集群度”与距离总和均衡优化选取的办法，最终确定k个初始簇中心，过程如下：

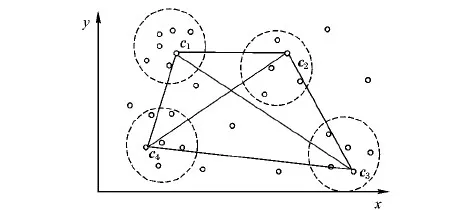
图2 初始簇中心选择

步骤1 按“集群度”方法初步筛选出l个初始文本聚类中心，并将其保存在文本对象D集合中，且D={p1,p2,…,pl}。

步骤2 选取第一个初始文本簇中心对象。按“集群度”思想选取的l个初始文本对象集合D={p1,p2,…,pl}，选取集群度值最大的p1定义成第一个簇中心点(如图2中的c1)，并从集合D中删除，同时计算得到p1和p2的文本度量距离d(p1,p2)。

步骤3 选取第二个初始文本簇中心点。对于集合D中任意文本对象pi，假如存在对象p2，满足u*d(p1,p2)+(1-u)*|p2|≥u*d(p1,pi)+(1-u)*|pi|(i=3,4,…,l)，其中，|pi|表示文本对象pi的集群度值，u为权衡调节因子(取任意常数)，那么选取度量值(以融合集群度值与距离总和均衡选择为标准)最大的对象p2作为第二个聚类中心(如图2中的c2)，并将p2从集合D中删除。

步骤4 依次判断下面的文本聚类中心点。对于集合D中剩余的任意文本对象pi，假如存在对象p3，满足{u*d(p1,p3)+(1-u)*|p3|}+{u*d(p2,p3)+(1-u)*|p3|}≥{u*d(p1,pi)+(1-u)*|pi|}+{u*d(p2,pi)+(1-u)*|pi|}(i=4,5,…,l)，即可选择p3作为第三个簇中心c3，并将p3从集合D中删除；否则继续判断。对于下面的文本对象点按同样的方式依次进行判断选择，最终得到k个初始文本簇中心，即c1,c2,…,ck。

按照以上所述选取初始文本簇中心点的方法，既能保证簇中心的文本密集域的代表性，又能权衡簇中心的分散度(用文本待初始聚类点间的度量总和衡量)，综合考虑文本初始聚类效果的最大优化度。K-均值算法初始聚类中心点的改进，优化选择相对比较密集区域且具有一定分散性的初始聚类点，为进一步应用于文本聚类分析提供最佳初始条件。

2.2.3 优化选取初始簇中心算法流程

优化选取k个初始聚类中心算法的流程，如图3所示。

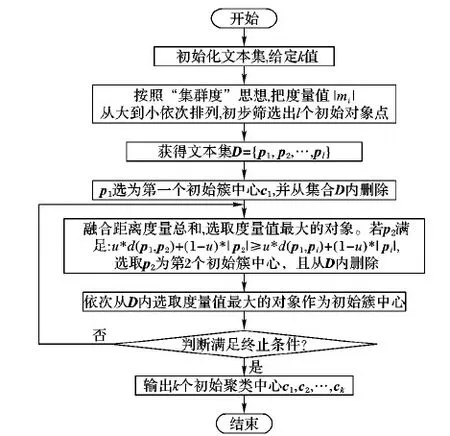
图3 优化选取初始簇中心流程

2.3 K-MCD算法进行文本聚类

K-MCD算法进行文本聚类过程如下：

Input:文本集X={x1,x2,…,xn}，聚类数目k，最大迭代次数T。

Output:划分的k个类别的簇。

步骤1 按照2.2.2节中优化选取初始簇中心的方法，得到k个初始文本簇中心，即：c1,c2,…,ck。

步骤2 对其他的文本对象，按照式(2)中文本相似度量方法，计算该文本xp到簇中心cj的距离为:

步骤3 分配各文本对象到相距最近的簇中心所代表的簇Cj中。

步骤4 修正各簇中心，根据式(6)优化选取最佳文本簇中心。文本聚类评价函数采用2.1节中的式(4)计算，文本适应度函数采用式(5)计算：

(6)

其中：Cj是第j个簇；cj与xp分别表示聚类中心点与簇内任意文本对象；cj′为该簇内其他待判断的聚类中心点。

步骤5 判断算法终止条件。如果算法达到最大迭代次数T或者执行修正操作后的簇中心几乎保持不变，此时用适应度函数的变化来衡量，即|ft+1(x)-ft(x)|≤e(ft+1(x)与ft(x)分别为第t+1次与t次的文本适应度函数值，e为趋向于无限小的数值)，则算法结束；否则继续执行步骤2，直到满足条件为止。

K-MCD算法文本聚类流程如图4所示。

图4 文本聚类流程

3 文本数据集仿真实验

3.1 实验1——算法精确性测试

为验证K-MCD算法文本聚类效果，本实验分别采用传统的K-均值算法、文献[11]改进算法、文献[18]改进算法、K-MCD算法进行实验分析比较。其中，文献[11]基于最大样本距离的策略选取初始簇中心，重新构造文本测度函数并应用于文本聚类，在选取初始簇中心时未考虑样本点的密集程度，可进一步优化算法；文献[18]通过动态调整惯性权重w及云变异策略改进粒子群算法，提高文本聚类全局搜索能力，而控制w参数的选择有些局限，聚类稳定性有待于提高。从腾讯网上选取测试文本数据集，每组数据集分别关于时尚、新闻、娱乐等几大类别主题，实验中使用的文本数据集如表1所示。

表1 实验中使用的文本数据集

本实验采用大多数聚类分析所用的F-measure的衡量方法，其中涵盖了查全率(Recall)和查准率(Precision)两个衡量方面。由类别i和j归属的类别主题，Recall衡量文本聚类分析覆盖的完备度，定义形式如式(7)所示：

Recall(i,j)=Nij/Nj

(7)

Precision则是衡量文本聚类分析查找的精确度，定义形式如下：

Precision(i,j)=Nij/Ni

(8)

其中：Nij表示类别主题j在类别i的文本数目；Ni为分类i的文本总数目，Nj为类别主题j的总数目。且类别i的聚类结果用如下形式进行定义，如式(9)所示：

(9)

文本聚类结果是用类别i的加权平均值来衡量。如式(10)：

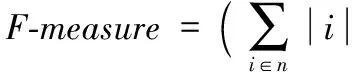
(10)

其中|i|指的是文本分类的数目。

为了更能证明文本实验数据的有效性，对给定的数据集分别测试10次，取这10次的平均值作为最终的F-measure测量值，并记录在表2中。

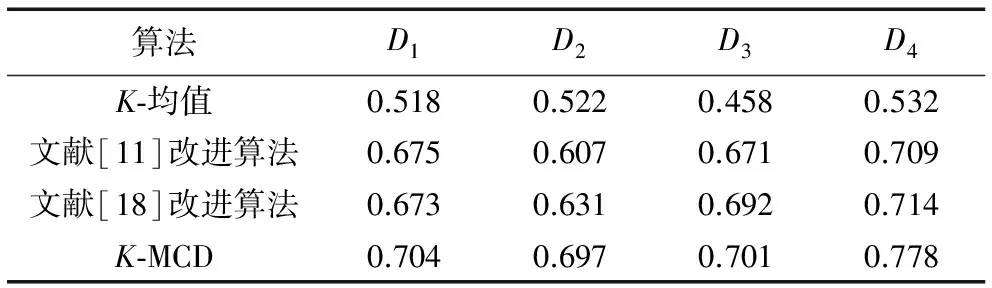
表2 各算法的F-measure实验结果

为了便于直观分析传统的K-均值算法、文献[11]改进算法、文献[18]改进算法、K-MCD算法的文本准确度聚类效果，把实验结果汇总成算法的F-measure值柱状分布图形式，如图5所示。

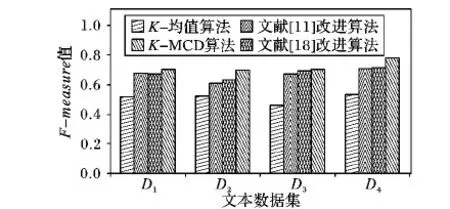
图5 各算法的F-measure柱状图

由图5可知，从整体柱状分布情况可以看出，在各类文本数据集上，本文提出的K-MCD算法的聚类精确度要高于其他3种算法，且相比传统的K-均值算法来说，F-measure值提高的幅度较明显，K-MCD算法在4个文本集上的F-measure值分别提高了18.6、17.5、24.3与24.6个百分点，取得较好的聚类精确度，且在文本集D4上的效果最明显。对比文献[11]与文献[18]中的改进算法，K-MCD算法都在文本集D2上的F-measure值增长幅度最大，分别提高了9与6.6个百分点，其次便是在文本集D4上，K-MCD算法的F-measure值分别提高了6.9与6.4个百分点。

从图中可以看出，对于不同的文本数据集，文本采用的K-MCD算法中的精确度也都有不同程度的提高。文本集D1从K-均值算法中的聚类精确值0.518提高到了0.704，约提高了18.6个百分点，效果明显，而且相比文献[11]以及文献[18]提到的改进算法，F-measure值相应地都提高了2.9%与3.1%；同样在文本集D2上呈现出良好的聚类准确性；对于文本集D3，K-MCD算法与文献[11]与文献[18]提到的算法的聚类精确度比较，聚类准确性效果不是很显著，尤其在对比文献[18]中的算法仅增加了0.9个百分点，但相比K-均值算法有较大的改善效果，增长了超过20个百分点。其中，本文中的K-MCD算法中的F-measure值在D1、D3、D4三个数据集上面超过了0.7，并且在文本集D4上达到0.778的最大精确度值。总的来说，本文中的K-MCD算法聚类准确性改进效果明显。

3.2 实验2——算法稳定性测试

本实验采用的文本数据集是从中文分类语料库(http://www.sogou.com/labs/)中选取的1 500篇测试文档，包括关于教育、军事、体育等共5类，每类300篇。分别采用传统的K-均值算法、文献[4]改进算法、文献[11]改进算法、K-MCD算法进行实验分析比较。其中，文献[4]采用有效指数法调整聚类数，并结合自适应密度半径优化初始簇中心选择，提高聚类速度，但算法改进需要更切合实际客户需求；文献[11]算法思想同实验1所述。每种算法运行50次，对该文本集测试多次，分别记录适应度函数值f(x)、算法收敛时的最大迭代次数及进化代数方差三者的最小值、最大值及其平均值的数据情况(测试得到的大小均值分别用fmin、fmax、fave以及min、max、ave表示)，且式(5)中λ取值为100，各算法实验情况如表3所示。

表3 各算法的实验测试结果

由表3可知，本文提出的K-MCD算法聚类稳定效果明显，稳定性较好。在平均进化代数方差方面，K-MCD算法比K-均值算法降低了36.99个百分点,相比文献[4]与文献[11]中提到的算法，也分别降低了8.28个百分点与4.22个百分点。文本相似度越大，评价函数之间的度量距离越小，文本的适应度函数值会越大，算法的聚类效果便越好。K-MCD算法的适应度平均值为7.201 1，明显高于传统的K-均值算法中的6.581 7，且相对于文献[4]和文献[11]中的改进算法，K-MCD算法平均适应度值分别增加9.93个百分点与12.3个百分点的良好改善效果。文献[11]中的改进算法相比文献[4]提到的算法来讲，虽然平均适应值略小，不过平均进化代数方差小，稳定性更好，整体效果比较好。从算法整体的最大迭代次数上来看，K-均值算法平均30次达到稳定收敛，本文中的改进算法可在22次内达到最大收敛效果，并且K-MCD算法的波动范围相对较小，能降低K-均值算法本身受初始簇中心选取的影响，稳定性能提高。

同时，根据K-均值算法、文献[4]中的改进算法、文献[11]中的改进算法及K-MCD算法在此文本数据集上平均适应度值随迭代次数的走势变化，绘制各算法的收敛图，如图6所示。

由图6可知，从图像的整体走势来看，本文提出的K-MCD算法相比传统K-均值算法有比较明显的聚类收敛性，在算法迭代初期，改进初始簇中心策略的引入可以较大程度地提高算法快速收敛的能力，虽然比文献[4]、文献[11]中提到的改进算法迭代初期没有较大程度的改善，不过在算法迭代5次之内，K-MCD算法有较快寻找最优解的趋势，能有效避开局部最优区域。文献[11]中的改进算法相比文献[4]中的算法来讲，虽然平均适应值略小，不过在迭代10～20次内能较快地趋于最优解的寻找，稳定性能更好，并且从图中可以看到，相对于K-均值算法适应度值缓慢增长来说，本文中的K-MCD算法文本聚类优化效果比较明显，且K-MCD、文献[4]及文献[11]中提到的这3种算法的平均适应度值达到7以上。在算法迭代后期，K-均值算法需要迭代30次才能达到最终收敛，K-MCD算法能在有限的迭代次数22次内趋于稳定状态，文本聚类稳定性能比较好。

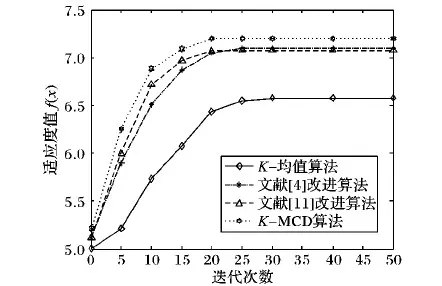
图6 各算法在文本集上的收敛图

4 结语

K-均值算法前期容易受到初始簇中心波动性的影响，在文本聚类中可能会导致聚类效果不精确与不稳定。本文基于集群度思想，筛选出具备代表性且汇集度较好的对象，进一步融合距离优化策略，从中确定出初始簇中心点，能克服K-均值算法前期簇中心选择敏感性的缺点，避开局部解区域，减少迭代次数，并趋于稳定收敛状态。对文本数据集进行向量化表示，将文本相似度转化为文本距离度量法，基于改进的K-MCD算法，重新优化选择初始文本簇中心，从精确性与稳定性两个方面进行本文数据集的验证。仿真实验证明了本文提出的K-MCD算法有较好的文本聚类效果与收敛性。对于文本聚类的向量转化及K-均值算法中待分类数目的判断有待于进一步研究。

References)

[1] 彭京,杨冬青,唐世渭,等.一种基于语义内积空间模型的文本聚类算法[J].计算机学报,2007,30(8):1354-1363.(PENG J, YANG D Q, TANG S W, et al. A novel text clustering algorithm based on inner product space model of semantic [J]. Chinese Journal of Computers, 2007, 30(8): 1354-1363.)

[2] MAHDAVI M, ABOLHASSANI H. HarmonyK-means algorithm for document clustering [J]. Data Mining & Knowledge Discovery, 2009, 18(3): 370-391.

[3] 王永贵,林琳,刘宪国.结合双粒子群和K-means的混合文本聚类算法[J].计算机应用研究,2014,31(2):364-368.(WANG Y G, LIN L, LIU X G. Hybrid text clustering algorithm based on dual particle swarm optimization andK-means algorithm [J]. Application Research of Computers, 2014, 31(2): 364-368.)

[4] 樊宁.K均值聚类算法在银行客户细分中的研究[J].计算机仿真,2011,28(3):369-372.(FAN N. Simulation study on commercial bank customer segmentation onK-means clustering algorithm [J]. Computer Simulation, 2011, 28(3): 369-372.)

[5] 高曼,韩勇,陈戈,等.基于K-means聚类算法的公交行程速度计算模型[J].计算机科学,2016,43(S1):422-424.(GAO M, HAN Y, CHEN G, et al. Computational model of average travel speed based onK-means algorithms [J]. Computer Science, 2016, 43(S1): 422-424.)

[6] LOUHICHI S, GZARA M, ABDALLAH H B. A density based algorithm for discovering clusters with varied density [C]// Proceedings of the 2014 World Congress on Computer Applications and Information Systems. Piscataway, NJ: IEEE, 2014: 1-6.

[7] YEDLA M, PATHAKOTA S R, SRINIVASA T M. EnhancingK-means clustering algorithm with improved initial center [J]. International Journal of Computer Science & Information Technologies, 2010, 1(2): 121-125.

[8] 程艳云,周鹏.动态分配聚类中心的改进K均值聚类算法[J].计算机技术与发展,2017,27(2):33-36.(CHENG Y Y, ZHOU P. ImprovedK-means clustering algorithm for dynamic allocation cluster center [J]. Computer Technology and Development, 2017, 27(2): 33-36.)

[9] 于海涛,李梓,姚念民.K-means聚类算法优化方法的研究[J].小型微型计算机系统,2012,33(10):2273-2277.(YU H T, LI Z, YAO N M. Research on optimization method forK-means clustering algorithm [J]. Journal of Chinese Computer Systems, 2012, 33(10): 2273-2277.)

[10] 黄韬,刘胜辉,谭艳娜.基于K-means聚类算法的研究[J].计算机技术与发展,2011,21(7):54-57.(HUANG T, LIU S H, TAN Y N. Research of clustering algorithm based onK-means [J]. Computer Technology and Development, 2011, 21(7): 54-57.)

[11] 翟东海,鱼江,高飞,等.最大距离法选取初始簇中心的K-means文本聚类算法的研究[J].计算机应用研究,2014,31(3):713-715.(ZHAI D H, YU J, GAO F, et al.K-means text clustering algorithm based on initial cluster centers selection according to maximum distance [J]. Application Research of Computers, 2014, 31(3): 713-715.)

[12] 周爱武,于亚飞.K-means聚类算法的研究[J].计算机技术与发展,2011,21(2):62-65.(ZHOU AW, YU Y F. The Research about clustering algorithm ofK-means [J]. Computer Technology and Development, 2011, 21(2): 62-65.)

[13] 王春龙,张敬旭.基于LDA的改进K-means算法在文本聚类中的应用[J].计算机应用,2014,34(1):249-254.(WANG C L, ZHANG J X. ImprovedK-means algorithm based on latent Dirichlet allocation for text clustering [J]. Journal of Computer Applications, 2014, 34(1): 249-254.)

[14] 安计勇,高贵阁,史志强,等.一种改进的K均值文本聚类算法[J].传感器与微系统,2015,34(5):130-133.(AN J Y, GAO G G, SHI Z Q, et al. An improvedK-means text clustering algorithm [J]. Transducer and Microsystem Technologies, 2015, 34(5): 130-133.)

[15] 李武,赵娇燕,严太山.基于平均差异度优选初始聚类中心的改进K-均值聚类算法[J].控制与决策,2017,32(4):759-762.(LIU W, ZHAO J Y, YAN T S. ImprovedK-means clustering algorithm optimizing initial clustering centers based on average difference degree [J]. Control and Decision, 2017, 32(4): 759-762.)

[16] 张素洁,赵怀慈.最优聚类个数和初始聚类中心点选取算法研究[J].计算机应用研究,2017,34(6):1-5.(ZHANG S J, ZHAO H C. Algorithm research of optimal cluster number and initial cluster center [J]. Application Research of Computers, 2017, 34(6): 1-5.)

[17] SALTON G, WONG A, YANG C S. A vector space model for automatic indexing [J]. Communications of the ACM, 1975, 18(11): 613-620.

[18] 王永贵,林琳,刘宪国.基于改进粒子群优化的文本聚类算法研究[J].计算机工程,2014,40(11):172-177.(WANG Y G, LIN L, LIU X G. Research on text clustering algorithm based on improved particle swarm optimization [J]. Computer Engineering, 2014, 40(11): 172-177.)

[19] SALTON G, BUCKLEY C. Term-weighting approaches in automatic text retrieval [J]. Information Processing & Management, 1988, 24(5): 513-523.

[20] 黄承慧,印鉴,侯昉.一种结合词项语义信息和TF-IDF方法的文本相似度量方法[J].计算机学报,2011,34(5):856-864.(HUANG C H, YIN J, HOU F. A text similarity measurement combining word semantic information with TF-IDF method [J]. Chinese Journal of Computers, 2011, 34(5): 856-864.)

This work is partially supported by the National Natural Science Foundation of China (61502262), the Shandong Graduate Education Innovation Program (SDYY16023).

WANGRihong, born in 1964, M. S., professor. His research interests include intelligent information processing, data mining.

CUIXingmei, born in 1990, M. S. candidate. Her research interests include intelligent information processing.