大图结构特征对划分效果的影响

罗晓霞，司丰玮，罗香玉

(西安科技大学 计算机科学与技术学院，西安 710054)(*通信作者电子邮箱676915315@qq.com)

0 引言

图是一种抽象数据结构类型，图的应用几乎涵盖了所有的领域，如大规模集成电路设计[1]、社交网络[2]、煤矿安全、并行计算过程中的任务分配[3-4]等。近年来，图数据的规模迅速增长，据中国互联网络信息中心(China Internet Network Information Center, CNNIC)统计，2016年Facebook在全球有15亿9千万活跃用户，并且其用户以每年几乎10%的速度增长。若将用户看作图的顶点，用户与用户之间的关系看作边，整个社交网络就变成一张巨大的图。如此庞大的社交网络图，传统的单机模式显然已经无法胜任对其的处理，因此，分布式大图处理成为了必然的趋势。如何对大规模图进行划分是影响分布式处理效率最基本也是最重要的问题之一。

大规模图的划分问题已经成为国内外的研究热点[5-7]，许多学者提出了相关的解决思路和方法，但是这些方法一般是通过优化规则迭代式的对大图划分进行调整。这种调整一方面是基于局部信息进行的，对全局的划分效果改善是有限的，另一方面需要多次迭代完成，这样导致时间开销较大，因此，这些方法并未被业界主流的分布式图数据处理系统采用。而现有算法难以对大规模图进行有效划分的一个重要原因是忽略了图结构对其划分效果的影响。例如图1(a)、(b)均包括8个顶点和12条边，但它们显然具有不同的结构特征。在均衡的二划分时，图1(a)的最优划分有0条交叉边，而图1(b)采用何种算法都会有4条交叉边。由此可见，图的结构特征对划分效果具有重要影响。

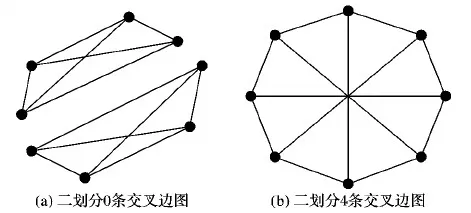
图1 8个顶点12条边不同结构特征

本文首先定义了一种描述大图结构特征的方法；然后基于真实的图数据通过不同结构特征大图生成算法(Generating Algorithm with Different Structure Features, GADSF)产生若干顶点数和边数相同但结构特征不同的仿真数据集；其次通过结构特征相似度匹配算法找到仿真图数据集与真实图之间的关系，初步证明图结构特征对真实图结构表达的有效性；随后，通过大图划分算法，得到仿真数据集与真实图数据划分结果，通过比对，进一步证明了描述图结构特征方法的有效性和正确性；最后，通过对相同顶点和边数但结构特征不同的图数据集进行划分，分析了大图结构特征与划分效果之间的关系。

1 相关工作

图划分问题是经典的NP完全问题[8]，其划分效果通常综合用交叉边个数和负载均衡来进行评价。负载均衡，即划分之后的子图规模应大致相同，以便于提高分布式处理效率。若一对存在边的顶点被划分在了不同的子图中，这条边就被称为交叉边。由于频繁跨子图访问数据会造成很高的通信代价，因此，在保证负载均衡的前提下，以降低网络通信开销为目的，交叉边的数量要尽可能少。

图划分问题是20世纪60年代初期,人们在设计大规模集成电路时将组合优化技术和图论相结合所产生的。就是将一个图的顶点集分成k个不相交的子集，且满足子集之间的某些限制[9]。最初针对图的二分问题，人们提出基于图的拉普拉斯矩阵(Laplacian)特性值对图进行二分，这种方法被称为谱方法。Barnard等[10]于1993年对谱方法进行了改进，具体是用递归谱平分法(Recursive Spectral Bisection, RSB)有效地减少了算法求解特征向量的执行时间，提高了算法的效率。

人们为了处理更大规模的图，提出了各类启发式算法。其中，比较经典的是由Kernighan等[11]提出的Kernighan-Lin(KL)算法。该算法的收敛较慢，难以处理大规模的图。在KL算法的基础上，由Fiduccia等[12]提出的Fiduccia-Mattheyses(FM)算法对KL算法进行了改进，一定程度上降低了时间复杂度，提高了收敛的速度。

随着不断的深入研究，国内外的研究者们又将许多智能优化算法(例如，遗传算法[13-14]、禁忌搜索算法[15]、模拟退火算法[16]等)应用在图的划分问题上，能够处理较大规模的图，并且在一定程度上克服了传统算法的不足；但由于这些算法忽略了图本身多变且复杂的结构特性，并没有从本质上很好地解决大规模图的划分问题。

目前也有学者对图的结构性进行研究，主要体现在图谱理论的研究。为了研究图的性质,人们引入了各种各样的矩阵,诸如图的邻接矩阵、拉普拉斯矩阵、关联矩阵、距离矩阵等[17]。人们试图通过这些矩阵的特征值性质，如谱半径、谱唯一性、能量来反映图的性质。例如：Fallat等[18]利用图的边密度来研究图代数连通度的上下界；Nikiforov[19]给出了关于图邻接谱半径的上下界；Liu等[20]研究了具有最大(小)邻接谱半径的临界图；Kharaghani等[21]给出图能量的上下界，但目前尚没有分析大图结构对划分效果的影响。

2 问题描述

本文将大图结构特征对划分效果的影响这一问题分解成了三个子问题。首先对大图结构特征进行描述；其次验证该描述方法的有效性；最后通过划分算法验证结构特征与划分效果之间的关系。

2.1 大图结构特征的描述

设有顶点数和边数相同的两个图，它们的顶点度分布不同，结构特征也不同。如图2(a)、(b)均包括20个顶点和60条边，但前者的顶点度分布较为均衡，而后者较为集中，二者具有不同的结构特征。大图结构特征实质是该图顶点度的分布特征，如何描述顶点分布特征是研究的第一个问题。

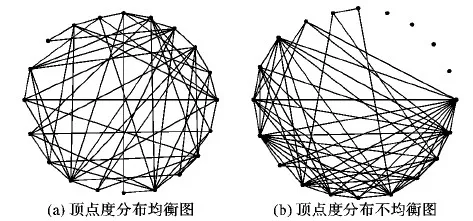
图2 20个顶点60条边不同结构特征

2.2 结构特征描述方法的有效性

图2(a)、(b)是在相同顶点数和边数但结构特征不同时，通过实验生成的一组图数据集。然而这样生成的图与真实世界的图并无直接联系，因此，需用结构特征来描述现实世界中存在的真实的图，以证明其合理性和有效性。

2.3 大图结构特征与划分效果的关系

在证明结构特征的正确性和有效性的基础之上，研究大图结构特征对划分效果的影响。在对图划分时将负载均衡作为大图划分的约束条件，交叉边数成为评价划分效果的主要指标。

3 结构特征的描述方法

现实中的大图是不断演化生成的，某点的顶点度越大，就越容易和其他顶点之间形成新的边。为了模拟真实图的产生过程，本章定义了描述结构特征的方法并且设计了GADSF。

3.1 结构特征的定义

假设初始时，所有顶点与其他顶点产生边的权重均为0，即所有顶点之间等概率产生边；当产生一条边时，这条边所关联的两个顶点的权重不再是0，而是增大，对应的这两个顶点与其他顶点产生边的概率不再与上次概率相等而是增大；之后再生成新的边时，其所关联两个顶点权重也会发生变化，同时与其他点生成新的边的概率也会对应地变化。

随着各顶点权重的变化，它们与其他顶点产生边的概率也在变化。使用变量delta来控制生成图时各个顶点产生边的概率，从而决定了该图的结构特征。

3.2 GADSF

GADSF用于生成一组顶点和边数相同但结构特征不同的图，算法的核心思想是：通过调节delta的值，当某两个顶点之间生成边时，下一次该顶点与其他顶点生成新边时的概率比其他新的顶点之间生成边的概率增大，而delta的取值影响该概率变化的幅度。

对于图G(V，E)而言，若delta=0，则所有边均为等概率生成，即每个顶点被选中的概率pk=1/V。

当delta=s(s为正整数)时，步骤如下：

步骤1 第一条边是等概率产生，假设第一次随机生成的边为(Vi，Vj)，则下一次顶点Vi和Vj被选中的概率pi=pj=(1+delta)/(V+2*delta)，而其他的顶点被选中的概率p=1/(V+2*delta)。

步骤2 假设第二次随机生成的边为(Vj,Vq)，则下一次顶点Vj和Vq被选中的概率分别是pj=(1+2*delta)/(V+4*delta)，pq=(1+delta)/(V+4*delta)，其余的k个顶点被选中的概率pk=1/(V+4*delta)；之后以此类推。

图3为V=10，E=15，delta=0,1,2,3时生成的图。图3(a)中，顶点度最大为3且边分布均衡；图3(b)中，顶点度最大为5切边分布相对均衡；图3(c)中顶点度最大为6且边的分布不均衡；图3(d)中顶点度最大为5但边分布极不均衡。

图3 10个顶点15条边不同结构特征

4 描述方法有效性验证

将欧氏距离的相似度计算应用在结构特征值相似度匹配算法中，计算真实图与仿真图之间的相似度，找到一个与真实图最相似的仿真图用以表征现实世界中真实的图，从而证明结构特征描述方法的有效性。

4.1 结构特征相似度匹配算法

现实中的大图，其顶点往往符合幂律分布，并且每个节点的划分对其整体划分效果的影响是非均衡的。若两个图顶点度分布具有相似性，则可说明这两个图具有相似性。本节依据此设计了结构特征相似度匹算法，具体步骤如下：

步骤1 计算真实图各个顶点的顶点度并降序排列记为集合D；

步骤2 从D中选出top-k个顶点(顶点度最大的k个顶点)，并将这些顶点的顶点度记为向量A(a0,a1,a2,…,ak-1)；

步骤3 将生成的仿真图数据集的每一个图也选出相同数量的top-k个顶点数记为向量B(b0,b1,b2,…,bk-1)；

步骤4 计算向量A、B之间的欧氏距离Distance并记录；

步骤5 对仿真图数据集中不同delta的图重复步骤3和4。

通过以上步骤，可找到与真实图距离最小的仿真图，即与真实图最相似的图，则该仿真图可表示真实图。

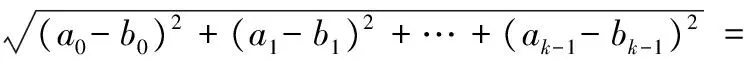
4.2 匹配实验及结果分析

4.2.1 实验数据的选取及生成

实验数据选自斯坦福大学公开的大图数据集中一个真实图G(6 301,20 777)，即该图有6 301个顶点和20 777条边。根据4.1节提出的不同结构特征大图的生成算法生成仿真数据集。令V=6 301，E=20 777，delta={0,1,2,3,4,5},Gi(0≤i≤5∩x∈R)。

4.2.2 实验结果及分析

计算出真实图G中顶点集V的顶点度并降序排列记为向量A(a0,a1,a2,…,a6300)，分别将仿真图Gi顶点集Vi的顶点度计算出，并降序排列记为向量B(b0,b1,b2,…,b6300)。从向量A、B中选取顶点度最大的k个顶点，其中k分别取63，120，180，即所取顶点是原图总顶点数的1%、2%、3%，计算Distance，实验结果如图4所示。

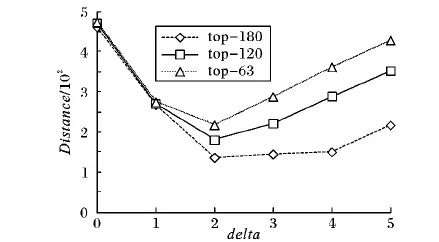
图4 结构特征相似度匹配结果

图4中3条曲线分别代表顶点数取63，120，180，delta为0,1,2,3,4,5时仿真图Gi和真实图G之间的相似度曲线图。明显地看出delta=2时，距离Distance最小，向量A、B之间距离最近，说明delta=2时生成的仿真图与真实图最为相似，由此证明描述大图结构特征的方法是有效的。

5 结构特征与划分效果之间关系

将真实图G和仿真图集Gi进行划分，通过比较划分结果再次证明大图结构特征描述方法的有效性。在此基础上，选取Hash和点对交换划分算法两种划分算法，研究大图结构特征对划分效果的影响。

5.1 大图划分算法

首先选取了Hash法中的直接取余法，其优点是可以保证划分子图之间的负载相随均衡，减少本实验的不确定因素，突出交叉边与划分效果之间的关系。其次，选择点对交换算法，该算法一种贪心算法，不从整体最优上加以考虑，每次只朝着有益的方向进行迭代，进而逼近最优解。

5.1.1 Hash划分算法

Hash划分算法就是把任意长度的输入，通过散列算法，变换成固定长度的输出。不同的关键字可能得到同一散列地址，即key1≠key2，而f(key1)=f(key2)，这种现象称为碰撞。在此选取Hash算法中的取模法，即直接取余法：f(x)=xmodk(k为非负整数)。

为给定图G(V，E)的顶点赋予唯一的标识号即变量x(x为非负整数)，然后通过取模将顶点集V划分为k个互不相交的子集V1，V2，…，Vk。当xi≠xj，而f(xi)≠(xj)时，则xi、xj所对应的顶点Vi、Vj将会被划分到同一个子图中。

5.1.2 点对交换算法

定义1 COE(Count of Original Edges)为原始交叉边个数，即将给定图G(V，E)的顶点集V，Hash划分为k个互不相交的子集V1，V2，…，Vk后，k个子集之间的交叉边数。

定义2 CEE(Count of Exchange Edges)即执行n(n为足够大的非负整数)次点对交换算法后，k个子集之间的交叉边数。

点对交换算法的具体步骤如下：

步骤1 将图的顶点集V散列的划分成V1，V2，…，Vk个互不相交的子集并且计算COE。

步骤2 从k个子图中各自选取一个顶点Si在V1,V2,…,Vk中随机交换Si并且计算CEE。

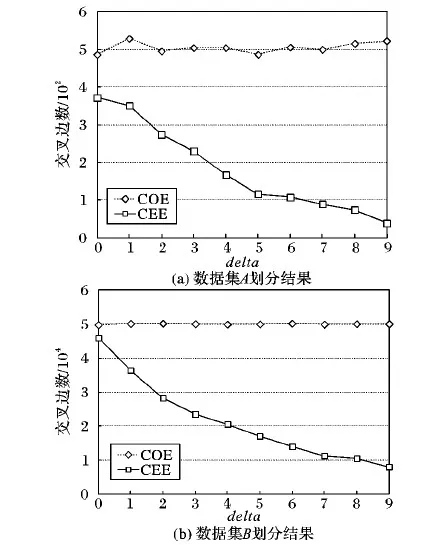
步骤3 若CEE

最后一次有效的CEE可近似地认为是划分结果的最优解。

5.2 划分实验

5.2.1 一次划分实验

由于篇幅有限，这里仅举例说明图G(V，E)，V=6 301，E=20 777，delta=2时的划分方法，其他数据集划分方法相同。步骤如下：

步骤1 将顶点集V中每个顶点赋予唯一的标识号即变量x{0≤x≤6 301∩x∈R}，在Hash划分算法中k值取2，即将图划分为两个子图V1、V2且保证负载均衡并且计算COE。

步骤2 每次将V1，V2中随机各取一个点记为Vi，Vj，设置临时变量temp用以交换Vi，Vj，记录交换后的新图并计算CEE。

步骤3 若CEECOE，则表示交换后交叉边个数没有减少，则为无效交换，将temp的值回滚给Vj恢复交换之前的状态，转至步骤2。

点对交换算法在交换足够多的次数后，能够有效地减少交叉边数量，降低通信开销。通过多次实验得出，迭代5 000次后，交叉边的个数明显减少，若连续10 000次无变化，则近似认为达到最优解，停止迭代。将真实图G和仿真图数据集Gi(0≤i≤5∩x∈R)进行划分，记录交叉边个数结果如表1(交换次数为0即为Hash划分的交叉边个数)。通过表1得出以下结果。

表1 图数据集执行两种划分算法交叉边数

1)通过Hash算法划分不同图数据集时，无论图的结构如何发生变化，交叉边数很大且无明显变化，进一步说明该算法忽略了大图结构特征对其划分效果的影响。

2)对真实图G和仿真图G2进行划分，当点对交换算法执行到5万次时，图G交叉边的个数由Hash划分的10 425条减少到4 762条；图G2交叉边的个数由10 267条减少到4 090条，且与图G与的交叉边数量最接近。由此说明了点对交换划分算法能够减少交叉边数，且描述图结构特征的方法是有效的。

3)对仿真图数据集Gi{0≤i≤5∩x∈R)执行点对交换算法5万次时，随着delta的增大即图的结构特征发生变化，交叉边数明显下降。由此说明了大图结构特征对划分效果有很大影响

5.2.2 二次划分实验

为了证明结构特征与划分效果之间的普适性，进行第二次划分实验。分别生成两组数据集A、B。

A:V=100，E=1 000，delta∈{0≤delta≤9∩x∈R}

B:V=1 000，E=100 000，delta∈{0≤delta≤9∩x∈R}

采用同样实验步骤分别将两组数据集进行划分,得出的结果如图5所示。图5(a)是数据集A执行点对交换划分算法2万次时划分结果，图5(b)图是数据集B执行5万次时划分结果。由图5可明显地看出：随着delta的增大，COE变化不大而CEE的数量明显减少，说明了图的结构特征对划分效果有着直接的影响，也就是说图的顶点度分布差异越显著，交换后的交叉边个数越少，划分效果越好。

6 结语

大图划分是实现大图分布式处理的重要基础。尽管当前已经提出大量算法来改进大图划分的效果，但均忽视了大图结构本身对划分效果的影响。本文首先提出一种描述大图结构特征的方法，并通过大量实验验证了结构特征对真实图结构表征的有效性。最后，通过划分实验分析了不同算法下大图结构特征与划分效果之间的具体关系，这对下一步建立图的结构特征与划分效果之间的关系模型奠定了基础，达到利用图结构特征预测划分效果的目标。

图5 两组数据集划分结果

References)

[1] JOHANNES F M. Partitioning of VLSI circuits and systems [C]// DAC ’96: Proceedings of the 33rd Annual Design Automation Conference. New York: ACM, 1996: 83-87.

[2] MEYERHENKE H, SANDERS P, SCHULZ C. Parallel graph partitioning for complex networks [C]// Proceedings of the 2015 IEEE International Parallel and Distributed Processing Symposium. Piscataway, NJ: IEEE, 2015: 1055-1064.

[3] KARYPIS G, KUMAR V. Parallel multilevelk-way partitioning scheme for irregular graphs [J]. Journal of Parallel & Distributed Computing, 1999, 41(2): 278-300.

[4] HENDRICKSON B, LELAND R. An improved spectral graph partitioning algorithm for mapping parallel computations [J]. SIAM Journal on Scientific Computing, 1995, 16(2): 452-469.

[5] VAQUERO L, CUADRADO F, LOGOTHETIS D, et al. Adaptive partitioning for large-scale dynamic graphs [C]// ICDCS 2014: Proceedings of the 2014 IEEE 34th International Conference on Distributed Computing Systems. Piscataway, NJ: IEEE, 2014: 144-153.

[6] HUANG J, ABADI D J. Leopard: lightweight edge-oriented partitioning and replication for dynamic graphs [J]. Proceedings of the VLDB Endowment, 2016, 9(7): 540-551.

[7] MAYER C, TARIQ M A, LI C, et al. GrapH: heterogeneity-aware graph computation with adaptive partitioning [C]// ICDCS 2016: Proceedings of the 36th IEEE International Conference on Distributed Computing Systems. Piscataway, NJ: IEEE, 2016: 118-128.

[8] GAREY M R, JOHNSON D S, STOCKMEYER L. Some simplified NP-complete graph problems [J]. Theoretical Computer Science, 1976, 1(3): 237-267.

[9] 郑丽丽.图划分算法综述[J].科技信息,2014(4):145-145.(ZHEN L L. A survey of graph partitioning algorithms [J]. Science and Technology Information, 2014(4): 145-145.)

[10] BARNARD S T, SIMON H D. Fast multilevel implementation of recursive spectral bisection for partitioning unstructured problems [J]. Concurrency and Computation Practice and Experience, 2010, 6(2): 101-117.

[11] KERNIGHAN B W, LIN S. An efficient heuristic procedure for partitioning graphs [J]. Bell System Technical Journal, 1970, 49(2): 291-307.

[12] FIDUCCIA C M, MATTHEYSES R M. A linear-time heuristic for improving network partitions [C]// 25 years of DAC Papers on Twenty-Five Years of Electronic Design Automation. New York: ACM, 1988: 241-247.

[13] FARSHBAF M, FEIZI-DERAKHSHI M R. Multi-objective optimization of graph partitioning using genetic algorithms [C]// Proceedings of the 3rd International Conference on Advanced Engineering Computing and Applications in Sciences. Washington, DC: IEEE Computer Society, 2009: 1-6.

[14] BOULIF M. Genetic algorithm encoding representations for graph partitioning problems [C]// Proceedings of the 2010 International Conference on Machine and Web Intelligence. Piscataway, NJ: IEEE, 2010: 288-291.

[15] ROLLAND E, PIRKUL H, GLOVER F. Tabu search for graph partitioning [J]. Annals of Operations Research, 1996, 63(2): 209-232.

[16] AARTS E, KORST J, MICHIELS W. Simulated annealing [J]. Metaheuristic Procedures for Training Neural Networks, 2007, 36(3): 187-210.

[17] 翟明清.图的结构参数与特征值[D].上海:华东师范大学,2010:1-5.(ZHAI M Q. Structure variables and eigenvalues of graphs [D]. Shanghai: East China Normal University, 2010: 1-5.)

[18] FALLAT S M, KIRKLAND S, PATI S. On graphs with algebraic connectivity equal to minimum edge density [J]. Linear Algebra & Its Applications, 2003, 373: 31-50.

[19] NIKIFOROV V. Note: Eigenvalue problems of Nordhaus-Gaddum type [J]. Discrete Mathematics, 2014, 307(6): 774-780.

[20] LIU H, LU M, TIAN F. On the spectral radius of unicyclic graphs with fixed diameter [J]. Linear Algebra & Its Applications, 2007, 420(2/3): 449-457.

[21] KHARAGHANI H, TAYFEH-REZAIE B. On the energy of (0,1)-matrices [J]. Linear Algebra & Its Applications, 2008, 429(8): 2046-2051.

This work is partially supported by the National Natural Science Foundation of China (41472234), the Scientific Research Program of Shaanxi Provincial Education Department (15JK1468), the Xi’an University of Science and Technology Foundation for Fostering Talents (201633).

LUOXiaoxia, born in 1964, professor. Her research interests include big data and cloud computing, software engineering, distributed computing.

SIFengwei, born in 1992, M. S. candidate. His research interests include distributed storage, graph partitioning algorithm.

LUOXiangyu, born in 1984, Ph. D., lecturer. Her research interests include distributed storage, big data.

DOI:10.11772/j.issn.1001- 9081.2017071886