面向非完全序列的水下三维传感网定位算法

车 迪，牛 强

(中国矿业大学 计算机科学与技术学院，江苏 徐州 221116)(*通信作者电子邮箱chedi@cumt.edu.cn)

0 引言

随着无线传感器网络(Wireless Sensor Network, WSN)[1]应用的日益广泛，近年来，对于无线传感器网络在水下应用的研究成为了热点。水下传感器网络[2]是一种包括声、磁场、静电场等的物理网络，其在污染预测、海洋监测、远洋开采以及海洋数据采集等方面取得了广泛的应用，更将在未来的海军作战中发挥重要的作用与优势。在基于无线传感器网络的监测应用中缺乏位置信息的数据往往没有意义，因此获取传感器节点的位置信息至关重要，对于水下传感器网络也是一样的，得到传感器节点的位置信息是其研究工作的重中之重。作为水下传感器网络的关键基础支撑技术之一，节点定位技术的研究具有极其重要的理论与实际意义[3]。

现有的无线传感网节点定位方法大多以二维空间为背景，但由于水下传感器网络的节点定位为三维空间模型，因此，本文以水下三维传感网的目标定位为着眼点。另外，绝大多数基于序列的定位算法皆以信标节点通信范围全网覆盖为研究前提，则未知节点可接收全网信标节点的通信信息，因此该种算法皆利用全序列(序列长度为信标节点数)进行节点定位，但水下传感网中，存在环境恶劣、信号传播困难以及定位空间较广等因素，所以信标节点通信范围无法达到全网覆盖，导致未知节点接收信标节点通信信息部分缺失。为解决上述问题，本文提出一种基于非完全序列(序列长度小于信标节点数)的水下三维传感网定位算法。该算法利用Voronoi图的三维空间划分方法和阶次序列定位的思想，通过虚拟信标节点、非完全序列的引入以及最邻近序列表的加权平均估算，在保证定位精度较高的前提下有效降低了算法的计算复杂度，且未带来额外的节点能量消耗以及网络成本。

1 相关工作

与其他环境下的传感器网络相同，根据定位过程中是否实际测量节点的物理距离或方位角度，水下传感器网络的节点定位算法主要分为两大类：

1)基于测距的定位算法。基于测距的定位机制通过测量相邻节点间的实际距离或方位角度来估算未知节点的位置。一般情况下，未知节点需与信标节点进行直接通信，并利用其接收到的信号强度、到达角度或到达时间差进行测距，然后再根据其与信标节点的几何关系来测算未知节点的坐标。在基于测距的定位算法中，最典型的几种测距方法为：基于接收的信号强度指示(Received Signal Strength Indication， RSSI)[4]、到达角度(Angle Of Arrival， AOA)[5]、到达时间(Time Of Arrival， TOA)[6]和到达时间差(Time Difference Of Arrival， TDOA)[7]等。

2)距离无关的定位算法。距离无关的定位算法不需要节点间的绝对测距或是角度信息，仅利用节点之间的相邻关系，依据网络的连通度以及信标节点信息进行未知节点的位置测算。目前已提出的距离无关定位算法有：质心算法[8]、近似三角形内点测试法(Approximate Point-In-triangulation Test， APIT)[9]和DV-Hop算法[10]等。

基于序列的定位算法是近几年提出的一种综合基于测距和距离无关的定位算法，其核心思想是将一个二维定位平面用已排好的信标节点通过某种方式进行空间划分，构建虚拟信标节点，并根据其与信标节点的距离次序来确定虚拟信标节点的阶次序列，即定位序列。文献[11]首次提出了WSN中基于序列的节点定位方法，利用每两个参考点之间的垂直平分线将具有n个参考点的二维空间划分为O(nn)个区域，并分别用序列独一无二地表示各个区域(由于几何约束，得到的序列实际数为O(n4))，该算法对由于无线信道的多径干扰和遮蔽效应产生的随机误差具有鲁棒性。文献[12]提出了一种三点垂心法和序列定位相结合的无线传感网中节点定位的改进算法，即通过得到序列相关系数的前三位最大值，求出与未知节点距离“最近”的三个区域的重心所构成的三角形的垂心，且过滤掉未知节点不可能处在的区域，降低了节点平均定位误差，该算法增加了估算未知节点精确位置的计算量，但无需增加算法的计算复杂度与传感器节点的硬件设备，与传统的三点垂心法与序列定位算法相比，该算法对于节点的定位精度有明显的提高。文献[13]提出了一种基于N-最优阶次序列的无线传感网节点定位方法，通过无线信号的衰减模型来产生虚拟测试点，再以参考点为样本，利用随机采样的方法确定最优N值，最后选择阶次为前N位的序列代表的区域，对未知节点的位置进行加权估算，该方法有效减少了节点的定位误差，并且能在一定程度上提高边界节点的定位精度。文献[14]提出了一种基于参考点序列的无线传感网节点定位算法，该算法将Voronoi图的顶点作为参考点，从而使信标节点的数目增加，然后利用基于参考点与信标节点到传感器节点建立的序列等级对传感器节点的位置进行估算，该算法比质心算法和DV-Hop算法具有更高的定位精度。其中，文献[12-13]在文献[11]的基础上对定位算法进行了改进，但也令其算法的复杂度有所增加，文献[14]虽首次将Voronoi图引入到基于信标节点的定位空间区域划分中，但并未考虑未知节点所处区域信标节点对定位估算的影响。

文献[15]提出了SLC3V(Sequence Localization Correction algorithm based on 3D Voronoi diagram)，一种基于Voronoi图原理与阶次序列的三维无线传感器网络定位算法，该算法利用Voronoi图对三维定位空间进行区域划分，构建虚拟信标节点的阶次序列表，并通过RSSI方法得到未知节点的定位序列，然后选择N个最优参数并对其进行等级相关系数的归一化处理，最后实现对未知节点位置的加权估计，但该算法以假设信标节点的通信半径能覆盖整个无线传感网为研究背景，这就限制了该算法只能应用于定位空间较小的网络环境，而不适用于覆盖范围较大的网络以及通信环境恶劣的水下传感网。

本文关注水下三维传感网的节点定位问题，对上述问题加以考虑，针对信标节点通信半径非全网的大规模网络，并结合Voronoi图划分原理、序列定位算法和RSD(Regulated Signature Distance)[16]算法，设计一种面向非完全序列的水下三维传感网定位(Non-Full Sequence-based Localization, NFSL)算法，实现对未知节点位置的加权估算。

2 预备知识

本章简单介绍3D Voronoi图[17]在三维定位空间中进行区域划分的原理以及基于序列的定位算法。

2.1 3D Voronoi图

Voronoi图是众多空间划分方法之一，它将空间划分成一定数量的子区域。目前，Voronoi图已被广泛应用于各个领域，比如地理信息系统、气象学以及资讯系统等。许多科研人员利用Voronoi图来研究无线传感器网络中的覆盖问题。

现给定一个二维平面上传感器离散点集合P={p1,p2,…,pn}，2≤n<∞，A(x,y)为平面上任意一点，则散点pk(xk,yk)，k∈K={1,2,…,n}与点A的欧氏距离d(pk,A)表示为：

(1)

Voronoi图基于每个散点将该平面划分为n个区域，使得每个区域有且仅有一个散点pk，且在散点pk所在Voronoi区域R(pk)中的任意点A满足下述条件：

R(pk)={A|d(pk,A)≤d(pj,A),∀k≠j∧k,j∈K}

(2)

则散点集P的Voronoi图R(P)由该平面上所有散点的Voronoi区域构成。

由上述可得，2D Voronoi图是由一组连接每两个邻点直线的垂直平分线组成的连续多边形组成，且该连续多边形无重叠、无接缝[18-19]，但随着维数的增长，构成Voronoi图的单元也由多边形变成了高维的多面体，因此，构成3D Voronoi图的单元即为一组三维多面体的集合。如图1所示，其中，实心圆点表示在三维定位空间内随机部署的10个信标节点，图示即为基于10个信标节点的3D Voronoi图。

最近邻近性为Voronoi图的特性之一[20]，即Voronoi子区域内的任意节点到该区域信标节点的欧氏距离小于到其他Voronoi子区域信标节点的欧氏距离，本文正是利用这一特性对三维定位空间进行区域划分。

2.2 序列定位算法

近年来，许多研究提出基于序列的定位方法，其高效性得益于结合了基于测距与距离无关两类算法，但目前对序列定位算法的研究大多都以二维空间作为背景[21]。由于序列定位算法在三维空间的应用原理与二维空间相同，且三维空间的图示较二维空间更为复杂，所以在这里以序列定位算法在二维空间中的应用过程为例作简单说明：

步骤1 构建二维空间的边界。

步骤2 利用每两个相邻信标节点连线的垂直平分线将边界内的区域划分为三类子区域：点、线、面。

步骤3 计算每个子区域的重心(本文将其称作虚拟信标节点)以及其与各个信标节点之间的距离。

步骤4 确定定位空间中所有虚拟信标节点的定位序列并将其归入阶次序列表中。

步骤5 计算未知节点的定位序列与阶次序列表中虚拟信标节点定位序列的等级相关系数，并选择系数值最大的虚拟信标节点序列作为距离未知节点定位序列“最近”的序列。而该“最近序列”所对应的区域重心即作为未知节点的估测位置。

图1 三维定位空间的Voronoi图

其中，虚拟信标节点的定位序列与未知节点的定位序列在后面的3.2节中会给出详细介绍，阶次序列表即包含所有虚拟信标节点的定位序列。

图2为基于4个信标节点的3种区域阶次序列确定方法的示例，其中区域1为点，区域2为边，区域3为面。如上述步骤所示，区域划分完成后，根据各个子区域的重心到4个信标节点的距离即可得到相应的阶次序列(如区域1的阶次序列为3113，区域2的阶次序列为3211，区域3的阶次序列为1243)。

相比其他基于RSSI的定位算法，基于序列的定位算法无需利用RSSI来得到具体的距离参数，它只用来确定未知节点的定位序列，故RSSI方法的固有误差对本文基于序列的定位算法影响相对较小。

序列定位算法在三维定位空间中的应用是在二维空间中应用的一种拓展与延伸，三维空间被每两个信标节点连线的垂直平分面划分出来的3种类型子区域分别为：边、面、体。

图2 基于4个信标节点的阶次序列示例

3 NFSL算法

水下传感器网络的应用场景为三维空间，且Voronoi图具有高阶模型，所以本文考虑将3D Voronoi图引入到水下传感网的应用场景中。文献[22]中提出一种基于序列加权的无线传感器网络定位算法，虽然该算法降低了边缘节点的误差以及改善了定位精度，但其应用背景为二维定位空间，不适应于水下传感网的目标定位；文献[23]提出的一种基于3D Voronoi图的序列定位算法SL3V (Sequence Localization algorithm based on 3D Voronoi diagram)和文献[15]提出的一种基于Voronoi图和阶次序列的三维无线传感器网络定位算法皆以三维传感网为背景且信标节点的通信范围都假设为全网覆盖，这就导致其无法应用于大规模三维网络或需昂贵的通信范围极大的传感器设备。

针对上述问题，本文提出一种面向非完全序列的水下三维传感器网络定位(NFSL)算法。其基本思想为：首先，利用3D Voronoi图基于三维定位空间中给定的信标节点对该区域进行划分，并将划分成的Voronoi多面体中3种区域的几何中心作为虚拟信标节点；然后，计算每个虚拟信标节点到各个信标节点的距离并得出虚拟信标节点的阶次序列以及计算每个信标节点到各个信标节点的距离并得出信标节点的阶次序列；接着，通过RSSI方法得到未知节点的非完全阶次序列，并利用该序列与所有信标节点的阶次序列作相似度比较，选择与其相似度最大的信标节点作为“最邻近”信标节点，并将该信标节点的阶次序列与其所属区域所有虚拟信标节点的阶次序列列入表中从而构建出与该未知节点相对应的最邻近序列表；最后，利用修改后的RSD算法计算未知节点序列与其对应的最邻近序列表中所有序列的相关系数，通过对该系数作归一化处理并将所得结果作为权重实现对未知节点位置的加权估计。

3.1 三维定位空间的划分

根据实际的定位环境在三维空间中构造立方体边界，且信标节点被随机分布于定位空间中。本文使用3D Voronoi图划分三维定位空间，Voronoi多面体产生后，每一个信标节点都在相应的Voronoi多面体内部。为了降低空间划分的复杂度，本文利用文献[18]中提出的快速生成3D Voronoi图方法。

区域划分完成后，三维定位空间就被每两个信标节点之间的垂直平分面分隔成了3种类型的区域，即边、面、体。如图3所示，其中，实心圆点表示三个信标节点A、B、C。

图3 虚拟信标节点阶次序列示例

3.2 阶次序列的计算

本文算法涉及到对3种序列的处理，分别为：信标节点的阶次序列(与信标节点的定位序列等同，后可类比之)、虚拟信标节点的阶次序列和未知节点的阶次序列。

3.2.1 信标节点阶次序列

作为信标节点，其位置信息皆为已知条件，那么就可以利用两点距离公式计算一个信标节点与其他信标节点的距离，根据距离的由近到远将对应的信标节点编号表达成为一个阶次序列，则由此方法可得到每个信标节点的阶次序列，记为Seq_anch。举例说明，如表1所示，已编号的5个信标节点A、B、C、D、E，信标节点A距离自己以及其他4个信标节点的距离分别为0，419.469 9，573.551 2，462.814 2，548.015 5，由于与节点A距离从近到远的信标节点编号分别为：1、2、4、5、3，所以信标节点A的阶次序列为12453。

表1 信标节点阶次序列的确定

3.2.2 虚拟信标节点阶次序列

首先，给出虚拟信标节点的定义：本文将利用3D Voronoi图划分出的3种区域(边、面、体)的几何中心作为虚拟信标节点。为了简化运算，每个区域的中心被定义如下：任何边的中心为其中点，任何面的中心根据文献[11]中的方法计算，任何体的中心为相应多面体中最远的两个点连线的中点。

在给定的三维定位空间中，信标节点的位置信息为已知，则所有虚拟信标节点的位置在区域划分完成后都已确定并可被推算出来，那么根据虚拟信标节点到各个信标节点距离的远近就可得到虚拟信标节点的阶次序列，记为Seq_vir。虚拟信标节点序列确定的具体过程与3.2.1节中信标节点阶次序列的步骤相似。

图3为虚拟信标节点序列的一个示例，图中实心圆点A、B、C表示信标节点，空心圆点D、E、F表示虚拟信标节点，且每个虚拟信标节点旁边都有一个基于距离阶次的定位序列。其中，点D为一个边的中心，由于A点到D点的距离排名为第一位(即A点距离D点最近)，且B点距离D点的距离排名为第三位(即B点距离D点最远)，所以节点D的阶次序列为132。同理，点E是一个体的中心，其阶次序列为231，点F为一个面的中心，其阶次序列为312。

3.2.3 未知节点阶次序列

不同于之前提到过的众文献假设所有的未知节点全部位于信标节点的通信范围内，本文提出的定位算法基于水下大规模三维传感器网络且信标节点的通信范围非全网覆盖。首先，全网信标节点向周围的传感器节点发送数据包，未知节点根据接收到的RSSI值得到其到各信标节点的距离次序从而划分出该点到各信标节点的位置序列等级，最终确定未知节点的阶次序列，记为Seq_unk。

在这里着重说明，由于上文提到的信标节点与虚拟信标节点的阶次序列都是基于已知的位置信息而得，所以为全序列，即序列长度为信标节点的总数；而本节提出的未知节点的阶次序列是基于RSSI方法而得，由于RSSI会受到通信范围的影响，且在大规模且通信环境恶劣的水下传感网中，信标节点通信范围很难达到全网覆盖，所以，未知节点的阶次序列多为非完全序列(即序列长度小于信标节点的总个数)。

如图4所示，N1与N2代表两个未知节点，右边的序列为其从全网6个信标节点接收到的RSSI值，其中，Inf表示未知节点不在该信标节点的通信范围内。以图中的N1为例，其RSSI序列为-147.01，-157.58，-137.25，-154.34，Inf，-156.60，由于RSSI值的大小可以粗略反映未知节点到各信标节点距离的远近，则该未知节点的阶次序列可根据RSSI值的由大到小确定，所以N1的阶次序列为3-1-4-6-2(序列不包括与该未知节点无法通信的信标节点的编号)。N2阶次序列的确定与N1同理。

图4 未知节点阶次序列示例

3.3 最邻近序列表的构建

常用的度量2个阶次序列相似度的准则为Kendall的Tau指标与Spearman的阶次相关系数，但二者的处理对象皆为等长的阶次序列，不适用于本文中的非等长序列(信标节点序列与虚拟信标节点序列均为全序列，未知节点序列为非完全序列)，因此，本文借鉴RSD算法对2个非等长阶次序列进行相似度度量并得到其阶次相关系数，由于该阶次相关系数被用作权重，所以本文对该算法稍加修改使其适应于NFSL，修改后的RSD算法可用下式表达：

(3)

其中，K为序列Sm与Sn并集的长度，SD(Sm,Sn)为显性、隐性、可能性3种翻转对数量之和[16]，则据式(3)得到的结果RSD′(Sm,Sn)即为序列Sm与Sn的阶次相关系数(即二者的相似度)，其范围为[0,1]，在3.4节中将其作为权重对未知节点的位置作加权估计。

针对给定未知节点X(x,y,z)的阶次序列S，利用式(3)计算序列S与所有信标节点序列的阶次相关系数，选择系数最大的信标节点作为未知节点X的“最邻近”信标节点Nb，并将其置于最邻近序列表T中，另外，将Nb所处Voronoi子区域中所有虚拟信标节点的阶次序列也置于T中。由此，未知节点X的最邻近序列表T={T1,T2,…,Tn}即可被确定，其中T1为信标节点Nb的阶次序列，T2到Tn为Nb所属子区域中所有虚拟信标节点的阶次序列。

3.4 未知节点位置的加权估计

给定未知节点X(x,y,z)的定位序列W，本文算法根据3.3节中介绍的方法构建X的最邻近序列表T={T1,T2,…,TN},计算出W与T中每个序列的阶次相关系数(该系数已归一化)并将其作为权重，最后结合最邻近序列表T中各个序列相对应的节点坐标进行未知节点位置的加权估计，则未知节点X(x,y,z)的坐标可表示为：

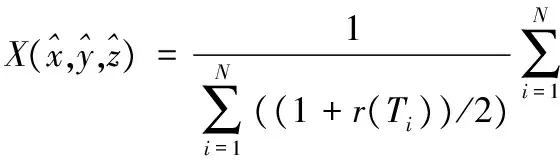
(4)

其中：r(Ti)表示未知节点序列W与最邻近序列表T中序列Ti的阶次相关系数，Ci表示T中第i个序列Ti对应的坐标。

3.5 NFSL算法伪代码展示

本节综合3.1～3.4节内容，给出NFSL的算法流程。首先，根据已知的信标节点坐标矩阵N，计算信标节点阶次序列Seq_anchi以及空间划分后所得虚拟信标节点的坐标矩阵V，根据N与V计算出所有虚拟信标节点阶次序列Seq_virj；其次，根据给定未知节点X的RSSI矩阵S，计算未知节点阶次序列Seq_unkk；然后，利用式(3)计算未知节点序列与所有信标节点序列的阶次相关系数，并取值最大的信标节点作为该未知节点的“最邻近”信标节点Nb，Nb的阶次序列记为S_anch，将Nb与其所处Voronoi子区域中所有虚拟信标节点的阶次序列置于最邻近序列表T中，其对应坐标置于坐标集C中；最后，利用式(3)计算出未知节点序列与T中每条序列的阶次相关系数r(Ti)，并将其作为权重，利用式(4)实现未知节点X位置的加权估计。

伪代码如下所示。

算法1 NFSL算法。

Input: Coordinates matrix of anchorsN, RSSI matrixS

for each anchornido

Compute theSeq_anchiof all anchors

end for

Compute coordinates matrix of vir_anchorsV

for each vir_anchorvjdo

ComputeSeq_virjof all vir_anchors

end for

Compute theSeq_unkkof all unknown nodes

for unknown nodeXdo

ComputeRSD′(Seq_unkk,Seq_anchi)

according to Eqn. (3)

ConstructCandT

Computer(Ti) =RSD′(Seq_unkk,Ti)

according to Eqn. (3)

Compute coordinate ofXaccording to Eqn. (4)

end for

Output: Coordinates matrix of unknown nodes

4 仿真结果与性能分析

本文利用Matlab仿真软件对提出的定位算法进行仿真，评估其性能，并与DV-Hop、质心算法等经典定位算法进行比较。本章采用的仿真环境为：500个节点随机分布于500 m×500 m×500 m的正方体区域内，其中，信标节点比例为0.3，节点通信半径均为200 m。以上参数均为默认值，下文仿真中除个别对比参数(如信标节点比例、通信半径、节点总数和网络规模)作为变量以外，其余变量均为默认值。另外，本文仿真结果中的定位误差是指节点的实际定位误差(m)与节点通信半径(m)的比值。如图5所示，图中所有参数皆为默认值。

图5 仿真节点分布

4.1 通信开销分析

在DV-Hop中，信标节点向邻居节点广播自身位置，接收节点记录到每个信标节点的最小跳数并转发给下一跳邻居节点，最终每一个未知节点可以得到与每一个信标节点的最小跳数；但在NFSL与质心算法中，每个未知节点仅接收通信范围内所有信标节点的通信信息而不再向邻居节点转发，由此就可获得NFSL中未知节点距离信标节点的阶次序列和质心算法中所有与该未知节点连通的信标节点位置信息。综上可得，本文算法与质心算法的通信开销大致相同，且小于DV-Hop的通信开销。

4.2 信标节点数的影响

信标节点占总节点的比例称为信标节点比例，信标节点比例的大小将直接影响本文算法的定位精度。图6(a)～(c)分别表示信标节点比例对本文提出算法、DV-Hop、质心(Centroid)算法3种算法的平均定位误差、最大定位误差与最小定位误差的影响。从图中可以发现在信标节点以0.15，0.2，0.25，0.3，0.35，0.4的比例逐渐递增的情况下，本文算法的平均定位误差由约0.32下降至约0.23，DV-Hop由约0.33微降至约0.3，质心算法则由约0.34降至约0.29，虽然3种算法的定位误差都在逐渐递减，但本文算法的定位效果提高最快。表明在信标节点比例增多时，本文算法的定位精度具有更为明显的优势。

4.3 节点通信半径、节点总数与网络规模的影响

本文算法的定位精度受多种因素影响，因此本节进一步在不同通信半径、节点总数与网络规模的情况下对算法进行了评估。图7(a)为通信半径对本文算法与经典定位算法的平均定位误差影响对比图，从图中可以看出，通信半径对3种算法的影响不尽相同，其中，随着通信半径以25 m为间隔从150 m扩大至300 m的情况下，本文算法的平均定位误差从约0.35下降至约0.17，然DV-Hop的定位精度无明显波动，质心算法的定位精度与之降低，定位误差增至约0.38左右。

图6 信标节点比例对定位误差的影响

图7(b)为本文算法、DV-Hop算法和质心算法平均定位误差在节点总数增加影响下的变化趋势。可以看出，在信标节点比例不变而节点总数以50为间隔从300增至600的情况下，本文算法的定位误差从约0.31降至约0.24，而质心算法的定位误差则由约0.33降至约0.3，对比之下，本文算法定位精度的提高速度远超于质心算法，这是由于信标节点数随节点总数的增加而增加的原因，说明未知节点的数量对本文算法的影响微乎其微。图中DV-Hop算法的定位误差曲线无太大波动，说明在信标节点比例一定时，DV-Hop算法的定位精度受节点总数变化的影响不明显，这与该算法的性质有关。

图7(c)表示在网络规模以50 m为间隔从300 m(长、宽、高均为300 m)扩大至450 m的情况下本文算法与另两种传统定位算法的定位误差对比图。由图可得，网络规模对本文算法的定位精度有一定影响，网络规模越小定位精度就越高。即使在网络规模较大(网络规模为450 m×450 m×450 m)的情况下，相较于另两种算法的误差值(DV-Hop:约0.3，Centroid:约0.33)，本文算法仍具有较低的定位误差值，约为0.23。

图7 3种变量对平均定位误差的影响

仿真结果表明，本文算法在通信开销小于或大致相同于另两种定位算法的情况下，在多种影响因素下均具有较高的定位精度，与传统定位算法相比其定位精度最大可提高约23%。

5 结语

本文提出一种面向非完全序列的水下三维传感网定位算法。利用3D Voronoi图对定位空间进行区域划分，将划分后得到的Voronoi子区域边的中心、面的中心与体的中心作为虚拟信标节点并得到其阶次序列，比较由RSSI得到的未知节点序列与信标节点序列的阶次相关系数并构建最邻近序列表，最终，利用改进后的RSD算法计算未知节点序列(非完全序列)与对应的最邻近序列表中各序列(全序列)的阶次相关系数，将该系数作为权重并结合对应节点坐标实现对未知节点位置的加权估计。仿真结果表明，在不增加任何硬件的情况下，本文算法有效提高了定位精度，与传统定位算法相比定位精度最大可提高约23%。

References)

[1] DU X D, JI J T, YAN D P. Application research of wireless sensor network in intelligent transportation system [J]. Advanced Materials Research, 2010, 108/109/110/111: 1170-1175.

[2] LIU L, WU X, ZHU Z, et al. A localization algorithm based on beacon error problem in underwater wireless sensor network [C]// Proceedings of the 15th IEEE International Conference on Communication Technology. Piscataway, NJ: IEEE, 2013: 478-482.

[3] WALDMEVER M, TAN H P, SEAH W K G. Multi-stage AUV-aided localization for underwater wireless sensor networks [C]// Proceedings of the 25th IEEE International Conference on Advanced Information Networking and Applications Workshops. Washington, DC: IEEE Computer Society, 2011: 908-913.

[4] BAHL P, PADMANABHAN V N. RADAR: an in-building RF-based user location and tracking system [C]// Proceedings of the 19th Annual Joint Conference of the IEEE Computer and Communications Societies. Piscataway, NJ: IEEE, 2000: 775-784.

[5] 肖竹,谭光华,李仁发,等.无线传感器网络中基于超宽带的TOA/AOA联合定位研究[J].计算机研究与发展,2013,50(3):453-460.(XIAO Z, TAN G H, LI R F, et al. Joint TOA/AOA localization based on UWB for wireless sensor networks [J]. Journal of Computer Research and Development, 2013, 50(3): 453-460.)

[6] 吴绍华，张钦宇，张乃通.UWB无线传感器网络中基于匹配滤波检测的TOA估计[J].软件学报,2009,20(11):3010-3022.(WU S H, ZHANG Q Y, ZHANG N T. TOA estimation based on match-filtering detection for UWB wireless sensor networks [J]. Journal of Software, 2009, 20(11): 3010-3022.)

[7] 陈鸿龙，李鸿斌，王智.基于TDoA测距的传感器网络安全定位研究[J].通信学报,2008,29(8):11-21.(CHEN H L, LI H B, WANG Z. Research on TDOA-based secure localization for wireless sensor networks [J]. Journal on Communications, 2008, 29(8): 11-21.)

[8] ADEMUWAGUN A, FABIO V. Reach centroid localization algorithm [J]. Wireless Sensor Network, 2017, 9: 87-101.

[9] HOSSEINIRAD S M, POURDEILAMI J, NIAZI M, et al. On improving APIT algorithm for better localization in WSN [J]. Journal of AI & Data Mining, 2013, 2(2): 97-104.

[10] ZHANG A, YE X, HU H, et al. Improved DV-HOP positioning algorithm based on one-hop subdivision and average hopping distance modification [J]. Chinese Journal of Scientific Instrument, 2012, 33(11): 2552-2559.

[11] YEDAVALLI K, KRISHNAMACHARI B. Sequence-based localization in wireless sensor networks [J]. IEEE Transactions on Mobile Computing, 2007, 7(1): 81-94.

[12] 刘志华,陈嘉兴,陈霄凯.无线传感器网络中序列定位新算法的研究[J].电子学报,2010,38(7):1552-1556.(LIU Z H, CHEN J X, CHEN X K. A new algorithm research of sequence-based localization technology in wireless sensor networks [J]. Acta Electronica Sinica, 2010, 38(7): 1552-1556.)

[13] 裴忠民,邓志东,徐硕,等.一种基于N-最优阶次序列的无线传感器网络节点定位方法[J].自动化学报,2010,36(2):199-207.(PEI Z M, DENG Z D, XU S, et al. A new localization method for wireless sensor network nodes based onN-best rank sequence [J]. Acta Automatica Sinica, 2010, 36(2): 199-207.)

[14] 刘影,钱志鸿,孙大洋.基于参考点序列的无线传感器网络节点定位算法[J].吉林大学学报(工学版),2012,42(2):489-493.(LIU Y, QIAN Z H, SUN D Y. Node localization scheme for wireless sensor networks based on reference node sequence [J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(2): 489-493.)

[15] LIU J, YAN F, YANG X. 3D localization algorithm based on Voronoi diagram and rank sequence in wireless sensor network [J]. Scientific Programming, 2017, 2017(4): Article No. 4.

[16] ZHONG Z, HE T. RSD: a metric for achieving range-free localization beyond connectivity [J]. IEEE Transactions on Parallel & Distributed Systems, 2011, 22(11): 1943-1951.

[17] ALMASHOR M, KHALIL I. Reducing network load in large-scale, peer-to-peer virtual environments with 3D Voronoi diagrams [C]// Proceedings of the 17th International Conference on High Performance Computing. Washington, DC: IEEE Computer Society, 2010: 1-10.

[18] HWANG G J, ARUL J M, LIN E, et al. Design and multithreading implementation of the wave-front algorithm for constructing Voronoi diagrams [C]// ICA3PP: Proceedings of the 6th International Conference on Algorithms and Architectures for Parallel Processing. Berlin: Springer, 2005: 257-266.

[19] LIU J Y, LIU S. A survey on applications of Voronoi diagrams [J]. Journal of Engineering Graphics, 2004, 25(2): 125-132.

[20] DU Q, GUNZBURGER M, JU L L. Advances in studies and applications of centroidal Voronoi tessellations [J]. Numerical Mathematics: Theory, Methods and Applications, 2010, 3(2): 119-142.

[21] 陈嘉兴,刘志华.无线传感器网络节点的三维序列内心定位算法[J].南京理工大学学报(自然科学版),2011, 35(3): 371-375.(CHEN J X, LIU Z H. 3D Sequences and incenters localization algorithm for nodes in WSN [J]. Journal of Nanjing University of Science & Technology, 2011, 35(3): 371-375.)

[22] 胡敏.基于阶次序列加权的无线传感器定位算法[J].计算机工程与应用,2014,50(10):116-119.(HU M. Node localization algorithm of wireless sensor networks based on optimal weighted rank sequences [J]. Computer Engineering and Applications, 2014, 50(10): 116-119.)

[23] YANG X, LIU J. Sequence localization algorithm based on 3D Voronoi diagram in wireless sensor network [J]. Applied Mechanics & Materials, 2014, 644-650: 4422-4426.

This work is partially supported by the National Key Research and Development Program of China (2016YFC060908), the National Natural Science Foundation of China (51674255), the Production-Study-Research Joint Prospective Research Project of Jiangsu Province (BY2014028- 09).

CHEDi, born in 1994, M. S. candidate. Her research interests include sensor network, ocean observing network.

NIUQiang, born in 1974, Ph. D., professor. His research interests include machine learning, data mining.