移动机会网络中一种轻量级的分布式社会距离路由算法
2018-03-20袁培燕宋明阳
袁培燕,宋明阳
(河南师范大学 计算机与信息工程学院,河南 新乡 453007)(*通信作者电子邮箱peiyan@htu.cn)
0 引言
随着短距离无线通信以及传感器技术的飞速发展,目前的智能移动设备,如智能手机、平板电脑和笔记本电脑拥有了强大的移动通信与数据感知功能。利用这些设备组成的移动机会网络可以通过使用本地无线链路来进行复杂情况下的自组织通信。目前,移动机会网络不仅支持新兴的应用,比如移动电子商务服务、灾难搜救服务以及移动社交服务,也支持传统的服务,如内容分发、万维网应用等。不同于存在端到端数据传输路径的传统无线传感网络或自组织网络。在移动机会网络中,数据包的源节点和目的节点之间不存在可靠的端到端路径,数据包的传输依赖于节点的移动性和机会性接触,并以“存储、携带、转发”的模式工作[1],因此,如何在链路间歇性连接的情况下有效地传输数据是移动机会网络面临的一大挑战。洪泛[2]是最早提出的一种机会路由算法。它通过向网络中扩散数据包的备份的方式(每当两个节点相遇时它们都会将自己的数据包的备份复制给对方)来将数据包投递至其目的节点,该方式并不需要复杂的路由决策(当两节点相遇时判断将数据包发送给对方是否对该数据包到达其目的节点具有正面影响)。洪泛算法虽然拥有最优的包的投递率和投递延迟性能,但由于网络中存在较多的数据包备份,因此传输代价也较高。研究人员提出了一些更为智能化的方案来改善洪泛的高负载问题。这些方案可以分为两类:基于节点接触信息的路由策略和基于节点社会关系信息的路由策略。基于节点接触信息的路由通常利用节点间接触概率、历史接触记录、接触位置和次数以及节点间运动相似度来帮助路由决策。基于节点社会关系的路由通常将数据包投递至具有较高中心性的节点或选择与数据包目的节点具有相似性(兴趣、上下文、朋友、社区)的中继节点。上述两类路由算法的共同点在于它们使用了额外信息(接触信息、社会信息)来为数据包选择具有更高转发效率的中继节点。这些运用到额外信息(本文称之为辅助信息)帮助数据包转发的路由策略统称为信息辅助型路由算法[3]。信息辅助型路由策略虽然解决了洪泛路由由于过多的数据包备份而造成的网络开销过大问题,但是节点之间的辅助信息的共享方式依然采用类似于洪泛的方式进行(每当两个节点接触时会交换并更新彼此的辅助信息)。这样会造成两方面的网络开销:首先,网络中节点每进行一次辅助信息的交换会浪费电量与带宽;其次,过多的辅助信息会占用设备有限的存储空间。由此可见,传统的辅助信息型路由算法在大型的移动机会网络中依然会造成较大的网络开销。
针对此问题,本文提出一种结合节点接触信息与社会关系的轻量级分布式社会距离机会路由算法。该算法首先通过分析节点间接触的稳定性与规律性来确立节点间的朋友关系,然后利用朋友关系来构建出节点之间的关系亲疏程度(亲密和疏远的程度)。如图1所示,该图描述了一个拥有8个节点的小型机会网络在某时刻内节点间接触以及朋友关系。从图中可以看出,节点之间虽然不能两两互为朋友,但是可以通过朋友节点之间多跳传输完成数据投递。本文使用社会距离来量化节点之间的朋友关系。以节点a为例,a与b为朋友,它们的社会距离为1,而a与b的朋友d和e的距离则为2,依此类推。由于朋友节点之间接触频繁且有规律,因此由朋友关系所构成的节点间社会距离越短则代表节点间关系越密切。当a中有一个目的节点为g的数据包并且a与d接触时,由于d与g的社会距离更短,d具有更大的几率遇到g,所以a将数据包发送给d。总之,与包的目的节点社会距离越短的节点,其投递该包效率也就越高。
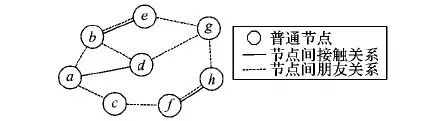
图1 节点间社会距离示例
此外社会距离的建立并不需要通过所有节点进行洪泛式的信息交换来完成,只需要通过朋友节点之间进行信息交换和共享即可。由于所有节点并不能两两建立朋友关系,所以信息的共享仅发生在有限的节点对之间,因此可以大量减少信息的交换次数。
本文的贡献如下:1)通过分析节点间的接触规律性与稳定性提出了一种节点间朋友关系识别方法,为机会网络中节点之间的社会性研究提供了新的依据。2)在朋友关系的基础上,提出了一种轻量级的分布式距离向量机会路由算法,节点之间通过有选择地信息共享方式来构建节点间社会距离,并以此作为辅助信息来协助路由决策。
实验结果显示,该算法与经典的辅助信息型路由算法在投递率、包传输延时指标有所提升的前提下,辅助信息的交换次数大幅减少,节省了网络资源。
1 相关工作
利用一些额外的信息协助节点进行数据包转发决策是当前机会网络路由算法研究的重点之一。下面来介绍一些相关的工作。
基于节点接触信息的路由策略:文献[4]根据节点间的接触次数以及接触时长,提出了利用接触和传输记录的概率路由(Probabilistic Routing Protocol using History of Encounters and Transitivity, PRoPHET)算法。PRoPHET通过记录并分析接触历史记录来计算节点之间的接触概率,当两个节点发生接触时,它们的接触概率相应增加,而当它们经过一段时间没有发生接触时,接触概率相应下降。文献[5]提出了一种结合喷雾—等待策略并考虑到缓冲区管理的多备份概率路由。文献[6]提出了利用直接接触的节点和两跳邻居节点的历史接触信息计算接触概率的改进型概率路由。文献[7]结合节点间最大相遇次数、数据包最大化投递概率以及最小化目标节点的距离等三个指标提出了多目标函数,并将该函数优化后作为数据包的路由转发的依据。文献[8]提出了一种基于数据包传递概率机会路由算法,其中数据包的传递概率的计算结合了节点的接触频率以及接触持续时间。
基于节点社会关系信息的路由策略:文献[9]提出利用节点的接触频率、平均接触时长、接触的规律性来识别节点的社会关系。文献[10]利用邻居节点的接触信息,分布式地估计节点的中心度和相似度,并融合二者提出基于中心度与相似度的路由(routing based on Betweenness centrality and Similarity, SimBet)算法。当两个节点相遇时,需要交换各自邻域知识,计算中心度和相似度,然后将数据包转发给效用值较高的节点。此外,文献[11]提出了经典的人群排名(PeopleRank)路由算法分布式地计算节点的中心度,降低了传统社会化网络分析方法计算节点中心度的算法复杂度,取得了比较好的效果。文献[12]提出以模糊推理方法来对节点位置相似性以及社会相似性信息进行处理来得到辅助信息,并以此作为数据包转发的依据。文献[13]首先通过分析网络中节点的实时数据来提取影响节点间社会关系的因素;然后对这些因素的复杂性和动态性进行推理和评估,并从其中计算出每个节点的社会关系值;最后基于社会关系值来建立邻居节点的拓扑信息来为数据包选择下一跳中继节点。
上述类型的信息辅助型路由算法所关注的是数据包的转发问题。然而,对于从减少节点间辅助信息交换次数的角度来提升路由算法的性能,据作者所知尚无相关工作。而本文则围绕这一问题进行讨论,并提出了分布式社会距离机会路由算法,致力于在保证数据包转发效率基础上减少辅助信息的交换次数。
2 路由算法设计
在以往的机会路由算法中辅助信息的交换与共享是所有节点共同参与的,然而,这将消耗大量的网络带宽与存储资源(当信息交换时,接收方首先需要存储接收到的信息;然后更新自己的辅助信息;最后将收到的信息删除,但是在删除之前,即时性保存接收到信息的依然会占用存储空间,进而导致影响数据包的接收与存储。在本文的方法中由于减少了信息的交换次数,因此有大量的节点无需进行临时信息的存储,减少了存储资源的浪费),因此在设计路由算法时应当考虑减少过多的信息交换。此外,在减少信息交换的前提下,应该保证信息共享的高效性与正确性;否则,错误的辅助信息会引导数据包到一条较差的路径,进而影响到路由性能(投递率与投递延时)。下面来介绍本文的解决方案。
2.1 节点间朋友关系识别
信息的高效共享依赖于节点之间是否拥有紧密的联系,但是与传统强连通自组织网络中显性的节点关系不同,移动机会网络中,节点的接触情况是时变的、复杂的。有的节点对频繁接触,有的偶尔接触,有的接触时间长,有的间隔时间长。节点之间呈现一种动态变化的连接方式。针对这种连接方式,本文联合节点接触情况的稳定性、规律性来判别节点的朋友关系:如果一对节点在接触时长和接触时间间隔方面有较高的稳定性和较好的规律性,则将它们定义为朋友。通过识别节点的朋友关系,一方面可以将机会网络中具有紧密关系的节点对更清晰地刻画出来,另一方面辅助信息在朋友节点之间可以更高效地共享。
本文观察两节点在时间段内的接触总时长的长短来判断节点间的接触稳定性。图2描述了a,b∈V两节点在19 s的时间段内的两种接触情况。通过对比可以发现,在图2(b)所描述的接触情况中a、b两节点的总接触时间(16 s)远远大于图2(a)(8 s),并且在接触间隔时间方面前者也远远小于后者。如果节点之间每隔固定时间(比如1 s)进行一次信息交换与更新的话,那么在时间段内节点间接触时间越多(图2(b))则越能保证信息更新的实时性与正确性。如果节点间接触间隔时间越长(图2(a)),则节点间的信息更新将会受到较大的影响(间隔时间内节点间无法进行信息更新)而导致信息陈旧与无法保证信息更新实时性。因此本文对机会网络中节点间接触的稳定性描述为:在时间段内,如果两个节点的平均接触时长较大(对于节点a来说则是大于该节点与其所有接触过的节点的平均接触时间,节点b同理),则说明这两个节点的接触是稳定的。
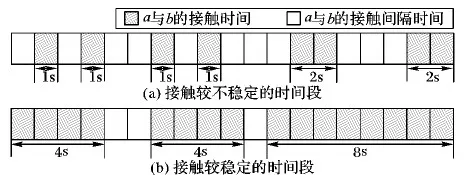
图2 节点间接触稳定性
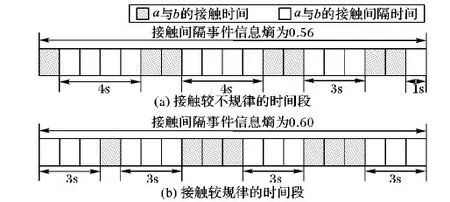
图3 节点间接触规律性
2.2 节点间社会距离
在社交网络中,节点(手持移动设备的人)通常会较为频繁地、有规律地与其熟悉的节点相遇,如在一起工作和学习的同事、同学、朋友或家人等。这些相互熟悉的节点在数据转发中扮演了重要的角色[14]。通常这些节点之间具有最为紧密的社会关系。而在以人为本的机会网络中,如果可以充分利用熟悉的节点之间的紧密关系,则可以确定出机会网络中节点之间的社会关系的紧密程度。在本文中,首先定义具有最高紧密度社会关系的节点对互为朋友节点(朋友关系)。然后联系朋友关系,将节点之间社会关系的紧密程度用社会距离来量化。社会距离越大则代表两节点的社会关系越疏远;反之越紧密。
2.2.1 朋友节点间接触时社会距离的构建
假设机会网络G(V)中的任意节点a∈V维护了一张社会距离表用来记录与其他节点的社会距离。表的每一行代表一个条目,每个条目中包括三个项:①需要计算社会距离的目的节点;②社会距离;③该条目的来源节点ID。节点的社会距离表的构建主要分为以下步骤:
1)当两节点被检测互为朋友时,其将对方的相关信息加入到社会距离表中:以节点a为例,在T0时刻a与节点b被识别为朋友关系(如图4(a)所示)。然后a将节点b的相关信息作为条目插入到表中,由于两节点互为朋友,所以a与b的社会距离项为最小值1,并且该条目的来源节点项与目的节点项一致为b(如图5(a)所示)。由于a、b两节点是由相互接触而识别对方为朋友关系并将对方的信息记录在表中,因此在上述步骤中并没有发生信息的交换。
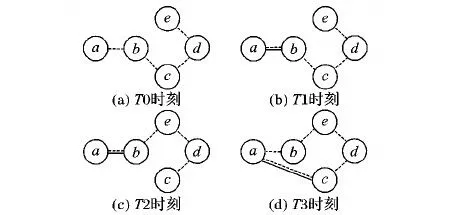
图4 机会网络朋友关系以及接触的变化示例
2)当两节点在互为朋友的基础上接触时交换并更新各自的社会距离表:在T1时刻,a与b在互为朋友的情况下相互接触(如图4(b)所示)。首先a获取b的表中记录的关于目的节点c、d、e的条目,由于在a的表中不存在关于目的节点c、d、e的条目,因此a将这些获取到的条目中的社会距离项+1并将来源节点项设置为b之后直接插入到表中(如图5(b)所示)。
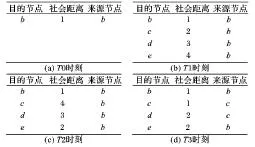
图5 节点a的社会距离表变化情况(对照图4)
3)当获取到的新条目与表中已存在的条目中的目的节点项相同时,则分以下两种情况进行更新:
①已有条目的来源节点项与新条目来源节点相同时,无条件使用新条目更新已有条目:如图4(c)所示,在T2时刻b、c的朋友关系断开,b、e互为朋友关系,并且b的社会距离表完成了更新。此时a与b在互为朋友的情况下相互接触后,a获取b的表中关于目的节点c、d、e的条目,将社会距离项+1并将来源节点项设置为b之后直接覆盖更新相应的原有条目(如图5(c)所示)。
②已有条目的来源节点项与新条目的来源节点不同时则比较它们的社会距离,如果新条目的社会距离+1仍小于已有条目的社会距离,则使用新条目更新已有条目:如图4(d)所示,在T3时刻,a、c在互为朋友的基础上进行接触并且a获取节点c中关于目的节点d、e的条目。通过对比发现,从节点c获取的关于目的节点d的条目的社会距离项+1小于表中已有的条目(2<3),因此将新的条目社会距离项+1且来源节点项设置为c后覆盖更新旧的条目。然而从c获取的关于目的节点e的条目的社会距离项+1大于表中已有的相应的条目(3>2),因此保留原表项不进行更新(如图5(d)所示)。
上述是节点a与其朋友节点接触之后社会距离表的更新过程。同样的,a的朋友节点也会采取同样的策略来进行表的更新。上述过程中,一个节点获取另一个节点的信息(条目),本文称之为一次辅助信息的交换。相比传统机会路由算法中洪泛式的信息交换策略,在该算法中由于节点间在接触的基础上互为朋友才交换信息,并且节点间并非两两互为朋友,因此该算法可以减少大量的信息交换次数。
2.2.2 朋友关系断开时社会距离的更新
当两节点的朋友关系断开时,为了保证社会距离表能够正确更新,令节点将以对方为来源节点的条目中社会距离设置为无穷大,并且将这些条目扩散至其接触到的其他的朋友节点。这样一来其他节点能迅速得知周围节点的社会距离变化情况。如图6所示,a与d的朋友关系在某时刻内断开,此时,a会将自己表中来源节点为d的条目的社会距离设置为无穷大(如图7(a)所示)。当a与其朋友节点b接触时,a将社会距离被设置为无穷大的条目发送至其朋友节点b,b则无条件根据接收到条目来更新对应旧的条目(如图7(b)所示)。对于节点d而言也会重复同样的操作进行更新。
图6 节点a与d的朋友关系断开
Fig. 6 Breaking up of friend relationship between nodeaandb

图7 朋友关系断开后节点a与b的表的更新(对照图6)
2.2.3 环路更新问题及解决
然而上述的更新规则会产生环路问题。如图8(a)所示,在T0时刻,a与c的朋友关系断开,a将自己表中来源节点为c的条目设置为无穷大,而在b中存有通过节点a更新的关于节点c的条目(目的节点为c、来源节点为a、社会距离为2)。在T1时刻如果节点b首先将该条目发送给a,那么根据上述的信息更新规则,a无条件根据新的条目更新旧的条目,这样导致了a更新了错误的关于节点c的条目(目的节点为c、来源节点为b、社会距离为3)。在T2时刻,a又会将错误的条目继续发送给b。依此循环,两节点始终更新的是错误的条目。产生这种错误的原因在于:b在收到a的条目并使用其更新自己的条目之后,b又将通过a更新过的条目发回给了节点a,这样造成了a的错误更新,并在后续的时间里a与b交换错误的条目造成了环路更新。
如果b不将通过a更新的条目发回给节点a,则可以避免a进行错误的更新,进而避免a、b进行环路更新。如图8(b)所示,在T1时刻,b拒绝将条目(目的节点为c、来源节点为a、社会距离为2)发送给a。在T2时刻,b接收a发送的关于节点c的条目(目的节点为c、来源节点为a、社会距离为∞)并且通过新收到的条目将自己的关于节点c的条目进行更新(目的节点为c、来源节点为a、社会距离为∞),至此a、b完成了正确的更新。
综上所述,对于节点的社会距离表中的每一个条目来说,令其不能更新其来源节点的社会距离表,则可以解决节点之间的环路更新问题。
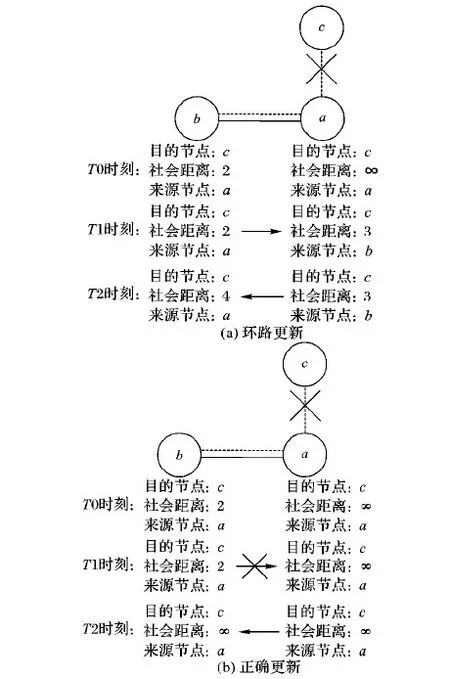
图8 环路更新问题
2.2.4 节点间社会距离构建流程
在这里给出了节点间社会距离的计算流程,大致如下:
1)首先识别节点间的朋友关系(2.1节)。
2)检测节点间朋友关系是否有断开情况(如果在上个时间段内两节点被判定为朋友,而在目前时间段内不为朋友,则可以判定两节点的朋友关系断开)。如果断开的话则根据2.2.2节的规则进行社会距离表的更新。这样的好处在于节点能够在第一时间内发现朋友关系的断开情况,并且在后续的社会距离构建过程中可以这些把断开情况通知给其他接触到的朋友节点,以便让这些节点能够及时感知到与其他节点的社会距离变化情况,避免错误的更新。
3)当朋友节点之间接触时根据2.2.1节的规则进行社会距离表的构建。需要注意的是,在更新的过程中对于表中的任意条目而言,不能用于更新其来源节点的社会距离表,以防出现环路更新问题(如2.2.3节所述)。
4)每当节点间进行一次社会距离表的交换时,记录一次信息交换次数,以便和传统的辅助信息路由算法进行对比。社会距离的详细构建流程已写成伪码,如算法1所示。
算法1 节点间社会距离构建流程。
输入:机会网络节点集合V。
输出:辅助信息交换次数。
1)
FOR 任意节点a,b∈VDO
2)
IFa与b的邻居关系断开 THEN
3)
FORa中的社会距离表中的任意条目ENaDO
4)
IFENa的来源节点为bTHEN
5)
ENa的社会距离=∞
6)
END IF
7)
END FOR
8)
END IF
9)
IFa与b互为邻居关系 ANDa与b接触 THEN
10)
a获取b的社会距离表,辅助信息交换次数++
11)
FORa获取的b的社会距离表中的任意条目ENbDO
12)
ENexist← false
13)
FORa中的社会距离表中的任意条目ENaDO
14)
IFENb的目的节点项==ENa的目的节点项ANDENb的来源节点项!=aTHEN
15)
ENexist← true
16)
IFENa的来源节点项==bTHEN
17)
ENa的社会距离项=ENb的社会距离项+1 ANDENa的来源节点项=b
18)
ELSE IFENb的社会距离+1 19) ENa的社会距离项=ENb的社会距离项+1 ANDENa的来源节点项=b 20) END IF 21) END IF 22) IFENexist=false THEN 23) ENb的社会距离项+1,来源节点项设置为b 24) 将ENb插入a的社会距离表 25) END IF 26) END FOR 27) END FOR 28) a完成社会距离表更新并删除获取到的社会距离表 29) END IF 30) END FOR 31) RETURN 辅助信息交换次数 算法1)~8)行判断a和b两节点在当前时间段内是否断开,如果是则a将自己表中来源节点为b的条目中社会距离项设置为无穷大。算法9)~10)行判断节点a与b是否在互为朋友的情况下相互接触,如果是则a获取b的社会距离表并记录一次信息交换次数。算法11)~21)行a将获取到的b的社会距离表中的任意条目ENb和a的社会距离表中的任意条目ENa进行对比。如果ENb与ENa的目的节点项相同并且ENb的来源节点不是a(这里保证社会距离构建时不产生环路),则满足信息更新条件:如果ENa的来源节点项为b,则ENa的社会距离项被ENb的社会距离项+1赋值,来源节点项设置为b(算法16)~17)行);否则如果ENb的社会距离+1小于ENa的社会距离那么执行与算法17)行相同操作。算法22)~27)行,如果a的社会距离表中不存在与ENb具有相同目的节点项的条目,则将ENb的社会距离项+1且来源节点项设置为b,然后将该项插入到自己的社会距离表中。算法28)~31)行,当a完成社会距离表的更新后删除获取到的b的社会距离表释放空间。最后返回信息的交换次数。 在路由决策(数据包传递)方面,节点总是将数据包发送到距离其目的节点社会距离最短的节点。如图1所示,以节点a为例,a中携带有一个目的节点为g的数据包,当a与d接触时,通过判断d与g的社会距离小于a与g,因此,a将数据包发送给d。由d携带该数据包将会更高效地将其发送到其目的节点g。 下面总结了分布式社会距离路由算法并给出了伪码,如算法2所示。 算法2 分布式社会距离机会路由算法。 1) 根据邻居发现算法计算节点间邻居关系 2) 检测邻居关系断开情况并进行节点内社会距离表的更新 3) FOR 任意节点a,b∈VDO 4) IFa与b接触 THEN 5) IFa与b互为邻居 THEN 6) 交换并更新各自的社会距离表 7) END IF 8) FOR 在a的缓冲区中的任意数据包PKaDO 9) IFPKa的备份不存在于b的缓冲区中 THEN 10) IFa和b的社会距离表中都存在有目的节点项为PKa的目的节点的条目(分别为ENa和ENb) THEN 11) IFENa的社会距离>ENb的社会距离 THEN 12) a转发PKa的备份至b 13) END IF 14) END IF 15) END IF 16) END FOR 17) b接收a转发的包的备份 18) END IF 19) END FOR 算法1)~2)行首先通过朋友发现算法确定节点间朋友关系,检测节点间朋友关系是否有断开情况并进行相应的社会距离表的更新。算法3)~7)行对于任意节点a和b判断是否互为朋友并且相互接触,如果满足则交换并更新社会距离表。算法8)~16)行对于在a的缓冲区中的任意数据包PKa,如果该包的备份不存在于b的缓冲区内,并且a与b的社会距离表中都存在有目的节点项为PKa的目的节点的条目,其分别为ENa和ENb,那么比较ENa与ENb的社会距离,如果前者大于后者则证明b到PKa的目的节点的社会距离小于a,因此a将包PKa转发给b。算法17)~19)行节点b接收a转发的包的备份。算法结束。 下面对辅助信息的交换次数进行量化分析。将两节点相互接触设为随机事件C,互为朋友设为随机事件F,那么两事件发生的概率分别为P(C)和P(F)。在传统的机会路由算法中辅助信息的交换概率为P(C),因为当两节点接触时就交换辅助信息。下面分两种情况进行讨论:当两事件为独立事件,在社会距离路由算法中交换辅助信息的概率为P(C∩N)=P(C)*P(N),即两节点同时相互接触并且互为朋友的概率。设P(C)与P(N)分别为0.5与0.4,那么P(C∩N)=0.2 本文对所提出的社会距离路由算法在Visual C++ 6.0平台上面进行了集成,并以经典的辅助信息路由算法——PRoPHET算法(基于接触信息的路由)与SimBet算法(基于社会信息的路由)进行性能上的对比与分析。实验场景如下:节点间最大通信距离为25 m,每隔1 s搜索一次邻居(接触关系)节点,仿真时间为15 000 s。采用的真实节点移动数据集来源于韩国科学技术院(Korea Advanced Institute of Science and Technology, KAIST),其记录了大学校园内人群的日常活动行为轨迹。共有34人参与到数据的收集过程,每人手持全球定位系统(Global Positioning System, GPS)设备收集其92天的日常移动轨迹,关于该数据集的具体细节可以在文献[15]中查阅。本文使用3个指标来评价路由算法的性能: 1)投递率。网络中被成功接收的包的数量和产生的包的数量的比值,其代表了网络中包可以被成功投递到目的节点的比率。 2)包传输延时。网络中所有到达目的地的包从产生到传输至目的节点所需的时间的平均值。 3)辅助信息交换次数。网络中所有节点通过其他节点获取辅助信息的总次数。 图9~11分别展示了3种算法在投递率、延时以及辅助信息交换次数的对比。对于投递率方面,如图9所示,从整体上来看,社会距离算法要高于PRoPHET与SimBet约0.6左右。而在仿真时间的初期(也就是0~2 800 s时)社会距离算法的投递率略低,这是因为在算法执行的初期,由于节点间接触次数有限,导致了节点的社会距离表更新的不完整,使用不完整的社会距离会导致将包引入较差的路径,进而导致投递率较低,但是随着社会距离表的更新完整,数据包可以被正确的辅助信息来引导入一条较高的转发效率的路径。对于包传输延时方面,如图10所示,在仿真时间0~4 200 s时社会距离算法要高于PRoPHET与SimBet,而在4 200 s到仿真时间结束时,传输延时则逐渐降低,平均降低250 ms。其原因与投递率类似:由于仿真前期社会距离表的不完整,导致包的投递效率不高,投递一个包需要花费较多的时间;随着社会距离表的更新趋于完善,包的投递效率上升,进而投递数据包需要花费的时间减少,延时因此下降。 图9 投递率指标对比 对于辅助信息的交换总次数,从图11可以看出,从仿真时间开始社会距离算法就远远低于PRoPHET与SimBet,并且随着时间的推移,社会距离算法辅助信息交换次数的涨幅也远远低于洪范机制,在仿真时间的最后,PRoPHET与SimBet的交换次数约在76万次左右,而选择性移交机制则只有28万次左右,增益超过63%。其原因如下:对于PRoPHET而言,每当两节点接触时需要通过获取对方节点中对于其他节点的接触概率来计算接触概率的传递性。而对于SimBet而言,当两节点相遇时,需要交换各自的邻域知识来计算中心度与相似度。上述两种算法的辅助信息的交换是洪泛式的,也就是说,节点间的接触总次数即是信息的交换次数。而对于社会距离路由算法来说,辅助信息(社会距离表)的交换是节点间在互为朋友的基础上进行的,而机会网络中节点间的朋友个数是有限的,因此朋友间的接触次数即是信息的交换次数。对比与洪泛式的信息交换策略,该方式明显可以减少大量信息交换。 图10 包传输延时指标对比 图11 辅助信息交换次数对比 本文针对信息辅助型机会路由算法的洪泛式信息交换方式所造成的网络资源浪费问题,提出了分布式的社会距离路由算法。首先通过分析机会网络中节点间接触的规律性和稳定性提出了机会网络中朋友关系识别算法。然后联合朋友关系确定出节点间亲疏度关系并用社会距离来量化。一方面,辅助信息限于朋友节点间进行交换与共享,减少了信息的交换次数。另一方面,数据包交付给与其目的节点社会距离较短的节点来携带,可以提高数据包的投递效率。最后实验结果证明了算法的有效性。未来的工作是基于该路由算法考虑缓冲区管理策略,以便进一步优化该算法的性能。 References) [1] YUAN P, FAN L, LIU P, et al. Recent progress in routing protocols of mobile opportunistic networks [J]. Journal of Network & Computer Applications, 2016, 62: 163-170. [2] VAHDAT A, BECKER D. Epidemic routing for partially-connected Ad Hoc networks, technical report CS- 200006 [R]. Durham: Duke University, 2000: 5. [3] 马华东,袁培燕,赵东.移动机会网络路由问题研究进展[J].软件学报,2015,26(3):600-616.(MA H D, YUAN P Y, ZHAO D. Research progress on routing problem in mobile opportunistic networks [J]. Journal of Software, 2015, 26(3): 600-616.) [4] LINDGREN A, DORIA A, SCHELÉN O, et al. Probabilistic routing in intermittently connected networks [J]. ACM SIGMOBILE Mobile Computing & Communications Review, 2004, 7(3): 239-254. [5] LI Z, SHEN H. Probabilistic routing with multi-copies in delay tolerant networks [C]// Proceedings of the 2008 International Conference on Distributed Computing Systems Workshops. Piscataway, NJ: IEEE, 2008: 471-476. [6] WANG X, HE R, LIN B, et al. Probabilistic routing based on two-hop information in delay/disruption tolerant networks [J]. Journal of Electrical & Computer Engineering, 2015, 2015(3): Article No. 9. [7] BORAH S J, DHURANDHER S K, WOUNGANG I, et al. A multi-objectives based technique for optimized routing in opportunistic networks [J]. Journal of Ambient Intelligence & Humanized Computing, 2017, 2017(1): 1-12. [8] YU C, TU Z, YAO D, et al. Probabilistic routing algorithm based on contact duration and message redundancy in delay tolerant network [J]. International Journal of Communication Systems, 2016, 29(16): 2416-2426. [9] BULUT E, SZYMANSKI B K. Exploiting friendship relations for efficient routing in mobile social networks [J]. IEEE Transactions on Parallel & Distributed Systems, 2012, 23(12): 2254-2265. [10] DALY E M, HAAHR M. Social network analysis for routing in disconnected delay-tolerant MANETs [C]// Proceedings of the 2007 International Symposium on Mobile Ad Hoc Networking and Computing. New York: ACM, 2007: 32-40. [11] MTIBAA A, MAY M, DIOT C, et al. PeopleRank: social opportunistic forwarding [C]// Proceedings of the 2010 Conference on Information Communications. Piscataway, NJ: IEEE, 2010: 111-115. [12] JANG K, LEE J, KIM S K, et al. An adaptive routing algorithm considering position and social similarities in an opportunistic network [J]. Wireless Networks, 2016, 22(5): 1537-1551. [13] WU X H, GU X F, POSLAD S. Routing algorithm based on social relations in opportunistic networks [C]// Proceedings of the 2015 International Computer Conference on Wavelet Active Media Technology and Information Processing. Piscataway, NJ: IEEE, 2015: 146-149. [14] CHAINTREAU A, HUI P, CROWCROFT J, et al. Impact of human mobility on the design of opportunistic forwarding algorithms [C]// Proceedings of the 2006 International Conference on Computer Communications. Piscataway, NJ: IEEE, 2006: 1-13. [15] RHEE I, SHIN M, HONG S, et al. On the levy-walk nature of human mobility [J]. IEEE/ACM Transactions on Networking, 2011, 19(3): 630-643. This work is partially supported by by the National Natural Science Foundation of China (U1404602), the Science and Technology Foundation of Henan Province (172102210341), the Young Scholar Program of Henan Province (2015GGJS086), the Doctoral Research Startup Project of Henan Normal University (qd14136), the Young Scholar Program of Henan Normal University (15018). YUANPeiyan, born in 1978, Ph. D., associate professor. His research interests include mobile communication and group intelligence computation. SONGMingyang, born in 1991, M. S. candidate. His research interests include mobile opportunity network.2.3 分布式社会距离路由算法
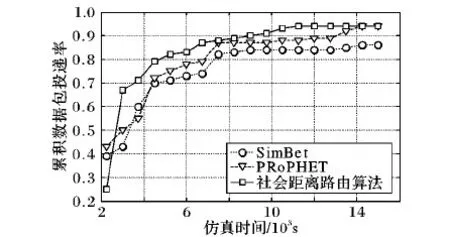
3 实验结果与分析
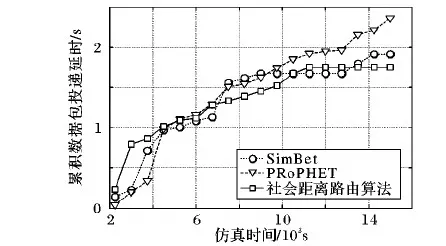

4 结语
