基于多块结构重叠网格的电磁轨道发射器动态发射过程流场分析

杜佩佩， 鲁军勇， 冯军红， 李湘平

(海军工程大学 舰船综合电力技术国防科技重点实验室, 湖北 武汉 430033)

0 引言

电磁轨道发射器动态发射过程，依靠作用于电枢洛伦兹力推动弹丸运动。目前一些学者[1-5]在研究中忽略气动阻力影响，基于电磁力和电枢与导轨接触产生摩擦力，建立弹丸动态发射过程内弹道模型。试验表明：电磁轨道发射器弹丸受到电磁推力在106N量级；数值仿真和经验公式计算表明，钝头体弹丸以2 000 m/s速度在空气中运动时，气动阻力在105N量级，弹丸在膛内加速到1 000 m/s以后，其绝对数值已经超过了电枢与导轨接触产生的摩擦力(运动摩擦力103～104N量级)[6-7]。电磁轨道发射器装置绝缘板设计需要充分考虑材料绝缘性、耐高温、气动力影响，另外动态发射试验场地设计、试验设施防护措施制定，都要求掌握膛口激波发展规律。

2009年，美国航空航天学会(AIAA)通过气动阻力研究，证实结构网格具有比非结构网格更高数值精度[8]。徐嘉等[9]通过采用多层多块隐式嵌套重叠网格方法，以美国国家航空航天局- 民机共用研究模型(NASA-CRM)翼型为研究对象，进行了阻力数值预报，计算结果与高超声速气动力计算软件CFL3D和OVERFLOW对比具有较高一致性。多块结构重叠网格方法因其相对传统结构网格适用性强[10]，相对非结构网格计算效率高[11]，对弹丸动态发射数值模拟具有较好适用性。迄今为止，鲜有文献采用计算流体动力学(CFD)进行电磁轨道发射器膛内、膛口气动分布数值计算。因此，研究弹丸运动过程波阻变化规律，分析电磁轨道发射器膛口流场发展过程，确定激波对流场参数影响，具有重要意义。

本文采用多块结构重叠网格方法，对计算域分区、对象之间重叠生成计算网格，通过Java程序实时更新弹丸运动速度，弹丸出膛口后利用六自由度运动模型模拟其惯性运动，实现弹丸动态发射过程流场分析。重点研究了弹丸在膛内运动、出膛口过程和空气域运动过程中流场参数分布、阻力系数变化规律以及膛口流场发展规律。

1 计算模型

1.1 物理模型简化

电磁轨道发射器弹丸运动过程中，依靠电枢受到洛伦兹力推动弹丸做变加速运动。电磁轨道发射器弹丸运动控制方程[12]为

(1)

式中：FD为弹丸运动时与炮膛摩擦产生总阻力，取FD=10 kN[11]；Fd为空气阻力；mp为弹体质量；ma为电枢质量；vp为弹丸运动速度。

弹丸在电磁轨道发射器膛内做变加速运动，出膛口后靠惯性向前运动。本文利用计算流体动力学Starccm+软件和对软件的二次开发，采用重叠网格技术实现弹丸动态发射：通过Java程序将图1所示速度曲线嵌入软件，并以此作为输入，驱动弹丸重叠域在膛内运动，通过六自由度运动模型实现弹丸出膛口后惯性运动。

设计4个算例研究电磁轨道发射器弹丸动态发射过程流场分布、膛口流场发展过程和激波阻力变化规律。图1为弹丸膛内运动过程速度变化曲线。

建立电磁轨道发射器二维简化动态发射运动模型，如图2所示。模型参数：弹丸尺寸420 mm×200 mm，动态发射域：导轨尺寸130 mm×1 200 mm，空气域尺寸为12 000 mm×3 500 mm. 计算域共设计了19个压力监测点，位置分布如图3所示，其中点1坐标为(0.5 m，0.2 m)。

1.2 控制方程和湍流模型

重叠网格中，积分形式的二维可压缩雷诺平均N-S方程[13-14]为

(2)

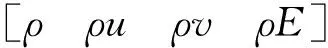
选用Realizablek-ε湍流模型对计算模型进行封闭，在文献[15]中该模型改进了经验常数 ，并得到了该常数与应变率的数值关系式，在工程中得到大量应用，其k和ε的输运方程[15-16]为

(3)

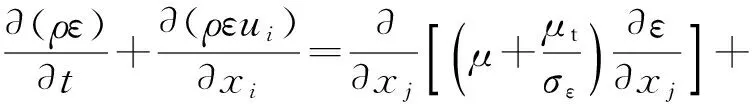
(4)

式中：σk=1.0；σε=1.2；C2=1.9；

(5)

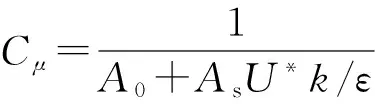
(6)

其他参数定义可见文献[15]。

1.3 多块结构重叠网格和网格划分方案

电磁轨道发射器装置膛口尺寸0.1 m量级，弹丸出膛口后影响区域为膛口尺寸10倍以上，这就导致单区域网格划分局限性，出膛口后空气域网格尺寸难以控制。多块网格针对此类问题具有很好的适应性，图3(a)为多块网格划分机理，将计算域切分，分别进行网格划分，计算域之间必须满足：计算域封闭、无交叉，各区域之间设定数据交互界面，依靠接口(Interface)进行数据传递。

本文算例弹体尺寸远小于计算域尺寸，尤其是弹丸重叠域，膛内单边缝隙只有0.015 m，而出膛口后计算域尺寸在1 m量级，造成网格划分尺寸选择矛盾。重叠网格因其对各个重叠域网格无特殊要求，并且可以相对自由地控制各个域网格划分，故可以较好地解决此类问题。

图4为网格划分方案。使用网格划分ICEM软件划分各个子区域结构网格，通过接口界面实现不同子区域网格之间的数据传递，以弹体为对象创建重叠域网格，通过重叠网格接口创建最终多块结构重叠网格。图3(b)为重叠网格边界和重叠网格内部数据插值原理图。选用最小二乘插值方法进行数值插值，确保重叠网格子区域之间数据传递隐式耦合。(7)式为图3(b)中网格C的流动参数计算公式：

φ=∑αiφi,

(7)

式中：αi为插值权重系数；φi为图3(b)中网格C周围6个网格对应流动参数值，3个为重叠域流动参数，3个为背景域流动参数。

1.4 网格划分结果和数值求解方法

为了验证网格密度对计算结果的影响，共设计4种网格密度方案，如表1所示。图5为4种网格划分方案下的工况1阻力系数计算结果。由此可知：弹丸在膛内运动时，随着网格密度增加，阻力系数Cd计算结果有一定增大趋势；弹丸出膛口过程中，阻力系数变化趋势一致，只有网格划分方案1与其他3种方案差异较大；弹丸在空气域运动时，网格划分方案1与其他3种方案开始出现较大偏差。因此，选取方案3(即背景域网格数量为44万，重叠域网格数量为2.8万)进行后续工况数值计算。图6为方案3对应网格划分结果。

表1 网格划分方案

根据Realizablek-ε湍流模型对y+要求，通过多次试算和网格调整，最终确定y+分布在35～60，网格质量保证在0.85以上，正交性均大于36°.

本文算例中，弹体采用固壁(Wall)边界条件，重叠域边界为重叠网格交互面，导轨为固体边界条件，空气域边界垂直于弹丸运动方向为自由流(freestream)，沿弹丸运动方向为固壁边界条件，初始流场压力为p0=101 325 Pa，温度为300 K，不考虑重力作用影响。采用基于密度求解器方法和2阶隐式耦合流体处理方法，时间步长选用10-6s，以保证计算结果流场细节捕捉能力。

2 模型验证

2.1 计算对象和问题分析

高超声速流动CFD数值模拟准确性问题一直以来备受学者关注。李素循[16]做了大量超音速、高超音速风洞试验，为开展高超音速CFD数值模拟提供了认证依据。为研究建立计算模型准确性和可靠性，基于该方法进行了双椭球表面压力分布数值计算，结果与李素循[16]炮风洞试验结果进行了对比。

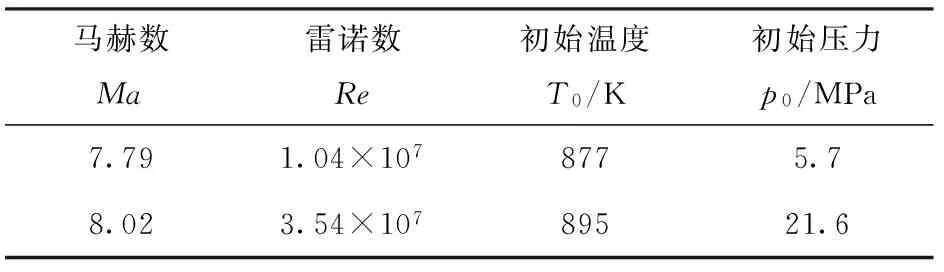
利用Starccm+软件分别生成以双椭球为对象的重叠域网格和以计算流域为对象的背景域网格，计算过程中，通过直接旋转重叠域网格实现变攻角工况下双椭球风洞试验数值模拟，椭球表面网格和重叠域附近网格如图7所示。流动边界为自由流，计算工况选取文献 [16]中工况，如表2所示。

2.2 计算对象和问题分析

数据处理中，根据测得绝对压力进行计算。文献[16]中定义：将双椭球0°攻角下首部第1测压点的值，记为来流皮托压力pP；通过(9)式即可确定马赫数Ma，确定计算条件。

马赫数Ma雷诺数Re初始温度T0/K初始压力p0/MPa7.791.04×1078775.78.023.54×10789521.6

Cp=(p-p∞)/q,

(8)

(9)

式中：γ为比热比；pP为皮托压力(MPa)；p∞为来流静压(MPa)；q为来流动压(MPa)；Cp为压力系数。

通过数值模拟，分别得到了Ma为7.79、8.02时，攻角0°、-5°、10°、20°条件下的双椭球子午线上表面压力系数分布，如图8、图9所示，实线表示数值模拟监测结果，离散点表示试验测量值。

两种马赫数条件下，双椭球上表面、下表面压力系数计算(见图8、图9)结果表明：压力系数随x值的增大先减小、后增大，呈现波动变化趋势，在波动区域附近，4种攻角条件下计算结果存在一定误差，但是仍然可以接受，其主要原因是由于上椭球附近存在激波，导致发生流动分离、压力上升，降低了CFD对流动捕捉能力；在模型后部，无激波干扰区域，压力系数变化平缓，数值仿真结果与试验结果展现了较好的一致性。

不同攻角下，压力系数变化表明：随着攻角增大，双椭球上表面压力系数减小趋势趋于陡峭，其主要原因是由于攻角增大，纵向分离流场尺寸增大，即由于激波影响的位置会发生后移；双椭球下表面压力系数分布，下降速率先快后慢，攻角越大，压力系数越大，马赫数和雷诺数对压力系数分布影响不大。

通过该算例验证了定常数学模型对高超声速流场的计算准确性以及重叠网格在零攻角和变攻角条件下数据交互的准确性和适用性。

3 计算结果与分析

弹丸在膛内运动时形成弹前激波，对于加速运动过程，随着速度增大，后面压缩波会逐渐赶上弹体头部压缩波，形成如图10所示的激波。对于弹前激波，其波阵面压力峰值、激波距弹体头部距离主要取决于弹丸速度变化规律。图10为弹丸动态发射过程中，激波出膛口时的压力云图。此时，弹体头部开始泄压，此刻为激波阵面峰值压力点，随后激波阵面压力将迅速降低，并且波阵面处不再是整个流场压力峰值区，压力峰值开始向弹体头部及头部两侧转移。

图11(a)为弹丸头部出膛口时的流场压力分布云图。与传统火炮不同的是，电磁轨道发射器在动态发射试验中，发射器尾部直接与空气接触，所以弹丸运动过程中，弹底不仅没有高压气体存在，而且出现了负压；弹体头部侧面也有负压存在。图11(b)、图11(c)分别为此刻马赫数等值线分布和速度矢量分布。由此可知：弹体头部两侧马赫数最大，速度矢量结果可以确定是由弹体与导轨内高速气流快速流出造成的；弹体底部和头部马赫数较大，一方面是由于弹体和导轨缝隙内气流快速流出，另一方面弹体后部气流影响。负压存在主要是由于高速气流运动产生快速“抽吸”作用造成的。在此刻，弹体头部中点附近已经转换成为压力峰值区。

图12为弹丸尾部出膛口时的流场压力分布云图和速度矢量图。计算结果表明，弹体尾部出膛口过程中，已经形成了球形激波，头部出现了冠状激波。对于电磁轨道发射器装置，弹体和导轨之间存在8～10 mm间隙。由图11(c)可知：间隙的存在导致缝隙内气流高速流出，一部分在膛口形成了较大速度梯度；另一部分流向弹体头部，导致激波阵面出现了不连续；中间部分向外凸起，形成明显冠状激波。图12弹丸尾部出膛口时，受缝隙内气流影响较小，冠状激波已经开始慢慢变小。图13中弹丸头部已经形成了连续脱体激波。

图13(a)为弹丸尾部出膛口时，流场压力分布云图，图13(b)为激波阵面压力分布。由此可知，空气域弹丸稳定飞行后，形成了弓形脱体激波，压力峰值区重新出现在激波阵面，并且激波阵面存在很大压力梯度。

上述计算结果表明，电磁轨道发射器弹丸在动态发射过程中可以依据弹前激波出膛口、弹体头部出膛口、弹体尾部出膛口将电磁轨道发射器动态发射过程分为4个阶段：1)弹前激波开始出膛口前运动阶段；2)弹体头部开始出膛口前运动阶段；3)弹体尾部开始出膛口前运动阶段；4)弹体在空气域运动阶段。

图14～图16分别给出了工况1、工况2、工况3动态发射过程中弹体头部中点、弹体尾部中点、弹体侧面点绝对压力变化数值仿真结果。基于上述4个阶段，结合CFD仿真结果进行分析。

第1阶段：弹前激波开始出膛口前运动阶段。图14表明，弹体头部压力出现了陡降- 增大过程，由于此3种数值模拟工况不存在加速过程，速度直接达到峰值，随着弹丸运动，脱体激波发展开始趋于稳定，所以压力开始减小，随着激波的发展充分压力开始增大。由图15可以确定，在弹前激波进入空气域前，随着弹丸运动弹底压力逐渐增大，初始时刻存在小的跃升，随着速度增加，弹底压力有下降趋势，但3种工况差别不大。由图16可以确定，在弹前激波进入空气域前，弹体侧面点(弹体上侧面后三分之一位置)处压力起始增长缓慢，随后增速加快。随着弹丸运动速度的增加，弹体侧面点压力有增大趋势。

第2阶段：弹体头部开始出膛口前运动阶段。激波出膛口后迅速膨胀，开始形成初始激波即初始流场，也就是图10～图11流场发展的中间阶段。由于数值实验工况导轨长度0.12 m，在大约0.24 ms(工况1)时弹体头部脱体激波已经开始离开导轨，如图10所示。图14表明，弹丸在头部开始出膛口前，弹体头部压力逐渐降低，因为膛口激波突然释放，弹体头部随着压力泄放，压力逐渐降低，随着高压激波不断向前形成了球形激波阵面。图15和图16的计算结果表明，在此阶段，弹体尾部和弹体侧面点不受激波出膛口影响，继续保持增大，增大速率变化不大，与第1阶段变化趋势保持一致。在弹丸头部开始出膛口时刻，初始流场形成结束。

第3阶段：弹体尾部开始出膛口前运动阶段。图14表明：此阶段弹体头部压力先减小、后增大，减小和增大过程时间各占50%左右；不同速度工况下，压力下降阶段变化趋势基本一致；上升阶段，不同速度工况上升趋势出现了波动；尾部出膛口时弹体头部压力基本上与弹前激波出膛口时保持一致。此阶段由于泄压作用，会导致弹体头部压力进一步降低。但是随着弹丸在空气域运动，球形激波进一步发展和冠状激波逐渐形成，会进一步导致弹体头部压力升高。此阶段，压力峰值区出现在弹体头部，随后逐渐向激波阵面转移。图15表明：弹底压力出现了相反的变化趋势，主要是由于在弹丸尾部出膛口前，弹体与导轨间隙内高速气流快速流向弹底(如图12弹底速度矢量图)，导致弹底压力出现急剧下降趋势。图16表明：弹体侧面点在出膛口前，压力一直保持上升趋势，接近膛口时上升速率减小，出膛口后压力迅速降低，主要是由于弹体侧面点在进入空气域后开始泄压造成；在侧面点出膛口前一小段，不同速度工况弹体侧面点压力出现了较大差异。电磁轨道发射器装置包含引弧，引弧装置将剩余电能消耗后会产生等离子体和高强弧光，弹丸出膛口后，可以明显观察到装置尾部喷射出弧光， 图14和图15的弹体头部压力计算结果表明，由于弹体头部、尾部存在兆帕级压差，会导致该试验现象发生。

第4阶段：弹体在空气域运动阶段。图14表明：弹体头部压力开始降低，然后逐渐增大稳定。因为此时动球心的球形激波和冠状激波开始向脱体激波过渡，完成过渡后弹体头部压力会逐渐趋于稳定；随着弹丸运动速度增大，弹体头部压力增大。图15表明，弹底压力在出膛口后出现了跃升现象，随后增大趋于稳定，由图17可以确定，弹底压力跃升主要是由于弹体尾部高速气流影响。图16表明，此阶段弹体侧面点压力值基本趋于稳定，同样由于高速气流影响压力出现了小幅跃升，不同速度工况压力差别不大。

图18为4种速度工况下的弹丸动态发射过程阻力系数变化规律。图14和图18对比表明，阻力系数与弹体头部中点压力变化规律具有较好一致性，因为激波阻力主要包括压差阻力和摩擦阻力，且以压差阻力为主，而弹底压力始终保持一个比较低的数值，因此阻力系数结果对弹体头部压力依赖性较强。阻力系数主要变化趋势与弹体头部压力变化相似，原因也基本相同，此处不再分析。工况4计算结果表明，弹丸膛内变加速运动过程中，阻力系数逐渐增大，起始时刻由于弹丸绝对速度较小，阻力系数增速较慢，随着弹丸速度增大，阻力系数快速增大，速度达到最大时阻力系数也达到最大。工况4弹丸以1 954 m/s速度出膛口，与工况1出膛口后阻力系数变化规律相似。

为了分析远场激波对流场的影响，图19～图22给出了弹丸动态发射过程中，工况1和工况2条件下16个监测点(监测点布置见图2)压力变化规律，考虑到数据量，这里只列举前两个工况。

弹丸在弹体尾部出膛口后，靠惯性向前高速飞行，图19和图20给出了运动坐标系上y分别为0.2 m和0.6 m处8个监测点压力变化规律。计算结果表明：各个监测点压力初始时刻比较小，随后陡增，到达峰值压力后以指数规律降低，距弹丸轴向距离越远，压力降低速率越小；弹丸速度越高，峰值压力越大，由表3可知，工况1和工况2相同监测点最大相差16.1%. 弹丸头部脱体激波经过监测点时，波阵面前侧先接触监测点，波阵面前压力梯度非常大(见图13(b))，短时间内压力达到峰值，监测点压力分布规律实际上也是激波阵面前压力、后压力分布规律。

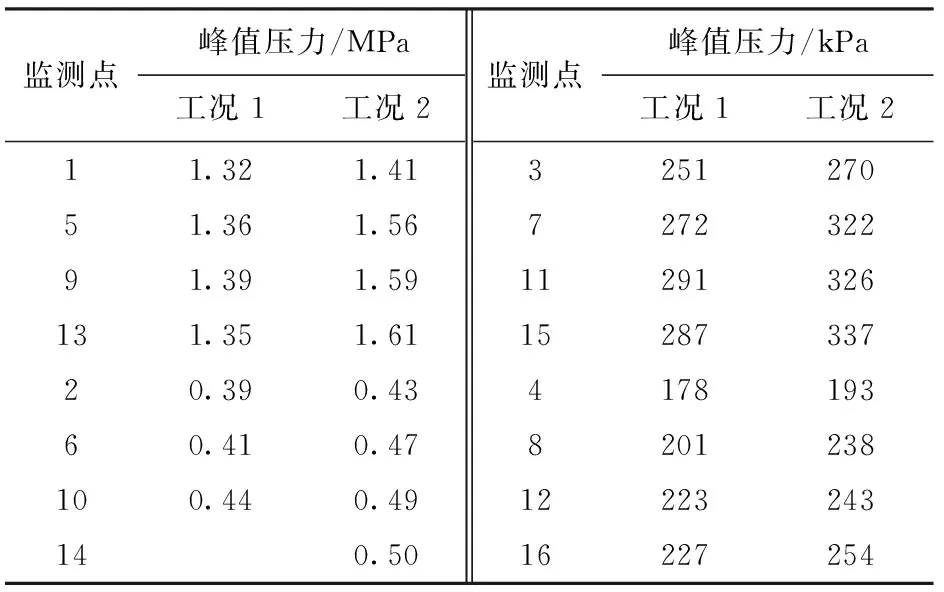
表3 监测点首次峰值压力

表3为16个监测点在两种计算工况下峰值压力，结果表明：相同工况下，相同垂向维度的峰值压力变化不大；随着距弹轴垂向距离增大，监测点峰值压力快速衰减。

本算例计算域中，弹丸距离壁面距离为1.5 m. 图21的计算结果表明：弹丸以2 000 m/s速度出膛口时，距壁面0.5 m处监测点(2.5 m，1.0 m)在0.25 ms左右第1次达到压力峰值；随着激波到达壁面，反射后在0.47 ms左右第2次达到峰值。不同监测点弹丸速度衰减两次峰值压力时间差会有区别，由于激波快速移动，工况1监测点两次峰值之间时间差都在0.22 ms左右。工况2相同监测点峰值压力明显高于工况1，因为工况2出膛口速度大于工况1.

图22为距离弹体轴向距离1.4 m处4个监测点压力变化规律。工况1中，弹丸以2 000 m/s速度出膛口，弹体头部激波强度快速减弱，随着流场稳定，强度较弱激波到达壁面，在壁面发生正则反射，计算结果可以明显看到激波反射对监测点压力的影响，并且反射压力明显高于监测点首次峰值压力，这与实际不符，因为激波撞击壁面后会有能量损失，损失能量后激波反射压力绝对值不可能超过反射前，通过对弹丸监测点处压力场分布分析(见图22中压力云图)，监测点处测得压力是反射激波和激波本身重叠，导致反射后峰值压力高于反射前峰值压力。

通过图21和图22的计算结果对比可以确定：监测点距弹轴越远，反射周期越小。

4 结论

本文通过采用多块结构重叠网格方法，同时辅助以弹丸运动规律Java程序和六自由度运动模型，进行了4种工况下的电磁轨道发射器动态发射过程流场计算，确定了弹丸动态发射过程流场参数变化和膛口流场发展规律。得到主要结论如下：

1)验证了超高声速条件下，重叠网格数据交互可靠性、建立数值模型适用性、网格无关性。电磁轨道发射器动态发射过程是含复杂激波系流场，主要包括4个运动阶段：在膛内主要是弹前激波和反射激波叠加；激波出膛口后由于泄压，开始形成球形激波和冠状激波；弹体头部出膛口后，由于缝隙高速气流影响，膛口开始形成高速气流区，直至弹丸尾部离开膛口，逐渐形成球形激波、冠状激波共同作用；弹丸在空气域运动时，逐渐演化为脱体激波。

2)弹前激波出膛口到弹体尾部出膛口过程中，弹体头部中点压力分布呈现“对称性”，弹前激波出膛口时达到峰值，弹丸尾部出膛口时再次达到峰值。阻力系数分布和弹体头部压力分布具有相关性，弹前激波出膛口后呈现先减小、后增大的“弱对称性”，弹体尾部出膛口时达到峰值。

3)弹丸在空气域运动时，因为反射激波与激波本身叠加作用，近壁面压力监测点反射后的峰值会超过初始监测点压力峰值，距弹轴距离越远，反射周期越小，监测点峰值压力衰减越慢。

)

[1] Watt T J，Bryant M D. Modeling assumptions for railguns[J]. IEEE Transactions on Magnetics， 2007，43(1):380-383.

[2] 林庆华, 栗保明. 电磁轨道炮瞬态磁场测量与数值模拟[J]. 兵工学报，2016，37(10)：1788-1794.

LIN Qing-hua, LI Bao-ming. Measurement and numerical simulation of transient electromagnetic field in railgun[J]. Acta Armamentarii, 2016, 37(10):1788-1794. (in Chinese)

[3] Rodger D，Leonard P J．Modeling electromagnetic performance of moving rail gun launchers using finite elements[J]．IEEE Transactions on Magnetics，1993，29(1)：496-498．

[4] 谭赛, 鲁军勇, 张晓, 等. 电磁轨道发射器动态发射过程的数值模拟[J]. 国防科技大学学报, 2016, 38(6):43-48.

TAN Sai, LU Jun-yong, ZHANG Xiao, et al. Numerical simulation of dynamic launching in electromagnetic rail launcher[J]. Journal of National University of Defense Technology, 2016, 38(6):43-48.(in Chinese)

[5] Gennady G A，Stankevich S V．Comparison between 2-D and 3-D electromagnetic modeling of railgun[J]．IEEE Transactions on Magnetics，2009，45(1)：453-457．

[6] 时光，陈忠华，郭凤仪. 强电流滑动电接触下最佳法向载荷[J].电工技术学报，2014，29(1)：23-30.

SHI Guang, CHEN Zhong-hua, GUO Feng-yi. Optimal normal load of sliding electrical contacts under high current[J]. Transactions of China Electroechnical Society, 2014, 29(1):23-30. (in Chinese)

[7] 田振国，孟晓永，安雪云，等. 电磁轨道发射状态下的复合导轨动态响应研究[J].兵工学报，2017，38(4)：651-657.

TIAN Zhen-guo, MENG Xiao-yong, AN Xue-yun, et al. Dynamic response of composite rail during launch process of electromagnetic railgun [J]. Acta Armamentarii, 2017，38(4)：651-657.(in Chinese)

[8] Vassberg J C, Brodersen O P，Wahls R A， et al. Summary of the fourth AIAA CFD drag prediction workshop[C]∥The 1st AIAA CFD High-Lift Prediction Workshop. Chicago，IL, US： AIAA, 2010.

[9] 徐嘉，刘秋洪，蔡晋生，等. 基于隐式嵌套重叠网格技术的阻力预测[J].航空学报，2013,34(2)：208-217.

XU Jia, LIU Qiu-hong, CAI Jin-sheng, et al. Drag prediction based on overset grids with implicit hole cutting technique[J]. Acta Aeronautica et Astronautica Sinics, 2013, 34(2): 208-217. (in Chinese)

[10] Blanc F．Patch assembly：an automated overlapping grid assembly strategy [J]. Journal of Aircraft，2010，47(1)：110-119．

[11] Wang J Z, Parthasarathy V. A fully automated chimera methodology for multiple moving body problems[J]. International Journal for Numerical Methods in Fluids，2000，33(7)：919-938．

[12] 王莹，肖峰．电炮原理 [M]．北京：国防工业出版社，1995．

WANG Ying，XIAO Feng. Principle of electric gun[M]. Beijing: National Defense Industry Press, 1995. (in Chinese)

[13] Blazek J. Computation fluid dynamics：principles and applications[M]. UK:Elsevier Science Ltd，2001.

[14] Noack R W. Dirtlib：a library to add an overset capability to your flow solver[C]∥Proceedings of the 17th AIAA Computational Fluid Dynamics Conference. Toronto，Ontario, Canada：AIAA, 2005: 2005-5116.

[15] Shih T H, Liou W W, Shabbir A, et al. A newk-εeddy viscosity model for high Reynolds number turbulent flows[J]. Computers & Fluids, 1995, 24(3):227-238.

[16] 李素循. 典型外形高超声速流动特性[M]. 北京：国防工业出版社，2007.

LI Su-xun. Hypersonic flow characteristics of typical shape[M]. Beijing: National Defense Industry Press, 2007. (in Chinese)