对称刻槽预控破片战斗部壳体爆炸过程质量损失率研究

张高峰， 李向东， 周兰伟， 马丽英

(南京理工大学 智能弹药技术国防重点学科实验室, 江苏 南京 210094)

0 引言

预控破片技术是指通过特殊措施控制战斗部壳体破碎，从而控制壳体破碎形成破片的形状和尺寸，进而提高杀伤战斗部的威力[1]。常用的预控破片技术有战斗部壳体表面刻槽、装药表面刻槽、壳体内嵌金属罩等。壳体表面对称刻槽，因加工工艺简单、预控效果好成为常用的预控破片技术。壳体在破碎过程中因为预控刻槽的作用，按一定的断裂迹线断裂，该过程中壳体被撕裂掉一些金属碎渣，造成质量损失的壳体质量与预刻槽后壳体总质量的比值称作壳体爆炸质量损失率。战斗部装药爆轰波掠过壳体内侧对壳体会产生粉碎作用，亦会带来壳体质量损失，但此过程复杂且由此造成的质量损失很少，因此本文不考虑该质量损失。爆炸过程壳体质量损失率研究有助于战斗部设计者准确地计算预控破片的质量，从而控制战斗部的威力。研究壳体爆炸质量损失率，首先需研究预刻槽壳体的断裂方式。国内外学者对壳体刻槽式预控破片战斗部的壳体断裂问题进行了相关研究[2-3]。吴成等[4-5]以内刻V形槽战斗部圆柱壳体为研究对象推导出了内刻槽圆柱壳体的临界断裂应变判据，并研究了不同热处理条件下内刻V形槽20号钢圆柱壳体的断裂机理，发现壳体裂纹开始于刻槽根部, 从壳体内表面延伸至外表面, 引起壳体破裂。Pearson[6]认为，内刻槽式壳体断裂迹线走向与内表面切线的方向约成45°. Richard[7]认为对称刻槽的情况，断裂迹线剖面将趋于产生相等数目主迹线和副迹线。刘桂峰等[8]研究了刻槽参数对破片形成的影响，同时对外刻槽式预控破片战斗部壳体断裂模型进行了简化，亦认为断裂是从刻槽根部开始，裂纹以剪切断裂方式扩展，呈45°剪切角。对于由沿周向刻槽而产生的断裂迹线的走向问题及壳体爆炸质量损失率方面的研究未见相关文献报道。

为研究内对称刻槽式预控破片战斗部壳体爆炸过程质量损失率，本文分析了战斗部壳体分别沿轴向和周向内对称刻槽所引起的断裂迹线走向问题，对典型内对称刻槽预控破片战斗部爆炸过程壳体质量损失率进行了理论计算，同时开展了相关试验验证了壳体断裂迹线的走向，并通过试验数据验证理论分析结果的准确性。

1 对称刻槽预控破片战斗部壳体断裂形式

1.1 刻槽阵列及形态

战斗部内炸药被引爆后，产生高温高压的爆轰气体。高压气体作用下，壳体在预刻槽根部产生应力集中，并在此处沿特定走向的迹线断裂。壳体刻槽参数及分布决定破片的形状、尺寸及数目，因此可以通过刻槽参数和刻槽阵列分布来控制壳体破碎产生破片的形状、尺寸及数目[9-10]。壳体内表面刻槽列阵分布形式可分为菱形列阵模式和矩形列阵模式，两种列阵模式均可控制破片的形成，两种刻槽列阵模式示意图如图1(a)和图1(b)所示，图1中ri为战斗部壳体内半径，h为战斗部壳体长度。因菱形刻槽列阵模式加工工艺复杂，壳体两端会产生半破片，减小了有效破片数目，因此在实际战斗部设计中常采用矩形刻槽列阵模式。本文主要研究图1(b)中所示矩形刻槽列阵刻槽方式，此种战斗部壳体在周向与轴向均刻有对称V形槽，其中：对于沿轴向的V形槽，每一V形槽均与壳体周向垂直的平面(见图2(a)中x平面)对称，且该平面通过刻槽根部；对于沿周向的V形槽，每一V形槽均与壳体轴向垂直的平面(见图2(b)中y平面)对称，且该平面通过刻槽根部。

1.2 壳体沿轴向刻槽引起的壳体断裂形式

在爆炸气体作用下，战斗部壳体膨胀过程中，壳体沿轴向的预刻槽促使壳体在横截面上产生断裂迹线。当断裂迹线完全贯通壳体时，壳体将破碎成分散的破片。此过程中壳体受到拉应力与切应力的联合作用，壳体的断裂问题可用断裂力学中的最大环向拉应力理论求解，根据该理论，战斗部壳体裂纹沿周向应力σθ最大方向(最大主应力)起裂扩展[11]，战斗部壳体刻槽尖端附近的应力分量如图3所示，σr为径向应力。

该应力场[12]在极坐标中可表示为

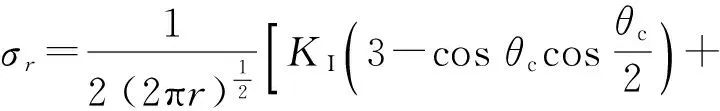
(1)

(2)

式中：KⅠ、KⅡ分别为Ⅰ型、Ⅱ型断裂模型所对应的应力强度因子；θc为断裂迹线走向与过刻槽底端的壳体横截面上半径之间的夹角。

为求σθ的最大值，将(2)式对θc求导，可得

(3)

(4)

1.3 壳体沿周向刻槽引起的壳体断裂形式

壳体在膨胀过程中，沿周向刻槽根部亦会引起应力集中，使壳体在纵向剖面上也产生断裂迹线。战斗部壳体沿周向的刻槽处上下部分因爆轰气体的膨胀速度不同，产生压力差，此压力差将促使壳体在刻槽根部产生剪切作用，相对于此剪切力，刻槽根部受到的拉应力可忽略，壳体沿周向刻槽的槽根处受力状态如图5所示。

根据断裂力学中的应变能密度因子理论，裂纹沿着有应变能密度因子极小的方向扩展，应变能密度因子[12]为

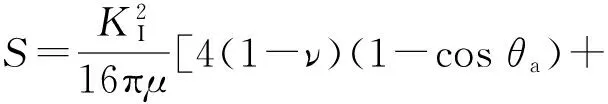
(5)

式中：μ为剪切弹性模量；ν为泊松比；θa为断裂迹线与过槽底半径的夹角。

为求得S在何处取得最小值，对θa微分，得

(6)

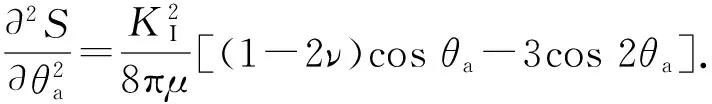
(7)

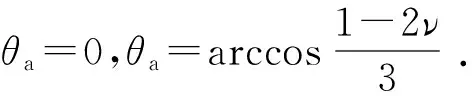
(8)

当θa=0时，得

(9)

因而S在裂纹的延长线方向有极大值。

当θa=arccos[(1-2ν)/3] 时，得

(10)

因而S在此方向有极小值。

由此可知θa=arccos[(1-2ν)/3]为开裂方向。由于裂纹扩展方向近似于与主拉伸应力方向垂直(见图5)，θa角取负值，即

θa=-|arccos[(1-2ν)/3]|.

(11)

综上所述，壳体轴向排布的刻槽阵列促使每一刻槽根部均产生一条断裂迹线，并且所有从根部产生的断裂迹线走向都平行，断裂迹线走向如图6所示(图6中虚线)，因此在壳体爆炸过程中，沿周向方向的刻槽不会给壳体带来质量损失。

2 对称刻槽预控破片战斗部壳体爆炸质量损失率计算

2.1 壳体爆炸质量损失率计算模型

刻槽深度不同，断裂迹线交汇形成大小不同的破片。壳体的周向横截面如图7所示，图7(a)、图7(b)和图7(c)分别对应3种特殊刻槽深度所产生的剪迹线。在某一刻槽深度下相邻刻槽引起的断裂迹线相遇于壳体外壁，如图7(a)所示，此时的临界刻槽深度ec为

(12)

式中：ro为战斗部壳体外半径；Na为沿轴向方向的刻槽份数。

当刻槽深度e小于ec时，相邻刻槽引起的断裂迹线相遇于内外壁之间，如图7(b)所示；当刻槽深度e大于ec时，相邻刻槽引起的断裂迹线相遇于壳体外部，如图7(c)所示。

如果壳体满足图7(a)和图7(b)中对应的刻槽深度，该壳体在断裂过程中会产生双层破片，两层破片质量不一致，在实际战斗部设计中常采用图7(c)所示的刻槽深度。本文研究图7(c)所示刻槽深度的壳体爆炸质量损失率计算模型。

如图7(c)所示，沿槽底左右两条断裂迹线与壳体外表面之间的部分为破片爆炸过程的质量损失，此部分的周向横截面积为

(13)

式中：

(14)

α为刻槽半顶角。

爆炸过程壳体的质量损失为

mb=S′hNaρ，

(15)

式中：ρ为壳体密度。

壳体爆炸质量损失率为

(16)

式中：ma为壳体刻槽后的质量。

2.2 壳体爆炸质量损失率算例

参考典型战斗部壳体尺寸设计了两种模拟战斗部：第1种模拟战斗部在壳体内侧分别沿周向和轴向均刻有相同深度且相互平行的对称槽；第2种模拟战斗部采用环形多层破片，单环内采用预刻对称槽，此形式可消除轴向断裂所带来的壳体质量损失。刻槽深度均为2.5 mm，壳体外径为78 mm，壳体厚度为5.5 mm，壳体长度为158.4 mm，周向刻槽份数为24，轴向刻槽份数为18. 根据上述计算模型，计算结果见表1.

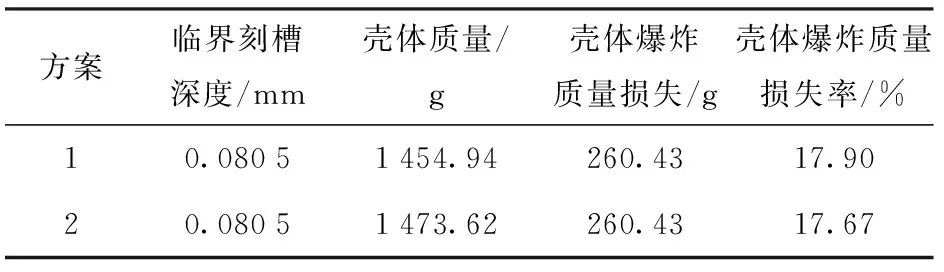
表1 壳体爆炸质量损失率计算结果

3 对称刻槽预控破片战斗部水井静爆试验

3.1 水井静爆试验方案

为验证上述断裂迹线走向的正确性，检验所建壳体爆炸质量损失率计算模型的准确性，按照上述方案加工两种模拟战斗部进行水井静爆破片回收试验，试验原理图如图8所示，试验设置图如图9所示。

每种战斗部加工两发，序号分别为1号～4号(1号和2号战斗部对应方案1，3号和4号战斗部对应方案2)，模拟战斗部均采用端部起爆，模拟战斗部壳体照片如图10所示。

3.2 试验数据处理

试验过程中4号战斗部起爆异常，仅回收到前3发模拟战斗部的破片数据，对回收到的破片进行分拣和干燥处理。对1号战斗部和2号战斗部的破片进行观察发现：破片的断裂面较粗糙，破片周向有两个对称的撕裂面，破片轴向上下两断裂面相互平行。对3号战斗部回收到的破片进行观察发现，破片的断裂面较平整，外侧周向有两个对称的撕裂面。由此可知，沿轴向方向的刻槽促使壳体爆炸过程中，在刻槽根部延伸出两条对称的断裂迹线；沿周向方向的刻槽，会促使壳体爆炸过程中，在刻槽根部延伸出一条断裂迹线。破片照片如图11所示。

对破片进一步称重处理，数据处理结果如表2、表3所示，方案1与方案2的壳体爆炸质量损失相差仅为1.71 g，这说明了壳体在爆炸过程中沿周向刻槽不会带来壳体质量损失。

方案1中壳体爆炸质量损失率试验值为17.24%，理论计算值为17.9%，理论计算与试验数据之间的偏差为3.69%；方案2中壳体爆炸质量损失率试验值为16.31%，理论计算值为17.67%，理论计算值与试验数据之间的偏差为7.70%.

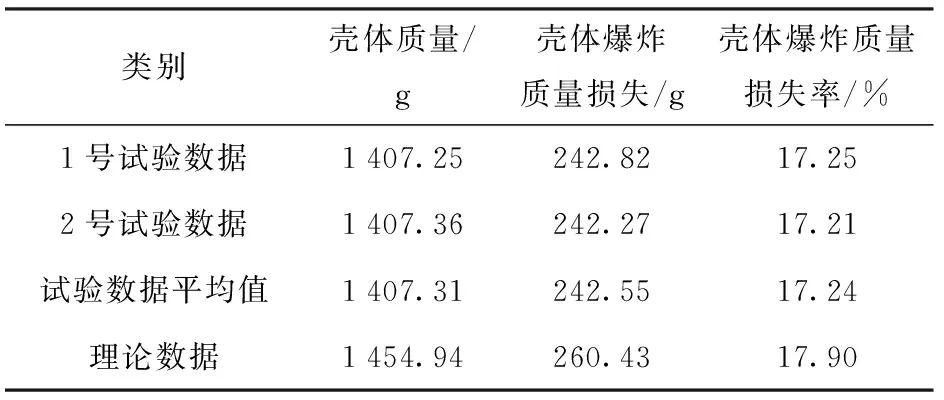
表2 方案1模拟战斗部壳体爆炸质量损失率试验结果

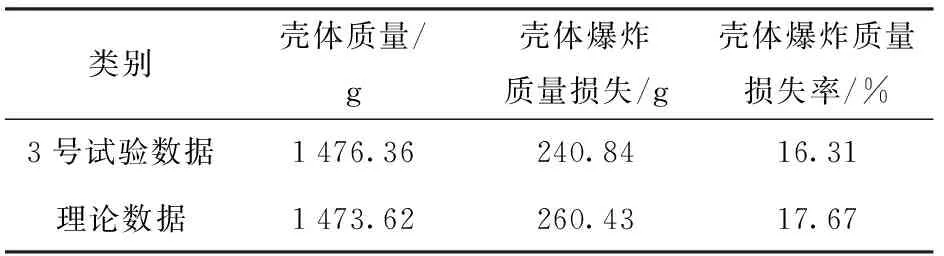
表3 方案2模拟战斗部壳体爆炸质量损失率试验结果

3.3 不同刻槽深度对壳体爆炸质量损失率的影响规律

下面通过理论计算的方法研究不同刻槽深度对爆炸质量损失率的影响。在刻槽深度1～5 mm之间，每隔0.5 mm取一刻槽深度，分别计算方案1、方案2相应的壳体爆炸质量损失率，计算结果如图12所示。

从图12可以看出，随着刻槽深度的增加，两方案中壳体爆炸质量损失率均逐渐减小，方案1爆炸质量损失率略大。但是壳体刻槽深度过大不仅将导致炸药能量在将其最佳能量给与战斗部壳体之前泄露的过快，从而使破片速度低[13]，还会导致战斗部壳体强度降低，因此在战斗部壳体刻槽深度设计过程中壳体刻槽深度不宜过大。

4 结论

1)在战斗部爆炸过程中，壳体上沿周向刻槽不会影响壳体爆炸质量损失，壳体爆炸质量损失与沿轴向刻槽相关。

2)沿周向与轴向均刻槽式战斗部壳体的爆炸质量损失率为17.24%，仅沿轴向刻槽的环形多层破片式战斗部壳体的爆炸质量损失率为16.31%. 理论计算与试验数据偏差小于8%，本文给出的计算方法具有参考价值。

3)刻槽深度越大，壳体爆炸质量损失率越小。

)

[1] 厉相宝, 杨云川, 倪庆杰. 预控破片形成过程的数值模拟与分析[J]. 沈阳理工大学学报, 2009, 28(1):37-40.

LI Xiang-bao, YANG Yun-chuan, NI Qing-jie. Numerical simulation and analysis of the formation of preformed fragments[J]. Journal of Shenyang Ligong University, 2009, 28(1):37-40. (in Chinese)

[2] Taylor G I. Fragmentation of tubular bombs[M].London, UK: Cambridge University Press, 1963: 387-390.

[3] Reid S R. Metal forming and impact mechanics: William Johnson commemorative volume[M]. London, UK:Pergamon Press, 2016:303-323.

[4] 吴成, 倪艳光, 张渝霞. 内刻V形槽半预制破片战斗部壳体的断裂准则[J]. 北京理工大学学报, 2008, 28(7): 569-572.

WU Cheng, NI Yan-guang, ZHANG Yu-xia.Critical fracture criterion on shells of controlled fragmenting warhead with V-notches on their inner surface[J]. Transactions of Beijing Institute of Technology, 2008, 28(7):569-572. (in Chinese)

[5] 吴成, 倪艳光, 张渝霞, 等. 不同热处理条件下半预制破片战斗部壳体的金相观察分析[J].北京理工大学学报, 2008, 28(5): 381-384.

WU Cheng, NI Yan-guang, ZHANG Yu-xia,et al. Metallograpic analysis of semi-preformed fragment warhead steel by different heat treatment[J]. Transactions of Beijing Institute of Technology, 2008, 28(5):381-384.(in Chinese)

[6] Pearson J. Means for controlled fragmentation: US, US4068590[P]. 1978-1-17.

[7] Richard M L. Conventional warhead systems physics and engineering design[M]. Reston, VA, US:AIAA,1998:49-73.

[8] 刘桂峰, 张庆, 沈晓军, 等. 刻槽参数对破片形成的影响[J]. 弹道学报, 2014, 26(2):63-66.

LIU Gui-feng, ZHANG Qing, SHEN Xiao-jun, et al.Effect of groove parameters on formation of fragments[J]. Journal of Ballistics, 2014, 26(2): 63-66.(in Chinese)

[9] Pearson J. The shear-control method of warhead fragmentation[C]∥Proceedings of the 4th International Symposium on Ballistics. Monterey, CA, US: International Ballistics Society ,1978: 17-19.

[10] Pike A W, Zuo Q H. Geometric design consideration for controlled fragmentation of metallic shells[J]. Finite Elements in Analysis and Design,2014, 91: 59-67.

[11] Erdogan F, Sih G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Basic Engineering, 1963, 85(4): 519-527.

[12] 郦正能, 张纪奎. 工程断裂力学[M]. 北京:北京航空航天大学出版社, 2012: 61-73.

LI Zheng-neng, ZHANG Ji-kui. Engineering fracture mechanics[M]. Beijing: Beihang University Press, 2012:61-73.(in Chinese)

[13] Lloyd R. Conventional warhead systems physics and engineering design[M]. Reston, VA, US:American Institute of Aeronautics and Astronautics Inc, 1998: 49-50.