某大跨度悬挂板MTMD减振控制

2018-03-19梁玉青

安徽建筑大学学报 2018年6期

梁玉青

(湖北工业大学土木建筑与环境学院，湖北武汉 430068)

0 引言

大跨结构由于跨度过大容易导致在行人荷载激励下其人体舒适度不满足设计要求。我国规范对大跨结构的1阶竖向振动频率采取了一定的限制要求。如《高层建筑混凝土技术规程》(JGJ3)和《组合楼板设计与施工规范》(CECS 273)要求楼盖结构的竖向振动频率不宜小于3 Hz；《混凝土结构设计规范》(GB 50010)提出对混凝土楼盖结构竖向自振频率的要求更为细致，住宅和公寓不宜低于5 Hz，办公室和旅馆不宜低于4 Hz，大跨度公共公共建筑不宜小于3 Hz。

对于普通悬挂板，在遭受连续跳跃、奔跑等极端荷载作用时，悬挂板可能会因为共振激烈导致其舒适度不符合设计要求。为避免给行人带来不舒适感，需要对大跨悬挂板采取加固或者减振措施，目前多调谐质量阻尼器(multiple tuned mass damper简称MTMD)减振技术已被广泛用于解决大跨结构振动舒适度问题[1-4]，并具有较好的减振效果。但目前对于MTMD加装位置和相关设计参数缺乏充分研究。本文根据某大跨度悬挂板实际工程结构的模态特性，进行详细的有限元分析，以确定不同参数和加装位置MTMD结构在不同荷载工况下的振型频率和该振型幅值，确保悬挂板共振状态下竖向加速度响依然低于舒适度限值，从而充分发挥MTMD的减振性能，有效避免了给板上行人带来不舒适感。

1 工程概况

本工程为钢-筋混凝土组合结构，需要分析的悬挂板处于整体结构的第二层西侧。悬挂板结构三维示意图如图1所示，该悬挂板长度约为32 m，宽度约为12 m，外围由18根直径为60 mm的Q345钢杆吊挂固定。悬挂板的梁板构件材料分别为Q345钢和C40混凝土。整体结构布局合理清晰，对大跨度悬挂板MTMD减振控制的研究具有较好的应用价值。

图1 整体结构三维结构示意图

2 悬挂板模态分析

准确计算结构的模态特性是舒适度评价的前提。大跨度悬挂结构受力复杂，需要筛选出悬挂板结构的竖向振动情况。通过Midas Gen软件采用Ritz法并取45阶振型对整体结构进行模态分析，模态分析结果显示，结构从第4阶开始出现悬挂板的竖向振型，表1列出了整个结构下悬挂板竖向振动的前6阶振型振动情况，其中悬挂板前6阶竖向振型幅值处节点位置如图1所示，图2给出了悬挂板前3阶竖向振动时整体结构振型图。从表1可以看出，悬挂板第1、2阶固有频率在行人荷载频率(1.5～3.5 Hz)以内，行人活动较为容易激发悬挂板产生剧烈运动，故本文研究悬挂板第1、2阶竖向振型，验算不同人行激励下悬挂板舒适度。

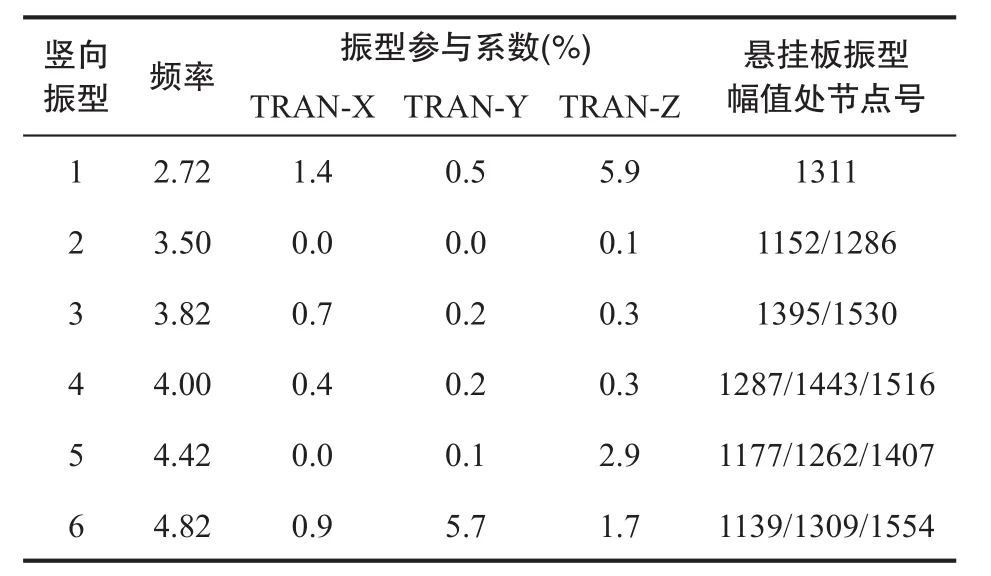
表1 悬挂板的竖向模态情况

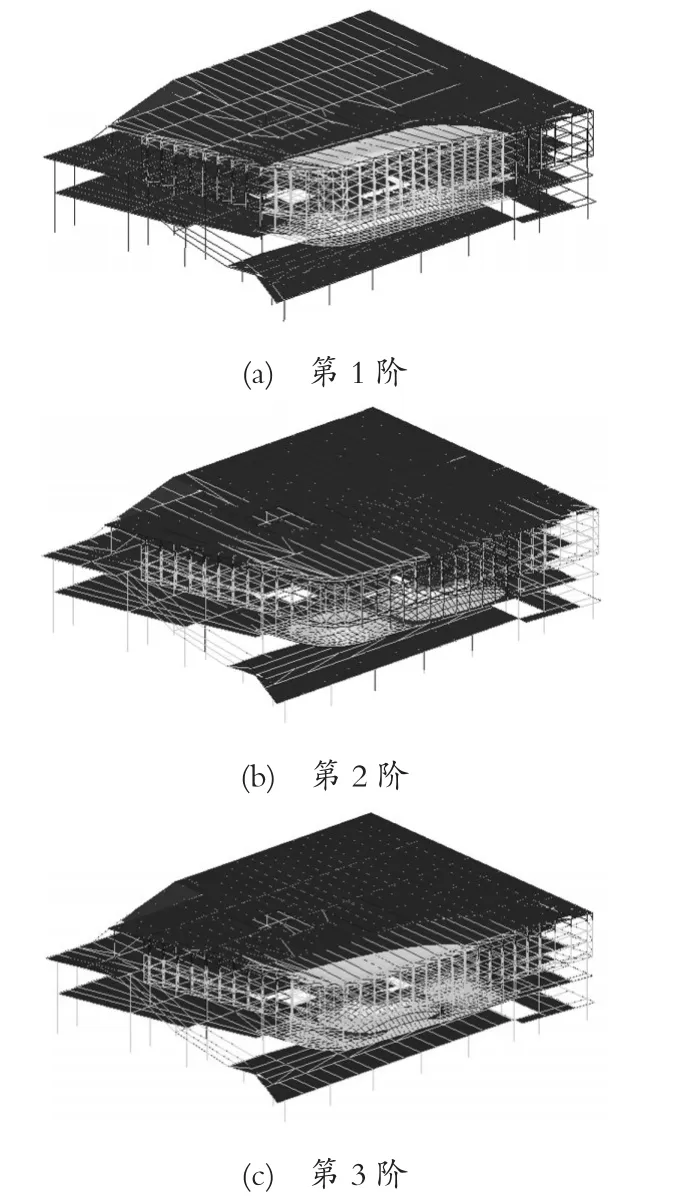
图2 悬挂板前3阶竖向振动时整体结构振型图

3 人行荷载模拟与工况定义

3.1 人行荷载的模拟

3.1.1 单人荷载

(1)单人步行及奔跑荷载

行人行走过程会产生竖向作用力、侧向作用力以及前进方向摩擦力，对于大跨结构来说，人群活动产生水平方向的作用力对楼盖结构影响较小，可以忽略不计，主要考虑人群活动对大跨结构产生的竖向产生的作用力。行人左右脚各行一步有一个近似的变化，即行人行走非常接近周期性运动，故可用傅里叶级数来描述单人行走步行力。

式中:Fp(t)为行人激励；fp为行人的步频；G为平均行人重量；t为时间；αi表示第i阶动荷载的初相位。

傅里叶级数n阶的取值与所要求的近似程度有关，一般认为，竖向荷载考虑前3阶已有足够的精度。通常采用IABSE(international association for bridge and structural engineering)荷载模型模拟竖向行人竖向步行力，如式(2)所示:

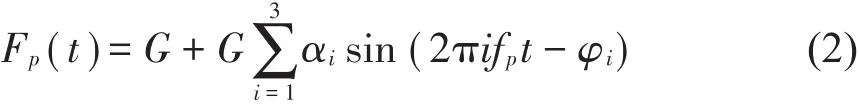
式中 :αi=0.4+0.25(fs-2)，α2=α3=0.1；φ1=0，φ2=φ3=π/2。图 3为单人按 2.0 Hz连续行走的荷载时程曲线。

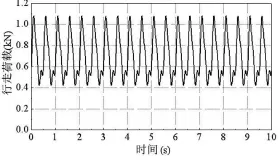
图3 单人连续行走荷载时程曲线

单人跑动荷载类似于单人步行荷载，仅步频较快，可近似认为按步行荷载模型公式(2)模拟，图4为单人按3.0 Hz连续跑动的荷载时程曲线。

(2)单人跳跃荷载

人体跳跃是包括起跳、腾空与落地三阶段的重复性运动过程，目前常用半正弦函数来描述单次跳跃曲线F(t):

图4 单人连续跑动荷载时程曲线

式中:G为平均行人重量，kp为跳跃动力因子，tp和Tp分别代表接触时间和一次跳跃总时间。

为简化分析，跳跃动力因子取1.5，简化后公式(2)为

将式(4)转化为连续跳跃荷载，可表示为

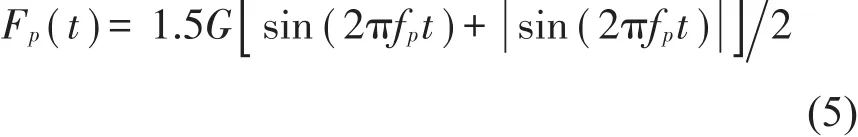
单人按2.70 Hz连续跳跃荷载时程曲线如图5所示。

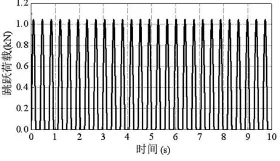
图5 单人跳跃荷载时程曲线

3.1.2 多人荷载

由于不同行人间的步频、相位、行走方向和行走位置等差异，多人荷载激励时，各人产生的振动激励会在一定程度上相互抵消。文献[5]假定人群行走为均匀分布人流，步频按正态分布，相位差在[0，2π]之间均匀分布，按随机变量方法做大量数据模拟。根据文献[5]，随机行走的多人荷载与单人荷载的关系。

当人群密度d＜1.0人/m2时，等效人数为:

式中，n为按人群密度计算的行人总数；ζ为人行桥阻尼比。

而人群密度d≥1.0人/m2，等效人数为:

3.2 工况定义

将多人荷载等效为同频同相位角均布荷载，并按照面积分配到悬挂板各节点上，利用有限元软件进行时程分析，求得悬挂板的响应。将多人荷载大致分为4类:连续行走、连续奔跑、小组行走和连续跳跃，表2以此列出悬挂板多人荷载工况。

(1)连续行走

文献[6]对非自由行走密度下的人群步行特征参数进行了统计，大量样本数据表明，人群步频均值随人群密度增大而降低。假设悬挂板随机走动行人密度适中(0.7人/m2)、拥挤(1.0人/m2)、较为拥挤(1.2人/m2)的情况，其对应的荷载频率分别为2.5 Hz、2.0 Hz和 1.8 Hz。

(2)连续跑动

跑动荷载频率较高，且单人跑动荷载类似于连续行走荷载，跑动频率也会随人群密度增大而降低。考虑随机人群在悬挂板上以2.7 Hz、3.1 Hz和3.5 Hz跑动，其密度分别为0.5人/m2、0.3人/m2和0.1 人/m2。

(3)小组行走

考虑7人同步频按1.75 H同步行走，以激发悬挂板第2阶振型幅值处位置共振。

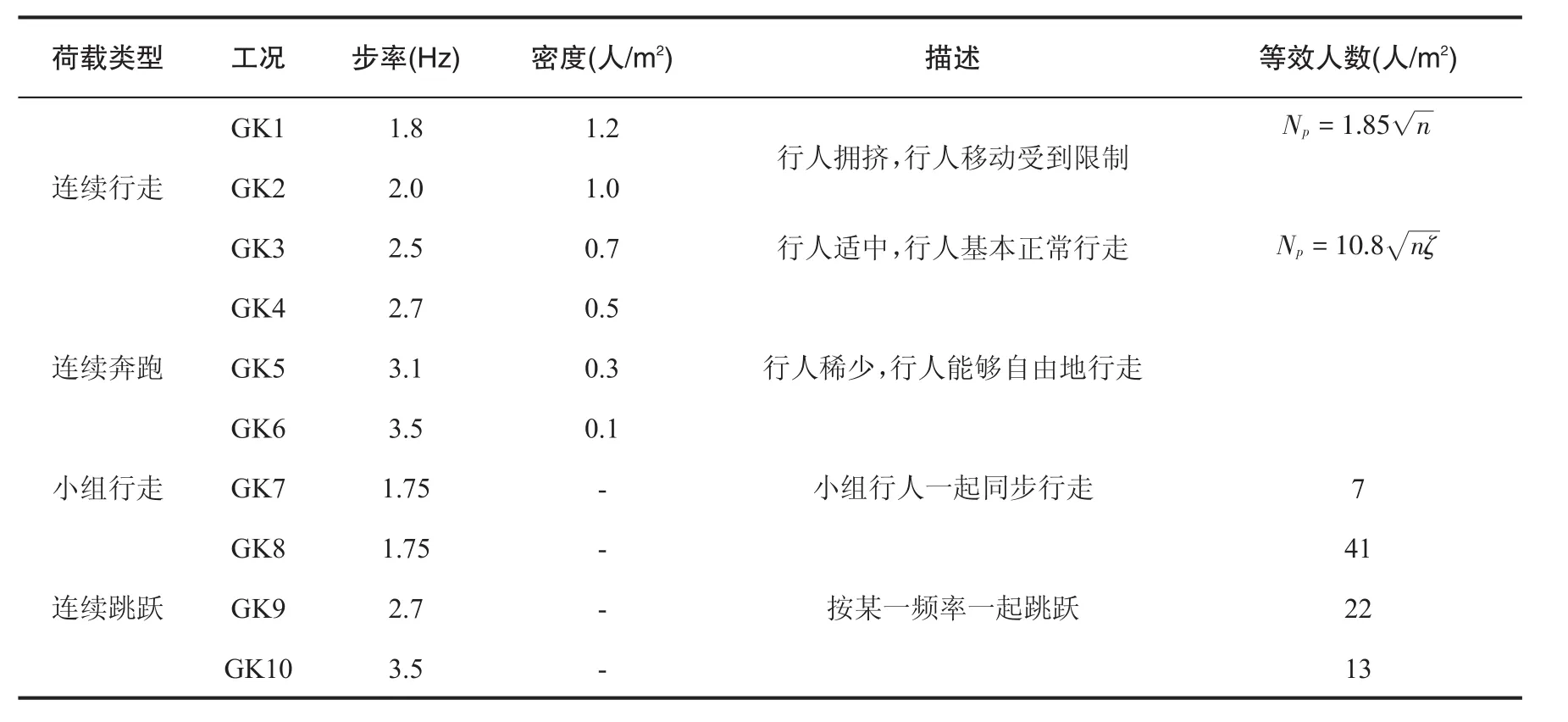
表2 人行荷载的定义

(4)连续跳跃

跳跃频率越高，两人同步跳跃难度越高。参考多人行走、跑动工况，考虑41人、22人和13人在悬挂板上同步以1.75 Hz、2.7 Hz和3.5 Hz跳跃的情况，以激发悬挂板竖向第1阶(2.72 Hz)和第2阶(3.50 Hz)振型幅值处位置共振。

4 悬挂板无控加速度响应

行人是振动激励荷载又是感受体，结构的位移响应、速度响应和加速度响应三者中，加速度能明显影响行人生理和心理感受，人体的舒适性感受可以采用振动加速度响应来评价。通常将振动加速度响应作为人体的舒适性感受控制指标。按照室内大跨度楼板竖向加速度限值规定[7]，人行荷载激励下悬挂板楼板竖向振动最大加速度峰值低于0.2 m/s2(见表 3)。

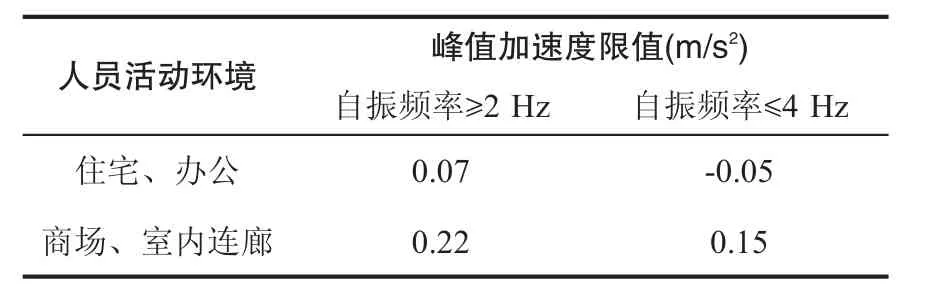
表3 楼盖竖向振动加速度限值

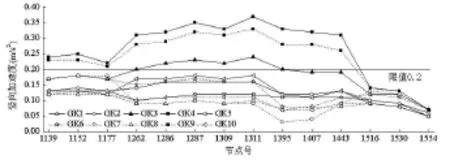
图6 各工况下悬挂板前6阶竖向振型幅值处节点加速度峰值响应

各工况下悬挂板前6阶竖向振型幅值处节点加速度峰值响应如图6所示，由图6可见，GK3、GK4和GK9工况行人荷载激励下悬挂板不满足悬挂板竖向振动加速度限值要求，其中悬挂板1阶竖向振型幅值处节点1311的竖向加速度峰值最大，依次分别为 0.24 m/s2、0.37 m/s2和 0.33 m/s2。原因在于GK3、GK7和GK9工况行人荷载频率接近悬挂板1阶竖向自振频率，导致悬挂板发生共振，从而使悬挂板竖向加速度响应大幅增加。同时，2阶振型幅值处节点1286、3阶振型幅值处节点1395、4阶竖向振型幅值处节点1287、5阶竖向振型幅值处节点1262和6阶振型幅值处节点1309等(见图7)在GK3、GK4和GK9工况行人荷载激励下加速度峰值也超过了舒适度限值要求，而2阶振型幅值处节点1152、3阶振型幅值处节点1530、4阶竖向振型幅值处节点1516、5阶竖向振型幅值处节点1177和6阶振型幅值处节点1554等节点加速度响应却低于舒适度限值，这说明节点1286、1395、1287、1262 和 1309 等节点加速度响应过大的主要因素并不是悬挂板竖向2～6阶振型共振造成的，而是由于这些节点比较靠近竖向1阶振型幅值处节点1311，因节点1311共振而加速度连带放大。

共振工况(GK4和GK9)行人荷载作用下悬挂板所有振型和仅1阶竖向振型下节点1311加速度时程曲线如图8所示，前20 s悬挂板受行人荷载激励，后15s行人荷载停止激励，悬挂板自由振动并衰减至静止。由图8可见，悬挂板仅考虑一阶竖向振型产生的加速度略小于考虑所有振型的。结合图6和图7可见，MTMD减振装置应根据悬挂板1阶竖向自振频率设计，并加装在悬挂板1阶振型幅值处节点1311附近的梁构件上。

5 悬挂板MTMD减振分析

5.1MTMD参数设计及加装位置

图7 悬挂板前6阶竖向振型幅值处节点

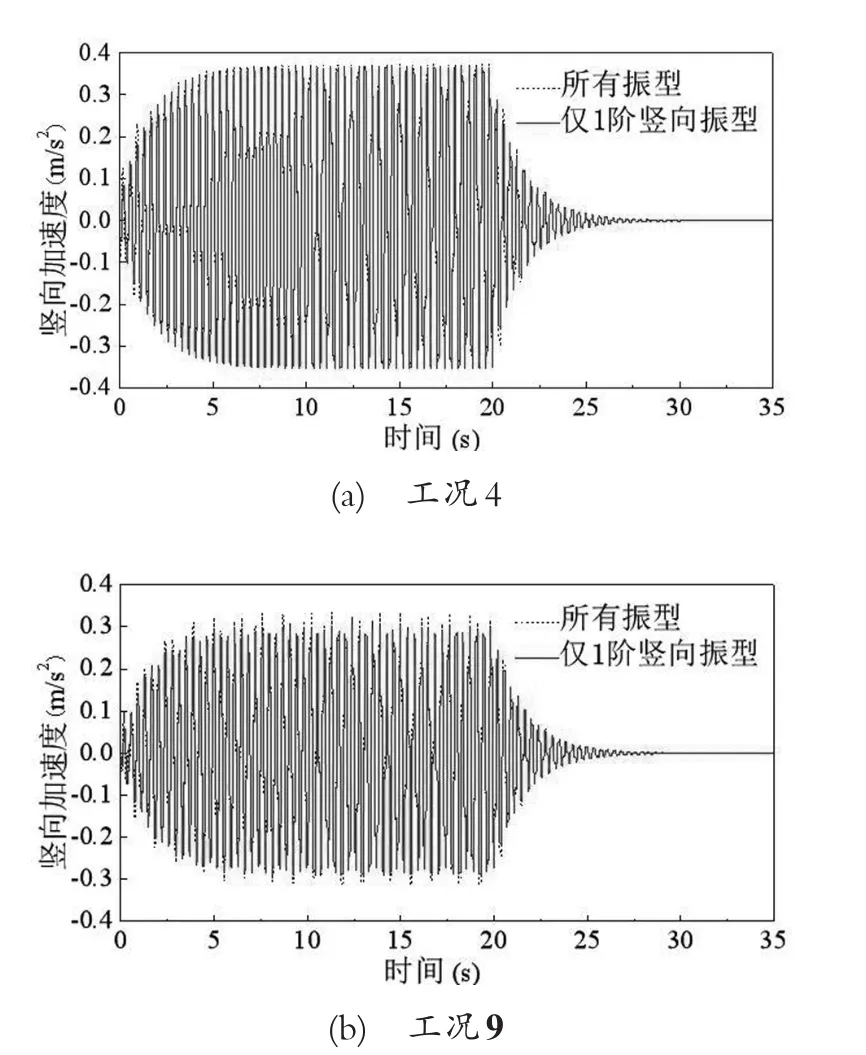
图8 悬挂板所有振型和仅1阶竖向振型下节点1311加速度时程曲线

为便于TMD制作与应用，假定MTMD系统中各TMD质量和阻尼比一致，TMD阻尼比按单个TMD的阻尼比取值[8]，见公式(8):

式中:ξ为TMD最优阻尼比；μ为TMD质量与结构质量之比。

同时，假定MTMD的频率对称分布于结构被控频率附近，每个TMD的频率计算公式为:

式中:fj为第j个TMD的频率；fs为结构被控频率；n为TMD的个数；β为MTMD的频率间隔。

确定各个TMD的质量md、阻尼比ξ和频率fj后，其刚度和阻尼见公式(10)、(11):

经过反复迭代，取6个质量为600 kg的TMD，悬挂板部分的质量为365.88 t，经计算每个TMD的质量比和阻尼比分别为0.00164和0.025，MTMD的频率间隔β取0.12 Hz，计算得到的MTMD刚度和阻尼如表4所示，图9节点1311周围6个高亮节点即是MTMD加装位置。

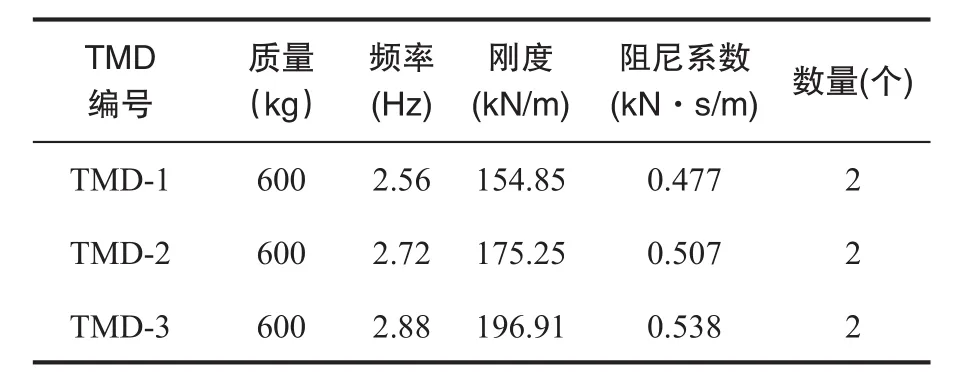
表4MTMD参数

5.2 悬挂板减振效果

减振前后，悬挂板1阶竖向振型幅值处节点1311在10种工况行人荷载激励下的减振加速度响应如图10所示。减振后节点1311在10种工况下加速度峰值均有所降低，且低于舒适度限值0.2 m/s2，尤其在工况4和工况9荷载激励下节点1311减振前后加速度峰值降低较其它工况降低明显。其主要原因在于MTMD是根据被控模态控制的，GK4和GK9工况行人荷载频率(2.7 Hz)接近被控模态频率(2.72 Hz)，激发MTMD发挥更佳优越地减振效果。

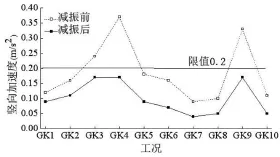
图10 各工况下节点1311的减振效果

GK3、GK4和GK9工况行人荷载激励下悬挂板前6阶竖向振型幅值处节点的减振效果如表4所示。由表4可知，在GK4、GK9工况行人荷载激励下，响应较大的振型幅值处节点1311、1286、1395、1287、1262和1309的减振效果均达43.8%以上，MTMD减振效果明显，这些节点主要是因为处于1阶竖向振型共振而加速度过大，MTMD根据悬挂板1阶竖向振型对应的频率和幅值处位置设置，因此在共振工况下MTMD减振性能良好。此外，图11为减振前后悬挂板1阶竖向振动振型图，由图可见，悬挂板上颜色形状变化明显，图中红色代表位移响应大，蓝色代表位移响应小，且除蓝色外其它颜色面积均有明显减小，说明在振型响应最大处设置MTMD是有效、合理的设计方法。

GK4和GK9工况行人荷载激励下悬挂板1阶竖向振型幅值处节点1331竖向加速度时程曲线如图12所示。节点1311受行人荷载激励后MTMD能够在1 s左右进入工作状态，迅速抑制节点1331的竖向加速度，并将其控制在0.2 m/s2以下，说明MTMD受激后既能够快速地进入工作状态，又能将悬挂板舒适度控制在限值内，从而很好地确保了悬挂板具有适宜的舒适度。