太赫兹辐射场下的石墨烯光生载流子和光子发射∗

2018-03-18陶泽华董海明段益峰

物理学报 2018年2期

陶泽华董海明段益峰

(中国矿业大学物理科学与技术学院,徐州 221116)

1 引言

石墨烯等二维半导体材料由于其独特的光电性质和应用,近年来得到了越来越广泛的关注和研究.石墨烯独特的光学和电子学属性,使得石墨烯非常适合制备高灵敏度的分子传感器和探测器[1,2].英国剑桥诺基亚研究中心研制并推出了在线版的超快石墨烯氧化物传感器,它拥有无与伦比的响应速度,是目前已知速度最快的湿度传感器.基于石墨烯隧穿效应的应力传感器具有可拉伸、高灵敏度、稳定性强、透明等特点,在人造皮肤、触摸屏以及电池电极等方面显示了巨大的应用潜力[3].美国伯克利大学的研究人员利用石墨烯制成了宽带、高速并且可以集成的光调制器[4].目前,特别引人关注的是石墨烯在电场控制下的发光和制备发光器件的研究取得了重大的研究进展.清华大学任天令教授领导的研究团队,利用氧化石墨烯和还原的氧化石墨烯的界面制备了光发射器件,实现了颜色可调发光二极管(LED)发光[5].北京理工大学的曲良体教授和他的团队利用水和石墨烯产生的电能点亮了LED灯泡,更为重要的是其转化效率高达62%[6].在二氧化硅衬底上施加偏压,石墨烯还可以发出中红外波段的光.Berciaud[7]和Freitag等[8]的研究表明,利用放置在衬底上的石墨烯可以在外加电场的调控下发射红外光.相关的研究还发现利用石墨烯可以实现超快的光子发射[9,10].

最近的研究表明,石墨烯也可以与其他半导体材料形成复合光电探测器,能够大幅提高探测器的光电响应速度和效率[11].石墨烯在可见光范围内具有普适的光电导[12],同时石墨烯具有高的光透射率[13]、超快光吸收饱和特性以及超高的太赫兹非线性光学性质[14].基于石墨烯-硅的异质结构中，石墨烯作为吸光材料吸收光，从而产生光生载流子,可以有效地提高光生载流子的寿命,并实现快速的光响应.这种基于石墨烯的探测器具有83 A/W的高响应率,以及600 ns的超快响应速度[15].西班牙的研究人员首次实现了互补金属氧化物半导体集成电路与石墨烯的单片集成,生产了基于石墨烯和量子点的数十万光电探测器组成的高分辨率图像传感器[16].韩国的研究人员第一次将石墨烯制成的电极成功集成在有机发光二极管面板衬底上,这种只有5 nm厚的石墨烯结构具有高度的灵活性、抗损伤性和高性能的特点.另外,采用自下而上的逐步热解法成功制备出了连续、均匀的硫掺杂石墨烯薄膜.以该薄膜为电极,采用微纳加工技术构建微型超级电容器[17].中国科学院包信和院士团队发展了一个基于石墨烯的三明治结构的平面超级电容器,实现了在一个基底上制造具有任意形状的超级电容器及其高度模块化集成[18].中国科学院苏州纳米研究所秦华研究员领导的团队成功获得了高灵敏度石墨烯太赫兹探测器,是迄今为止灵敏度最高的石墨烯太赫兹探测器[19].这些实验结果表明石墨烯在制备太阳能电池电极、光电探测器、光显示和发射等领域,尤其是太赫兹光电器件领域具有重要的应用价值.基于上述这些重要的实验发现,本文拟建立简洁有效的理论模型研究石墨烯的光生载流子和光子发射性质,这些性质是石墨烯最重要也是最基本的光电性质,研究可为石墨烯的光电器件的发展提供重要的基础.

2 理论模型

2.1 跃迁和发射概率

研究石墨烯-衬底(SiO2/Si)系统,该系统一个最重要的特点就是石墨烯的载流子浓度n0(电子或空穴)可以通过门电压Vg方便有效地线性调节,它们之间的关系是n0=7.2×1010cm−2/V·Vg[20].对于石墨烯系统,线性色散区的载流子的哈密顿量可以写为

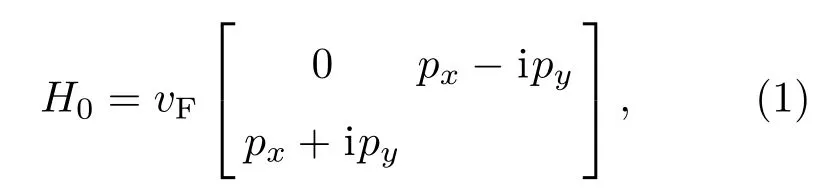
这里费米速度vF=108cm/s,px,py分别为动量p=−iħ∇在x轴和y轴上的分量.石墨烯低能量区载流子的运动可以由狄拉克方程描述,其本征能量和波函数分别为Eλ(k)=λγ|k|=λγk和ψλk(r)=|k,λ〉=2−1/2[1,λeiθ]eik·r,其中θ是k与x轴的夹角,γ= ħvF,ħk=p,r=(rx,ry).λ=±1分别表示导带(电子)和价带(空穴).当外加弱光场垂直入射到石墨烯表面时,光子与系统中的载流子相互作用,A(t)为辐射场矢势,采用库仑规范(∇·A(t)=0).取极化方向在x轴方向上的线性极化光场,利用p→p−eA(t),则石墨烯中载流子与光场的相互作用的哈密顿量为

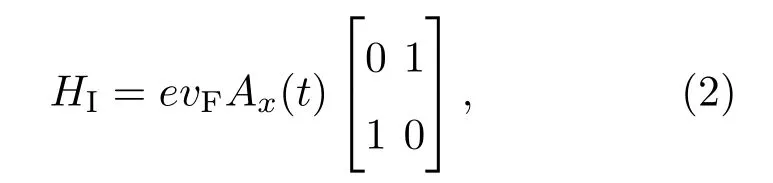
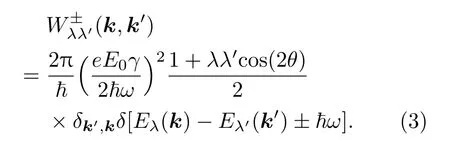
考虑太赫兹光场对石墨烯系统的作用,因太赫兹光子能量远远小于石墨烯中光学声子能量(196 meV),并且一般电子-声学声子散射为弹性散射,因此本研究不需要考虑电子-声子相互作用.

2.2 平衡方程理论

利用半经典的玻尔兹曼输运方程研究石墨烯对外场的响应.光场下的玻尔兹曼方程可以写为

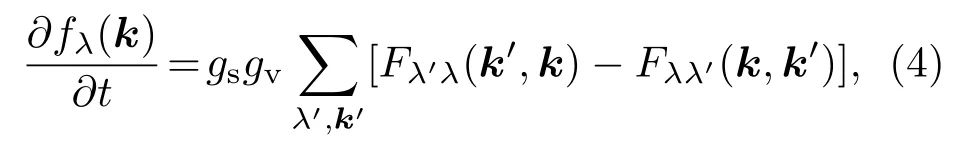
这里gs=2和gv=2分别表示自旋和能谷简并;fλ(k)是载流子的动量分布函数,而Fλ′λ(k′,k)=.直接求解该微分积分方程比较困难,可以通过平衡方程的办法求解[21].对上述方程两端同时乘以,分析该方程两端可以得出

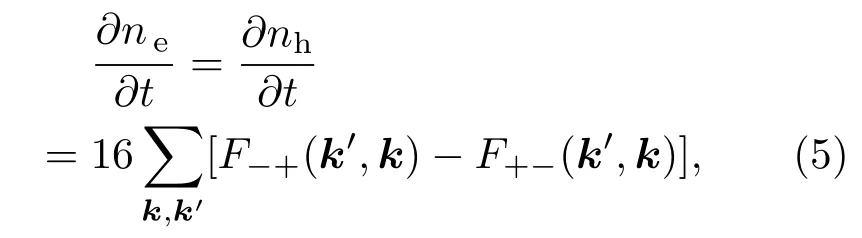
其中,ne和nh分别是导带中的电子浓度和价带中的空穴浓度.该平衡方程说明由于载流子电荷数守恒,光场的激发作用会使得价带中的电子吸收光子跃迁到导带从而留下空穴,导带中的电子会发射光子返回价带与空穴复合,而价带中的空穴的变化概率与导带中电子的变化概率是相同的.因此,当稳定状态时(dne/dt=dnh/dt=0),积分可以得到稳定状态下的平衡方程:

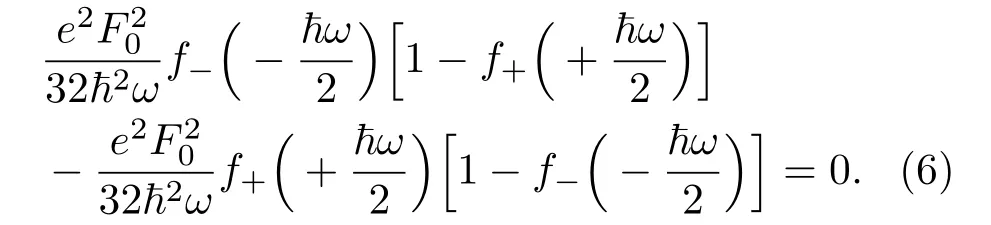
同时,稳定状态时由于光子吸收和发射导致的光场与载流子之间的能量转移率分别为

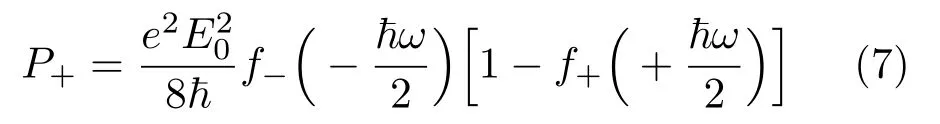
和

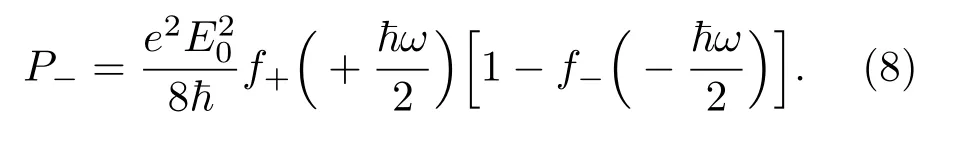
2.3 太赫兹光生载流子

通常情况下,考虑电子型(n型)掺杂的石墨烯系统.在没有外场时,载流子为导带中的电子,其电子掺杂浓度为n0,该浓度可以通过门电压Vg方便连续地调节.在外加光场时,石墨烯的价带中的电子会吸收光子而跃迁到导带,价带中留下相应的空穴,这部分由于光子的激发而新产生的导带中的电子或价带中的空穴就是光生载流子,其浓度为n.导带中的一部分电子也会发射光子从导带返回价带与空穴复合,空穴浓度为nh.由载流子电荷数守恒可知nh=n,ne为导带中总的电子浓度,则

其中

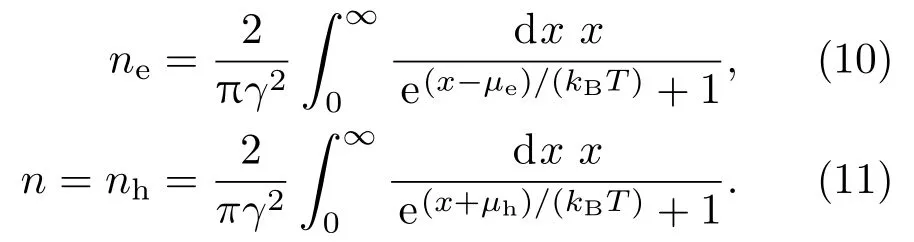
通过动量平衡方程(6)和载流子电荷守恒方程(9),可以自洽计算出任意光场和掺杂浓度时导带中电子的化学势µe和价带中空穴的化学势µh,从而也就可以确定光生载流子浓度n.一般非简并情况下,可以将费米分布函数近似为玻尔兹曼分布函数,进而可以求解方程组(6)和(9),从而得到光生载流子的解析解,即

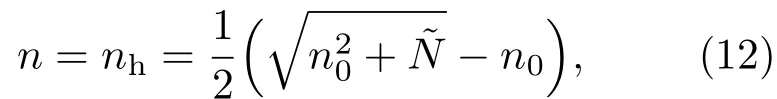
2.4 太赫兹光子发射率

通过能量转移率方程(7)和(8),以及自洽计算可以计算得出导带中电子的化学势µe和价带中空穴的化学势µh.在此基础上可以计算得到导带中的电子返回价带与空穴复合,同时辐射光子,相应的光子发射率为ε(ω).同样,将费米分布函数近似为玻尔兹曼分布函数,得到一个简洁有效的解析解,即

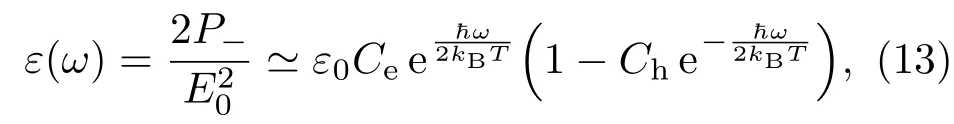
其中ε0=e2/(4ħ),,.本征的石墨烯是无带隙的半金属狄拉克系统,因此不能形成稳定的激子,光子发射率ε(ω)是由导带中的电子返回价带而直接发射产生的光子.

3 结果与讨论

图1给出了不同掺杂浓度n0时,室温下光生载流子浓度的相对产生率n/n0随太赫兹光子频率的变化.从图1可以看出,随着入射光子频率的增加,光生载流子的产生率会迅速增大.这是因为,当光与载流子相互作用时,需要满足能量守恒.光子频率越大,光子的能量就越大,这样就可以使越来越多的价带中的电子吸收光子而跃迁到导带.图1结果表明,石墨烯的掺杂浓度n0越小,光生载流子的浓度就会越大.根据泡利不相容原理,掺杂浓度越高,相应的价带中的电子就需要吸收更大能量的光子才可以跃迁到导带产生光生载流子n.因此,掺杂浓度越高,光生载流子的产生就越困难.通过(12)式,可以非常方便地给出不同温度和太赫兹光子频率对应的光生载流子浓度,该公式对于研究以及应用石墨烯的光电性质非常有意义.通过(12)式可知,掺杂浓度n0越小,光生载流子浓度n就越大,当n0→0时,;反之n0越大,n就越小;当时,n=nh→0,即电子无法吸收光子产生光生载流子.这是由于当n0越大,其对应的电子的费米能量EF就会大于光子的能量ħω.一般情况下,只有ħω＞EF时,才会产生明显的光生载流子.如前所述,石墨烯-衬底系统的一个重要优势是可以通过门电压非常方便地调节控制该系统的载流子的掺杂浓度.因此,可以通过门电压调控石墨烯的载流子浓度,从而根据需要非常方便地调节该系统的光生载流子浓度.典型的1 THz频率的入射光子,对应的光子能量为4.2 meV,由费米能量可知,对应的电子密度为ne=1.3×109cm−2.因此,当入射光子频率为1 THz时,电子的掺杂浓度小于1.3×109cm−2时,能够产生明显的光生载流子;否则不能够产生明显的光生载流子.

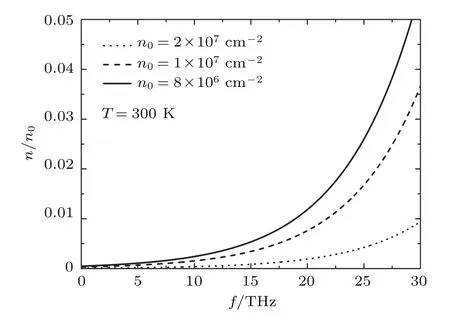
图1 不同掺杂浓度n0时,室温下光生载流子的相对产生率n/n0随太赫兹光子频率的变化Fig.1.Photon excited carriers n over terahertz frequency f for the different doped electron densities n0 in room temperature.

图2计算了固定掺杂浓度n0,不同温度T时,光生载流子的相对产生率n/n0随太赫兹光子频率的变化.如图2所示,随着入射光子频率的增加,光生载流子的产生率会迅速增大.同时,计算结果表明掺杂浓度n0一定时,温度T越低,光生载流子的产生率就越大.光生载流子的产生率与光的吸收率成正比.在发生光吸收时,价带的电子吸收光子跃迁到导带,因此价带电子的占据概率f−(k)越大,导带中电子占据概率f+(k)越小,则光吸收率就越大,对应的光生载流子产生率也就越大.当温度变低时,石墨烯中价带电子的占据概率以及相应的导带中空态的概率会变大,因而就会观察到温度T越低、光生载流子的产生率越大的现象.同时,通过(12)式分析可知,温度越小,eħω/(kBT)就越大,˜N也就越大,因而光生载流子浓度n就越高.典型的1 THz频率的入射光子,对应的热涨落为5kB,因此,当入射光子频率为1 THz、温度超过5 K时,热涨落能够明显地影响石墨烯系统的光生载流子.同时也可以看出,温度对石墨烯的太赫兹性质有较大的影响.

图2 固定掺杂浓度n0,不同温度T时,光生载流子的相对产生率n/n0随太赫兹光子频率的变化Fig.2.Relative Photon excited carriers n/n0over terahertz frequency f for the different temperatures T at a fi xed n0.

图3 T=200 K,不同掺杂浓度n0时,光子发射率ε(ω)随太赫兹光子频率的变化Fig.3. Photon emissivity ε(ω)over terahertz frequency f for the different doped electron densities n0 at T=200 K.

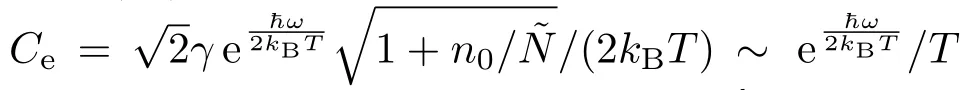
图4 不同温度T、一定掺杂浓度n0时,光子发射率ε(ω)随太赫兹光子频率的变化Fig.4. Photon emissivity ε(ω)over terahertz frequency f for the different temperatures T at a fi xed n0.

4 结论

基于最近的一系列重要的实验发现,建立了半经典的自洽理论方法,研究了石墨烯系统的光生载流子和光子发射率.通过分析得到了石墨烯太赫兹光场下的光生载流子浓度和光子发射率的解析表达式,该表达式对石墨烯光电材料和器件的发展具有重要的应用价值.研究发现,石墨烯掺杂电子浓度(门电压)越小,系统温度越低,光生载流子浓度越大;电子掺杂浓度(门电压)越高,系统温度越低,光子发射率越高.通过改变门电压,可以有效地调节和控制石墨烯光生载流子和光子发射.这些理论结果对发展以石墨烯为基础的光电器件具有重要的参考价值.

[1]Yuan W J,Shi G Q 2013J.Mater.Chem.A1 10078

[2]He Q Y,Wu S X,Yin Z Y,Zhang H 2012Chem.Sci.3 1764

[3]Dolleman R J,Davidovikj D,Santiago J 2016Nano Lett.16 568

[4]Liu M,Yin X B,Erick U A 2011Nature474 64

[5]Wang X M,Tian H,Mohammad M A 2015Nature Commun.6 7767

[6]Zhao F,Liang Y,Cheng H H,Jiang L 2016Energy Environ.Sci.DOI:10.1039/C5EE03701H

[7]Berciaud S 2010Phys.Rev.Lett.104 227401

[8]Freitag M,Chiu H Y,Steiner M,Perebeinos V,Avouris P 2010Nature Nanotech.5 497

[9]Lui C H,Mak K F,Shan J H 2010Phys.Rev.Lett.105 127404

[10]Brida D 2012Nature Commun.4 1987

[11]Tao L,Chen Z,Li X,Yan K,Xu J B 20172D Mater.Appl.1 19

[12]Kuzmenko A B,van Heumen E,Carbone F,van der Marel D 2008Phys.Rev.Lett.100 117401