离子推力器推力密度特性∗

龙建飞 张天平 杨威 孙明明 贾艳辉 刘明正

(兰州空间技术物理研究所,真空技术与物理重点实验室,兰州 730000)

1 引 言

离子推力器具有高比冲、高精度等特点,是一种先进的航天器动力装置[1,2].国内自主研发的20 cm口径离子推力器(LIPS-200)已于2012年10月成功进行首次飞行试验[3],2017年4月该推力器搭载实践十三卫星进入太空,主要应用于卫星的南北位置保持任务,实现了首次空间应用.在空间应用中,离子推力器的推力作为重要的性能指标而备受关注,准确计算出推力并得到推力密度分布,对离子推力器性能评价具有重要作用[4],同时也将为卫星的轨道设计提供支持.

离子推力器通过栅极产生加速电场,将放电室内等离子体中的离子聚焦、加速、引出并形成束流,从而产生推力[5],其中单位面积上产生推力称为推力器的推力密度[6].目前多采用经验模型对离子推力器的总推力进行计算.1984年Brophy和Wilbur[7]建立了离子推力器性能零维模型,其中推力为为推进剂质量流量,为束流离子平均速度.此后,Takao等[8],Goebel等[9]以及Kitamura等[10]分别从束流发散角和双荷离子等因素对经验模型进行了修正.修正后的推力表达式为,式中,α为双荷离子补偿系数,β为束流发散角因子,e为电子电荷,Vsc为屏栅电压,mi为离子质量,Ib为束电流.根据推力器工作参数,并通过束流诊断实验数据估算出修正因子α和β,便可以计算出推力器的总推力.在此基础上,将总推力除以推力器出口面积,进一步可以估算出推力器的平均推力密度.

另外,研究人员在推力器的推力密度提升方面也开展了相关研究.Hruby等[11]采用C60簇作为离子推力器的推进剂,通过增加离子质量来提高离子推力器的推力密度;Bramanti等[12]以及Walker和Bramanti[13]开展了四栅极技术研究,通过增大加速电压来提高束流离子的喷出速度,相比传统的两栅极技术,四栅极技术可以显著增大推力器的推力密度.

上述研究工作在离子推力器总推力的理论计算方面取得了丰硕的成果,同时在提高推力器的平均推力密度设计方面也开展了卓有成效的研究.由于不同栅孔引出的束流离子数量和速度均存在差异,进而导致了离子推力器的推力密度具有非均匀特性,即采用平均推力密度很难准确反映出离子推力器的真实推力密度特性,目前关于离子推力器的推力密度分布研究少有报道.

本文采用粒子模拟-蒙特卡罗碰撞(particlein-cell-monte carlo collision,PIC-MCC)方法对离子推力器推力密度分布进行研究.建立离子推力器的推力微观表达式,对栅极系统单孔束流引出进行仿真,通过统计束流离子喷出数量和速度等微观参数,进而直接计算出单孔推力,结合放电室等离子体密度径向分布,扩展得到推力器的总推力;进一步研究束流多组分粒子对推力的影响以及推力密度分布特性,分析并讨论结果,最后开展实验验证.

2 计算模型

2.1 推力密度表达式

离子推力器主要通过栅极将放电室等离子体中的离子聚焦、加速、引出,形成束流并产生推力.由于栅极是由上千个小孔组成,因此,推力器的总推力等于各栅孔束流产生的推力之和.栅孔束流产生推力表达式为[14]

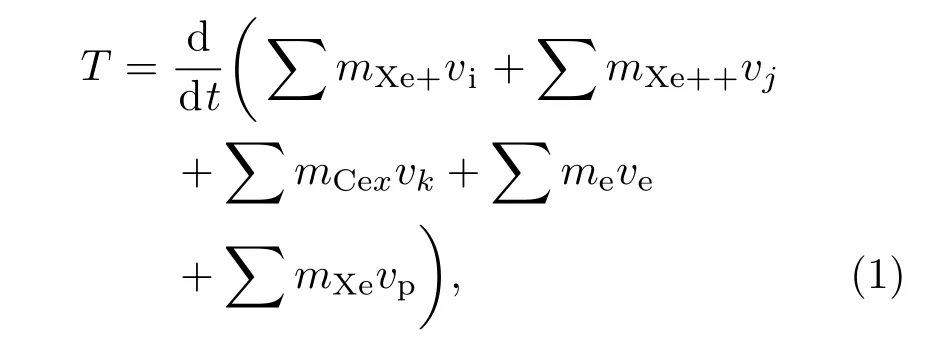
由于电子质量远小于离子质量,使得其动量远小于离子动量,同时原子不受电场加速,对应速度增量很小而被忽略.因此,推力计算中只考虑各类离子动量,

从上面表达式可以看出,推力器产生的推力等于单位时间喷出各类离子动量之和.由于喷出离子的速度存在差异,运用宏观的平均速度进行表征将给推力计算带来误差.相比而言,采用数值模拟方法,记录单位时间推力器所有喷出离子的数量和轴向速度等微观参数,进而可更加准确地计算出推力.

进一步得到推力密度f的表达式为

式中,r为相邻两栅孔中心之间距离.

2.2 束流引出数值模型

离子推力器主要通过栅极来实现束流离子的加速和引出,栅极为布满上千小孔的拱形曲面结构,由于上千小孔同时仿真计算量过大,因此,一般采用单孔进行数值仿真.

2.2.1 计算区域

计算区域如图1所示,图中左边为栅极组件俯视示意图,中间为栅极组件的剖面图,黑色部分代表栅极(包括屏栅和加速栅),右侧为选择的二维计算区域.由于栅孔具有轴对称性,因此选取一个孔的中心线作为计算区域的边界,计算区域垂直方向上的大小取为两相邻栅极孔中心间距的1/2,计算区域的左边界位于屏栅上游放电室内,右边界位于加速栅极下游区域.

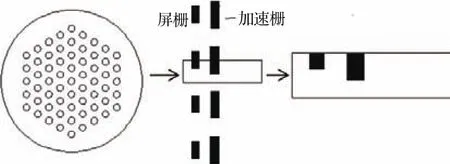
图1 计算区域示意图Fig.1.Schematic of calculation area.

2.2.2 PIC-MCC模型

针对离子推力器栅极束流引出过程开发了PIC-MCC仿真程序,目前已经在离子推力器羽流研究中得到较好的应用[15].该程序主要过程描述如下:首先对计算区域采用正交等距法进行网格划分,采用面积权重法将带电粒子电量权重到周围网格节点,通过求解泊松方程计算各节点电势和电场,根据周围节点电场对粒子所在位置的电场强度进行插值,运用牛顿第二定律对粒子进行加速,对不同边界处的粒子进行处理,再用新的粒子位置求解新的电场分布,上述过程循环进行,当计算区域所有节点电场变化小于0.05%时认为程序达到收敛.离子与原子之间的动量碰撞和电荷交换碰撞均采用MCC方法进行处理,其中新产生的交换电荷离子直接耦合到PIC模块计算中,而失去电荷的离子将被删除.仿真计算流程如图2所示.

图2 仿真流程图Fig.2.Flow chart of simulation.

针对该数值模型的主要过程做进一步详细说明.PIC模块中,每个时间步长都有放电室离子从左边界进入,进入的离子少部分被栅极截获,大部分从右边界喷出,进而可实现计算区域内离子总数量的平衡.离子入射数量满足Child-Langmuir定律,即每个时间步从左边界进入计算区域的离子数ΔNin为[16]

式中,n0为放电室出口离子密度,k为玻尔兹曼常数,Te0为放电室电子温度,rsc为屏栅孔半径.

计算区域内电子密度按照Boltzmann分布处理.屏栅孔及上游区域内电子密度表示为[17]:

式中,Φ为电子所在位置电势,Φu为放电室电势.在加速栅下游区域,电子密度可以表示为:

式中,n∞,Φ∞,Te∞分别为栅极下游中和面的电子密度、电势以及电子温度.

电场根据泊松方程求解,

式中,ε为真空介电常数,ni和ne分别为计算区域离子密度和电子密度.泊松方程求解采用有限差分法,所使用的格式为中心差分五点格式.为了提高电场计算收敛的速度,本文中采用逐次超松弛(SOR)方法求解.

带电粒子运动满足牛顿-洛伦兹力定律:

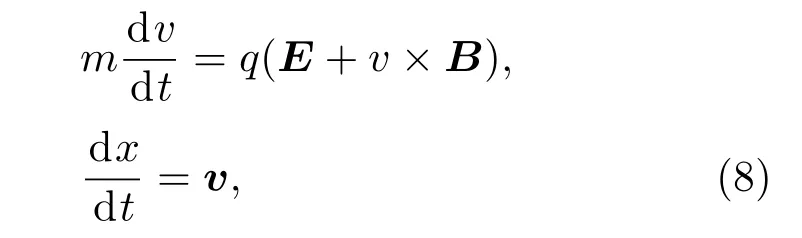
式中,v为粒子速度,q为粒子电量,x为粒子位置,E和B分别为粒子所在位置处的电场强度和磁场强度.

计算区域中边界处理如下:左边界为流入边界,右边界为流出边界,模拟粒子从左边界进入,经过栅极间的电场加速后从右边界离开,当模拟粒子撞到栅极上时将被删除;上边界和下边界都为对称边界,从下边界反射回来的模拟粒子相当于栅极孔的未模拟的另一半区域中的粒子进入到计算区域,同样,从上边界反射回来的模拟粒子相当于相邻的栅极孔中引出的粒子进入到计算区域.

MCC模块主要处理粒子间的碰撞,包括离子和原子之间的电荷交换碰撞和弹性碰撞.电荷交换碰撞(charge exchange collision,CEX)为快速离子与慢速原子发生电荷交换碰撞,该过程可以表示为[18]:

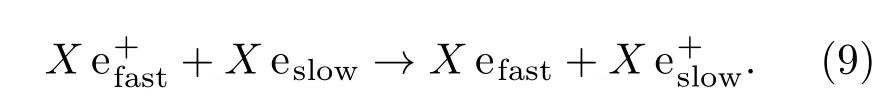
单个时间步长内,离子与所处空间位置的中性原子发生碰撞概率P为

式中,σt为碰撞截面,nn为原子密度,vi-n为相对速度,Δt为时间步长.模型中碰撞截面借鉴文献[19].

由(10)式计算出电荷交换离子产生概率后,利用程序本身产生的0—1之间的随机数ran,当ran＜P时即认为发生电荷交换碰撞,生成了电荷交换离子.为了避免每次程序重新运行产生相同的随机数,编程时引入了系统时间作为产生随机数的种子,这就保证了每次程序重新运行都产生不同的随机数.

3 仿真结果与验证

选取兰州空间技术物理研究所自主研发的LIPS-200离子推力器为研究对象,以该推力器额定工况运行参数作为模型输入条件,如表1所列.

表1 LIPS-200推力器主要参数Table 1.Main parameters of LIPS-200 thruster.

根据给出的参数和条件进行仿真计算,当程序满足收敛精度时达到稳定,对粒子微观参数进行统计并输出计算结果.模拟中,程序稳定状态下粒子总数约400000个,其中电荷交换离子数约2300个.

3.1 束流仿真

以栅极中心(r=0 mm)单孔束流引出为例进行仿真计算,其输入条件为放电室出口离子密度,约为2.66×1017m−3[15],仿真结果如图3所示.图3(a)电势分布仿真结果显示,计算区域内电势径向变化很小,主要沿着轴向变化.电势在靠近放电室出口处达到最大,约为1000 V,在屏栅与加速栅之间电势出现快速下降,而加速栅之后电势变化趋于稳定.图3(b)等离子体密度仿真结果显示,离子密度沿径向分布主要在栅孔轴线附近,靠近栅极附近离子密度很小(加速栅附近几乎没有离子).沿着轴向方向,离子密度从左边界逐渐减少,临近右边界时趋于稳定.仿真结果表明,束流离子具有较好的聚焦、加速和引出等特性.

图3 单孔束流引出仿真结果 (a)电势分布;(b)离子密度分布Fig.3.Simulation results of beam extracted:(a)Potential distribution;(b)ion density distribution.

3.2 单孔推力计算

为了准确计算出推力,根据推力微观表达式(2)式,分别对束流中的单价离子、双荷离子、CEX离子的喷出速度和喷出数量进行统计与计算.

图4为单孔束流中粒子喷出速度的统计结果.模型中共选取2000组样本,分别对单价离子、双荷离子以及CEX离子的轴向喷出速度进行统计.结果显示,单价离子轴向喷出速度主要在36000—36800 m/s范围(约96%),双荷离子轴向喷出速度主要在51000—52000 m/s范围(约97%),CEX离子轴向喷出速度为11000—28000 m/s.进一步计算可以得到:单价离子轴向喷出平均速度为36486 m/s,双荷离子轴向喷出平均速度为51591 m/s,CEX轴向喷出平均速度为19182 m/s.相比而言,单价离子和双荷离子的轴向喷出速度较为集中,而CEX离子轴向喷出速度较为分散.

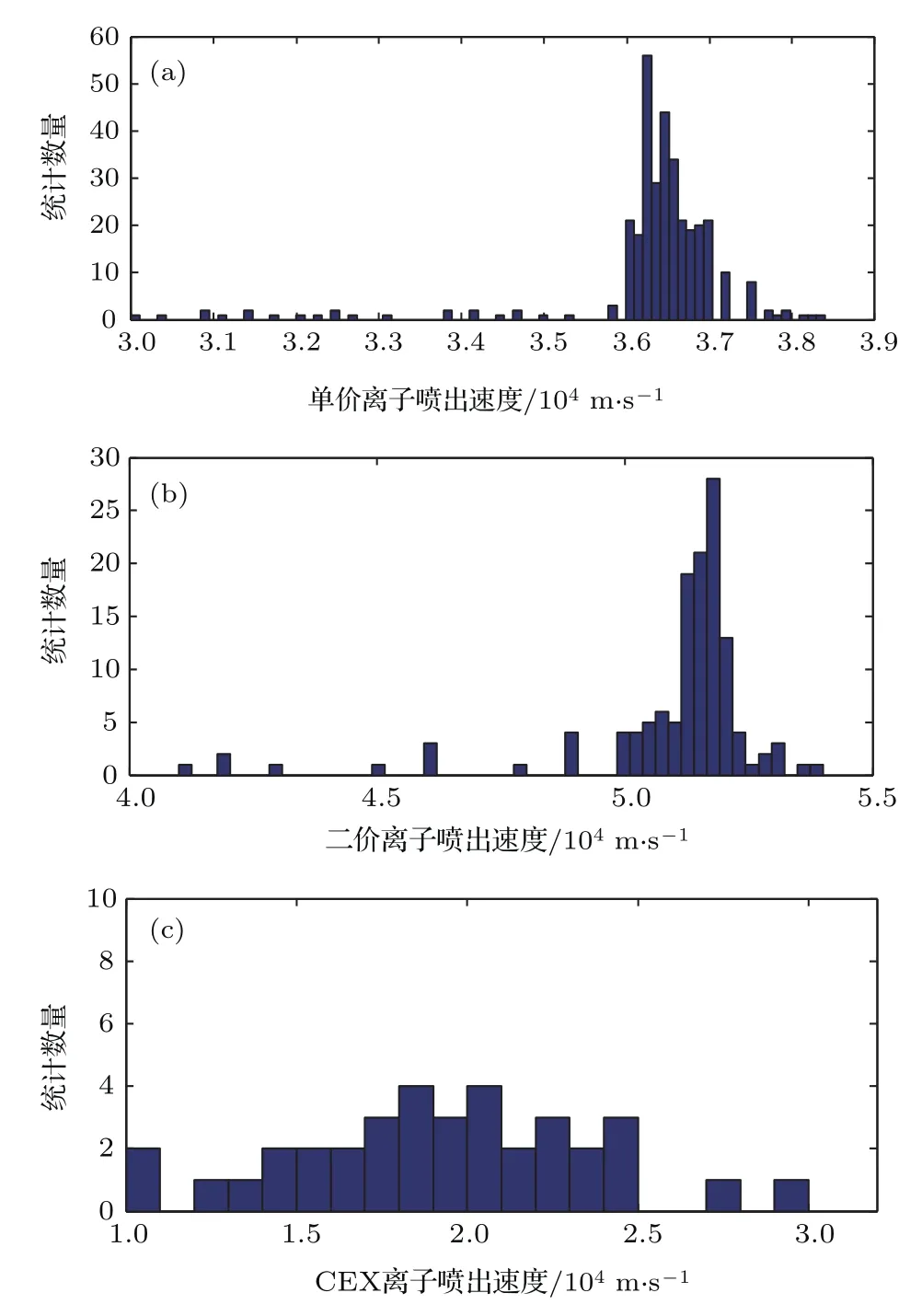
图4 喷出粒子轴向速度统计 (a)单价离子;(b)双荷离子;(c)CEX离子Fig.4. Statistics of axial velocities for particles ejected:(a)Singly charged ion;(b)doubly charged ion;(c)CEX ion.

离子喷出轴向速度vout满足如下公式:

式中,v0为离子初始速度,qi为离子电量,Vsc为屏栅电压,mi为离子质量,Δv为束流离子在加速过程由于非弹性碰撞产生能量损耗导致的速度减少量.

对束流离子喷出速度分析可知,离子初始速度一般按玻姆速度处理[15],约为几电子伏;而栅极系统中屏栅电压一般超过1000 V,同时束流引出过程中非弹性碰撞造成的能量损耗几乎可以忽略.因此,束流离子喷出速度主要受屏栅电压影响.当屏栅电压固定时,单价离子和双荷离子的喷出速度较为集中.由于双荷离子电荷是单价离子的2倍,可以获得2倍于单价离子的加速能量,其对应的喷出速度大约为单价离子的倍.CEX离子主要在束流引出过程中产生,由于不同产生位置所获得的加速电压不同,因此,CEX离子的喷出速度范围较广.

图5为单孔束流中粒子喷出数量的统计结果.模型中统计了20个时间步长的喷出粒子数量,从图中可以看出,喷出粒子数量随时间变化不大,仿真结果具有较好的稳定性.统计结果表明:束流中单价离子喷出数量约为9.98×1014s−1,双荷离子数量约为1.13×1014s−1,CEX离子数量约为0.38×1014s−1.进一步计算可以得到束流成分中单价离子、双荷离子以及CEX离子所占比例分别约为86.85%,9.83%和3.31%.

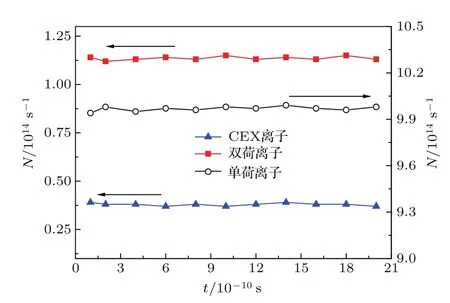
图5 喷出粒子数量统计Fig.5.Number of particles exhausted from thruster.

放电室内等离子体中的单价离子、双荷离子被栅极引出过程中,少部分将被屏栅、加速栅截获,另有少部分将与空间中的原子发生电荷交换碰撞,产生新的CEX离子,绝大部分将被喷出形成束流.因此,喷出离子数量ΔNout满足如下公式:

式中ηs为离子透过率.

从上面的公式可以看出,喷出离子数量主要与入射离子数量和离子透过率相关.根据(4)式可知,在栅极结构及工作参数固定的情况下,入射离子数量取决于放电室出口的离子密度.离子透过率为栅极喷出离子数量与从放电室引入离子数量的比值,该参数是屏栅透过率和加速栅透过率综合作用的结果,当栅极系统具有较好的聚焦特性时(即不发生过聚焦和欠聚焦),离子透过率主要与栅孔电流相关.研究表明[20],随着栅孔电流增大,屏栅透过率呈现出先缓慢减小后迅速减小的趋势;加速栅透过率随着栅孔电流增大,先缓慢上升后快速减小.电荷交换碰撞过程中,由于双荷离子速度相对较快,且双荷离子产生的电荷交换碰撞截面小于单价离子,因此,束流引出过程中主要为单价离子与原子发生电荷交换碰撞,即CEX离子主要由单价离子转换而来.

根据统计数据,结合推力微观参数表达式(2)式,即可以直接计算出单孔束流产生的推力,约为9.37×10−3mN.束流推力是所有离子共同作用的结果,结合离子微观参数分析可知,离子喷出数量主要与放电室出口处的离子密度、离子透过率密切相关,同时不同离子的喷出速度具有较大差异,使得束流产生推力的过程具有较大的复杂性,进而给推力计算带来困难.

3.3 束流组分对推力影响

表2为束流多组分粒子产生的推力的计算结果.通过对单孔中多组分粒子产生的推力进行求和,分别获得了单价离子、双荷离子和CEX离子产生的总推力.结果显示,单价离子产生的总推力为7.93×10−3mN,双荷离子产生总推力为1.27×10−3mN,而CEX离子产生总推力为0.17×10−3mN.

表2 单价离子、双荷离子、CEX离子产生推力Table 2.Thrust generation of singly charged ion,doubly charged ion,and CEX ion.

图6为推力器中不同束流离子产生的推力贡献比.从图中可以看出,单价离子产生的推力贡献比最大,约为84.63%;其次是双荷离子,所占比例约为13.55%;而CEX离子产生的推力仅为1.82%.由于双荷离子可以获得较高的喷出速度,在相同喷出数量下,可以比单价离子产生更大的推力,从而提高推力密度.但是高能量的双荷离子会对加速栅造成严重溅射,使得推力器的寿命显著下降[21],因此,需要有效控制束流中双荷离子的比例.电荷交换碰撞产生的离子速度较慢,由于慢速离子在二次加速过程中只能获得部分加速能量,从而产生的推力也较小,因此需要尽量避免.减少电荷交换碰撞的主要途径包括:增大放电室推进剂利用率以及提高真空背景压强,降低束流中性原子密度从而降低电荷交换碰撞概率,最终提高推力密度.

图6 不同束流离子推力贡献比Fig.6.Thrust contribution ratio of charge particles in beam.

3.4 推力密度分布

为准确获得不同径向位置处栅孔引出束流中离子的数量和速度等微观参数,需要对放电室出口处的离子密度分布进行估算.文献[22]研究表明,环尖场离子推力器中放电室出口(屏栅上游)处离子密度分布与束流离子密度分布具有相近的分布规律.因此,通过测试推力器的束流密度[23],可以近似得到放电室出口处的离子密度分布规律.LIPS-200离子推力器放电室出口的离子密度分布如图7所示.从图中可以看出,放电室出口的离子密度具有较好的中心轴对称性,在径向位置约±0.05 m处离子密度出现快速下降.放电室离子密度分布主要影响因素包括磁场、结构、供气等参数.

LIPS-200离子推力器束流平直度为0.6[24],可以计算出放电室出口处最大的离子密度约为2.66×1017m−3,结合图7的分布规律,可以得到放电室出口不同径向位置处的离子密度.

图7 放电室出口离子密度分布Fig.7.Ion density distribution at the exit of the discharge chamber.

图8为LIPS-200推力器推力密度的径向分布.将放电室出口的离子密度分布作为不同径向位置栅孔的输入条件,通过数值仿真模型依次计算出沿径向各单孔的推力密度,进而得到推力器的推力密度分布.计算结果显示,推力密度沿径向分布具有较好的中心轴对称性,在推力器中心有最大推力密度约0.19 mN/cm2,推力密度在径向位置约为±0.055 m处出现快速下降之后趋于平稳,放电室边缘处有最小推力密度约为0.01 mN/cm2,其中平均推力密度约为0.12 mN/cm2.

图8 推力密度分布Fig.8.Distribution of thrust density.

图9为推力密度分布与放电室出口离子密度分布的比较.通过对推力密度和离子密度进行归一化处理,从图中看出两者分布较为相近.分析认为,由于离子获得能量主要来自于栅极电压,不同栅孔喷出粒子平均速度相差很小[25],即造成栅孔推力差异主要来源于喷出粒子的数量.同时在栅孔具有较好透过率的情况下(不产生过聚焦和欠聚焦),栅孔喷出粒子数量主要取决于放电室出口离子密度分布.因此,推力器的推力密度分布与放电室出口离子密度分布具有相近的关系.

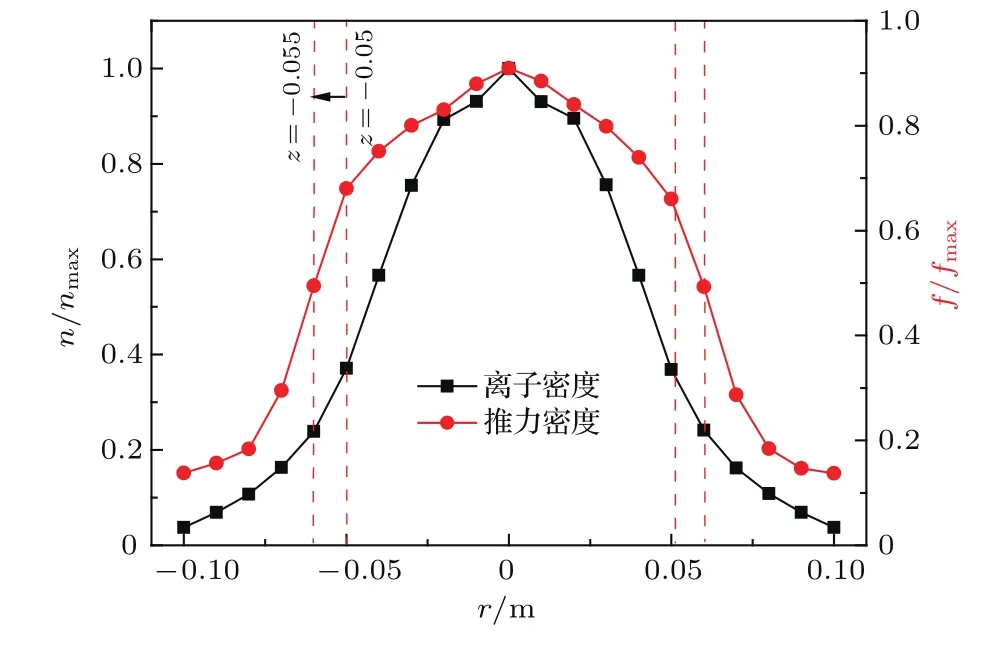
图9 推力密度分布与放电室出口离子密度分布比较Fig.9.Comparison between thrust density and ion density in discharge chamber.

进一步对比发现,相比放电室出口处的离子密度分布,推力密度快速下降对应的径向位置扩大了约5 mm,同时归一化推力密度在放电室边缘附近也略有上升,即推力密度沿径向分布更为均匀.这主要是由于栅极透过率特性导致的.放电室中心附近离子密度高,则流入栅孔的离子数量更多,基于栅孔电流越大其透过率越低的特性[20],通过减少喷出离子的数量而减小了栅孔束流产生的推力;在推力器边缘处离子密度较低,栅孔具有较高的透过率,相应提高了栅孔束流的推力.由此可见,栅极的透过率特性有助于提高推力密度的均匀性.

3.5 推力验证

为了验证数值计算的准确性,采用实验测试进行验证,同时结合经验公式通过计算进行对比分析.推力测试在兰州空间技术物理研究所TS-7实验平台上开展,采用微小推力法进行测试,推力测量精度为0.1 mN.

图10为数值计算、实验测试以及经验模型结果的对比.经验模型计算中,束流发散角因子β取0.98[22],双荷离子补偿系数α为0.97,氙离子质量为2.18×10−25kg.结果显示:随着屏栅电压增大,三种方法获得的推力具有相同的变化趋势,即随着屏栅电压升高,推力逐渐增大.进一步对比可知,采用经验模型计算下的推力值最大,实验测试结果次之,仿真计算结果最小.

图10 推力验证与对比Fig.10.Thrust veri fi cation and comparison.

分析认为,经验模型中束流离子喷出速度按均一化处理,即所有离子的速度增量均为(2eVb/mi)0.5,认为屏栅电压全用于离子加速,忽略了电荷交换碰撞效应所带来的能量损失等影响,使得经验模型中离子喷出速度偏大从而导致计算值偏大.仿真计算中较好地解决了该误差的存在,但同时也忽略了中性原子所产生的微推力,使得仿真计算结果略微偏低.在屏栅电压960—1040 V范围内,与实验测试结果相比,数值计算最大误差约2.8%,经验模型计算最大误差约4.1%.

4 结 论

采用PIC-MCC法对栅极束流引出进行了数值仿真,对束流多组分粒子喷出数量和速度等微观参数进行分析,同时得到了各组分粒子产生的推力贡献比特性.将数值计算、经验模型与实验测试结果进行对比验证,得到如下结论.

1)推力器的推力产生过程中,束流中的单价离子产生推力比例最高(约为84.63%),双荷离子次之(约13.55%),CEX离子最小(1.82%).双荷离子具有较高的喷出速度,在喷出数量一定的情况下,虽然可以提高推力性能,但是也对栅极造成的腐蚀将更加显著,从而减少推力器的寿命.因此,仍需对双荷离子比例进行适当控制.而CEX离子喷出速度和数量均相对较小,因此认为电荷交换碰撞对推力影响很小.

2)离子推力器的推力密度分布具有较好的中心轴对称性.推力密度在推力器中心处最大,沿着径向方向先快速减小后趋于稳定,在推力器边缘处推力密度最小,LIPS-200离子推力器的推力密度范围为0.01—0.19 mN/cm2.

3)离子推力器的推力密度分布相比放电室出口的离子密度分布具有更好的均匀性.当放电室中心附近离子密度较高时,流入栅孔离子数量越多(栅孔电流越大),由于栅极透过率随着栅孔电流增大而单调下降,使得喷出离子数量相应减少,从而降低了中心附近的推力.反之放电室边缘附近离子密度较低时,由于栅极透过率较高,相应增大了推力.

4)相比现有的经验模型,数值计算结果与实验测试数据有更好的一致性.采用数值仿真方法,通过跟踪粒子运动轨迹,大量统计出束流离子喷出数量和速度,可以更好地描述束流离子微观参数的差异性,因此,相比经验模型具有更好的准确度.

[1]Burak K K,Deborah A L 2017J.Propul.Power33 264

[2]Li J X,Wang Z H,Zhang Y B,Fu H M,Liu C R,Krishnaswamy S 2016J.Propul.Power32 948

[3]Zhang T P,Wang X Y,Jiang H C 2013Presented at the 33th International Electric Propulsion ConferenceWashington,USA,October 6–10,2013 p2013-48-1

[4]Zhou Z C,Gao J 2015Spacecraft Engineer.24 6(in Chinese)[周志成,高军 2015航天器工程 24 6]

[5]Williams L T,Walker M L R 2014J.Propul.Power30 645

[6]Yamamoto N,Tomita K,Yamasaki N,Tsuru T,Ezaki T,Kotani Y,Uchino K,Nakashima H 2010Plasma Sources Sci.T.19 045009

[7]Brophy J R,Wilbur P J 1985AIAA J.23 1731

[8]Takao Y,Miyamoto T,Yamawaki K,Maeyama T,Nakashima H 2002Vacuum65 361

[9]Goebel D M,Wirz R E,Katz I 2007J.Propul.Power23 1055

[10]Kitamura S,Miyazaki K,Hayakawa Y,Yoshida H,Akai K 2003Acta Astronaut52 20

[11]Hruby V,Martinez-Sanchez M,Bates S,Lorents D 199425th AIAA Plasmadynamics and Lasers ConferenceColorado,USA June 20–23,1994 p94-2466-1

[12]Bramanti C,Izzo D,Samaraee T,Walker R,Fearn D 2009Acta Astronaut64 735

[13]Walker R,Bramanti C 200642nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference&ExhibitCalifornia USA,July 9–12,2006 p2006-4669-1

[14]Sovey J S,Rawlin V K,Patterson M J 2001J.Propul.Power17 517

[15]Chen J J,Zhang T P,Jia Y H,Li X P 2012High Power Laser and Particle Beams24 2469(in Chinese)[陈娟娟,张天平,贾艳辉,李小平2012强激光与粒子束流24 2469]

[16]Yasutaka I,Toshiyuki O 2001Presented at the 27th International Electric Propulsion ConferencePasadena,USA,October 15–19,2001 p01-101-1

[17]Chen M L,Xia G Q,Mao G W 2014Acta Phys.Sin.63 182901(in Chinese)[陈茂林,夏广庆,毛根旺2014物理学报63 182901]

[18]Ren J X,Li J,Xie K 2013Plasma Sci.Technol.15 702[19]Li J,Chu Y C,Cao Y 2012J.Propul.Technol.33 131(in Chinese)[李娟,楚豫川,曹勇 2012推进技术33 131]

[20]Chen M L,Xia G Q,Xu Z J,Mao G W 2015Acta Phys.Sin64 094104(in Chinese)[陈茂林,夏广庆,徐宗琦,毛根旺2015物理学报64 094104]

[21]Zhou Z C,Wang M,Zhong X Q,Chen J J,Zhang T P 2015Chin.J.Vacuum Sci.Technol.35 1088(in Chinese)[周志成,王敏,仲小清,陈娟娟,张天平 2015真空科学与技术学报35 1088]

[22]Herman D A,Gallimore A D 2013Presented at the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,Joint Propulsion ConferencesFlorida USA,July 11–14,2013 pp2004–3958

[23]Zheng M F,Jiang H C 2011J.Propul.Technol.32 762(in Chinese)[郑茂繁,江豪成 2011推进技术 32 762]

[24]Jia Y H,Zhang T P,Zheng M F,Li X K 2012J.Propul.Technol.33 991(in Chinese)[贾艳辉,张天平,郑茂繁,李兴坤2012推进技术33 991]

[25]Zhang Z,Tang H B,Ren J X,Zhang Z,Wang J 2016Rev.Sci.Instrum.87 113502