具有次近邻相互作用的五量子比特XXZ海森伯自旋链的热纠缠∗

2018-03-18刘贵艳毛竹周斌

物理学报 2018年2期

刘贵艳毛竹周斌

(湖北大学物理与电子科学学院，武汉 430062)

1 引言

量子纠缠作为量子系统中的最基本特征之一,因其所特有的物理性质,在量子计算与量子信息领域中得到了广泛的应用,例如量子隐形传态[1]、量子超密编码[2]以及量子秘钥分发[3]等.在固态系统中实现与调控量子纠缠是人们关注的研究热点.海森伯自旋链作为一种简单的固态量子体系已成为人们研究量子纠缠的理想模型之一.众所周知,体系的量子效应会受到环境温度的重要影响,热涨落将抑制量子效应的产生.在量子纠缠态的制备中温度被看成是一个非常重要的调控参数,人们由此提出热纠缠的概念.Arnesen等[4]首次在海森伯模型中研究了热纠缠的性质,随后人们对各种两量子比特海森伯模型和多量子比特海森伯模型的热纠缠和配对纠缠特性开展了广泛的理论研究[5−14].研究表明,温度、磁场、自旋相互作用的各向异性和Dzyaloshinkii-Moriya(DM)相互作用等各种参数的变化都对体系热纠缠性质起到重要的调控作用.

在海森伯自旋链模型热纠缠的研究中,人们较多考虑的是最近邻量子比特自旋相互作用.实际上,一种J1-J2海森伯模型也引起了人们的研究兴趣,该模型中同时考虑了最近邻自旋相互作用和次近邻自旋相互作用[15,16].在J1-J2海森伯模型中,由于次近邻相互作用的引入导致阻挫效应,对体系的磁性有着重要的影响.研究发现,在一些准一维化合物中,如CuGeO3[17]和NaV2O5[18]等存在次近邻自旋相互作用.最近,有一些理论工作研究了具有次近邻相互作用的多量子比特海森伯模型中的纠缠性质[19−26].如Gu等[19]研究了温度和次近邻相互作用参数的变化对具有次近邻相互作用的一维海森伯自旋链中最近邻量子比特及次近邻量子比特配对纠缠的影响.他们数值计算了该自旋的体系中纠缠消失所对应的临界温度.Liu等[23]研究了具有次近邻相互作用的三量子比特XXX海森伯模型在非均匀磁场作用下的配对热纠缠性质. Şahintaş和Akyüz[26]研究了具有次近邻相互作用的四量子比特XXZ海森伯模型中的纠缠性质.他们重点讨论了DM相互作用和阻挫参数对最近邻量子比特及次近邻量子比特配对纠缠的影响.

本文研究具有次近邻相互作用的五量子比特XXZ海森伯模型中的热纠缠性质;利用数值计算方法分别计算最近邻量子比特和次近邻量子比特共生纠缠度;研究上述两种共生纠缠对随温度、磁场强度、DM相互作用、自旋相互作用及阻挫参数的变化关系;给出理论模型和纠缠度的计算方法,以及纠缠度的数值计算结果,并讨论各参数对纠缠度的影响.

2 理论模型和纠缠度

2.1 理论模型

研究的具有次近邻相互作用五量子比特XXZ海森伯自旋链模型如图1所示,系统哈密顿量H由下式给出:

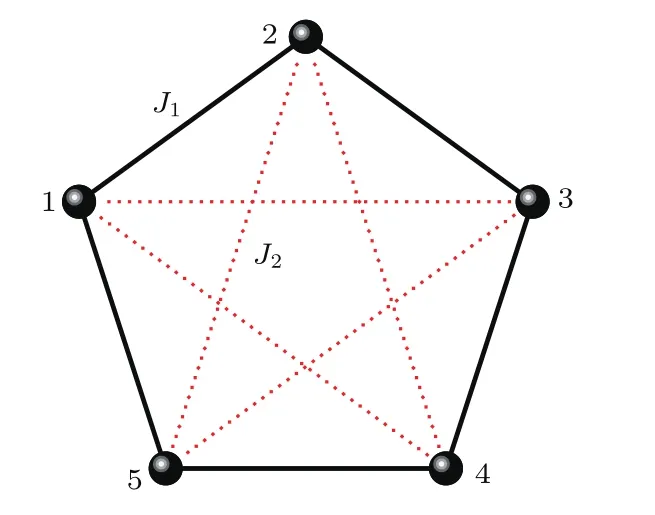
图1 五量子比特海森伯自旋链示意图黑色点代表自旋1/2的量子比特,黑色实线代表最近邻相互作用记为J1,红色虚线代表次近邻相互作用记为J2Fig.1.Five-qubit Heisenberg spin chain.The black dot represents a qubit with spin 1/2,the black lines represent the interaction between the nearest neighboring qubits named as J1,and the red dashed lines represent the interaction between the next nearest neighboring qubits named as J2.

2.2 纠缠度

哈密顿量(1)式的本征值和对应的本征矢分别为En和|ψn〉(n=1,2,···,32),在温度为T时,系统的密度矩阵为

其中Z为系统的配分函数

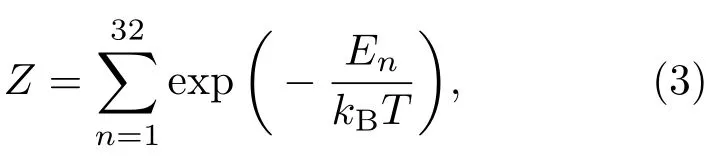
计算中取玻尔兹曼常数kB=1.

为了研究上述五量子比特海森伯自旋链的纠缠性质,计算第i个量子比特和第j个量子比特之间的共生纠缠度Cij,共生纠缠度的定义为[27−29]

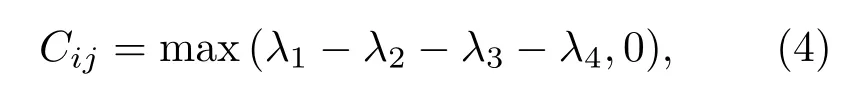
其中λn是算子Rij的本征值的平方根,Rij定义为

λn按降序排列,即λ1≥λ2≥λ3≥λ4;ρij是约化密度矩阵,是ρij的复共轭矩阵;纠缠度Cij的取值由0到1,Cij=0表示无纠缠,Cij=1表示系统处于最大纠缠态,0＜Cij＜1表示部分纠缠.根据图1中自旋链结构的对称性,下面分别讨论最近邻两量子比特的共生纠缠度C12与次近邻两量子比特共生纠缠度C13随参数的变化关系.

3 结果与讨论

基于共生纠缠度的定义,用数值计算方法研究具有次近邻相互作用五量子比特XXZ海森伯自旋链模型热纠缠性质,分别求解最近邻两量子比特共生纠缠度C12和次近邻两量子比特共生纠缠度C13在不同的温度、磁场强度、DM相互作用参数及各向异性参数下随阻挫参数的变化关系.

3.1 磁场与温度对C12和C13的影响

图2 在不同温度和磁场强度下,C12和C13随阻挫参数α变化情况 (a),(d)B=0;(b),(e)B=1;(c),(f)B=2;这里取D=0,Δ1=Δ2=1和J1=1Fig.2.C12and C13versus frustration parameter α for different temperature and magnetic fi eld:(a)and(d)B=0;(b)and(e)B=1;(c)and(f)B=2.Here,D=0,Δ1=Δ2=1 and J1=1.

首先考虑DM相互作用为零(D=0)的情形.当各向异性参数Δ1=Δ2=1时,即系统由各向异性的XXZ自旋模型转变为各向同性的XXX自旋模型,在不同磁场和温度下,C12和C13随阻挫参数的变化关系由图2给出.从图2(a)中可以发现,在没有磁场作用下(B=0),温度较低时(如T=0.3)C12在阻挫参数−3.3＜α＜1.0区间出现一个非零的平台(C12=0.25).这表明,阻挫参数绝对值的增大将压制最近邻两量子比特纠缠的产生.随着温度的升高,出现纠缠(C12不为零)的阻挫参数区间逐渐缩小,而且伴随着C12最大值的减小.如当温度分别为T=0.7和T=1时,出现纠缠的阻挫参数区间分别为(−2.7,0.9)和(−2.3,0.7),相应的C12最大值为0.21和0.15.图2(b)和图2(c)显示,在同样的温度下,出现纠缠的阻挫参数区间随着磁场强度的增加而缩小.以温度T=0.7为例,磁场强度分别为B=1和B=2时,出现纠缠的阻挫参数区间分别为(−2.0,0.9)和(−1.4,0.9).图2(d)—(f)给出了次近邻两量子比特共生纠缠度C13随阻挫参数的变化关系.显然,C13表现出与C12完全不同的变化关系.次近邻两量子比特共生纠缠度C13不为零出现在阻挫参数α＞1,而α＜1时次近邻两量子比特配对纠缠消失.以T=0.3为例,当磁场为零时(如图2(d)所示),当α＞1,随α的增加,C13迅速达到最大值0.25并保持不变.当磁场强度增加时,如B=2,C13的最大值提高到0.35,同样对于α＞1,C13随α的增加迅速饱和并保持不变.这表明,对于反铁磁情形(J1,J2＞0)而言,当次近邻相互作用参数大于最近邻相互作用参数时,有利于次近邻两量子比特配对纠缠的产生,而最近邻两量子比特纠缠消失.

为了更进一步讨论磁场对C12和C13的影响,取温度T=0.3为例,计算了随磁场和阻挫参数变化的共生纠缠度,结果由图3给出(图3中蓝色区域代表纠缠度为零,红色最深的区域对应纠缠度为0.35).从图3(a)中可以看出,随着磁场增大,一方面出现最近邻量子比特纠缠的区域逐渐缩小,另一方面共生纠缠度C12先增大后逐渐减小直至消失.同时发现,当磁场超过一定强度（B＞2.5）时,出现纠缠的区域被限制在一个很窄的参数空间内(见图3(a)中浅蓝色区域),而且共生纠缠度C12也被压制在0.1以内.图3(b)对应共生纠缠度C13的变化情况.在磁场小于3时,出现次近邻量子比特纠缠的区域大致保持不变,而磁场超过3时,产生纠缠的临界阻挫参数随磁场增大逐渐增大.在图3(b)中,随着磁场和阻挫参数的变化,存在使得共生纠缠度达到饱和值C13=0.35的一个较大参数区域.

当考虑自旋相互作用各向异性时(取Δ1=Δ2=0.5),C12和C13随阻挫参数变化关系由图4给出.比较图2和图4发现,自旋相互作用各向异性对上述两种共生纠缠度都有显著的影响.以T=0.3为例,当磁场为零时,C12不为零的阻挫参数区有两个(见图4(a)),即分别是−2.5＜α＜0.9和α＜−3.6,第一个参数区的范围相对于各向同性时(Δ1=Δ2=1,见图2(a))略有缩小;而第二个参数区是各向同性时所没有的.随着磁场的增加,存在纠缠的第一个阻挫参数区相应的C12的值减小,即最近邻两量子比特纠缠受到磁场的抑制;对于第二个参数区而言,磁场反而有利于最近邻两量子比特纠缠的产生(见图4(b)和(c)).同样,随着阻挫参数的变化,次近邻两量子比特纠缠不为零的参数区也有两个,分别是1＜α和α＜−2.7(当T=0.3和B=0时,见图4(d)),其中第一个参数区类似于各向同性的情形(见图2(d)),而在第二参数区则是由自旋相互作用各向异性诱导出次近邻两量子比特间的配对纠缠.对于其他一定的温度和磁场强度,也存在着对应C13不为零的与上述情形相似的阻挫参数区(见图4(e)和(f)).如,当T=1和B=1时,对应于1.2＜α和α＜−3.3,存在次近邻两量子比特配对纠缠(即C13/=0).

在自旋相互作用各向异性的情形下,同样取温度T=0.3为例,图5给出了共生纠缠度C12和C13随磁场和阻挫参数变化的等高图.与图3(a)比较,不难发现,在自旋相互作用各向异性的情形下,图5(a)显示共生纠缠度C12在阻挫参数较大的负值区间出现新的纠缠区.在这个新的纠缠区,随磁场增大,C12先逐渐增大至最大值,后被抑制直至消失.同样,对于C13而言(如图5(b)所示),与图3(b)比较,考虑到自旋相互作用各向异性,在阻挫参数较大的负值区间也出现了新的纠缠区.特别是当阻挫参数取较大的负值时,如α=−8,C13随磁场增大出现了两个极大值.

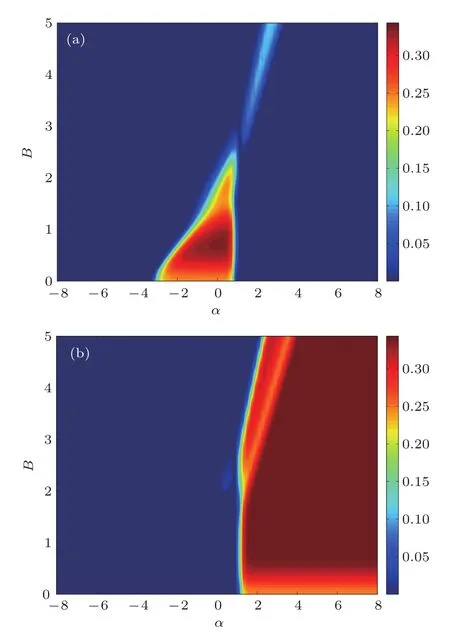
图3 共生纠缠度随阻挫参数α及磁场强度变化情况 (a)C12;(b)C13;这里取T=0.3,D=0,Δ1=Δ2=1和J1=1Fig.3. Concurrence versus frustration parameter α and magnetic fi eld:(a)C12;(b)C13.Here,T=0.3,D=0,Δ1=Δ2=1 and J1=1.

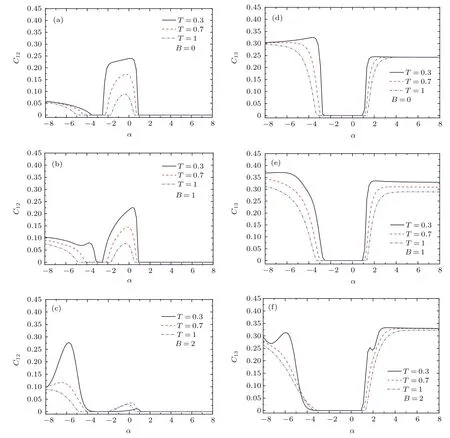
图4 在不同温度和磁场强度下,C12和C13随阻挫参数α变化情况 (a),(d)B=0;(b),(e)B=1;(c),(f)B=2;这里取D=0,Δ1=Δ2=0.5和J1=1Fig.4.C12and C13versus frustration parameter α for different temperature and magnetic fi eld:(a)and(d)B=0;(b)and(e)B=1;(c)and(f)B=2.Here,D=0,Δ1=Δ2=0.5 and J1=1.

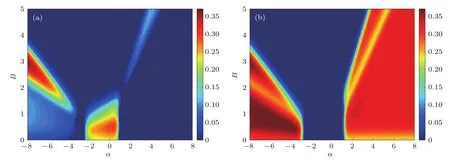
图5 共生纠缠度随阻挫参数α及磁场强度变化情况 (a)C12;(b)C13;这里取T=0.3,D=0,Δ1=Δ2=0.5和J1=1Fig.5.Concurrence versus frustration parameter α and magnetic fi eld:(a)C12;(b)C13.Here,T=0.3,D=0,Δ1=Δ2=0.5 and J1=1.

3.2 DM相互作用对C12和C13的影响

下面研究DM相互作用对共生纠缠度的影响.在各向异性参数Δ1=Δ2=0.5的情形下,图6和图7给出了对应于不同温度、磁场强度及DM相互作用参数,最近邻两量子比特共生纠缠度C12和次近邻两量子比特共生纠缠度C13随阻挫参数的变化情况.

图6(a)—(c)给出了没有外加磁场(B=0)时C12随阻挫参数变化情况.显然,在一定的阻挫参数区域，DM相互作用有利于最近邻两量子比特配对纠缠的产生.以T=0.7为例,当不考虑DM相互作用时(D=0,见图4(a)),最近邻两量子比特共生纠缠度C12不为零的阻挫参数区有两个,即分别是−2.2＜α＜0.8和α＜−4.2;当考虑DM相互作用时(见图6(a)—(c)),随DM 相互作用参数的增大,C12最大值增大,如D=0.5,1,2相对应的C12最大值分别是0.28,0.32,0.33.而且,C12不为零的第一个阻挫参数区的范围变大,如D=0.5,1,2相对应的C12不为零的第一个阻挫参数区的范围分别是−2.6＜α＜1,−3.3＜α＜2.9和−4.1＜α＜6.1;同时也注意到随DM相互作用参数的增大,C12不为零的第二个阻挫参数区向左偏移.图6(d)—(i)给出了有外加磁场时C12随阻挫参数变化情况.显然,在有外加磁场时,DM相互作用对最近邻两量子比特配对纠缠的影响与无磁场时定性一致.

图6 在不同温度、磁场强度和DM相互作用参数下,C12随阻挫参数α变化情况,Δ1=Δ2=0.5和J1=1 (a)B=0,D=0.5;(b)B=0,D=1;(c)B=0,D=2;(d)B=1,D=0.5;(e)B=1,D=1;(f)B=1,D=2;(g)B=2,D=0.5;(h)B=2,D=1;(i)B=2,D=2Fig.6.C12versus frustration parameter α for different temperature,magnetic fi eld and DM interaction parameter,Δ1= Δ2=0.5 and J1=1:(a)B=0,D=0.5;(b)B=0,D=1;(c)B=0,D=2;(d)B=1,D=0.5;(e)B=1,D=1;(f)B=1,D=2;(g)B=2,D=0.5;(h)B=2,D=1;(i)B=2,D=2.

图7 在不同温度、磁场强度和DM相互作用参数下,C13随阻挫参数α变化情况,Δ1=Δ2=0.5和J1=1 (a)B=0,D=0.5;(b)B=0,D=1;(c)B=0,D=2;(d)B=1,D=0.5;(e)B=1,D=1;(f)B=1,D=2;(g)B=2,D=0.5;(h)B=2,D=1;(i)B=2,D=2Fig.7.C13versus frustration parameter α for different temperature,magnetic fi eld and DM interaction parameter, Δ1=Δ2=0.5 and J1=1:(a)B=0,D=0.5;(b)B=0,D=1;(c)B=0,D=2;(d)B=1,D=0.5;(e)B=1,D=1;(f)B=1,D=2;(g)B=2,D=0.5;(h)B=2,D=1;(i)B=2,D=2.

图7(a)—(c)给出了没有外加磁场(B=0)时C13随阻挫参数的变化情况.不难发现,随着DM相互作用的增强,相应次近邻两量子比特共生纠缠度C13为零的阻挫参数区域增大.以T=0.7为例,对应于D=0.5,1和2时,C13为零的阻挫参数区域分别是(−3.1,1.1),(−3.4,1.1)和(−4.2,1.0). 而且在α＞1区域,随着DM相互作用的增强,温度对C13的影响受到抑制.当考虑磁场的作用时,在一定的磁场范围内,如B=1时(见图7(d)—(f)),DM相互作用对次近邻两量子比特配对纠缠的影响与无磁场时也是定性一致的.当磁场适当增加时,如B=2时(见图7(g)—(i)),DM相互作用的增强使得原先C13为零的阻挫参数区在温度较低时(如T=0.3)也产生了次近邻两量子比特配对纠缠.

4 结论

基于数值计算方法求解共生纠缠度,研究了具有次近邻相互作用的五量子比特XXZ海森伯自旋模型热纠缠性质.分别讨论了最近邻两量子比特和次近邻两量子比特共生纠缠度随系统各种调控参数的变化规律.研究结果表明,阻挫参数的变化对上述两种共生纠缠度的影响表现出不同的性质.例如,对于反铁磁情形而言,当次近邻相互作用参数大于最近邻相互作用参数时,有利于次近邻两量子比特配对纠缠的产生,而最近邻两量子比特的纠缠消失.同时发现,温度、磁场、DM 相互作用以及各向异性参数对配对纠缠有着不同程度的影响.因此,通过选择适当的模型参数,可以有效地调节和提高五量子比特XXZ海森伯自旋链的共生纠缠度.

[1]Bennett C H,Brassard C,Crépeau C,Jozsa R,Peres A,Wootters W K 1993Phys.Rev.Lett.70 1895

[2]Bennett C H,Wiesner S J 1992Phys.Rev.Lett.69 2881

[3]Ekert A K 1991Phys.Rev.Lett.67 661

[4]Arnesen M C,Bose S,Vedral V 2001Phys.Rev.Lett.87 017901

[5]Wang X G 2001Phys.Rev.A64 012313

[6]Wang X G 2001Phys.Lett.A281 101

[7]Zhang Y L,Zhou B 2011Acta Phys.Sin.60 120301(in Chinese)[张英丽,周斌 2011物理学报60 120301]

[8]Cao M,Zhu S Q 2005Phys.Rev.A71 034311

[9]Wang X G,Fu H C,Solomon A I 2001J.Phys.A34 11307

[10]Hou J M,Du L,Ding J Y,Zhang W X 2010Chin.Phys.B19 110313

[11]Wang Y H,Xia Y J 2009Acta Phys.Sin.58 7479(in Chinese)[王彦辉,夏云杰 2009物理学报 58 7479]

[12]Hu Z N,Yi K S,Park K S 2007J.Phys.A:Math.Theor.40 7283