改进频率调谐显著算法在疵点辨识中的应用

王传桐， 胡 峰， 徐启永， 吴雨川， 余联庆

(武汉纺织大学 机械工程与自动化学院, 湖北 武汉 430074)

中国是面料生产大国，提高面料疵点检测准确率对提升纺织品质量和竞争力具有重要意义[1]。Gabor滤波簇具有多尺度、多方向滤波能力，可有效地克服疵点图像对比度低的影响，提高疵点检测准确率[2-3]；但是，Gabor滤波簇存在滤波器数量多、运算量大的问题，使疵点检测耗时较长[4]。

频率调谐显著算法(FT)[5-6]从频域角度出发，对真彩图像进行高斯低通滤波，然后将图像转换到Lab空间，针对每个颜色通道计算单个像素与整幅图像的平均色差，将3个通道的平均色差平方和作为该像素的显著值，具有抗噪能力强，计算量小的优点[5]；但是将FT算法应用到疵点辨识中，其辨识精度受高斯滤波器模板尺寸影响大；高斯滤波图像中存在椒盐噪声；检测单一颜色纺织品(如坯布、镜面面料)疵点时，对亮度和颜色差异较小的疵点识别困难[7]。相较于FT算法中使用的Lab空间，HSV颜色空间更适合单一颜色纺织品疵点检测，但是，其色调特征H与饱和度特征S及亮度特征V的取值范围不同且变化不一致，所得到的显著值不能很好地体现出各个分量。针对这些问题，本文对FT算法进行了改进，并应用到了单一颜色纺织品疵点检测中。

1 FT算法原理及缺陷

FT算法的基本计算步骤[5]为：首先，采用高斯滤波器对图像进行滤波，滤波器模板尺寸凭人工经验选取；然后，滤波后的图像由RGB颜色空间转化成Lab颜色空间；最后，根据式(1)计算图像I在像素点(i,j)处的显著值：

S(i,j)=‖Iμ-Iωhc(i,j)‖

(1)

式中：Iμ为图像在 Lab空间的像素算术平均值；Iωhc是高斯滤波后的图像；‖•‖为l2范数。

FT算法应用到纺织品疵点识别中，存在如下问题：1) 高斯滤波器模板尺度对疵点辨识精度影响大。主要原因是：取值较小时，高斯滤波器的平滑窗口较小，许多细小背景纹理轮廓不能被平滑，降低了疵点纹理特征的灵敏度；取值较大时，滤波后疵点轮廓变得模糊，加大辨识难度。采用不同模板尺度r进行高斯滤波后的疵点图像如图1所示。可见：模板尺度为3时的滤波图，面料纹路被完整保留；模板尺寸为6时的滤波图，面料纹理被弱化的同时，疵点轮廓信息也被完整保留；模板尺度为12时的滤波图，面料纹理和疵点轮廓同时被平滑；2) 对单一颜色纺织品疵点进行检测时，基于Lab颜色空间的特征向量Iu对亮度和颜色差异较小的疵点灵敏度不高。Lab空间中的L代表光亮度，其值从0(黑色)至100(白色)，b和a代表色度坐标，其中a代表红-绿轴，b代表黄-蓝轴。Lab的优点在于L分量密切匹配人类亮度感知，可通过修改a、b分量的输出色阶进行精确的颜色平衡，或通过L分量调整亮度对比。对单一颜色纺织品进行疵点检测时，多数疵点颜色和纺织品自身颜色基本一致，不一致的位置体现在疵点区域与正常区域亮度不同，因此，Lab空间中只有L通道对疵点敏感；3) 从图1(c)、(d)中可发现，背景区存在深/暗不一的噪声点，呈椒盐分布状，在后续显著过程中会凸显出来；4) 在一幅图像中，各个特征通道中特征分量的取值范围不一致，且快慢也不同。很多情况下，3个特征的显著值不在同一个数量级上，导致计算所得到的显著值S(i,j)仅能突出某个特征，忽略了其他特征[6]。

图1 高斯低通滤波效果图Fig.1 Picture after Gaussian blurring. (a) Original picture; (b) r=3; (c) r=6; (d) r=12

2 改进FT疵点检测方法

2.1 改进的FT算法

1) 针对高斯滤波器模板尺度对疵点辨识精度影响大的问题，本文提出采用离散粒子群算法[8-9]和Ncut准则[10-11]对高斯滤波模板取值进行优化，基本思路如图2所示。首先，设置训练样本集，用初始模板尺寸进行高斯滤波；然后，将滤波图像由RGB颜色空间转换到HSV颜色空间；接下来，使用自适应中值滤波器在不同通道进行二次滤波；其次，计算各通道特征与整幅图像均值之间的距离，并进行归一化；最后，显著化处理及提取显著化后图像的特征向量，估计特征向量的Ncut准则值，其值越大说明模板尺寸越好。使用粒子群算法的目的是利用其优化速度快的优势，尽快在搜索空间找到合适的模板尺寸。Ncut准则原来主要用于衡量类可分性的优劣，现在将其作为粒子群算法的适应度函数，目的在于在其他条件不变的情况下，衡量高斯模板尺度是否提高了疵点特征向量的灵敏度。文献[10]中阐述了Ncut准则的基本原理。改进FT算法的主要目的是增强疵点区域与背景的对比度，提高疵点特征向量的灵敏度，达到高效准确辨识疵点目的。

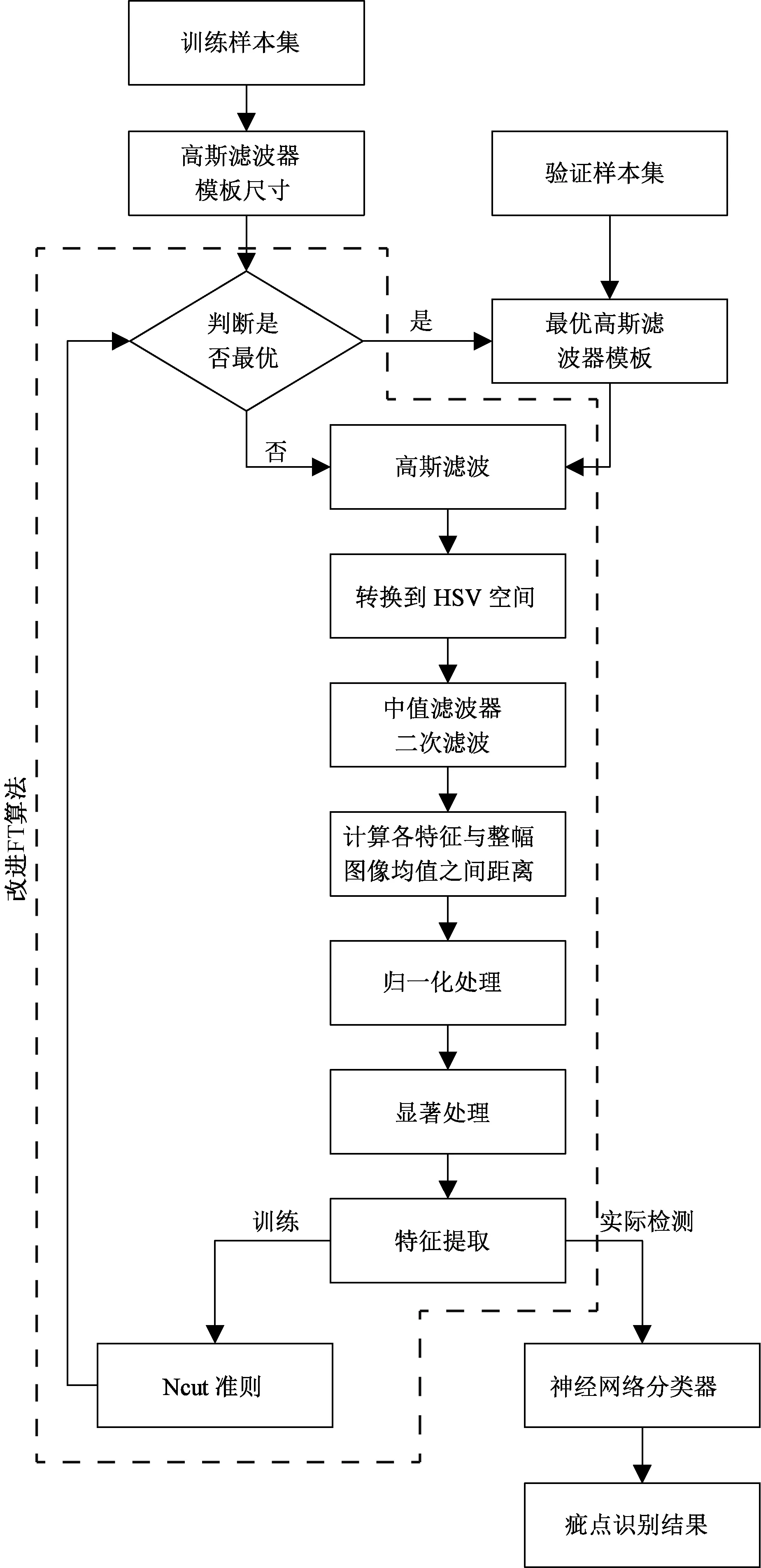
图2 基于改进FT算法的疵点检测Fig.2 Detection of fabric defects based on modified FT algorithm

2) 针对检测单一背景颜色的纺织品疵点时，Lab颜色空间中式(1)特征向量Iu对亮度差异较小的疵点灵敏度不高的问题，推荐采用HSV空间代替Lab空间。HSV空间中H通道表征色调，用来表示颜色的类别；S通道表征饱和度，用来表示颜色的鲜艳程度；V通道表征亮度。通常情况下，疵点区域和正常区域相比，亮度、颜色或者饱和度都会存在差异。HSV颜色空间能更直观地表达色彩的明暗、色调和鲜艳程度，在FT算法中对存在细小颜色和亮度差异的疵点具有更好的显著效果，因此，HSV空间中S通道与V通道均可有效区分疵点与正常纹理。

3) 针对高斯滤波后疵点图像存在椒盐噪声的问题，本文使用自适应中值滤波器在S通道和V通道对图像IG进行二次滤波，减少噪声点对后续显著计算的影响。

4) 针对频率调谐显著过程中遇到的色调特征H与饱和度特征S及亮度特征V的取值范围不一致(H∈[0,360]，S,V∈[0,100])等问题，对3个特征分量的显著值进行归一化。具体过程如下。

针对二次滤波图像Im，计算色调特征H、饱和度特征S和明度特征V所对应的整幅图像的均值uH、uS和uV；在各特征通道中，分别计算每个像素点与整幅图像均值之间的距离，如式(2)～(4)所示。

SH(i,j)=[H(i,j)-uH]

(2)

SS(i,j)=[S(i,j)-uS]

(3)

SV(i,j)=[V(i,j)-uV]

(4)

式中：SH、SS、SV分别为在HSV空间中各特征通道下像素点与均值间的距离；H(i,j)、S(i,j)、V(i,j)分别为H通道、S通道、V通道中像素点(i,j)

归一化处理,得：

(5)

(6)

(7)

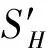
对每个像素进行特征融合，得到最终显著性值。

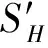
(8)

式中ωH、ωS、ωV分别为3个空间所对应的权值，本文选取ωH=ωS=ωV=1/3。

2.2 疵点检测算法

基于改进FT算法的疵点检测算法步骤为：1)初始化离散粒子群参数；2) 图像做高斯滤波处理，得到新图像IG；3) 将图像IG转换到HSV颜色空间，使用自适应中值滤波器对图像IG进行二次滤波，得到滤波图像Im；4)计算各通道下二次滤波图像像素点与整幅图像均值之间的距离；5) 归一化距离并融合特征，得到每个像素的最终显著值；6)将显著图作为输入向量，Ncut准则函数作为适应度函数；7) 计算每个粒子适应度值；8) 检测是否达到终止条件。如果达到则停止，否则返回步骤2；9) 对图像显著图进行特征提取，本文提取灰度共生矩阵中4个方向的对比度、能量、相关度、熵组成1×16维的特征向量；10) 使用训练样本特征向量对概率神经网络进行训练，对验证样本疵点图像分类。

3 结果与分析

本文实验选取2类平纹组织织物进行，分别为F1和F2数据库。F1数据库：纬密为264根/(10 cm)，经密为340根/(10 cm)，纱线线密度为18.23 tex；采集分辨率为0.089 mm/像素。F2数据库：纬密为375根/(10 cm)，经密为410根/(10 cm)，纱线线密度为36.34 tex；采集分辨率为0.089 mm/像素。F1和F2数据库中包含线头、缺经、破洞、油污、竹节等疵点类型以及正常面料图像，疵点灰度图尺寸为100像素×100像素。分别从子数据库中选取100张图片作为训练样本集，每类图片数量为20张；100张图片作为验证样本集，每类图片数量为20张。

3.1 疵点图像采集方法

采集疵点图像时，光源和相机分别置于面料两侧，与面料垂直，利用正常区域和疵点区域透光性的不同，提高棉粒、竹节、粗纬、断经等疵点区域与正常区域的亮度对比度。这可以通过图3示出的不同采集方式下的疵点图像给予证实：如图3(a)、(c)拍摄时，光源和相机置于面料同一侧，2种不同纹理面料的经疵对比度极低，肉眼很难分辨；如图3(b)、(d)拍摄时，光源和相机分别置于面料两侧，发现疵点位置与正常区域对比度明显增强。由此说明，利用面料疵点区域和正常区域透光性的不同，可在亮度和饱和度上提高疵点对比度，为改进的FT算法更好发挥功能提供支持。

图3 不同采集方式下的疵点图像Fig.3 Fabric defect images with different acquiring modes. (a) Coarse pick of reflection; (b) Coarse pick of transmission;(c) Missed warp of reflection; (d)Missed warp of transmission

3.2 显著方法对比实验

在相同情况下，对比研究本文改进的FT算法、原始FT方法以及进行高斯模板尺寸优化但没有进行二次滤波和使用HSV空间的FT方法，验证本文推荐改进FT算法的合理性和有效性。

以F1、F2数据库中面料疵点显著处理对比为例，部分结果如图4、5所示。

由图4可看出：使用原始FT算法对纺织品疵点图像进行显著时，面料本身纹路细节全部保留，对油污和线头类疵点进行显著时，疵点位置已经几乎不能识别；使用高斯滤波器尺寸进行优化后的FT算法对纺织品疵点图像进行显著时，对于竹节、破洞和线头疵点均可达到良好的显著效果，但对于油污类疵点进行显著处理时，油污位置和面料纹路被显著的亮点混杂，显著效果较差，使用本文改进的FT算法对竹节、油污、破洞和线头类疵点进行显著时，均可实现良好的显著效果。

由图5可看出：使用原始FT算法对预处理后的图像进行显著时，面料本身纹路细节全部保留，对油污类疵点进行显著时,疵点位置显著不明显；使用高斯滤波器尺寸进行优化后的FT算法对纺织品疵点图像进行显著时，对各类疵点均能实现良好的显著效果；使用本文改进的FT算法对疵点进行显著处理时，对各类疵点显著效果良好，并且油污类疵点的背景纹理明显弱化。

通过图4、5中对正常面料图像进行显著的结果可发现，在没有疵点的情况下，使用改进的FT算法对面料进行显著，面料纹路被显著成为不规则状的小亮点。比较纺织品疵点图像和正常图像的显著图可发现，正常面料与存在疵点的面料显著图存在很大的纹理差异，因此，本文提取面料显著图的纹理信息作为特征值，可达到疵点辨识的目的。

造成这种现象原因是：1) 基于离散粒子群算法和Ncut准则的高斯滤波模板优化算法，可实现高斯滤波模板尺寸的最优化，达到最佳显著效果；2) 与Lab空间相比，HSV空间更适合对纺织品疵点图像进行显著处理；3) 中值滤波可有效地消除高斯滤波后图像中存在的椒盐噪声；4) 对3个特征分量的显著值进行归一化，可有效地解决不同特征分量下取值范围不一致的问题。

3.3 疵点辨识对比实验

在相同条件下，将如下3种算法进行对比实验研究，验证本文推荐疵点检测方法的合理性和有效性。

1) 本文推荐的基于改进的FT算法与灰度共生矩阵相结合的疵点检测方法(IFT算法)。

2) 基于FT算法与灰度共生矩阵相结合的疵点检测方法(FT算法)。该方法采用FT算法对纺织品疵点图像进行显著处理，提取灰度共生矩阵特征并进行分类，其步骤和方法1相同。

注：A—原始图像；B—原始FT算法；C—使用高斯滤波器尺寸优化后的FT算法；D—改进FT算法。图4 F1数据库频域协调显著效果图Fig.4 Saliency image of datebase F1 using different methods.(a) Slab yarn; (b) Oil stain; (c)Hole; (d) Thrum; (e)Normal fabric

注：A—原始图像;B—原始FT算法;C—使用高斯滤波器尺寸进行优化后的FT算法;D—改进FT法。图5 F2数据库频域协调显著效果图Fig.5 Saliency image of datebase F2 using different methods.(a) Cracked ends; (b) Oil stain; (c)Hole; (d) Missing end; (e)Normal fabric

分别从子数据库中选取150张样本，每类疵点图片数量为30张。其中：每类疵点图像中选取10张图片作为训练样本集；20张图片作为验证样本集。利用式(9)计算疵点分类准确率。

(9)

式中：R为准确识别率；Pr为准确识别疵点图片张数；PA为识别疵点图片总数。

对F1、F2数据库中面料疵点使用IFT算法和G-Isomap算法、FT算法进行疵点辨识对比，统计结果如表1、2所示。其中，各疵点类型下数据表示准确识别图片张数。

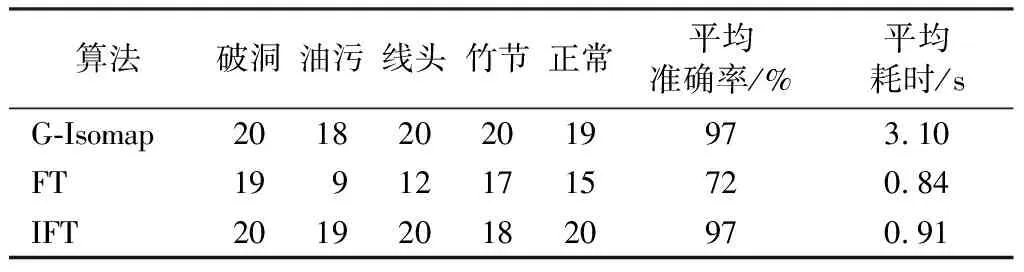
表1 数据库F1辨识统计结果Tab.1 Statistical results of database F1

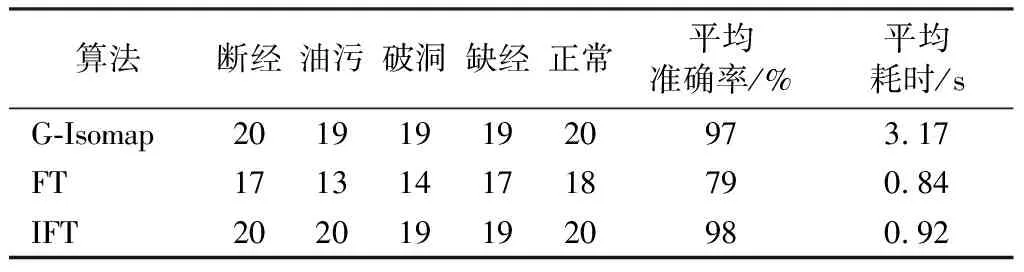
表2 数据库F2辨识统计结果Tab.2 Statistical results of database F2

通过表1、2统计结果可知：在使用G-Isomap方法对破洞、线头以及缺经类疵点进行检测时，均可准确识别，对于油污类疵点和正常面料进行检测时，存在少量误检；FT方法在对破洞类疵点和缺经疵点检测时，检测效果良好，但是，对其他类疵点和正常面料进行检测时，误检率过高，准确率均低于75%；IFT方法对破洞、线头疵点面料和正常面料进行检测时，均实现准确识别，对于缺经和油污面料进行检测时，存在少量误检，但准确率均在90%以上。通过平均准确率结果可知：FT算法准确率最低，IFT算法识别准确率与Gabor算法相同且均达到较好的检测效果；但是，IFT算法的运算速度比Gabor算法提升了约70%。

通过表2还可观察到：在使用G-Isomap算法辨识疵点时，破洞类疵点和正常面料均可实现准确识别，缺经、粗经和竹节类疵点检测准确率均为95%；FT方法在对破洞类疵点、缺经疵点和正常面料检测时，检测效果稍好，但是检测准确率均在90%以下，对其他类疵点进行检测时，检测准确率均低于75%；IFT方法对破洞、缺经类疵点和正常面料进行检测时，均可准确检测，对粗经和竹节类疵点进行检测时，检测准确率均为95%。通过平均准确率可发现：IFT算法识别准确率率高于Gabor算法，FT算法检测平均准确率极低；同时，IFT算法的运算速度明显高于Gabor算法。

通过表1、2可发现，使用改进的频率调谐显著算法对疵点图像进行疵点显著处理，可降低面料纹理对识别精度的影响，在保障面料分类精度的同时提高了辨识速度。

4 结 论

使用改进频率调谐显著算法对真彩图像进行疵点显著处理，可克服面料纹理对疵点辨识精度的制约，保障面料分类精度的同时提高了辨识速度。基于Ncut和离散粒子群算法的模板参数优化模型能找出频域协调显著模型中高斯滤波器的最优模板尺寸，增强了疵点显著效果，提高了疵点辨识的效率和精度。

[1] 管声启，石秀华. 基于频域滤波的织物疵点检测[J]. 计算机应用，2008， 28(10)： 2673-2675.

GUAN Shengqi，SHI Xiuhua. Fabric defects detection based on frequency domain filtering[J]. Journal of Computer Application，2008， 28(10)：2673-2675.

[2] 屈博, 卢朝阳, 李静, 等. 一种改进的多通道Gabor滤波器面料瑕疵检测方法[J].纺织学报, 2009, 30(12):37-40.

QU Bo, LU Zhaoyang, LI Jing, et al. An improved multichannel Gabor filter algorithm for fabric defect detection[J]. Journal of Textile Research, 2009, 30(12):37-40.

[3] 王传桐, 胡峰, 徐启永, 等. 采用Gabor滤波簇和等距映射算法的织物疵点检测方法[J]. 纺织学报, 2017, 38(3):162-167

WANG Chuantong, HU Feng, XU Qiyong, et al. Detection of fabric defects based on Gabor filters and Isomap[J]. Journal of Textile Research, 2017, 38(3):162-167.

[4] 林如意. 基于图像处理技术的纺织品瑕疵检测方法[D]. 杭州：杭州电子科技大学，2013：11-14.

LIN Ruyi. Fabric defect detection based on image processing technology[D]. Hangzhou: Hangzhou Dianzi Universiy, 2013：11-14.

[5] ACHANTA R, HEMAMI S, ESTRADA F, et al. Frequency-turned salient region detection [C]// Proceedings of 2009 IEEE Computer Society Conference on Computer Society Conference on Computer Vision and Pattern Recognition Workshop. Miami: IEEE Computer Society, 2009:1597-1604.

[6] 于乃昭，姚志均，杨波. 一种改进的频率调谐显著性检测方法[J]. 舰船电子对抗, 2013, 36(1):57-61.

YU Naizhao, YAO Zhijun, YANG Bo. An improved Frequency tuned-based saliency detection method [J]. Shipboard Electronic Countermeasure, 2013, 36(1):57-61.

[7] 刘洲峰, 赵全军, 李春雷, 等. 基于局部统计与整体显著性的织物疵点检测算法[J]. 纺织学报, 2014, 35(11):62-67.

LIU Zhoufeng, ZHAO Quanjun, LI Chunlei, et al. Fabric defect detection algorithm using local statistic features and global saliency analysis[J]. Journal of Textile Research, 2014,35(11):62-67.

[8] LIU Yan, GU Xueping. Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization [J]. IEEE Transactions on Power Systems, 2007, 22(3):1267-1274.

[9] ALBERTO García-Villoria, RAFAEL Pastor. Introducing dynamic diversity into a discrete particle swarm optimization [J]. Computer and Operation Research, 2009, 36(3):951-966.

[10] 胡峰, 苏讯, 刘伟, 等. 基于改进局部线性嵌入算法的故障特征提取方法[J]. 振动与冲击，2015, 34(15):201-204.

HU Feng, SU Xun, LIU Wei, et al. Fault feature Extraction based on improved locally linear embedding[J]. Journal of Vibration and Shock, 2015, 34(15):201-204.

[11] 胡峰, 王传桐, 吴雨川, 等. 基于改进监督LLE算法的故障特征提取方法[J]. 振动与冲击，2015(21):119-123.

HU Feng, WANG Chuantong, WU Yuchuan, et al. Fault features extraction based on improved supervised locally linear embedding [J]. Journal of Vibration and Shock, 2015(21):119-123.