基于神经网络的卷染机控制系统设计

魏苗苗， 刘洲峰

(中原工学院 电子信息学院， 河南 郑州 450007)

布卷张力的变化和卷轴速度的波动会引起染色不匀，影响卷染机染色质量。因此，在卷染过程中，保证布卷张力和卷轴速度恒定是卷染机控制系统设计中一项十分重要的工作[1-2]。传统的卷染机多采用双直流电机进行控制，但是其对布卷张力和卷轴速度的控制难以达到预期效果[3-6]，此外，在高温高压环境下，机器的腐蚀速率会加快，因此传统的依靠传感器进行布卷张力和卷轴速度调节的控制系统已经不适用[7]。

本文采用交流变频调速传动系统，并辅以智能控制算法，进行卷染机控制系统设计。该控制系统可以有效控制高温高压环境下卷染机的染色过程。

1 传统PID控制算法

目前，基于PID算法的自动控制系统因其结构简单、控制方便而在大多数工业生产中得到广泛的应用，该类控制算法包括比例、积分与微分3类控制分量[8-11]。PID控制器是将预先设定值与实际输出值的差值的比例、积分和微分的线性组合作为综合控制量对被控对象进行控制，算法的具体原理如图1所示。

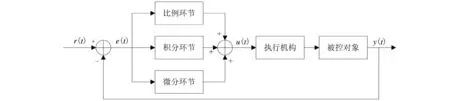
图1 PID算法原理图[9]

在PID控制系统的使用过程中，PID控制算法的参数确定是难点。在实际应用中，这些参数会受具体工作环境的影响，使得传统 PID控制器存在参数粗糙、适应性差和控制效果欠佳等问题，难以适应复杂的工况。针对这一问题，本文采用基于逆向反馈(Back Propagation, BP)神经网络[12]的PID控制算法来实现对高温高压下卷染机张力和速度的控制。

2 基于BP神经网络的PID控制器

针对PID控制算法存在的问题，本文利用BP神经网络对PID算法的参数进行自适应确定。算法的核心思想是，利用BP神经网络的多次反馈迭代过程，通过神经网络良好的特征提取能力对PID控制参数(比例KP、积分KI和微分参数KD)进行调整以逼近最优的控制效果。控制器结构如图 2所示。

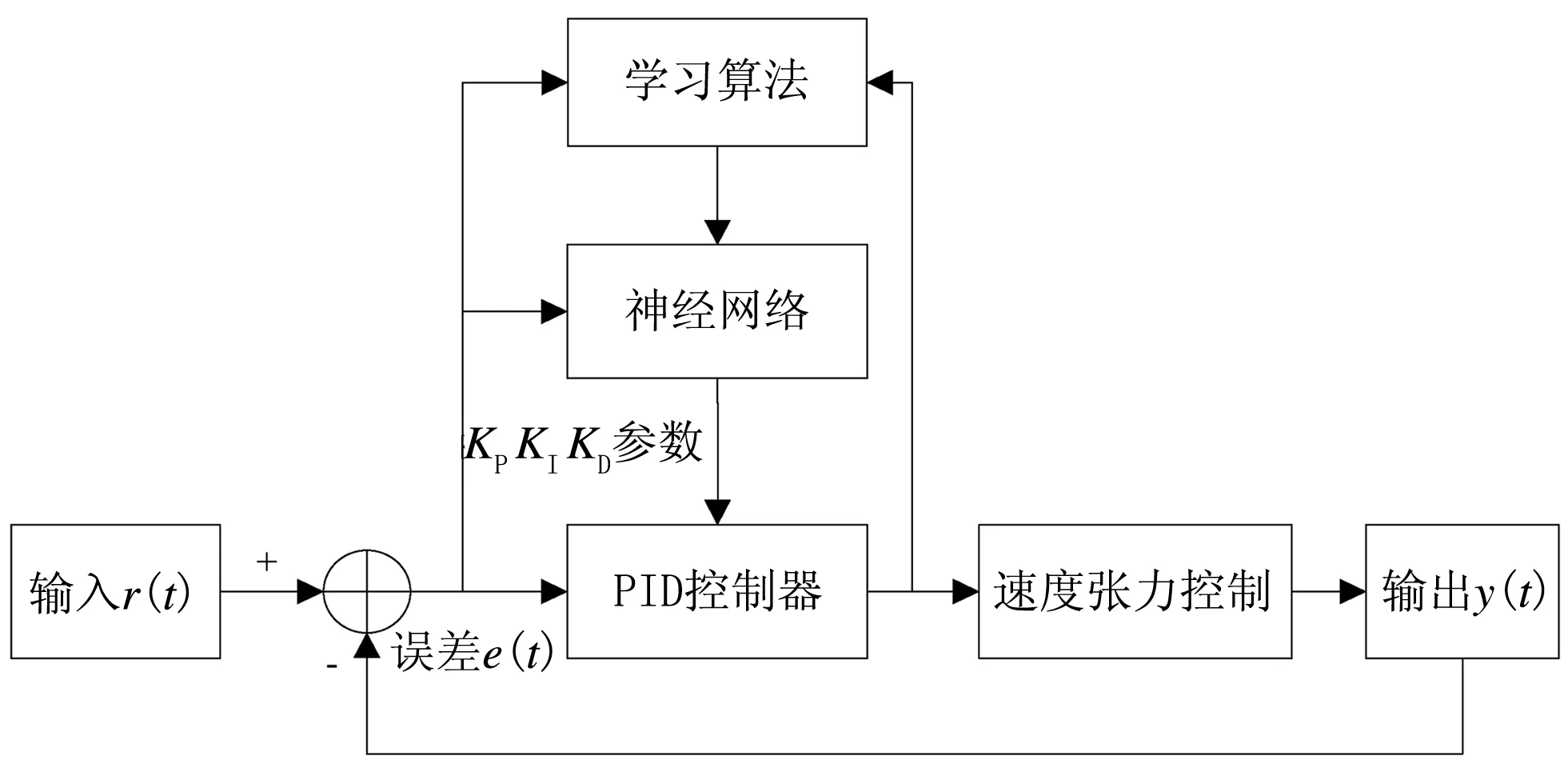
图2 基于逆向反馈神经网络的PID控制器结构图[13]

本控制系统仍然采用以PID算法为核心的交流变频控制器对速度和张力进行控制，但对 PID 的3个参数(比例 、积分和微分)的调整却是利用逆向反馈神经网络来实现的。利用神经网络的迭代学习能力对控制算法的参数进行更为精准和细化的调整，以期逼近最优控制参数组合。三层结构逆向反馈神经网络的结构图如图3所示。

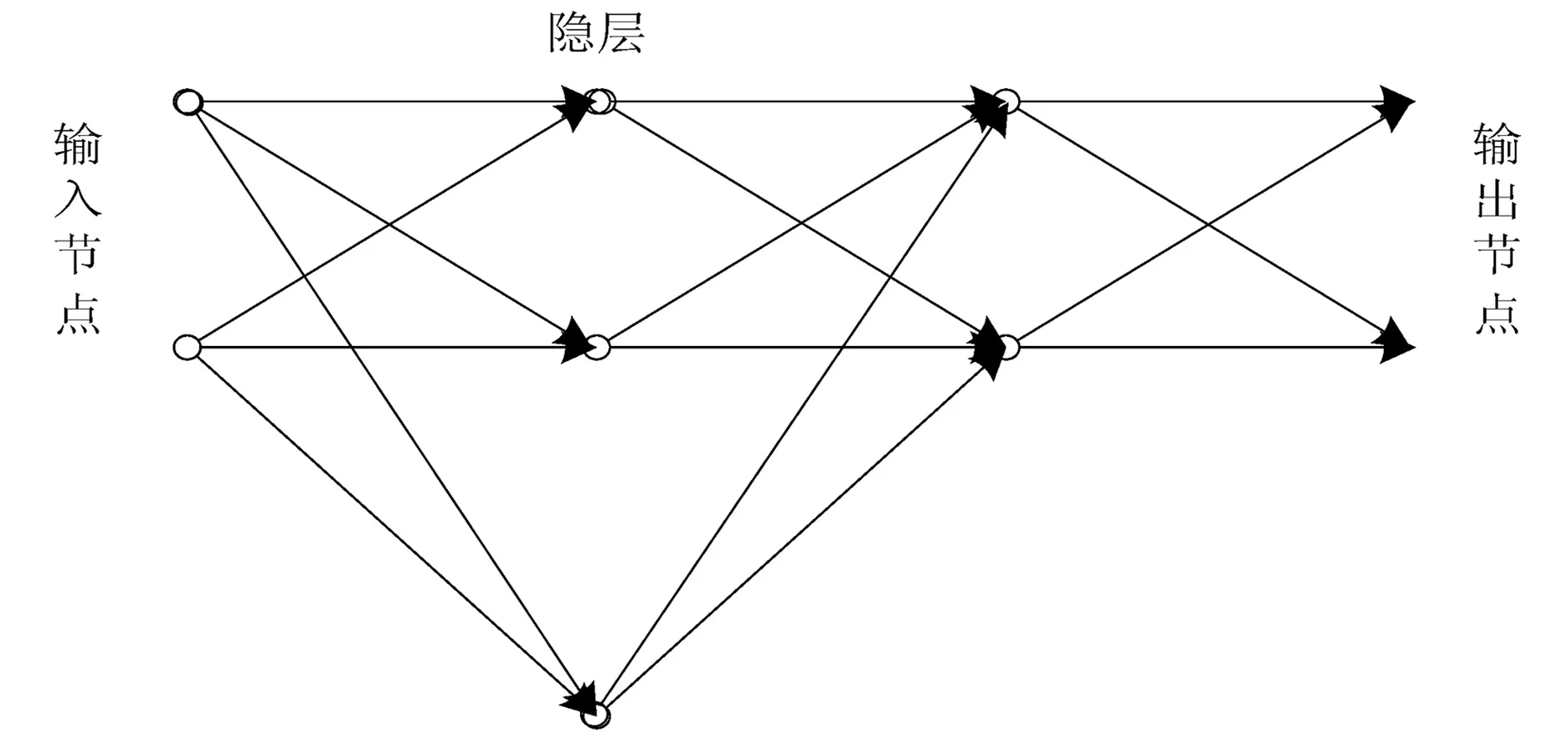
图3 三层神经网络结构图

图3中，隐层的输入由输入层的输入和偏置信息之和构成。将相邻两层之间的权值作为对输入序列进行加权的权向量，对应公式为：

(1)

式(1)中，i表示输入层神经元编号(最大值为M)，代表隐层神经元；x表示各层输入序列；w表示相邻两层间的权向量；上标表示对应层，上标(1)表示输入层，上标(2)表示隐层。设隐层神经元的激活函数为：

(2)

那么隐层的输出应为：

(3)

这样最终输出层的输入为：

(4)

其中Q为隐层神经元的个数；上标(3)表示输出层。

设输出层神经元的激活函数为：

(5)

这样输出层的输出为：

(6)

则输出层所有输出为：

(7)

输出层3个输出分别对应PID算法的比例参数(KP)、积分参数(KI)和微分参数(KD)。 本系统的性能指标函数选取为：

(8)

根据BP神经网络学习算法对各层权值进行调整。 输出层将计算出的性能指标误差传递到隐层权值的公式为：

(9)

式(9)中，η表示神经网络学习速率；α表示控制系统惯性系数。由基于逆向反馈神经网络的PID算法方程可以推得：

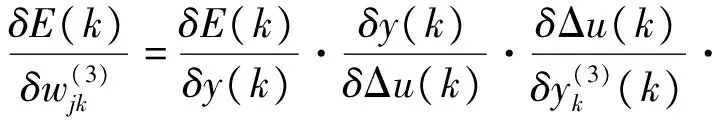
(10)

同时可知：

(11)

这样就可以获得：

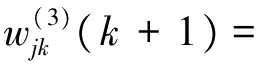
(12)

其中：

(13)

继续分析，可以得到隐层加权系数的调整迭代公式为：

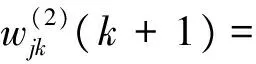
(14)

(15)

算法的具体实现步骤为：

(1)根据控制系统设计要求，设置逆向反馈神经网络的层数M、每层神经元个数Q以及神经网络的学习速率η和系统的惯性系数α。

(3)计算控制偏差e(k)=r(k)-y(k)，其中r(k)、y(k)分别为r(t)和y(t)的时刻采样值。

(4)计算逆向反馈神经网络各层的输入和输出值。

(5)根据输出层的3个输出值(KP、KI和KD)和偏差e(k)计算控制输出u(k)=u(k-1)+KP[e(k)-e(k-1)]+KIe(k)+KD[e(k)-2e(k-1)+e(k-2)]。

(7)更新输出值KP、KI和KD。

3 测试结果

测试内容包括两个方面：一是张力变化情况，二是卷速变化情况。图4为卷染机工作过程张力变化曲线图。

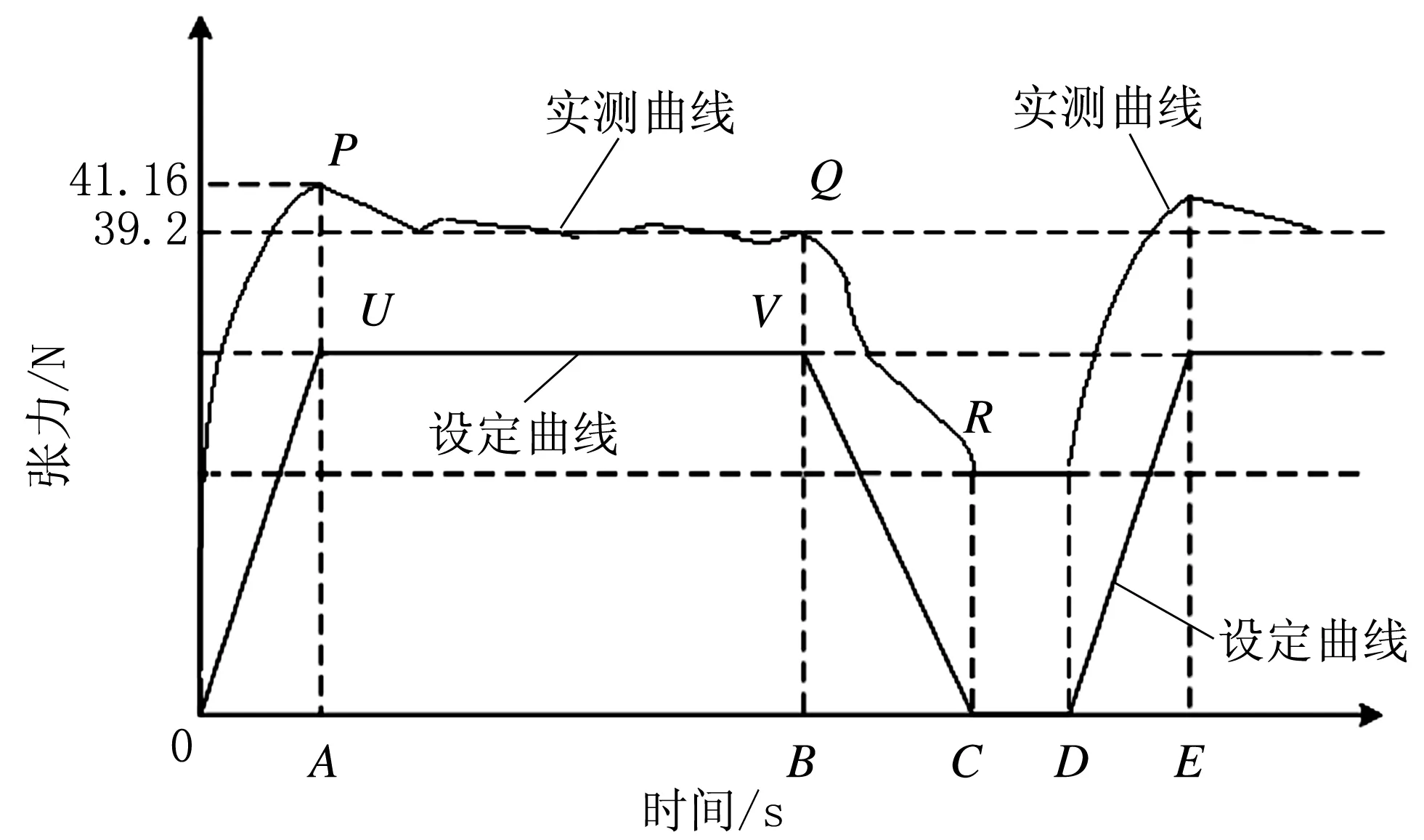
图4 卷染机工作过程张力变化曲线

从图4可以看出，张力变化过程包括4个阶段：加速阶段、摆动阶段、减速阶段和停止阶段。其中OA段为加速阶段，时长设为8 s；张力变化范围为19.6～39.2 N；超调量为5%；卷轴速度为0～100 m/min；加速阶段所用布长为6.6 m；在6.6 m布长上的张力变化为5%。摆动阶段是指OC整段，由加速OA、匀速AB和减速BC 3个阶段组成。此外，CD段为停止段，DE段为加速段。由于卷染过程中匀速运行是主要运行状态，因此本文主要考察匀速运行过程中实际测得的张力和速度数据。

本文在放卷一侧进行张力检测，在收卷一侧进行速度检测。由于放卷侧初始卷径在测量时未受卷轴张力的影响，因此卷径不发生变化，从而不会对卷轴卷染速度产生影响。而收卷侧因受张力影响而使布的厚度发生变化，从而使卷径变小，所以会影响卷轴卷染速度，一般情况下，在进行恒速度恒张力设计时会通过设置补偿系数来削弱这一影响。表1列出了匀速运行情况下卷染机的张力和速度的设定和实测结果，根据表1可得出张力控制误差在0.7%以内，速度控制误差在0.6%以内。由此可见，虽然补偿后仍然有误差，但是误差较小可以达到用户的使用要求。

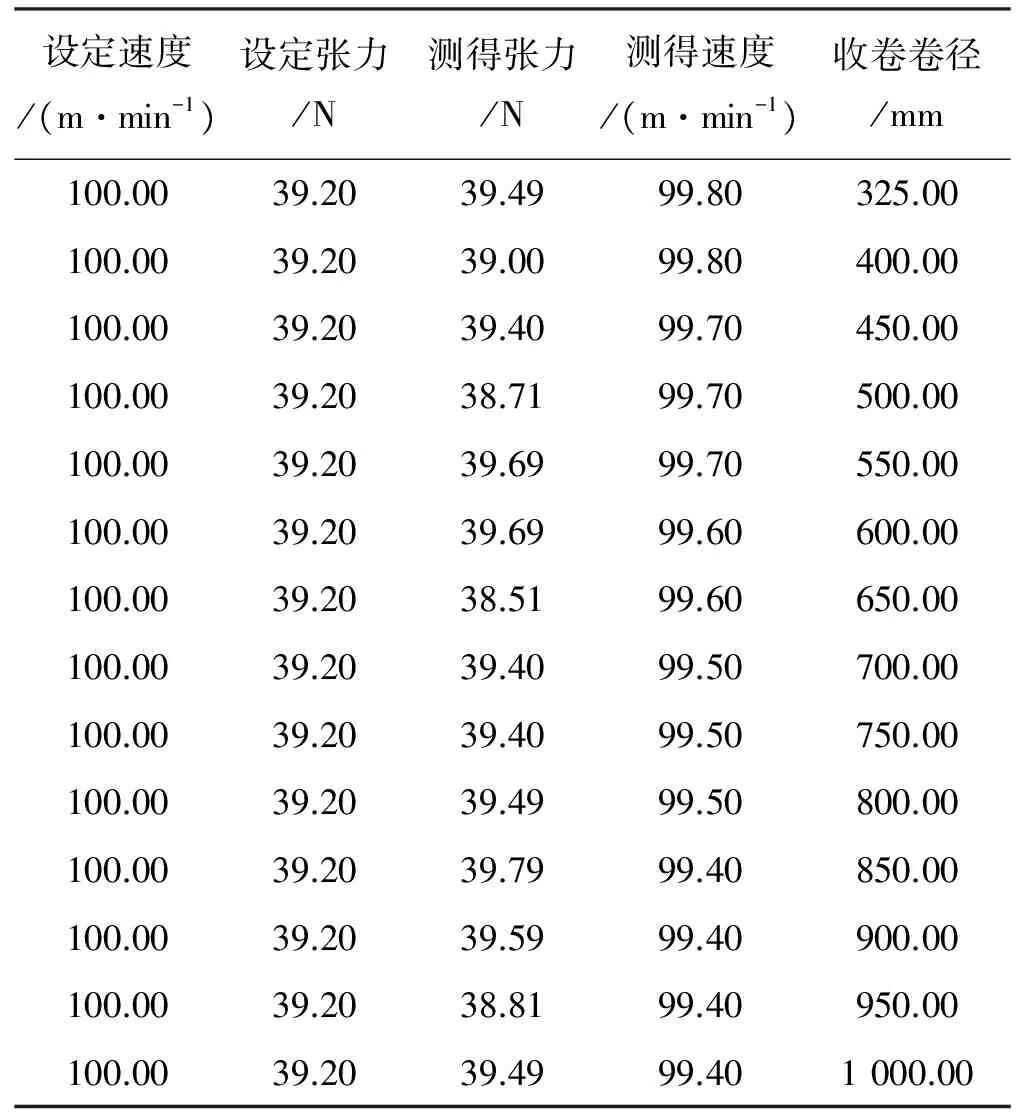
表1 设定和测试数据

4 结 语

张力和速度控制是影响织物染色质量的关键。本文选择基于BP神经网络的改进PID控制算法，对PID参数进行自适应调整。通过实际测试结果可知，在卷染过程中，改进的控制系统可以有效地实现恒速恒张力控制。

[1] 刘秉亮.卷染机恒线速度控制系统设计[D].济南：山东大学,2005.

[2] 文贝.双变频卷染机控制系统的设计[D].杭州：浙江理工大学,2016.

[3] 梁逸敏,陈栋,壮炳良.卷染机智能化控制系统设计与应用[J].轻纺工业与技术,2016,45(04):5-7.

[4] 盛卫锋,王小伟.卷染机中央控制系统[J].电子设计工程,2015,23(05):97-100.

[5] 梁逸敏,陈栋,壮炳良.ZHGR1800S型双变频自动卷染机控制系统[J].山东纺织经济,2016(07):39-40,35.

[6] 陈璐露.基于TMS320F2812的纺织印染中心卷绕功能自适应同步控制的研究[D].武汉：武汉纺织大学,2016.

[7] 江明,王龙明,陈跃东.基于PLC的交流变频调速控制高温高压卷染机研制[J].机电工程,2003(02):27-30.

[8] 杨骁.基于自适应PID算法的轧染机恒张力控制系统研究[D].辽宁：辽宁工业大学, 2014.

[9] 刘迪,李岩,张大为.一种改进型自适应PID控制算法的仿真与研究[J].仪表技术,2014(03):50-51,54.

[10] 何军红,尹旭佳,史常胜.PID控制算法在西门子PLC中编程及55实现[J].工业仪表与自动化装置,2012(05):79-82.

[11] 郭昌,高清维,崔桂梅.模糊PID控制算法在变频调速中的新应用[J].电机与控制应用,2011,38(08):19-22.

[12] 刘迪.基于神经网络的PID控制算法[D].哈尔滨：黑龙江大学,2008.

[13] Kang W N, Chu T, Zhao H X. The Design of Constant Tension System Basedon BP Neural Network PID Control[J]. Scientific Journal of Control Engineering,2014,4(2)：58-63.