基于改进响应面法的蒙华铁路良山边坡可靠度分析

2018-03-15李孝峰

中原工学院学报 2018年1期

李孝峰

(中铁十九局集团第六工程有限公司, 江苏无锡 214028)

随着我国“一带一路”倡议推进，更多的边坡及其他公路工程开始建设，这些基础设施的安全成为关键问题。边坡岩土体均质性差，多存在节理和断层等不良破碎体，采用单一固定值力学参数计算边坡岩土体安全可靠度显然不太合理。近年来，以可靠度指标为输出结果的岩土体稳定性可靠度分析方法被广泛认可，比如随机响应面法(SRSM)、一阶二矩法(FOSM)和蒙特卡洛法(Monte Carlo Simulation)[1-3]等。同时，为节省现场测试，子集模拟、随机有限元等数值模拟方法也被广泛用于对地下工程的可靠性分析[4-5]。这些方法主要依赖于计算机，具有样本量大、耗费时间长等特点。

响应面法在边坡结构可靠度计算中应用非常普遍，苏永华等将Sarma 法和传统响应面法相结合, 基于响应面法取样本点，用Sarma法来计算安全系数，提供了一种高效岩质边坡可靠性分析思路[6]；傅方煜等提出了边坡稳定二阶可靠度响应面的实用算法，其关键是在响应面法失效点的基础上把点代入二阶矩法来计算边坡可靠度，该方法可为边坡加固的可靠度分析提供有效指导[7]；张光耀等基于空间滤波法对传统响应面法进行改进,克服了传统响应面法不能有效解决局部解交接的问题[8]；李静萍等针对实际工程边坡存在多个滑裂面的问题提出了系统可靠度概念，采用多重响应面法来计算边坡所有可能的失效滑移面，计算结果更贴近边坡防治的工程实际[9]。总之，响应面法的样本点布置较多，而且存在局部解不收敛甚至失真等问题，找寻更好的方法并获取全局解很有必要。人工神经网络是基于逻辑符号的人工智能，可获取最优的近似响应面函数，能够克服传统方法非结构化信息方面的缺陷，具有自适应和自学习的特点[10-11]。因此，采用人工神经网络构造近似的响应面函数，可以从理论上有效地解决传统方法容易导致局部解的缺点，获得更为精确的全局解。

本文选取边坡岩土体的黏聚力c、内摩擦角φ和容重ρ为计算参数，并以均值和标准差进行表征。首先采用人工神经网络构造近似响应面函数，对边坡岩土体进行可靠度分析；然后以响应值为边坡安全系数，采用Janbu法进行分析计算；最后采用Matlab优化工具箱计算边坡岩土体的失效概率。

1 响应面法与人工神经网络组合

响应面法起源于试验设计(DOE)，由国外学者John B L和Joseph H G提出[2],假设一个因变量y受到n个因素影响，而每个因素有m个水平值，则需进行的试验总次数为mn。随着因素水平值增加或者因素个数增加，试验次数将呈几何数增长。因此，为研究出更优化的组合试验设计，同时又能得到准确结果，响应面法应运而生。

响应面法的核心内容在于样本点设计和回归系数获取。样本点设计，即因素点水平取值组合，它主要由轴点、均值点和角点组成(见图1)。角点一般根据析因设计来布置，假设因素为2个，则根据排列组合原理，存在4个组合；假设因素为3个，则根据排列组合原理，存在8个组合；以此类推，在包含n个因素的情况下，有2n组试验设计。对于均值点，一般进行一次试验，所有的样本点均取平均值进行计算。对于轴点试验，一个因素取最大值和最小值，剩余因素全部取均值，因而n个因素的情况下，有2n组试验设计。因此，试验总次数为2n+2n+1次。

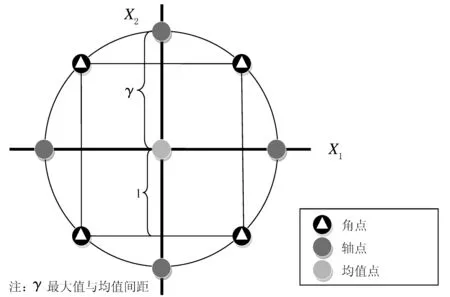
图1 以响应面法设计的样本点布置

构建近似函数时，函数一般为二次多项式，由自变量(即因素x1,x2,…,xn)与因变量y(即安全系数)组成，即：

(1)

式中：a为常数项回归系数；bj，bjj分别为一次项和二次项回归系数。

显然，式(1)含有的未知数个数为n(n+1)/2，试验次数必须多于未知数个数才能得到解析解。

样本点组合可直接采用Minitab软件得到。表1所示为三因素响应面复合设计。

回归系数借助于人工神经网络获得，具体操作如下：

(1)在设定初始参数γ和r(γ为初始权系数，r为临界值)的同时，假设边坡稳定性影响因素为m个，每个因素对应的评价水平为n个，则：

(i=1,2, …,m;j=1,2, …,n)

(2)

(2) 将已知样本从输入层输入所建立的BP人工

表1 三因素响应面复合设计表

神经网络中；

(3) 不断调整权系数，直到在输出层获取每个需评价指标的权系数(见图2)。

图2 从BP人工神经网络获取权系数示意图

2 用优化工具箱求解失效概率

假设边坡的安全系数为F，边坡极限状态安全系数Fmin=1，则边坡的功能函数为G(x)=F-Fmin。当功能函数等于0时，边坡的失效概率为：

Pf=P[G(x)<0]≈Φ(β)

(3)

式中：β为可靠度指标。

一旦计算出边坡可靠度指标β，就可判断边坡稳定性期望功能水平(见表2)。

表2 目标可靠度评价表

图3所示为极限状态函数及可靠度指标。可靠度指标和失效概率其实是正态分布的另一种表达方式。可靠度指标需满足下式：

(4)

式中：μj，σj分别为随机参数xi的均值和标准差；Y为岩土参数矩阵；C为参数间相关矩阵。对于式(4)，可以借助Matlab的优化工具箱进行求解。可靠度指标确定后，即可求得目标系统的失效概率。

图3 极限状态函数及可靠度指标示意图

边坡失效概率求解的基本思路如下：①确定影响边坡安全的自变量，即黏聚力c、内摩擦角φ和容重ρ；

②采用Minitab完成DOE，得到编码变量表；③根据编码变量对自变量黏聚力c、内摩擦角φ和容重ρ进行转换；④通过理论分析获取响应值，即边坡安全系数；⑤根据人工神经网络得到回归方程，与极限状态函数建立联系从而得到功能函数；⑥将相关系数矩车代入Matlab优化工具箱,最终获得目标的失效概率。

3 工程案例分析

3.1 工程概况

良山边坡位于蒙西到华中煤运铁路蒙华铁路江西段，边坡在江西省新余市渝水区良山镇境内(见图4)。该边坡为阶梯型边坡，相对高差为9.8 m，坡角为60°，上部相对高差为4.3 m，下部相对高差为5.5 m。边坡覆盖泥质碎石土，植被较发育，为典型土质边坡。坡址区属亚热带，四季分明，春季干旱多风，夏季炎热多雨，秋季气候凉爽，冬季寒冷少雪，年均降雨量为540～600 mm。

图4 良山边坡图像

3.2 可靠度分析

良山边坡岩土体力学参数选取容重、黏聚力和内摩擦角(见表3)。这3个参数的取值和变异系数根据勘察资料、原位及室内试验确定。确定3个参数的均值和标准差后，就可以按照表1来转换编码。根据文献[6]，一般取xmax=μ+ 1.645σ，xmin=μ- 1.645σ。二者对应编码分别为+1.645和-1.645。

表3 良山边坡力学参数

边坡安全系数(即响应值)可采用Janbu法进行计算。良山边坡计算模型如图5所示。

根据表1中15个试验组合，采用理正软件对边坡安全系数F进行计算，获取每个组合对应的安全系数值(见表4)。

根据表4，采用上述BP人工神经网络可获得良山边坡的回归系数。其回归函数为：

g(x)=1.800 7+1.108c+0.010 62φ-0.034 05γ

(5)

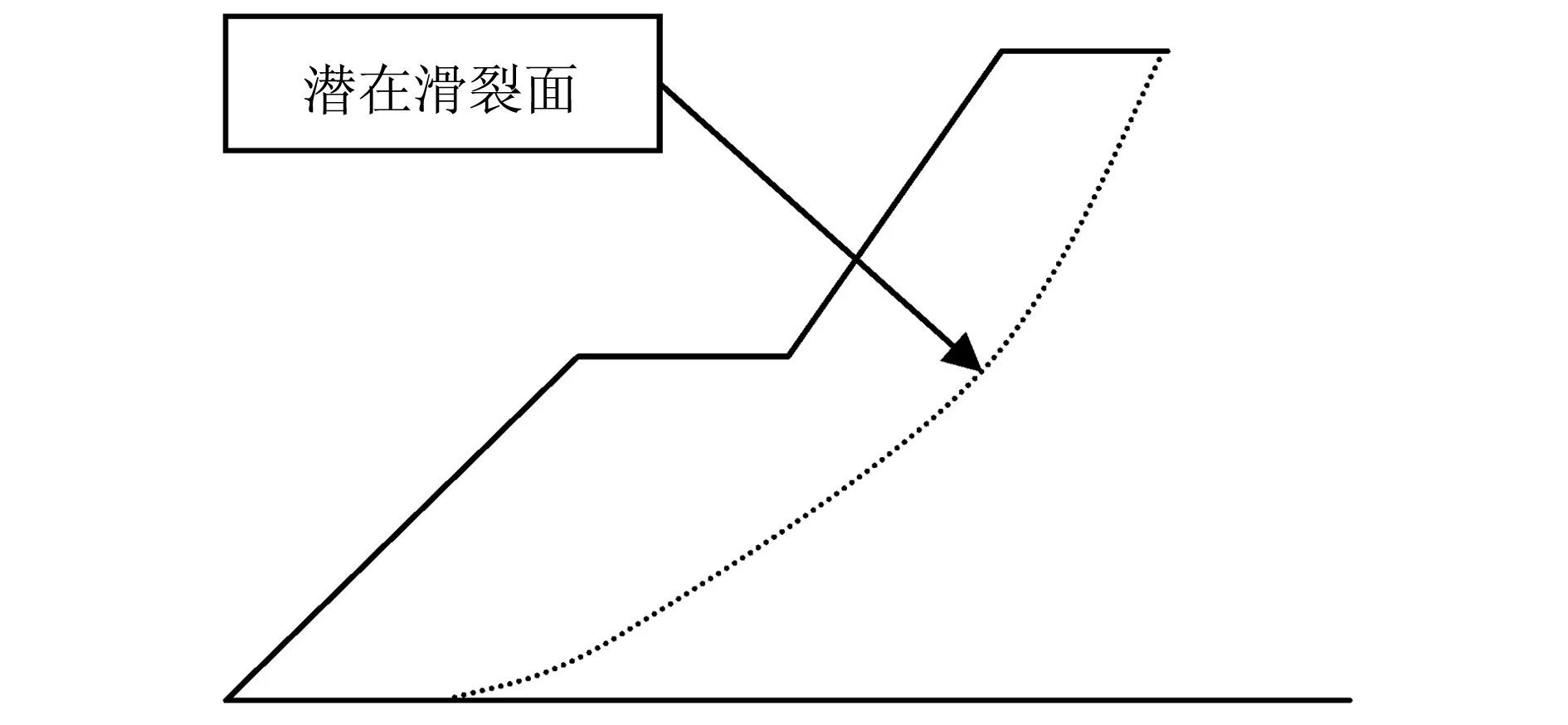
图5 良山边坡计算模型表4 良山边坡响应面设计

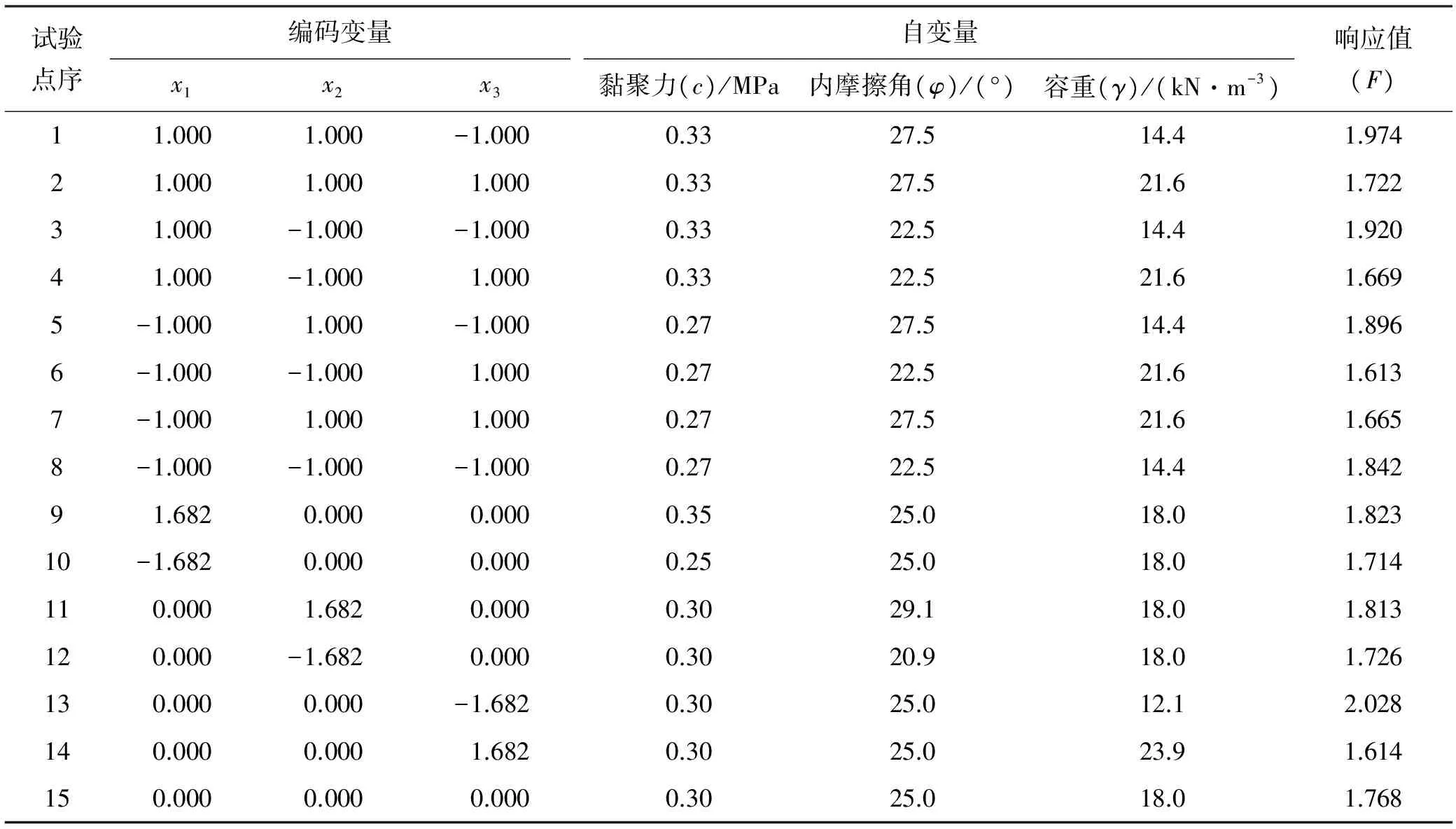
试验点序编码变量x1x2x3自变量黏聚力(c)/MPa内摩擦角(φ)/(°)容重(γ)/(kN·m-3)响应值(F)11．0001．000-1．0000．3327．514．41．97421．0001．0001．0000．3327．521．61．72231．000-1．000-1．0000．3322．514．41．92041．000-1．0001．0000．3322．521．61．6695-1．0001．000-1．0000．2727．514．41．8966-1．000-1．0001．0000．2722．521．61．6137-1．0001．0001．0000．2727．521．61．6658-1．000-1．000-1．0000．2722．514．41．84291．6820．0000．0000．3525．018．01．82310-1．6820．0000．0000．2525．018．01．714110．0001．6820．0000．3029．118．01．813120．000-1．6820．0000．3020．918．01．726130．0000．000-1．6820．3025．012．12．028140．0000．0001．6820．3025．023．91．614150．0000．0000．0000．3025．018．01．768

根据边坡工程设计规范，边坡极限状态安全系数Fmin=1，有功能函数：

G(x)=g(x)-1

(6)

采用Matlab优化工具箱可算得，边坡的失效概率为0.253%，对应的可靠度指标为3.4。其整个计算过程耗时约20 min。采用蒙特卡罗法计算的样本点数量为1012，计算时间约为2 h，边坡的失效概率为0.257%，对应的可靠度指标为3.4。良山边坡的“期望功能水平”为“较好”。