串联机械臂的仿PD关节位置跟踪控制

王东云， 李继朋， 王瑷珲， 胡宁宁， 陈赛男

(1.黄淮学院， 河南 驻马店 463000；2.中原工学院 电子信息学院， 河南 郑州 450007)

自20世纪60年代第一台真正意义的工业串联机器人诞生以来，机器人的控制问题一直是机器人研究领域的重点问题。随着电子信息技术的发展和现代控制理论研究的不断深入，各种各样的机器人控制方法不断涌现。串联机器人是一个高度复杂的机电一体化系统，其动力学模型是一个多输入、多输出、强耦合且拥有许多不确定性的非线性微分方程，机器人的控制问题相当复杂[1]。现代化的工业生产过程要求机械臂具有良好的定位精度和快速的轨迹跟踪能力，因此产生了许多基于动力学模型的动态控制方案[1-2]。基于动力学模型的动态控制方案包括自适应控制、鲁棒控制、变结构控制等现代控制方法，同时也有模糊控制、神经网络控制等智能控制方法。这些控制方法解决了一些系统本身的非线性、耦合性、外部干扰以及其他不确定性问题，提高了系统的鲁棒性和控制精度[3-4]。然而，基于机械臂动力学模型的动态控制方案需要进行大量的动力学实时在线计算，且机械臂本身又是一个高度复杂的多变量、强耦合的非线性系统，需要较大的在线计算量，给机械臂的动态实时控制带来了困难[5]。在目前实际投入使用的工业串联机器人中，为简化控制难度同时能够胜任特定的工业现场，多数采用独立的PD(Proportion Differentiation)或变形的仿PD(PD-like)位置跟踪控制方案[5]。

串联机器人位置控制的目的在于，末端操作工具无论从何种起始位置出发均能实现对期望轨迹的跟踪控制。如果期望轨迹是一个点，则属于定点控制；如果期望轨迹是一条连续变化的曲线，则属于连续轨迹的跟踪控制。本文设计了一种PD-like位置跟踪控制器，在传统PD控制器的基础上引入S型曲线函数，不但提高关节角位移的收敛速度，且使关节初始力矩有一定程度的降低；并基于李雅普诺夫稳定性理论，以关于误差的二次型函数作为系统的能量函数，在考虑各关节耦合性及非线性的情况下，保证串联机器人控制系统在李雅普诺夫意义下的稳定性，使得关节角位移具有良好的跟踪性能[6-8]。

1 动力学模型的建立

工业串联机器人(见图1)的平面两连杆机械臂模型如图2所示。该两连杆串联机械臂封闭形式的动力学模型为：

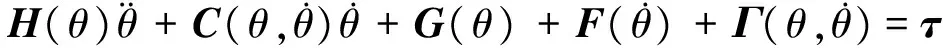
(1)

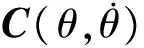
忽略重力、摩擦力及不确定性因素的影响，式(1)可改写为：

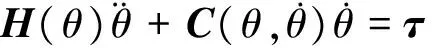
(2)

图1 工业串联机器人

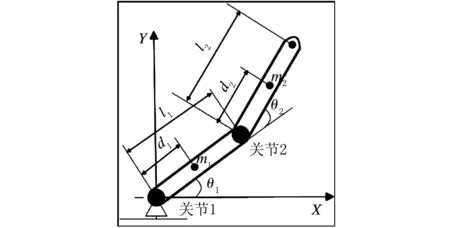
图2 平面两连杆机械臂模型 (注：参数θ1和θ2分别为连杆1和连杆2的关节角度；m1和m2分别为两个连杆的质量；l1和l2分别为两个连杆的长度；d1和d2分别为两个连杆的重心距各自关节的长度。)

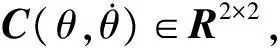
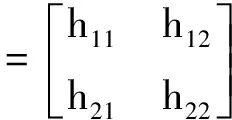
(3)

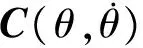
(4)

则：

(5)

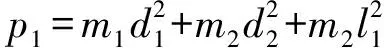
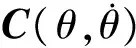
2 控制器设计

忽略机械臂所受重力和其他干扰因素作用后，两连杆机器人的动力学方程可用式(2)描述。仿PD控制时，设计控制律为：

(6)

式中：e=θd-θ为跟踪误差，θd为参考轨迹；Sp和Sd均为S型函数矩阵，且

式中：t为仿真时间；k1和k2均为函数增益；α1、α2和β1、β2均为指数函数的衰减因子；a1、a2均为指数函数的前系数。

采用定点控制时，θd取常值，有：

(7)

即

(8)

取李雅普诺夫函数为：

(9)

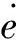
(10)

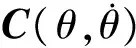
(11)

(12)

所以：

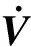
(13)

3 系统仿真与分析

以式(2)两连杆机械臂简化模型为控制对象，不考虑机械臂所受的重力、摩擦力和干扰，对式(6)控制律进行仿真。根据图2各参数标注，被控对象的物理结构参数为：m1=0.6 kg，m2=0.6 kg，l1=1.2 m，l2=0.8 m，d1=0.6 m，d2=0.4 m。

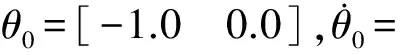
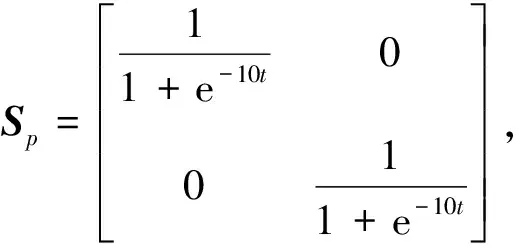
对整个闭环控制系统进行仿真。在仿真输出结果中：图3为关节角位移跟踪曲线；图4为仿PD控制器的输出，即关节力矩曲线；图5为关节角速度曲线；图6为关节角位移误差曲线。根据李雅普诺夫稳定性理论，将控制器参数调节为正，可保证控制系统渐进稳定，关节角位移能够收敛到期望位置，实现关节位置的定点跟踪控制。

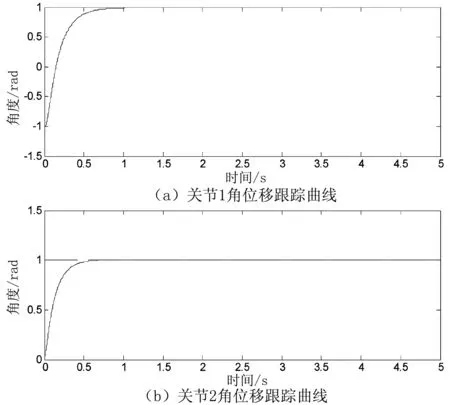
图3 关节角位移跟踪曲线

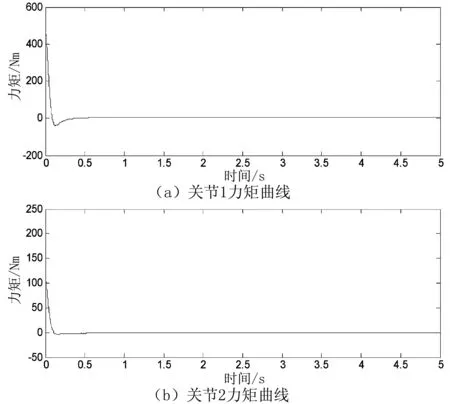
图4 关节力矩曲线

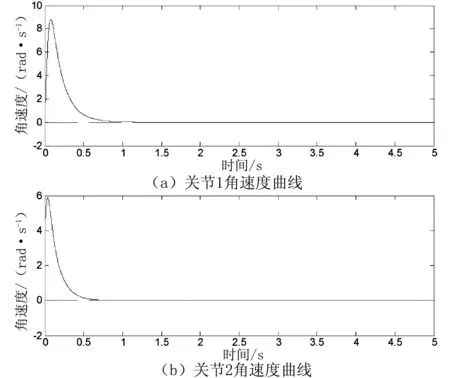
图5 关节角速度曲线

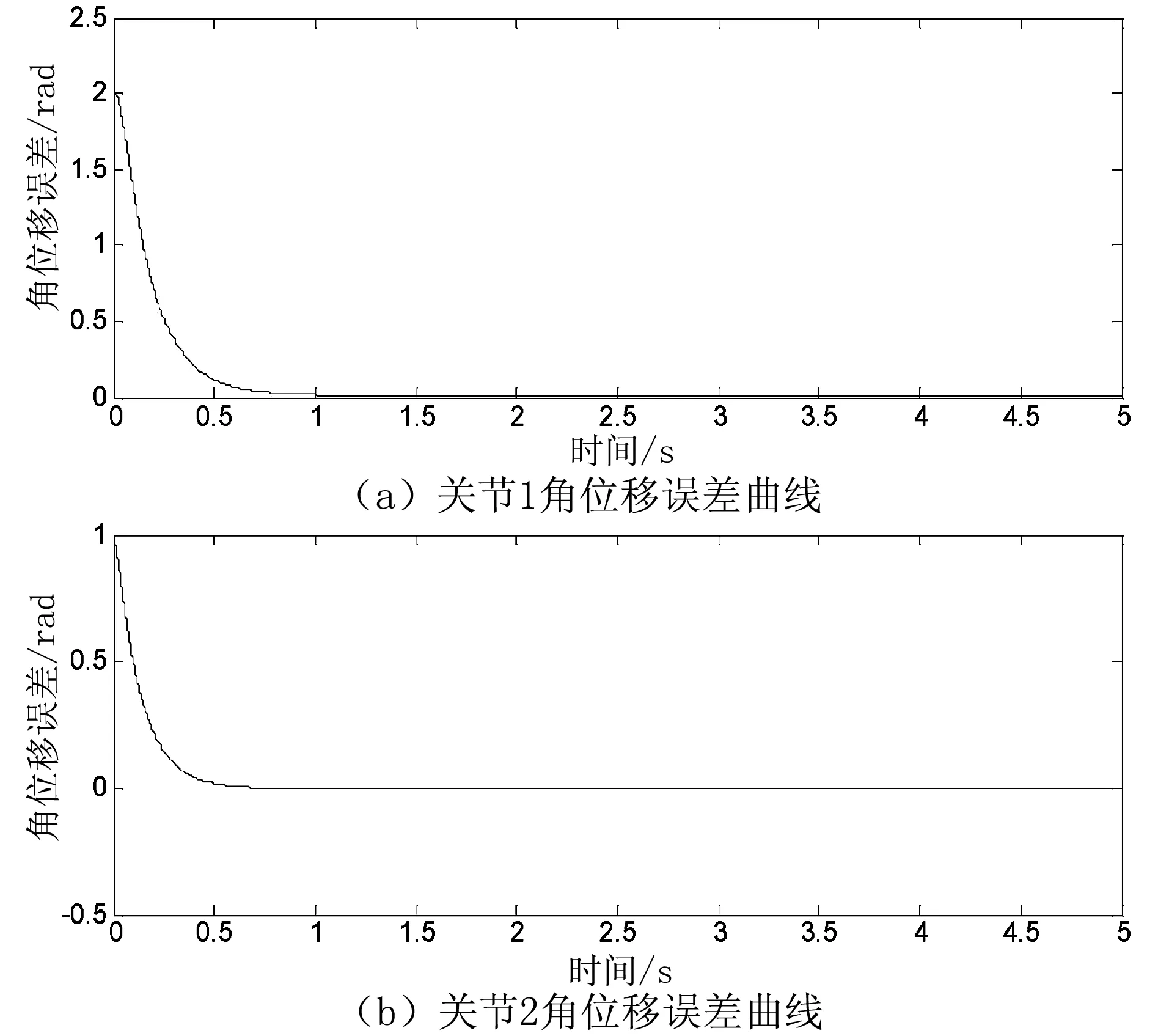
图6 关节角位移误差曲线

从图3和图6可以看出，关节角位移在0.5 s之内即可实现收敛，使得位置跟踪误差快速衰减到0，这与S型曲线函数有关；由于两连杆的耦合作用，关节1比关节2的运动速度平缓，但无论两关节从何种起始位置出发，关节速度最终均能收敛到0。从图4可以看出，两关节的初始力矩均不大，初始时刻之后，关节力矩迅速降低，直至完成动态跟踪过程，关节力矩输出为0。

4 结 语

仿真结果表明，使用仿PD控制器对机械臂进行控制，可以得到较好的控制结果。相较于传统独立的PD控制，关节角位移的跟踪速度有所提高，而且关节初始力矩有一定程度的降低。按照李雅普诺夫稳定性理论进行调节，在保证系统稳定且初始力矩不太大的情况下，机械臂各关节角位移能够快速收敛到期望位置，进而使机械臂末端操作达到定点。

[1] 霍伟.机器人动力学与控制[M].北京:高等教育出版社,2005.

[2] 王耀南.机器人智能控制工程[M].北京:科学出版社,2004.

[3] 刘金琨.机器人控制系统的设计与MATLAB仿真[M].北京:清华大学出版社,2008.

[4] 方勇纯.非线性系统理论[M].北京:清华大学出版社,2014.

[5] Wang A, Deng M. Robust nonlinear control design to a manipulator based on operator based approach[J]. ICIC Express Letters，2012，6:617-623.

[6] Dixon W E, Queiroz M S D, Zhang F, et al. Tracking control of robot manipulators with bounded torque inputs[J]. Robotica，1999，17(2)：121-129.

[7] Luca A D, Siciliano B, Zollo L. PD control with on-line gravity compensation for robots with elastic joints[J]. Automatic, 2005, 41(17): 1809-1819.

[8] 张春阳, 江先志. 六足机器人步态规划及其静态稳定性研究[J]. 成组技术与生产现代化, 2016,33(2):40-47.

(责任编辑:王长通)