复合荷载作用下重力锚的抗滑稳定计算

李飒，段高松，李怀亮，黄山田，王晓飞

(1.天津大学 建筑工程学院，天津 300072；2.中海油安装公司，天津 300456)

重力锚是一种常见的锚固形式，依靠自身锚重与锚底土的相互作用来提供锚固力，适用于小型系泊系统，重力锚由于形式简单并且经济，是使用较早的一种锚固基础形式。近年来，随着海上构筑物形式的多样化，重力锚凭借其适用范围广、经济、安装简单等特点，被广泛应用于多种结构物。Atturio等[1]针对拖动埋置锚、平板锚、桩锚以及重力锚这4种类型的锚做了参数化研究，推荐底部带有剪力键的重力锚作为海洋热能转换系统平台的系泊装置。Rodríguez等[2]针对P &D项目中海上停泊平台的选择、分析及锚泊系统的设计形成相关知识体系，从费用、竖向承载力、安装和拆除以及环境影响方面分析比较了拖动埋置锚、桩锚、吸力锚、重力锚以及螺旋锚的优缺点，分析结果显示，重力锚在以上各方面综合评价优秀，推荐其作为一种锚固形式。 Upsall等[3]指出深水浮式建筑物的锚固受水深变化、土体类别、建筑物用途以及环境荷载的影响，其设计比较了3种不同类型的锚：桩锚、重力锚、抓力锚，最终确定重力锚是一种比较好的形式。Howard等[4]在华盛顿州航线浮桥的设计过程中也选择了重力锚作为其锚固形式。一些大型船舶在海上作业时，在某些特殊环境下，比如火山环礁起源地或热带岛屿，重力锚也是一种比较好的选择[5-6]。

有关重力锚的设计计算，Taylor[7]给出了相应的选取原则和设计计算方法。美国海军工程师手册指出，对于无剪力键或裙板的重力锚[8]，其水平承载力主要靠锚底与土体之间的摩擦力来提供，在水平荷载作用下，其破坏模式主要是水平滑动破坏。针对这种破坏，在无粘性土中，重力锚的水平承载力可由式(1)计算。

F=(W-Fv)tan(φ-5°)

(1)

式中：W为锚浮重；Fv为作用在锚上竖直方向上的力(向上为正)；φ为土的内摩擦角。

近年来，有研究显示，对于重力锚的设计计算存在一些问题。李怀亮等[9]针对有关规范给出的重力锚水平承载力计算公式，采用有限元法研究了重力锚在水平力作用下的破坏机理，从而得到了在相同的工况条件下，重力锚水平承载力与其底面积有关。叶邦全[10]指出，重力锚承受水平负荷的能力取决于锚与底质之间的摩擦力以及底质的剪切强度。徐保照[11]在进行钙质土锚固基础设计研究中，用有限元方法研究了重力锚的破坏机理，从锚底土体的应变可以看到，重力锚前端土体有较大的破坏。因此，在砂土地基重力锚的设计计算过程中，有关水平滑动破坏的假定不再合理，需要针对重力锚的破坏机理进行更深入的探讨。

随着海洋开发的深入，不同海域、不同结构形式对系泊系统提出了不同的要求。特别是随着海上作业能力的增强，大型船只面临着越来越复杂的锚泊条件和锚泊要求。重力锚作为一种备选锚型，有必要对其破坏机理以及设计计算方法进行更加深入的研究。本文采用了室内模型试验的方法对这一问题进行了探讨。

1 室内模型试验

试验在港口与海岸工程试验室内进行。试验装置照片见图1。试验设备主要由模型水槽、流速控制系统、量测系统、计算机数据采集系统组成。

图1 试验装置

水槽试验段尺寸为0.88 m×0.50 m×0.2 m，水槽一侧装有有机玻璃，有机玻璃外侧安装摄像机，可以对试验过程进行记录。

重力锚模型尺寸按照原型1∶15进行制作，重力锚试件尺寸取：0.20 m×0.20 m×0.10 m，重量为213.32 N。

试验中拉力和位移数据通过拉力传感器及其配套软件自动采集到计算机中。拉力传感器采用TJL-1S型拉力传感器，量程为0～30 kg，综合精度(线性+滞后+重复性)为0.02。拉线式位移传感器型号为KS20-1000-01-C，量程0～1 000 mm，精度±0.53%。

室内模型试验用土取自中国南海，其基本物理力学指标如表1所示。

表1 砂土基本物理力学指标Table 1 Physical and mechanical indexes

为了观察锚体在滑动过程中土体的变形情况，在水槽中的试验段，纵向每隔2 cm铺设彩砂来观察重力锚的运动引起的土层的变形情况,如图2(a)所示。

图2 重力锚运动过程Fig.2 Gravity anchor movement proces

2 试验结果及分析

2.1 重力锚的滑动破坏机理

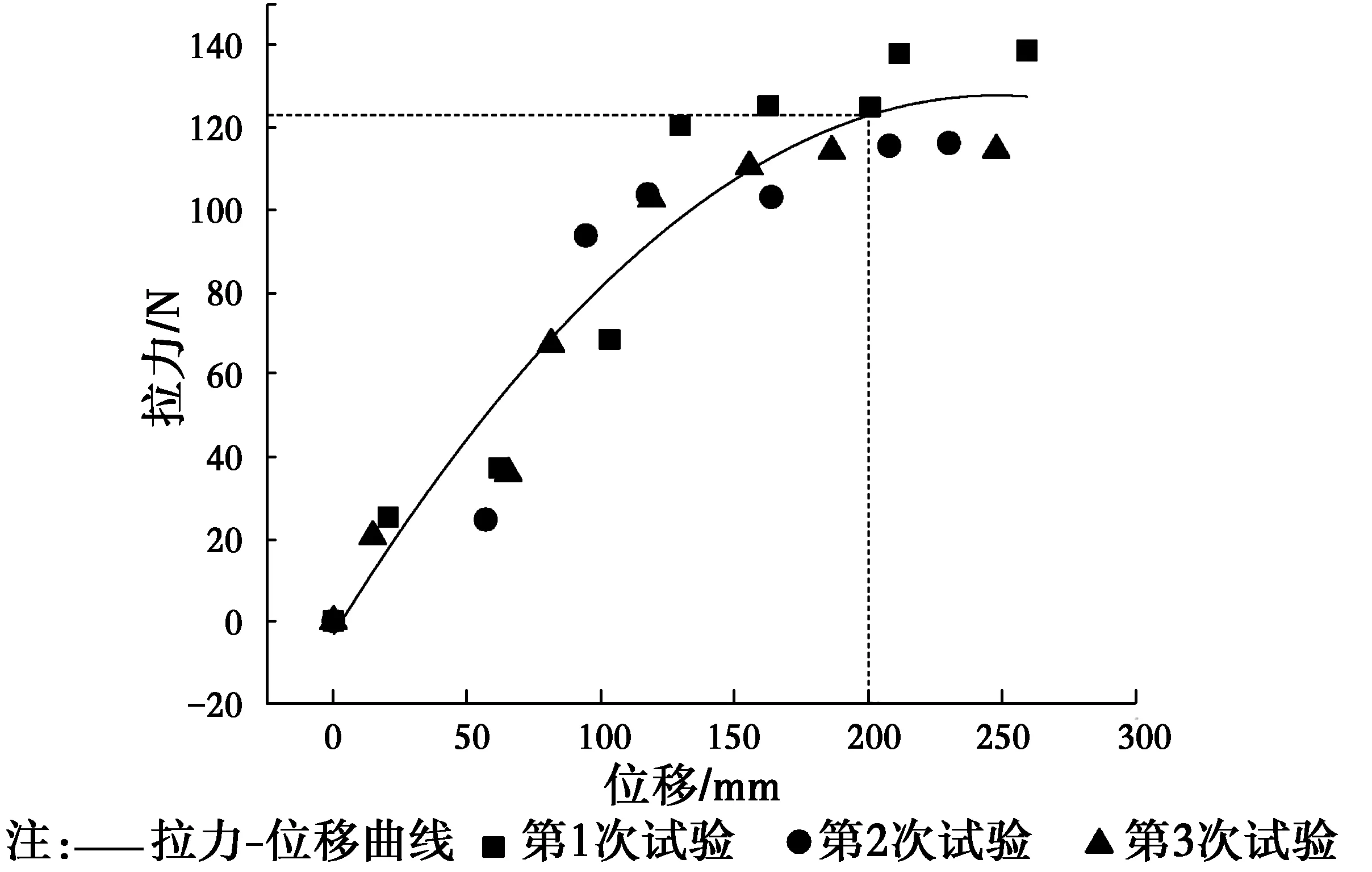
图3 拉力位移关系图Fig.3 Relationship of force-displacemen

图2为试验过程中重力锚的运动趋势以及锚下部土体的变形情况。从图中可以看到，施加拉力之前，在自重作用下，重力锚的沉降不大。随着拉力的增加，重力锚开始启动，在弯矩的作用下，重力锚前端开始下沉，同时，土体中出现较为明显的滑动面(见图2(b))；随着拉力的增加，滑动距离增大，重力锚下受扰动土体的范围进一步增大，前方土体发生较明显的隆起(见图2(c))。当重力锚的倾斜与地面达到一定角度时，水平拉力产生的弯矩与初始时反向，锚体前端抬起，当达到容许位移(本次试验的容许位移为20 cm)，锚体调平，锚底与水平面夹角几乎为0(见图2(d))。

通过上述试验过程可以得到土体的破坏过程，破坏时的滑动面示意图见图4。其中,红色标识部分为本次试验得到的土体滑动面， 图4中蓝色部分标识的滑动面为目前设计计算方法的土体滑动面。基础受力示意图如图5。将基础A点承受的水平荷载等效为底部B点承受的水平荷载和弯矩的组合。转化之后的荷载组合为表2。

表2 荷载组合Table 2 Loading combination

图4 土体破坏示意图Fig.4 Schematic of soil failure

图5 基础受力示意图Fig.5 Schematic of force analysi

从土体破坏示意图可以看到，在容许的滑动位移范围内，锚底面下的土体形成了比较完整的滑动面。造成这一现象的主要原因在于，重力锚发生滑动过程中，承受了自重(V)、水平拉力(H)、以及水平拉力导致的弯矩(M)的H-V-M的复合荷载作用。这一特征符合海洋工程结构物受力的普遍特点。

2.2 重力锚的设计计算方法

为了准确地反映重力锚的水平承载特性，结合室内模型试验结果，采用极限平衡条分法对重力锚的抗滑稳定进行了探讨。

计算过程中采用如下基本假定：地表水平，地基土为半无限空间体，土体容重为浮容重，不考虑超静孔压。为简便计，取单位长度进行二维分析。

根据极限平衡理论建立起来的条分法是在工程实践中得到广泛应用的一种方法[12]，极限平衡法以Mohr-Coulomb抗剪强度理论为基础，先设定一个滑动面，并将滑动面划分成若干条块，然后建立作用在这些条块上的力以及力矩的平衡方程，进而分析最危险滑动面及其安全系数[13]。

极限平衡法主要包括两条基本法则：1)每个条块均满足静力平衡条件；2)每个条块在滑动面上满足Mohr-Coulomb准则[14]。但是，通过该基本法则所建立的方程组是非静定的，无法通过其直接求出安全系数，因而，通常在极限平衡法中对某些多余的未知量作出一定的假设，使其变成静定问题即可求解。本文为求解上述问题，采用了如下假定：条块间的法向力与剪切力的比值用条间力函数f(x)与1个待定比例系数λ的乘积表示，该假定与morgenstern-price方法的假定相同，利用迭代的方法来计算安全系数[15-20]。

计算模式图见图6。在分析土条受力状况时，将土体分为两个区域，重力锚范围内土体和重力锚范围外土体。在重力锚范围内的土体，考虑锚底与土体的摩擦力土条的受力如图7(a)所示；在重力锚范围以外土体没有水平荷载，土条受力如图7(b)所示。土条高度为hi、宽度为bi、底面倾角为αi。

图6 滑动块体Fig.6 The sliding block

图7 典型条块

具体计算过程如下：

1)重力锚范围内的锚底土块 建立第i个条块的受力平衡，分别沿垂直与滑动面方向和平行与滑动面方向将力进行分解，推导出安全系数的表达式。

(2)

式中：Ri为除条间力之外的条块上所有力所提供的抗剪力之和；Ti为所有力产生的下滑力之和。其中

Ri=[(Wi+P)cosαi-Fhsinαi]tanφi+

cibisecαi

(3)

Ti=(Wi+P)sinαi+Fhcosαi

(4)

(5)

Φi=(sinαi-λficosαi)tanφi+

(cosαi+λfisinαi)Fs

(6)

式 (2) 为隐式方程，因为两边均出现了变量Fs，因此，需要用迭代方法求解。

考虑第i个条块的力矩平衡，在条块基底中心取力矩，根据力矩平衡方程推导出比例系数λ的表达式

(7)

计算参数如表3所示。

表3 计算参数表Table 3 Calculation parameter

容重取浮容重；抗剪强度指标c、φ取快剪试验得到的指标作为计算参数。

2)重力锚范围外的土块 锚底土块安全系数Fs与比例系数λ的推导方法相同，首先，建立第i个条块的受力平衡，分别将与滑动面垂直方向和与滑动面平行方向的力进行分解，推导出安全系数表达式(8)，然后，考虑第i个条块的力矩平衡，推导出比例系数λ的表达式(9)。

(8)

(9)

式中

Ri=Wicosαitanφi+cibisecαi

(10)

Ti=Wisinαi

(11)

(12)

Φi=(sinαi-λficosαi)tanφi+

(cosαi+λfisinαi)Fs

(13)

安全系数Fs与比例系数λ计算过程见图8。

图8 安全系数计算流程图Fig.8 Safety factor calculation flow char

安全系数和比例系数的初始迭代数值分别为1.0和0[19-20]，迭代精度控制为10-4，当两者满足收敛要求时,迭代结束得到安全系数。

在计算过程中，假定滑动面位置，进行土条划分，依据图8中安全系数计算流程图进行迭代计算，得到该滑动面条件下的安全系数值；改变滑动面位置，重复上述步骤，得到一系列滑动面及其对应的安全系数，其中,最小的安全系数即为所求的最危险滑弧对应的安全系数。

3 可靠性分析

为了验证上述方法的可靠性，利用室内模型试验的结果进行了验证。根据室内试验的结果(图3)可知，当达到容许位移时，重力锚对应的拉力为122.7 N。分别采用两种方法进行计算。

1)采用现有重力锚的设计计算方法

F=(W-Fv)tan(φ-5)

计算得到的重力锚水平承载力为97 N，误差为21%。

2)本文提出的方法 根据本文提出的方法，施加水平力122.7 N，得到最小安全系数为0.96。也就是说，其极限抗滑力为117.8 N，误差为4%。

与现有重力锚设计计算方法相比，本文提出的方法计算精度提高了约17%。导致该差异的主要原因在于，目前的设计计算方法建立在重力锚的水平承载力为重力锚与地基界面摩擦力控制的基础上，这一机理对于容许一定位移量的重力锚，明显偏于保守。本文提出的方法由于考虑了重力锚的滑动过程，在容许的位移范围内，得到的结果更加符合实际。

4 结论

通过室内模型试验模拟重力锚在砂土上的运动过程，采用条分法计算重力锚的水平承载力，得出以下结论：

1)作为船舶等浮体结构的临时锚固基础，重力锚在承受水平拉力发生滑动时，在土体当中形成了贯通的滑动面，滑动面的形状近似为圆弧。

2)采用条分法进行复合荷载作用下的重力锚抗滑稳定分析与重力锚的滑动机理相吻合。

3)采用本文的方法得到的重力锚水平极限承载力与试验结果非常接近。与传统的方法相比，计算精度提高了约17%。

4)对于船体等可容许一定范围位移的结构来说，传统的重力锚设计计算方法偏于保守。

[1] ATTURIO J, VALENT P. High-capacity, deep-water, free- fall anchor [J]. Oceans,2011,9:592-596.

[3] UPSALL B, HORVITZ G, RILEY B, et al. Geotechnical design: deep water pontoon mooring anchors[C]// Ports '13: Triennial International Conference, 2013:1077-1086.

[4] HOWARD T，RILEY B，UPSALL B，et al. Structural design of deep water pontoon mooring anchors [C]// Ports '13: Triennial International Conference. 2013: 1087-1096.

[5] HARRIS R E，JOHANNING L，WOLFRAM J. Mooring systems for wave energy converters: A review of design issues and choices [J]. Journal of Engineering for the Maritime Environment，2006，22(12): 159-174.

[6] UPSALL B，HORVITZ G，RILEY B，et al. Geotechnical design: Deep water pontoon mooring anchors [C] // Proceedings ports 2013: Success through diversification, USA: ASCE，2013:1087-1096.

[7] TAYLOR R J. Interaction of anchors with soil and anchor design [R]. California：Naval Civil Engineering Lab, 1982.

[8] SEIBERT M G. Determining anchoring systems for marine renewable energy devices moored in a western boundary current [D].Florida Atlantic University,2011.

[9] 李怀亮，黄山田，王晓飞，等.重力锚水平承载力特性的 有限元分析[J].中国港湾建设, 2016, 36(1):6-9.

LI H L，HUANG S T，WANG X F，et al. Finite element analysis on horizontal bear capacity charac-teristic of gravity anchor [J]. China Harbour Engineering，2016, 36(1):6-9. (in Chinese)

[10] 叶邦全.海洋工程用锚类型及其发展综述[J].船舶与海洋工程, 2012(3):1-7.

YE B Q. The anchor type in ocean engineering and its development review [J]. Naval Architecture and Ocean Engineering, 2012(3):1-7. (in Chinese)

[11] 徐保照.钙质土中锚固基础设计研究[D].天津:天津大学, 2014.

XU B Z. The design and study of anchorfoundation in calcium soil [D]. Tianjin:Tianjin University, 2014. (in Chinese)

[12] 陈祖煜.土坡稳定分析通用条分法及其改进[J].岩土工程学报, 1983, 5(4):11-27.

CHEN Z Y. The generalized method of slices for slope stability analysis and its modifications [J]. Chinese Journal of Geotechnical Engineering, 1983, 5(4):11-27. (in Chinese)

[13] 徐卫亚,周家文,石崇,等.极限平衡分析中加固力对岩质边坡稳定性的影响[J].水利学报, 2007, 38(9):1056-1065.

XU W Y, ZHOU J W, SHI C. Effect of streng- thening force on rock slope stability in limit equilibrium analysis [J]. Journal of Hydraulic Engineering, 2007, 38(9): 1056-1065. (in Chinese)

[14] 黄梦宏,丁桦.边坡稳定性分析极限平衡法的简化条件[J].岩石力学与工程学报, 2006, 25(12):2529-2536.

HUANG M H, DING H. Some assumption conditions of limit equilibrium method for slope stability analysis [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(12):2529-2536. (in Chinese)

[15] 魏海楠,巨能攀.Morgenstern-Price方法的遗传优化求解过程[J].地下空间与工程学报, 2014, 10(Sup2): 1958-1962.

WEI H N，JU N P. Genetic optimization algorithm for Morgenstern-Price Method [J]. Chinese Journal of Underground Space and Engineering, 2014,10(Sup2): 1958-1962. (in Chinese)

[16] MORGENSTERN N R，PRICE V E. The analysis of the stability of general slip surfaces [J]. Geotechnique，1965，15(1)：79-93.

[17] CHEN Z Y, MORGENSTERN N R. Extensions to the generalized method of slices for stability analysis [J]. Canadian Geotechnical Journal, 1983, 20(1):104-119.

[18] ZHU D Y, LEE C F, QIAN Q H, et al. A new procedure for computing the factor of safety using the Morgenste [J]. Canadian Geotechnical Journal, 2001, 38(4):882-888.

[19] 胡辉,董梅,姚磊华.非微分Morgenstern- Price法在边坡稳定分析中的应用[J].桂林理工大学学报, 2008, 28(3):344-348.

HU H，DONG M，YAO L H. Application of non- differential form of Morgenstern-Price Method in slope stability analysis [J]. Journal of Guilin University of Technology，2008, 28(3):344-348. (in Chinese)

[20] 朱大勇,李焯芬,黄茂松,等.对3种著名边坡稳定性计算方法的改进[J].岩石力学与工程学报, 2005, 24(2): 183-194.

ZHU D Y，LEE C F，HUANG M S，et al. Modifications to three well-known methods of slope stability analysis [J]. Chinese Journal of Rock Mechanics and Engineering，2005, 24(2):183-194. (in Chinese)