棒状铁镓合金磁滞特性和功耗特性分析

翁 玲 曹晓宁 梁淑智 孙 英 黄文美 王博文

(河北工业大学省部共建电工装备可靠性与智能化国家重点实验室， 天津 300130)

0 引言

铁镓合金是新型磁致伸缩换能器能量转换的关键部分，其磁滞特性及功耗特性对换能器的工作效率尤为重要[1-4]。目前，科研人员对磁性材料的磁滞特性和功耗特性进行了大量的研究，文献[5]提出了一种模拟电工钢片复杂磁特性的矢量磁滞模型，考虑频率、磁化历史等因素对磁滞特性的影响，但该磁滞模型数学表达式复杂，不适于工程实践。文献[6]介绍了静态和动态磁滞模型，将二阶低通滤波器插入J-A数学模型，近似模拟高频动态磁滞回线，但没有考虑磁参数的变化情况。文献[7]提出了一种利用局部磁滞回线特性进行无损检测新方法，研究了变励磁条件下局部磁滞回线的形成机理，并进行了仿真和实验验证。文献[8]提出了一种用于电机损耗精细化分析的分段变系数铁耗计算模型，对磁滞、涡流及剩余损耗进行准确分离，实现铁耗精细化分析，但所提模型只能在特定范围内与实测值吻合，不具有普遍应用性。文献[9]从电场、磁场和机械应力场三场耦合角度建立磁滞模型，并通过实验验证了模型的正确性和实用性。文献[10]基于J-A磁滞模型，从能量平衡原理出发，建立了以磁通密度作为输入量的铁芯动态磁滞损耗模型，但理论与实测值存在一定误差，应该对模型进行修正。文献[11]基于3D磁场解析模型，计算了无铁芯绕组的涡流损耗，并通过实验验证发现，该模型比传统经验公式更接近于实际。

本文首先基于霍尔效应和法拉第电磁感应原理，运用霍尔芯片和固定线圈法间接测量铁镓合金棒的磁场强度和磁感应强度，通过数据采集卡自动绘制不同频率和不同磁感应强度下的磁滞回线；然后根据磁滞回线，分析剩磁和矫顽力随频率和磁感应强度的变化情况；最后，利用数据采集卡上的数据计算不同磁场频率下的电磁损耗，基于Berttotti损耗模型，利用曲线拟合的方法将电磁损耗进行分离。

1 测量原理和模型

电磁损耗是磁性材料在交变磁场作用下产生的各种能量损耗的统称。在正弦交变磁场H条件下，磁感应强度B的变化也为正弦，但由于磁滞效应两者之间存在相位差，则

H=Hmcos(ωt)

(1)

B=Bmcos(ωt-δ)

(2)

式中Hm——磁场强度峰值

Bm——磁感应强度峰值

δ——相位差ω——角频率

关于磁场强度的测量基于霍尔原理采用霍尔芯片进行测量。由霍尔效应可知

(3)

将B=u0H代入式(3)得

(4)

式中I——流过霍尔芯片的电流

UH——霍尔芯片感应出的电动势

RH——霍尔系数

D——霍尔芯片厚度

u0——真空磁导率

采用固定线圈法对磁感应强度进行测量，在铁镓棒上绕制一定匝数的线圈。当铁镓棒外加磁场变化时，线圈中的磁通量就会改变，由法拉第电磁感应定律得

(5)

对式(5)两边同时积分得

(6)

式中φ——铁镓棒上线圈磁通量

N——铁镓棒上线圈匝数

S——铁镓棒横截面积

e——铁镓棒上线圈感应电压

利用式(4)、(6)得到铁镓合金棒的磁场强度、磁感应强度和损耗角(磁感应强度与磁场强度的相位差)，利用上述3个物理量对铁镓棒的电磁损耗和磁能存储能力进行分析。

单位体积电磁损耗[12]

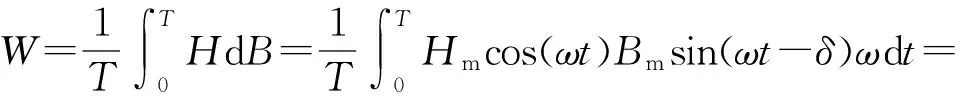
(7)

单位质量电磁损耗

(8)

单位体积介质储能[13]

(9)

单位质量介质储能

(10)

式中f——磁场频率ρ——材料密度

电磁损耗的分离模型多种多样，目前应用最为广泛的是意大利学者Berttotti总结提出的损耗分离法[14]。在正弦交变磁场下，单位质量的电磁损耗由磁滞损耗Ph、涡流损耗Pe和剩余损耗Pc组成

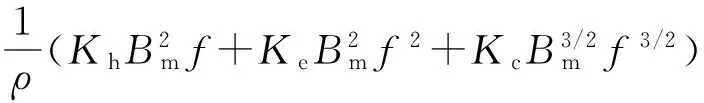
(11)

式中Kh——磁滞损耗系数

Ke——涡流损耗系数

Kc——剩余损耗系数

对于低频磁场而言，电磁损耗与频率呈指数关系

P=ea+bf

(12)

利用式(11)对电磁损耗进行分离，需对式(12)进行泰勒展开，忽略高次项得

(13)

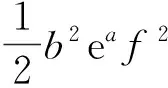
涡流损耗可以通过涡流截止频率来反映[15]，涡流截止频率越高，涡流损耗越小。

(14)

式中fc——涡流截止频率

ρ′——材料电阻率

ur——材料相对磁导率

d——材料切片厚度

2 实验平台

本实验的测试系统由4部分构成：施加磁场部分、信号检测部分、信号采集部分和数据处理部分。施加磁场部分包括：信号发生器、功率放大器和励磁线圈，其中的励磁线圈主要由导磁回路、线圈、不锈钢螺栓和不锈钢帽构成。信号测量部分包括：磁通计和霍尔芯片。霍尔芯片用来采集铁镓棒上的磁场强度，磁通计通过绕在铁镓棒上的线圈来采集铁镓棒上的磁感应强度。信号采集部分为数据采集卡，数据采集卡相当于示波器，用来采集霍尔芯片上的磁场强度波形和磁通计上的磁感应强度波形。数据处理部分为PC机上的软件，数据采集卡将采集的数据传送到PC机上，软件可以绘制H-t图、B-t图和B-H图。测量系统结构如图1所示。

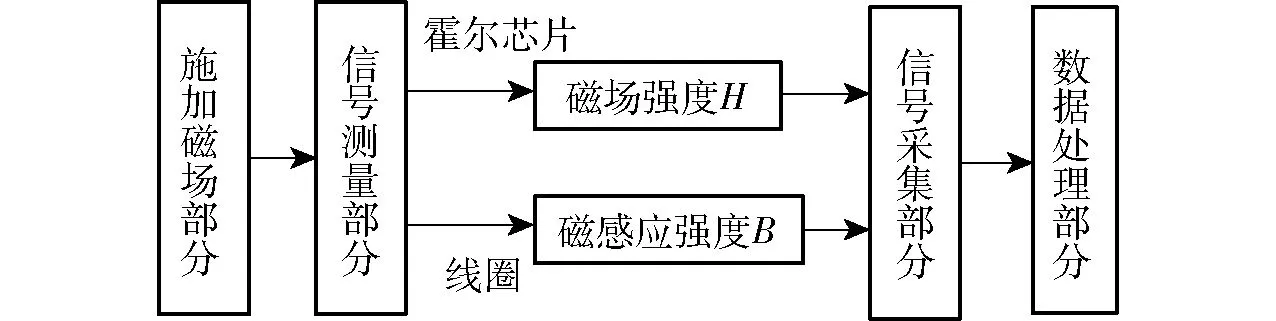
图1 测试系统结构图Fig.1 Structure diagram of testing system

施加磁场部分的工作原理：由信号发生器产生特定频率的正弦波，通过功率放大器将其放大，功率放大器的输出端接到励磁线圈上，在励磁线圈的周围产生了正弦交变磁场，交变的磁场通过硅钢片将磁场导入到铁镓棒中。励磁线圈的结构如图2所示，由上(下)不锈钢帽、上(下)导磁体(硅钢片叠加而成)、线圈(采用AWG19型号漆包线绕制而成，线径0.912 mm。每个线圈有525匝，内径30 mm，外径100 mm)和铁镓材料放置区构成。导磁回路部分由40片厚度0.5 mm的硅钢片叠加而成，是励磁线圈磁路的主要部分。为了使励磁线圈产生的励磁磁场尽可能多地分布在导磁回路上，减少漏磁，采用螺栓和铝板将上下导磁回路模块连成一个整体的回路。左右2个线圈套在铝板上，产生方向相同磁场，磁力线在铁镓合金棒处汇集。通过预先的切割使得叠加后的上、下回路模块中部各有一个直径15 mm的孔洞，以便上不锈钢帽和下不锈钢帽伸入导磁回路模块直径15 mm的孔中与铁镓合金棒粘接，形成一个完整的磁路。

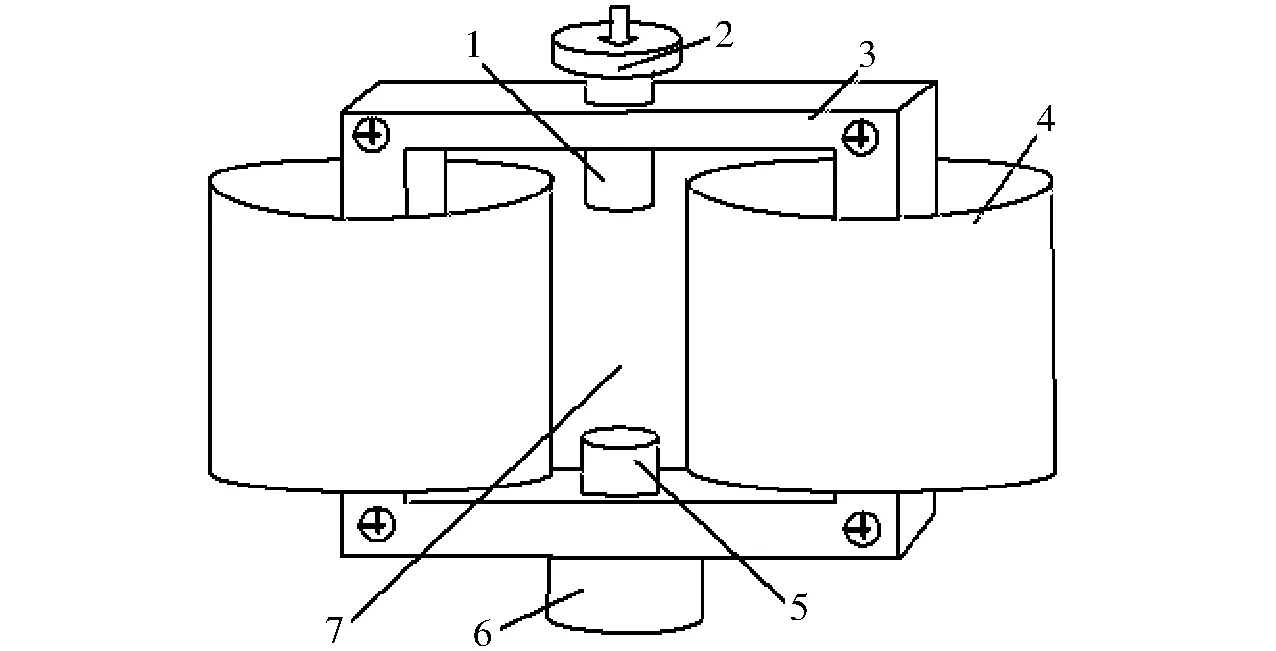
图2 励磁线圈的结构图Fig.2 Structure diagram of excitation coil1.上导磁体 2.上不锈钢帽 3.导磁回路 4.线圈 5.下导磁体 6.下不锈钢帽 7.铁镓棒放置区

信号检测部分的工作原理：对于铁镓棒上磁场强度的测量，采用A1321LUA型霍尔芯片，该芯片可以测量10-7～10 T范围内的恒定磁场，也可测量频率为1 Hz～100 MHz、磁感应强度达5 T的交变磁场，以及脉冲持续时间为几十微秒的脉冲磁场，尤其在小间隙空间内磁场的测量上具有显著的优越性[16-17]。利用式(4)计算出磁场强度。对于铁镓棒上磁感应强度的测量，采用固定线圈法，利用式(6)计算出磁感应强度。固定线圈法既可用于测量恒定磁场，也可用于测量交变磁场。

信号采集部分由数据采集卡完成，该采集卡包括上、中、下3个模块，上层为液晶显示控制模块，中层为单片机模块，下层包括USB采集卡和运放电路模块，同时USB采集卡模块外接PC机。数据采集卡的结构如图3所示。液晶显示控制模块主要功能是驱动屏幕，显示波形数据，判断触摸点位，传输触摸信号至液晶显示控制器和单片机。单片机模块主要对数据采集卡进行控制。运放电路模块和USB采集卡功能分别是放大信号和接收信号并传输至单片机和PC机。

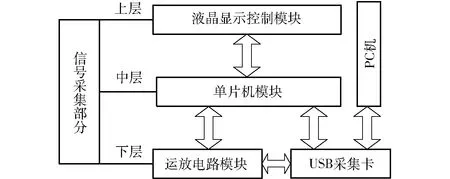
图3 数据采集卡结构图Fig.3 Structure diagram of data acquisition card

数据处理部分是软件Sysdbg 32(采用Visual Studio 2008与Matlab混编而成)，实时将采集数据的波形显示在计算机上，并在结束采集后将数据转化为txt文件或excel文件保存。通过调用Matlab程序可以绘制相应的磁滞回线。图4为测试系统的实物图。

图4 测试系统实物图Fig.4 Real picture of testing system1.数据采集卡 2.磁通计 3.信号发生器 4.功率放大器 5.压片机 6.励磁线圈 7.计算机 8.霍尔芯片

3 实验结果及分析

首先分析了铁镓合金棒的动态磁滞回线，从磁滞回线得到了矫顽力和剩磁2个重要的磁特性参数，然后分析了2种不同条件下磁滞曲线的变化情况：相同磁感应强度下不同磁场频率和相同磁场频率下不同磁感应强度。最后，通过式(8)、(10)计算出相应的电磁损耗和介质储能，根据电磁损耗机理，将其分为磁滞损耗、涡流损耗和剩余损耗，并利用式(11)、(13)对电磁损耗进行分离，分析了不同磁场频率下各损耗占总电磁损耗的比例，并对铁镓换能器工作在高频时，提出了减小涡流损耗的措施。

3.1 不同磁场频率下的磁滞特性

图5为在磁感应强度为1 725 mT，交变励磁磁场频率分别为30、40、50、60、70 Hz情况下测得的一组动态磁滞回线。由图5可见，动态磁滞曲线为不规则椭圆形，当励磁磁场频率增加，磁滞曲线横向变宽，面积不断增大，相应的电磁损耗也越大。在相同的磁感应强度下，磁场频率越高，所需的磁场强度越大，说明磁场频率的增加促进了铁镓合金中磁畴转动和磁畴壁移动，使得磁场能量损耗增加，故所需磁场强度也要相应的增大。铁镓合金棒在不同磁场频率下曲线AB基本重合，说明在频率变化不大的情况下，磁感应强度的大小主要受磁场强度的影响。曲线BC则不再重合，而是磁场频率高的曲线越不容易下降，说明磁场频率越高，铁镓合金棒中磁畴的平均动能越高，磁介质中的储能也越大，当外界磁场下降时，相应的磁感应强度下降也越慢。

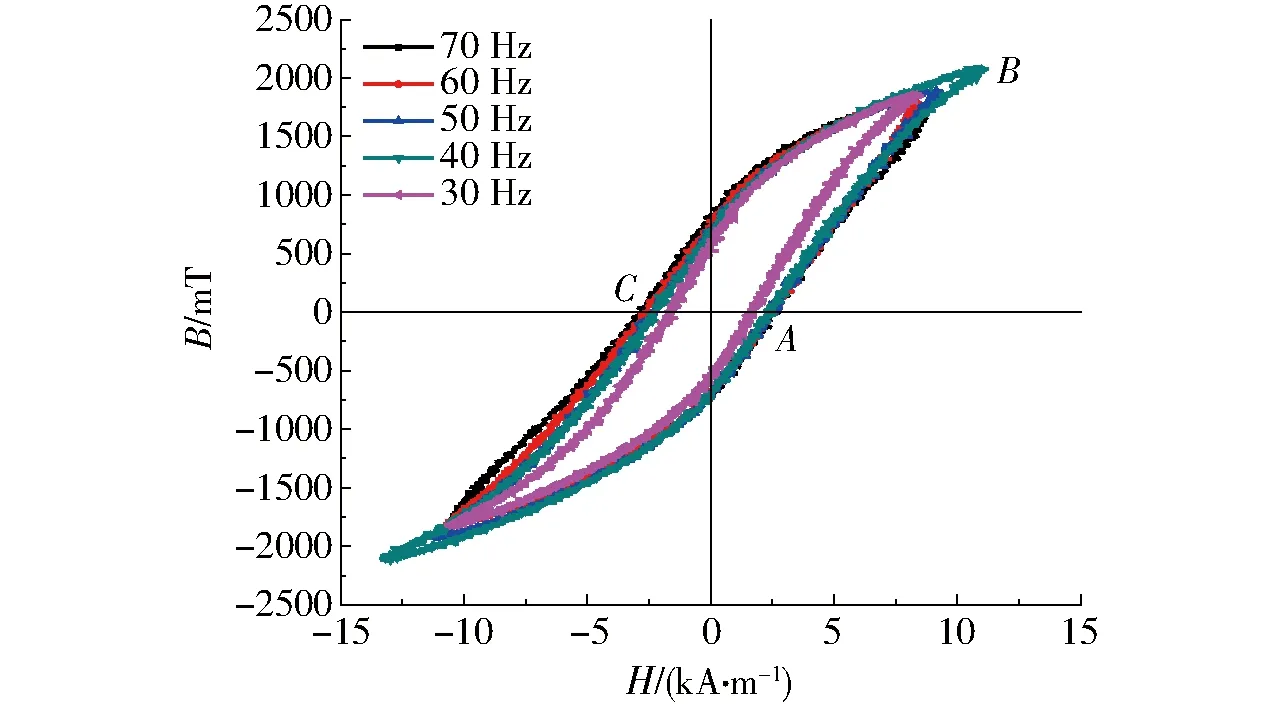
图5 不同频率下的动态磁滞曲线Fig.5 Dynamic hysteresis curved under different frequencies

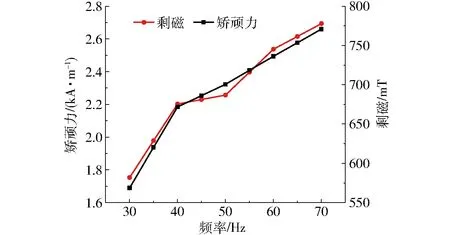
图6 不同频率下的剩磁和矫顽力Fig.6 Remanence and coercivity under different frequencies

图6为磁感应强度为1 725 mT，交变励磁磁场频率分别为30、35、40、45、50、55、60、65、70 Hz情况下测得的矫顽力分别为1.753、1.978、2.202、2.230、2.257、2.397、2.537、2.615、2.693 kA/m，剩磁分别为568.7、620.3、671.8、686.2、700.6、718.4、736.2、753.5、770.7 mT。由图6可见，随着磁场频率增加，铁镓合金棒的矫顽力和剩磁都增大。矫顽力随磁场频率的增长率呈下降趋势，在30～40 Hz频率段上增长率最大，在40～70 Hz频率段上近似线性增加。矫顽力来源于不可逆磁化过程，说明磁场频率越高，不可逆磁化程度越大，相应的矫顽力越大。剩磁随磁场频率的增加，增长率呈波动性下降趋势，在30～40 Hz频率段上增长率最大，40～50 Hz频率段上增长率最小，50～70 Hz频率段上增长率不断减小，说明剩磁对低频磁场变化敏感。

3.2 不同磁感应强度下的磁滞特性

图7为励磁磁场频率为70 Hz，磁感应强度分别为785、1 000、1 160、1 500、1 725 mT测得的一组动态磁滞回线。由图7可见，动态磁滞曲线为一系列同心椭圆，当磁感应强度增加，磁滞曲线拉伸变宽变高，面积不断增大，相应的电磁损耗也越大。相同励磁频率、不同磁感应强度下的动态回线顶点连成的线称为动态磁化曲线[18-19]。由动态磁化曲线可以看出，随着磁场强度增加，磁感应强度也相应增加，但增长速率越来越慢，当磁场强度达到7 kA/m，磁感应强度对应1.5 T时，动态磁化曲线达到饱和点，再增加磁场强度，磁感应强度变化不大。与静态铁镓合金曲线相比，饱和点处的磁场强度和磁感应强度都相应增加，说明在动态磁场的作用下，磁畴的转动和磁畴壁的移动程度加剧，铁镓介质中消耗的能量增加，要想达到饱和点，需要外界提供更大的磁场强度。

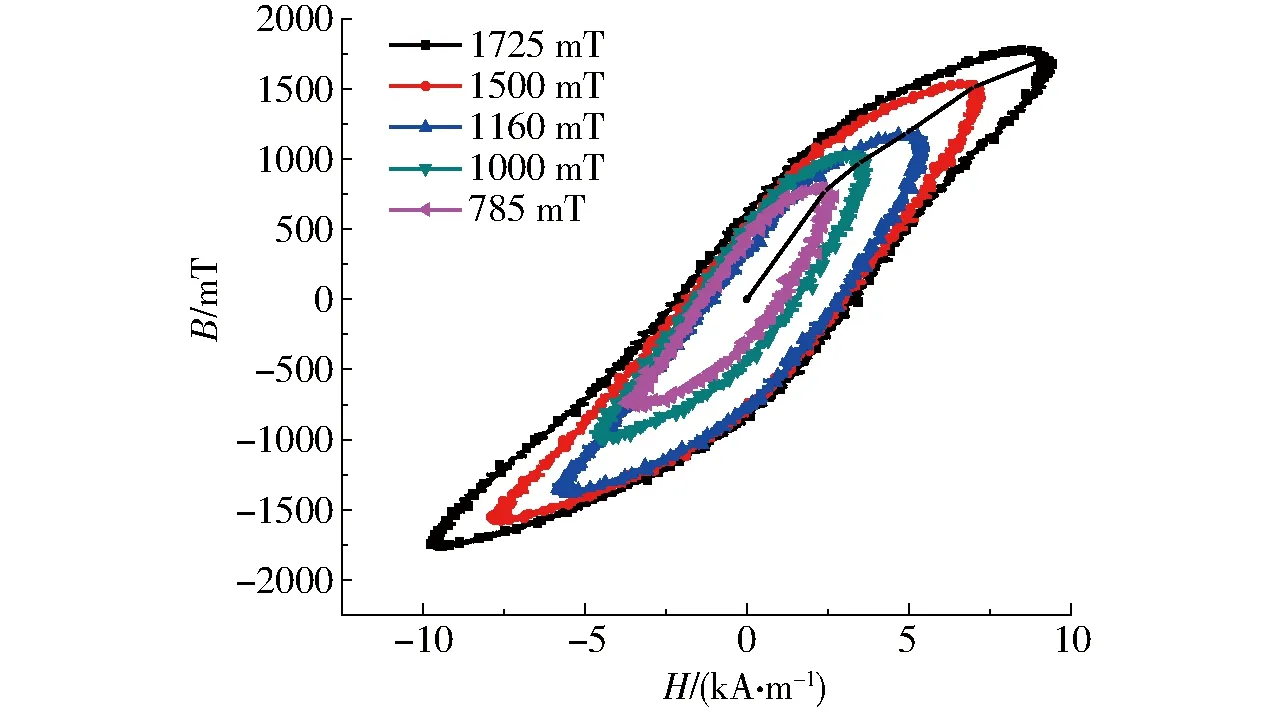
图7 不同磁感应强度下的动态磁滞曲线Fig.7 Dynamic hysteresis curves under different magnetic induction intensities

图8为励磁磁场频率为70 Hz，磁感应强度分别为785、890、1 000、1 080、1 160、1 330、1 500、1 610、1 725 mT测得的矫顽力分别为1.022、1.268、1.522、2.158、2.800、2.890、3.020、3.123、3.230 kA/m，剩磁分别为331.5、376.1、420.7、455.8、491.2、515.4、539.5、555.2、570.9 mT。由图8可见，随着磁感应强度增加，铁镓合金棒的矫顽力和剩磁都增大。矫顽力随磁感应强度的增加，增长率先快速增加之后趋于平缓，在1 000～1 160 mT矫顽力增幅最大，在1 160～1 725 mT矫顽力增幅趋于平缓。说明在较高的磁感应强度下，矫顽力受其影响较小。剩磁随磁感应强度的增加，增长率呈下降趋势，在785～1 160 mT增长率最大且呈线性增加，在1 160～1 725 mT增长率减小仍呈线性增加，说明剩磁在磁感应强度较低的情况下，受其影响较大；在磁感应强度较高的情况下，受其影响较小。

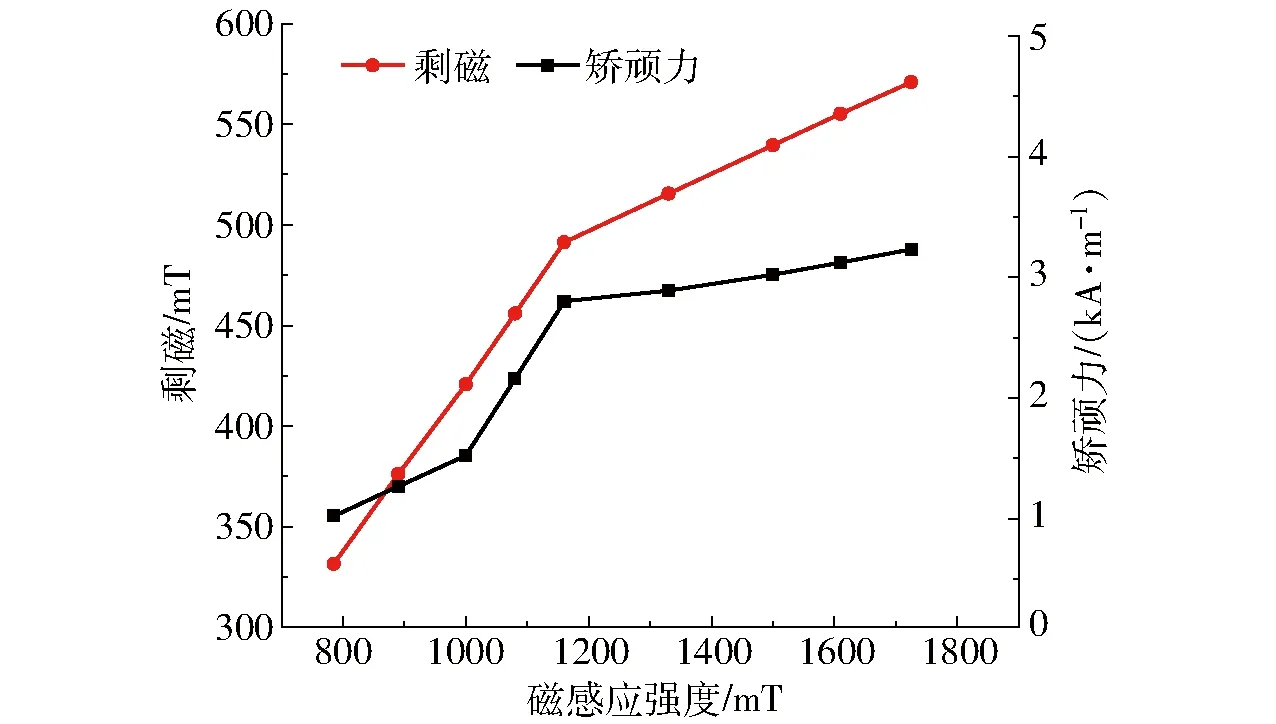
图8 不同磁感应强度下的剩磁和矫顽力Fig.8 Remanence and coercivity under different magnetic induction intensities

3.3 不同频率下的功耗特性

图9为式(8)、(10)在磁感应强度为1 725 mT，不同磁场频率时计算的电磁损耗和介质储能。由图9可见，随着磁场频率的增加，铁镓合金棒的电磁损耗和介质储能均增加，但电磁损耗增加的幅度要远大于介质储能增加的幅度。说明在动态强磁场磁化的过程中，磁场提供的能量大部分消耗在不可逆磁畴壁之间转动和移动过程中的摩擦和碰撞，而只有很少部分能量被磁畴自身吸收转化为磁畴运动的动能上，提高了磁畴运动速度，促进了磁畴在外加磁场的重新排列。由式(8)可知，在一定频率范围内，损耗角、最大磁场强度以及最大磁感应强度变化不大，因此电磁损耗可以近似看作磁场频率的指数函数关系，磁场频率的变化对电磁损耗的大小起着关键的作用。

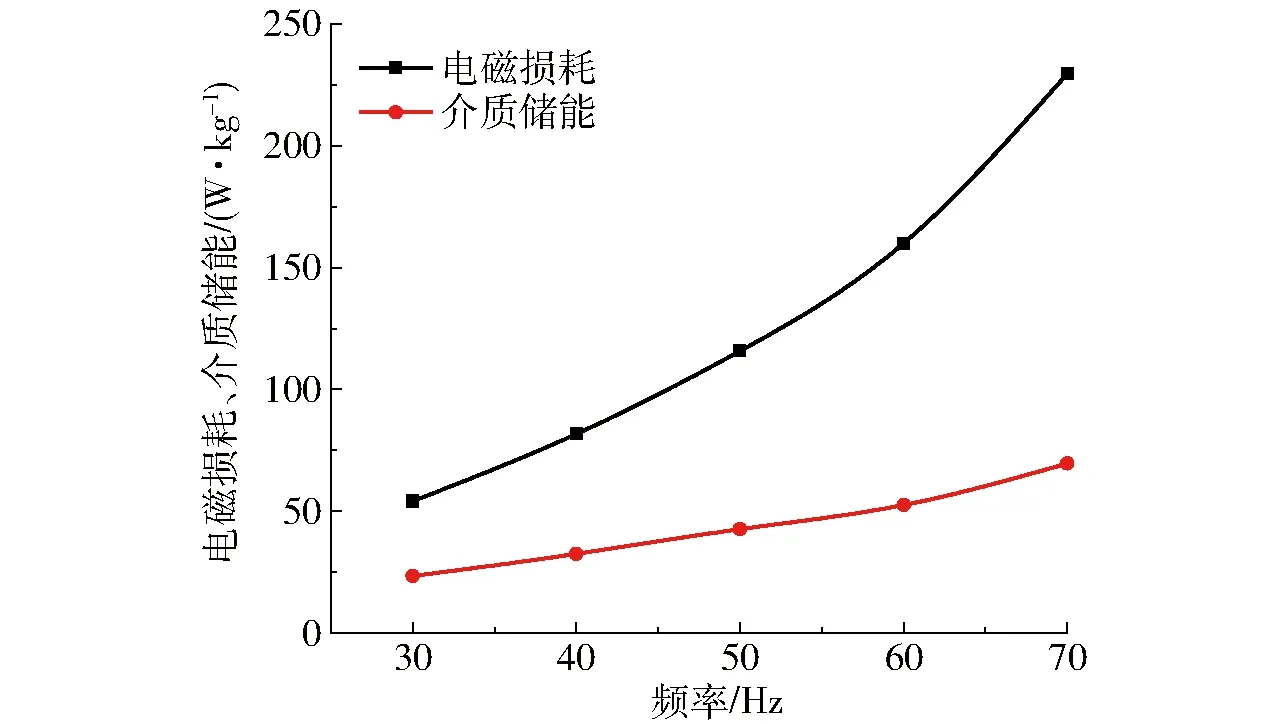
图9 不同频率下电磁损耗和介质储能Fig.9 Electromagnetic loss and energy storage media under different frequencies

图10为利用图9实验结果得到的电磁损耗和介质储能所占比例与磁场频率的关系。由图10可以看出，在磁感应强度一定时，随着磁场频率的增加，电磁损耗所占的比例不断增加，介质储能所占的比例不断下降。说明随着磁场频率的增加，不可逆磁畴运动加剧，相互之间的摩擦和碰撞频率加快，使得电磁损耗所占的比例增加；不可逆磁畴壁之间由于碰撞频率加快，对应的磁畴平均动能减少，相应的介质储能所占比例下降。

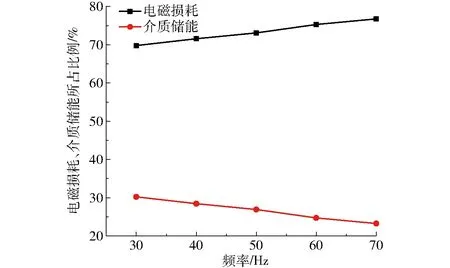
图10 电磁损耗和介质储能所占比例关系Fig.10 Proportion of electromagnetic loss and energy storage medium

图11为利用式(13)与曲线拟合法，对磁感应强度为1 725 mT的电磁损耗进行分离，得到了不同频率下的磁滞损耗、涡流损耗和剩余损耗。由图11可见，随着磁场频率的增加，涡流损耗迅速增加，剩余损耗快速增加，磁滞损耗线性增加。动态磁化过程的电磁损耗为单位质量的被测样品经过一周转动磁化后的能量损耗，包含磁滞损耗、涡流损耗和剩余损耗。由式(11)可知，在动态交变磁场条件下，磁滞损耗主要与磁感应强度有关，涡流损耗主要与磁场频率有关，剩余损耗与磁场频率和磁感应强度都有关。磁滞损耗原于磁性材料中的不可逆磁化过程，随着磁场频率的增加，不可逆磁畴的转动和磁畴壁的移动程度增加，损耗的能量增大，相应的磁滞损耗也增大。在动态磁场作用下，磁性导体内由电磁感应产生涡流，使磁体发热，即涡流损耗[20-21]。涡流损耗实质是由磁性材料引起的欧姆损耗，与磁感应强度的变化率有关，而磁场频率越高，磁感应强度变化率越大，产生的感应电压和感应电流也越大，对应的涡流损耗也越大。剩余损耗主要由磁畴壁共振和自然共振引起，与磁材料特性和工作频率有关，磁场频率越高，对应的剩余损耗也越大。

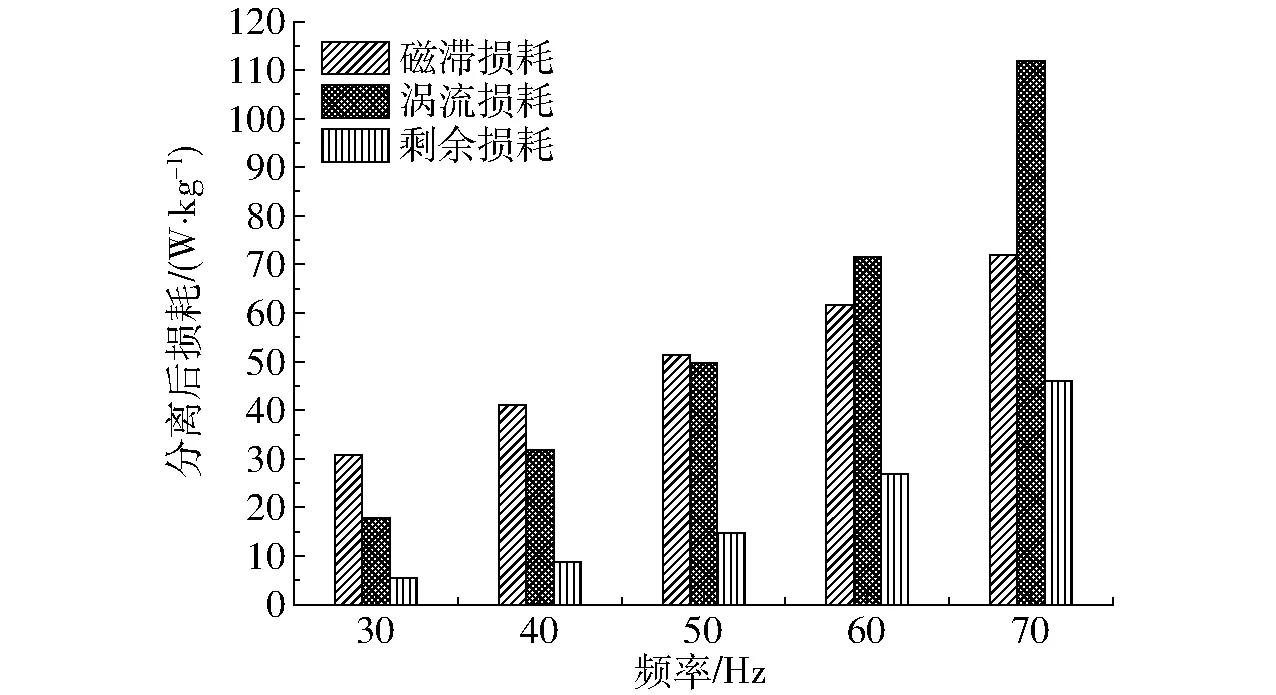
图11 分离后的3种损耗Fig.11 Three kinds of losses after separation

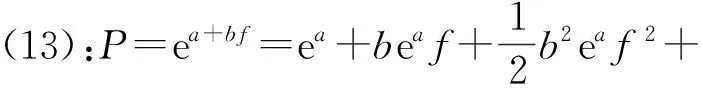
图12分析了在不同磁场频率下，磁滞损耗、涡流损耗和剩余损耗占电磁损耗的比例情况。由图12可见，随着磁场频率的增加，涡流损耗所占的比例迅速上升，磁滞损耗所占的比例不断下降，剩余损耗所占的比例略有上升。说明对于铁镓合金棒而言，在低频磁场时，磁滞损耗是电磁损耗的主要部分；在高频磁场时，涡流损耗是电磁损耗的主要部分，对电磁损耗起决定作用。对于剩余损耗而言，在30～50 Hz其所占比例基本不变，但在50～70 Hz其所占比例又略有上升，原因在于磁场频率较高时，达到了铁镓合金磁畴壁共振频率，加剧了磁畴壁之间的摩擦和碰撞，使得剩余损耗所占比例略有提高。

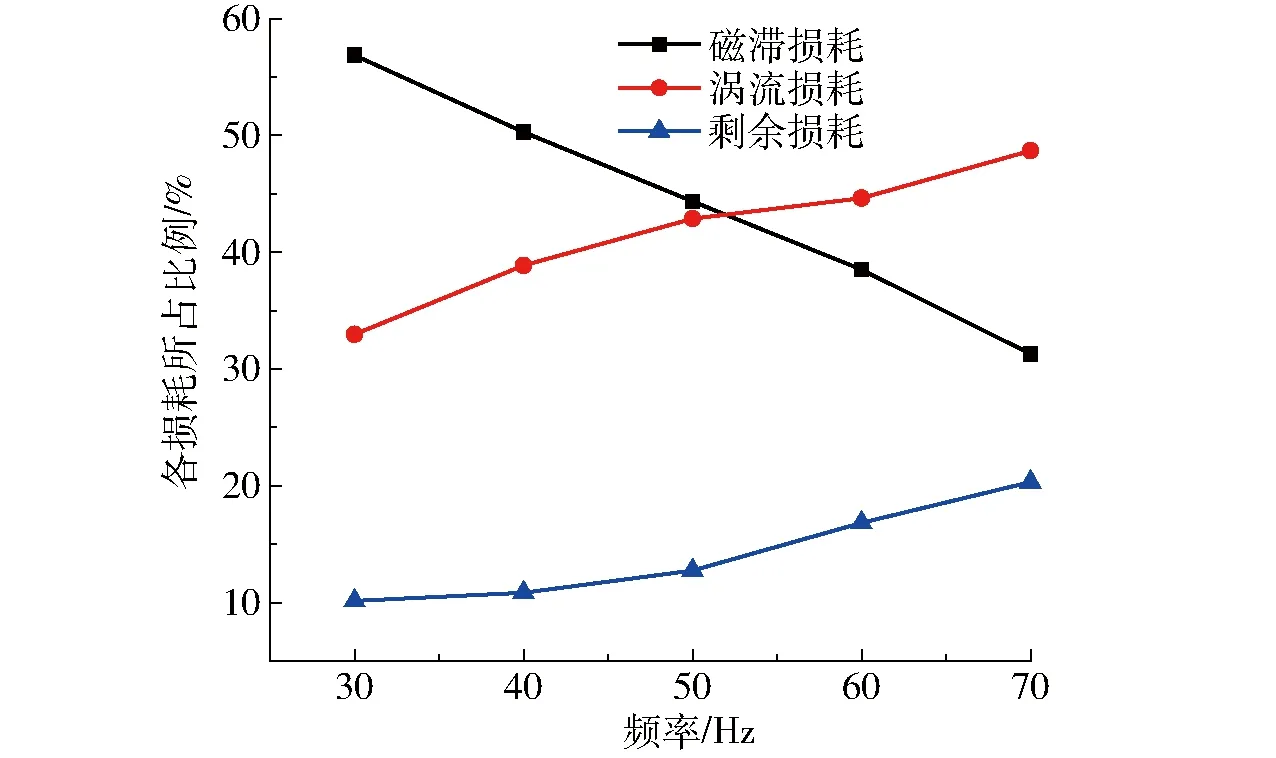
图12 不同频率下各损耗所占比例Fig.12 Proportion of loss under different frequencies

由式(14)可知，对于铁镓换能器而言，在高频磁场工作条件下，为了减少铁镓棒上的涡流损耗，可以对铁镓棒进行切片处理，而且铁镓棒的切片厚度越小，涡流截止频率越大，涡流损耗越小。将铁镓棒沿径向切成薄片，再将薄片进行粘接，通过增大铁镓棒的电阻，来减小铁镓棒上的涡流，进而减小了高频磁场下的涡流损耗，提高铁镓换能器的工作效率。

4 结论

(1)铁镓合金棒在相同磁感应强度下，随着磁场频率增加，动态磁滞回线面积增大，对应电磁损耗增大，矫顽力和剩磁增加。在相同磁场频率下，随着磁感应强度增加，动态磁滞回线为一系列同心椭圆，磁滞回线变宽变高，面积不断增大，电磁损耗增大，矫顽力和剩磁增加。

(2)在磁感应强度为1 725 mT时，磁场频率由30 Hz增至70 Hz，电磁损耗和介质储能分别增加了3.24倍和1.96倍，分离后的磁滞、涡流和剩余损耗分别增加了1.33倍、5.26倍和7.35倍。磁滞损耗所占比例由56.87%下降至31.31%，涡流损耗所占比例由32.98%上升至48.69%，剩余损耗所占比例略有上升。对于高频工作条件下的铁镓换能器，通过对铁镓棒切片处理，减小了涡流损耗，提高了铁镓换能器的工作效率。

1 翁玲, 赵青, 孙英,等. 考虑附加涡流损失的Galfenol合金动态滞后建模与实验[J/OL]. 农业机械学报, 2016, 47(4):399-405. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160452&flag=1&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2016.04.052.

WENG L, ZHAO Q, SUN Y, et al. Dynamic hysteresis model and experiment of Galfenol alloy considering excess eddy current losses [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(4):399-405. (in Chinese)

2 HUANG W, LI Y, WENG L, et al. Multifield coupling model with dynamic losses for giant magnetostrictive transducer[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4):1-5.

3 REDDY S M, PARK J J, NA S, et al. Electrochemical synthesis of magnetostrictive Fe-Ga/Cu multilayered nanowire arrays with tailored magnetic response[J]. Advanced Functional Materials, 2011, 21(24):4677-4683.

4 ATULASIMHA J, FLATAU A B. A review of magnetostrictive iron-gallium alloys [J]. Smart Materials & Structures, 2011, 20(4):4462-4473.

5 张艳丽, 何厚键, 谢德馨,等. 基于二维磁特性测量的电工钢片矢量磁滞模型[J]. 中国电机工程学报, 2010, 30(3):130-135.

ZHANG Yanli, HE Houjian, XIE Dexing, et al. Vector magnetic hysteresis model of electrical steel sheets based on two-dimensional magnetic property measurement[J]. Proceedings of the CSEE, 2010, 30(3):130-135.(in Chinese)

6 刘小军, 石玉, 赵宝林. 一种高频动态磁滞回线的PSpice电路模型研究[J]. 磁性材料及器件, 2011, 42(5):60-63.

LIU Xiaojun, SHI Yu, ZHAO Baolin. Study for a PSpice-based circuit model of high frequency dynamic hysteresis loop[J]. Journal of Magnetic Materials and Devices, 2011, 42(5):60-63.(in Chinese)

7 吴德会, 李雪松, 黄一民,等. 利用局部磁滞回线特性的无损检测新方法[J]. 仪器仪表学报, 2015, 36(10):2207-2214.

WU Dehui, LI Xuesong,HUANG Yimin,et al. New nondestructive test method with empirical research using local hysteretic loop characteristics[J]. Chinese Journal of Scientific Instrument, 2015, 36(10):2207-2214.(in Chinese)

8 张冬冬, 赵海森, 王义龙,等. 用于电机损耗精细化分析的分段变系数铁耗计算模型[J]. 电工技术学报, 2016, 31(15):16-24.

ZHANG Dongdong, ZHAO Haisen,WANG Yilong,et al. A piecewise variable coefficient model for precise analysis on iron losses of electrical machines[J]. Transactions of China Electrotechnical Society, 2016, 31(15):16-24.(in Chinese)

9 赵章荣, 隋晓梅, 邬义杰,等. 超磁致伸缩执行器全耦合非线性动态有限元模型[J]. 农业机械学报, 2008, 39(3):203-208.

ZHAO Zhangrong, SUI Xiaomei,WU Yijie,et al. Coupling nonlinear dynamic finite element model of giant magnetostrictive actuator[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(3):203-208.(in Chinese)

10 曹林, 何金良, 张波. 直流偏磁状态下电力变压器铁心动态磁滞损耗模型及验证[J]. 中国电机工程学报, 2008, 28(24):141-146.

CAO Lin, HE Jinliang, ZHANG Bo. Dynamic hysteresis loss model of power transformer under DC current biasing and its verification[J]. Proceedings of the CSEE, 2008, 28(24):141-146.(in Chinese)

11 曹永娟, 陶少卿, 余莉. 轴向磁场无铁芯永磁电机绕组涡流损耗分析与计算[J]. 东南大学学报:自然科学版, 2016, 46(6):1214-1220.

CAO Yongjuan, TAO Shaoqing, YU Li.Analysis and calculation of winding eddy current loss in stator-coreless axial-flux permanent magnet machine [J]. Journal of Southeast University: Natural Science Edition, 2016, 46(6):1214-1220.(in Chinese)

12 韩光泽, 朱小华. 介质中的电磁能量密度及其损耗[J]. 郑州大学学报:理学版, 2012, 44(3):81-86.

HAN Guangze, ZHU Xiaohua. Electromagnetic energy density and loss in medium[J]. Journal of Zhengzhou University:Natural Science Edition, 2012, 44(3):81-86.(in Chinese)

13 GYAWALI N, OHSAWA Y, YAMAMOTO O. Power management of double-fed induction generator-based wind power system with integrated smart energy storage having superconducting magnetic energy storage/fuel-cell/electrolyser[J]. IET Renewable Power Generation, 2011, 5(6):407-421.

14 NICOL H E, ROEHRDANZ H. Losses in three-phase induction machines fed by PWM converter[J]. IEEE Transactions on Energy Conversion, 2001, 16(3):228-233.

15 阙燚彬, 李涛涛, 谢溪凌,等. 叠堆结构对超磁致伸缩材料涡流损耗影响的研究[J]. 武汉理工大学学报, 2015, 37(9):100-105.

QUE Yibin, LI Taotao, XIE Xiling,et al.Study of the influence of stack structure on the giant magnetostrictive material eddy current losses[J]. Journal of Wuhan University of Technology, 2015, 37(9):100-105.(in Chinese)

16 马锃宏,李南,王汉斌,等. 温室株间电驱锄草机控制系统设计与试验[J/OL]. 农业机械学报,2015,46(1):89-93.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150113&flag=1&journal_id=jcsam. DOI:10.6041 /j.issn.1000-1298.2015.01.013.

MA Zenghong, LI Nan,WANG Hanbin, et al. Control system for electric drive intra-row weeding[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015,46(1):89-93. (in Chinese)

17 SIBILSKA-MRROZIEWICZ A, CZUBAJ S,ADYZYNSKA-KOZDRAS E, et al. The use of hall effect sensors in magnetic levitation systems[J]. Applied Mechanics & Materials, 2016, 817:271-278.

18 舒亮,李传,吴桂初,等. Fe-Ga 合金磁致伸缩力传感器磁化模型与特性分析[J/OL]. 农业机械学报,2015，46(5):344-349. http:∥www.j-csam.org/ch/reader/view_abstract.aspx?file_no=20150548&flag=1&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2015.05.048.

SHU Liang, LI Chuan,WU Guichu,et al. Magnetization model of Fe-Ga magnetostrictive force sensor and its characteristics[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015,46(5):344-349. (in Chinese)

19 USAK E, USAKOVA M. Analysis of microstructural changes in soft magnetic materials based on direct evaluation of magnetization process dynamics[J]. IEEE Transactions on Magnetics, 2014, 50(4):1-4.

20 陈萍, 唐任远, 佟文明,等. 高功率密度永磁同步电机永磁体涡流损耗分布规律及其影响[J]. 电工技术学报, 2015, 30(6):1-9.

CHEN Ping, TANG Renyuan,TONG Wenming,et al.Permanent magnet eddy current loss and its influence of high power density permanent magnet synchronous motor[J].Transactions of China Electrotechnical Society, 2015, 30(6):1-9.(in Chinese)

21 CHEN L, WANG J, NAIR S S. An analytical method for predicting 3-D eddy current loss in permanent magnet machines based on generalized image theory[J]. IEEE Transactions on Magnetics, 2015, 52(6):1-11.