基于引力搜索算法的植保无人机三维路径规划方法

王 宇 陈海涛 李海川

(东北农业大学工程学院， 哈尔滨 150030)

0 引言

将无人机作为载体，用于重复耗时的植保作业，可有效降低劳作压力与健康危害，而且植保无人机还具有作业高度低、药剂漂移少、对作物穿透性强等优势[1-3]。由于植保无人机药剂箱容量与电量的限制，在大田植保作业过程中，无人机往往需要多次返航进行药剂补充或电池更换，所以为了提高效率，须为其规划合理的返航点。目前植保无人机的作业方式主要有遥控作业和自主作业两种[4-5]。遥控作业通过飞手操纵完成，飞行路径与返航点安排也多是依赖飞手的经验。自主作业为无人机依靠其航点飞行与断点续喷等功能对田地自主进行喷施作业，其飞行路径须人为设置航点或田地边界。仅依靠飞手现场操纵与观察，并不能及时规划出较为理想的作业路径，同时，目前植保无人机的断点续喷功能并不支持对返航点的规划，这就会导致时间与能源的浪费。因此，为了使无人机的植保作业更加高效与节能，其路径规划已成为该方面相关研究中一个亟待解决的问题。

植保无人机的路径规划应与实际的农艺要求相结合，综合考虑作业过程中药剂补充与电池更换的问题，并对田地实现全覆盖[6-11]。针对植保无人机返航点的规划，徐博等[12]提出了一种以工作总耗能最小为目标的航迹规划算法，实现了田地的全覆盖路径规划与返航点位置的寻优。王宇等[13]提出了基于Grid-GSA算法的路径规划方法，能够针对具有不规则边界的田地区域规划出合理的返航点，使得非植保作业时间最短。但上述这些方法均未考虑三维地形的影响。

无人机在进行植保作业时，应以距离作物一定的高度飞行，以保证良好的喷施效果，目前大多数植保无人机通过加装超声波、双目、光流等传感器，也已经具备了定高飞行的功能；同时，由于有的田地存在高度起伏的情况，此时若将田地视为平面进行计算，则会导致计算得出的距离比实际飞行距离短，从而造成规划结果失真。所以对植保无人机进行路径规划时，应充分考虑飞行高度变化造成的附加飞行距离的影响。针对上述问题，本文运用引力搜索算法与三维栅格法，对一种可用于三维地形的植保无人机路径规划方法进行研究。

1 植保无人机三维路径规划方法

1.1 建立三维环境模型与路径仿真算法

根据实际的田地地理信息，运用栅格法(Grid method)将三维环境栅格化处理，建立环境模型，如图1所示[14]。栅格化后的三维环境模型，栅格边长为作业幅宽，另外每个栅格还包含栅格中心处的三维坐标(xi,yi,zi)与移动权值ωi等信息。其中，(xi,yi,zi)根据第i个栅格在田地中的实际位置与高度设定；初始栅格的移动权值ωi设为1或0，ωi=1的栅格为待作业区域栅格，ωi=0的栅格为不可进入栅格，如田地边界与田间障碍物等。

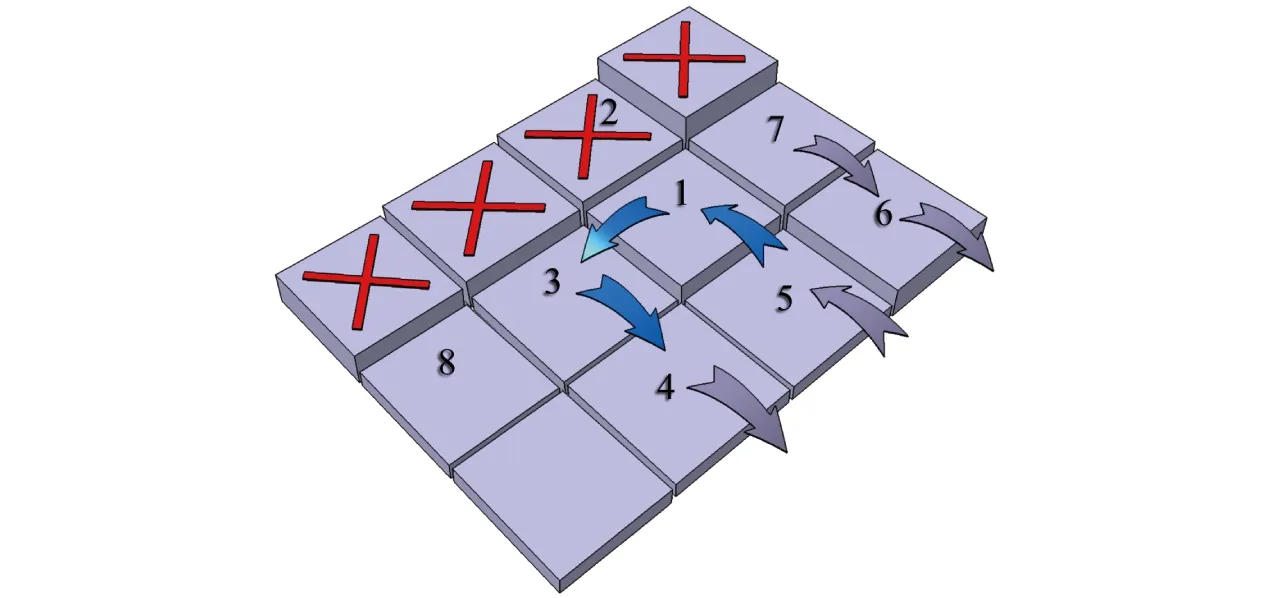
图1 栅格化三维环境模型Fig.1 3D grid environment model

在初始的栅格化环境中，设定无人机的初始时刻t0的位置(X(t0),Y(t0),Z(t0))位于栅格i，则无人机的初始位置为

(X(t0),Y(t0),Z(t0))=(xi,yi,zi+h)

(1)

式中h——无人机距离地面的高度

按照如下原则对无人机周围栅格的移动权值进行修正：

(1)若无人机前方栅格的移动权值不为0，则为该栅格附加移动权值奖励U1。

(2)若无人机左后方栅格的移动权值不为0，则为该栅格附加移动权值奖励U2，U2>U1。

(3)同步骤(2)，为无人机右后方栅格的移动权值附加奖励。

(4)将无人机后方栅格的移动权值置0。

按照该原则对无人机周围栅格的移动权值进行修正后，使无人机选择移动权值最大的栅格进行移动，且限制无人机仅能够向前、左、右3个方向移动，即可实现无人机往复全覆盖路径的仿真计算[8]。修正原则中，步骤(1)使无人机能够直行；步骤(2)、(3)使无人机能够在地头处回转；步骤(4)使无人机避免重复进入已作业区域。

如图1所示，为无人机在地头处回转飞行路径仿真。在t1时刻无人机由栅格5飞至栅格1，其前、后、左、右分别为栅格2、5、3、7。其前方栅格2为边界栅格，则ω2=0；栅格5、6、7为已作业区域栅格，由步骤(4)可知，无人机驶过的已作业区域栅格移动权值均为0，则ω5=ω6=ω7=0；由步骤(1)～(3)可知，移动权值为0的栅格不再接受奖励，故仅对无人机左后方栅格4进行移动权值修正，附加奖励U2，则ω4=1+U2；对于栅格3，没有相应的修正原则，所以其移动权值保持初始值不变，ω3=1。此时无人机可选择的3个移动方向中，左侧的栅格3移动权值最大，故在下一时刻t2无人机左转飞至栅格3。在t2时刻，按照前述原则对无人机周围栅格的移动权值进行修正，得出栅格8的移动权值ω8=1+U1<ω4，所以无人机下一时刻t3将左转飞至栅格4，从而实现在地头处回转。

1.2 建立基于引力搜索算法的返航点寻优模型

在1.1节路径仿真算法运算过程中，可设置无人机每次飞行距离的阈值D=(d1,d2, …,dN)，监测每次飞行的距离，当达到阈值时，记录无人机当前的位置Pn=(xn,yn,zn)，n=1, 2, …,N。由此可知，可根据载药量或电量设置飞行距离阈值D，从而得出返航点Pn，所以本文寻优模型以每次植保作业的飞行距离作为变量。

在同一栅格化的环境中，无人机植保作业时的总飞行距离不变，但由于返航点位置与数量的不同，会使得保障次数、返航点与补给点之间的总往返飞行距离也不同，所以要缩短总作业时间，则应减小总的往返飞行距离、药剂补充与电池更换次数等，若无人机飞行方向不受作物行方向的限制，则还须使得地头回转次数最小化，综上所述，建立目标函数为

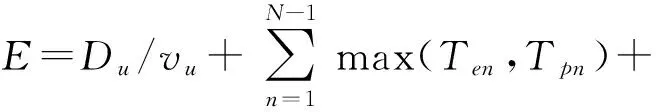
(2)

其中

P0=(x0,y0,z0)

式中E——总作业时间，s

Du——地头回转总距离,m

vu——地头回转飞行速度,m/s

Ten——第n次保障作业时更换电池时间,s

Tpn——第n次保障作业时补充药剂时间,s

P0——保障点的位置坐标

Hn——升降距离,m

voff——非植保作业状态下的飞行速度,m/s

本文运用引力搜索算法(Gravitational search algorithm，GSA)对寻优模型进行求解，其属于启发式算法，该类算法已经被广泛应用于诸多领域的路径规划问题并表现出较好的性能[15-20]。引力搜索算法的迭代规则为

(3)

(4)

(i=1,2,…,I;n=1,2,…,N)

式中ri——区间[0, 1]内的随机数

由于寻优模型中变量D=(d1,d2, …,dN)，其维数N在一次寻优中不能变化，但维数N对应返航点的数量，所以还须对不同维数分别进行寻优计算。

2 试验

试验中，植保无人机固有参数与田地地理信息为输入，返航点位置与数量为输出，设植保无人机电池容量可支持的续航时间为25 min，载药量所允许的最长植保作业时间为15 min，非植保作业状态下的直线飞行速度为6 m/s，地头的回转飞行速度为3 m/s，植保作业飞行速度为3 m/s，作业幅宽为5 m，电池更换时间Ten为1 min，最大药剂补充时间Tpmax为2 min，第n次药剂补充时间为

(5)

式中tb——基础药剂补充时间，设tb=20 s

Dn+1——第n+1次植保作业距离

Dmax——载药量所允许的最大植保作业距离

2.1 二维与三维区域返航点情况对比

建立如图2所示的三维环境模型，平面尺寸为700 m×100 m，边界形状不规则，作物行方向固定且已知，其二维平面图如图3所示，由矩形区域去掉左上角边长为100 m的等腰直角三角形，从而形成不规则边界，图2、3中坐标系均为非等比坐标系，保障点P0=(0, 0, 0)。

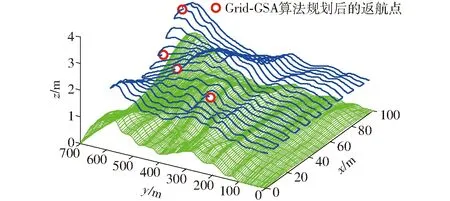
图2 三维地形返航点情况Fig.2 Return points in field with 3D terrain

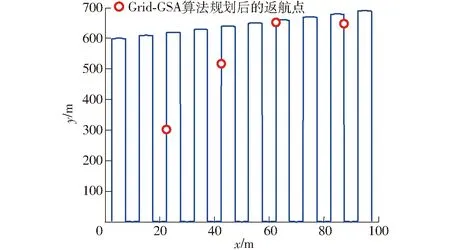
图3 二维地形返航点情况Fig.3 Return points in field with 2D terrain

未规划的返航点在三维与二维地形中的情况分别如图2与图3中的圆圈所示，具体数据如表1所示。

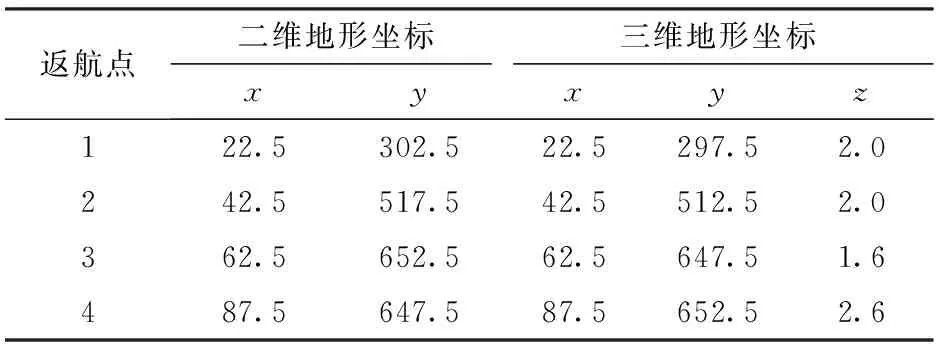
表1 二维与三维地形返航点情况对比Tab.1 Comparison of return points in fields with 2D and 3D terrains m

2.2 三维区域路径规划

建立与2.1节相同的三维环境模型，对返航点进行简单规划，即将返航点置于保障点所处的田地边界上，其具体位置的选取应在载药量所允许的范围内，运用仿真方法得出的简单规划结果如图4所示。

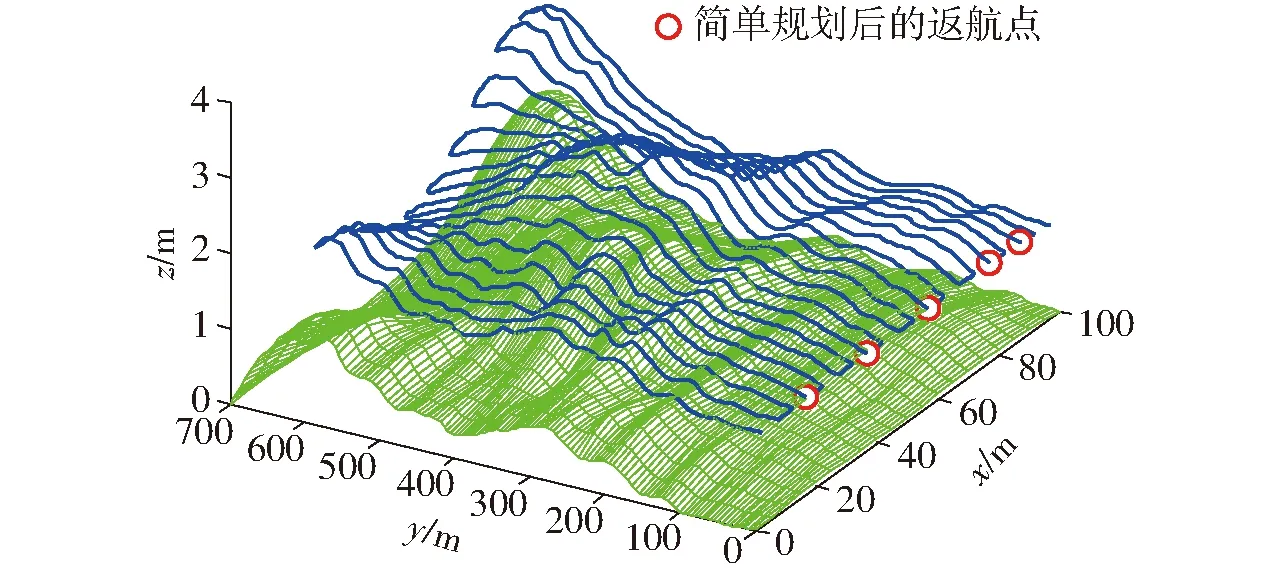
图4 三维地形简单规划情况Fig.4 Simple path planning for field with 3D terrain

运用本文提出的基于GSA算法的三维路径规划方法得出的变量结果为

D=(2 402, 2 484, 2 562, 2 669)

最终输出的实际植保作业距离为

D=(2 400.95,2 480.81,2 561.10,2 665.62,2 695.96)

具体的返航点数量与位置如图5所示。

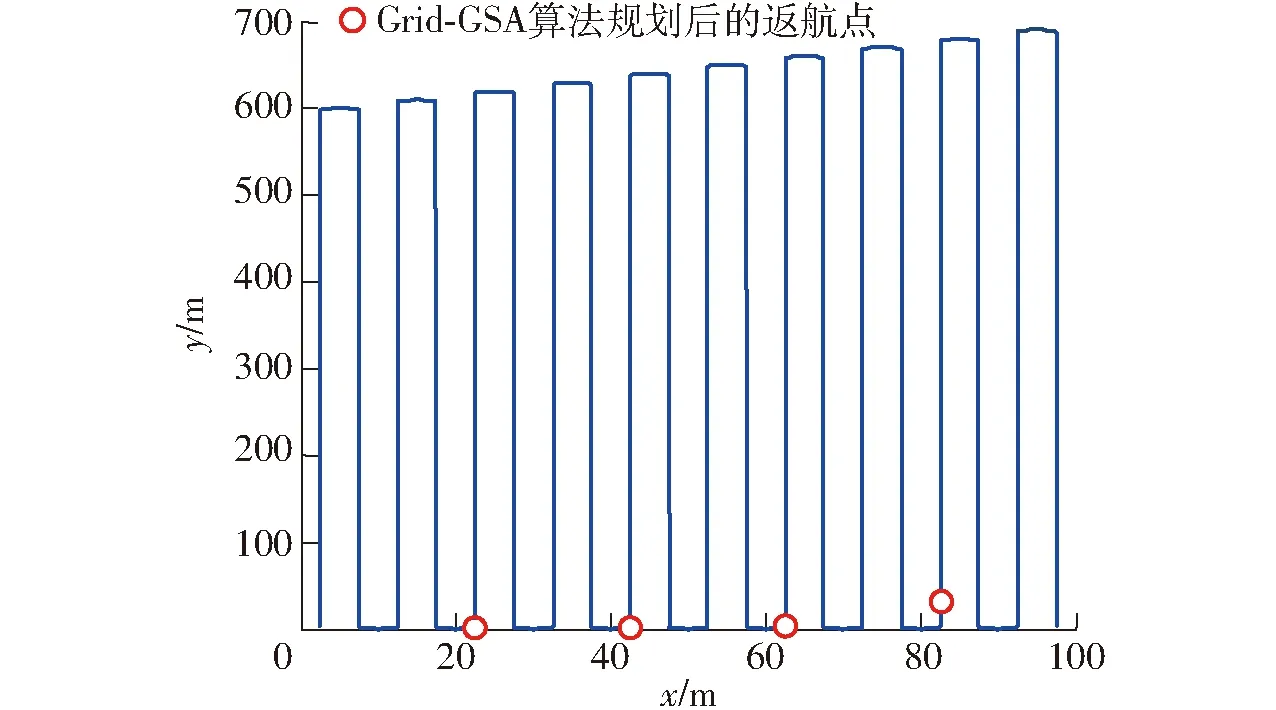
图5 基于GSA算法的三维路径规划结果Fig.5 Path planning results based on GSA

2种返航点情况及对应的相关数据信息如表2所示。

2.3 实际应用测试

使用作者自行设计制造的无人机作为试验机，无人机采用pixhawk开源飞行控制系统，具有图传与数传模块，采用GPS定位，使用气压计与超声波进行定高，具备航点飞行与地形跟踪功能，通过编程可模拟断点续喷功能，试验环境与试验机如图6所示。

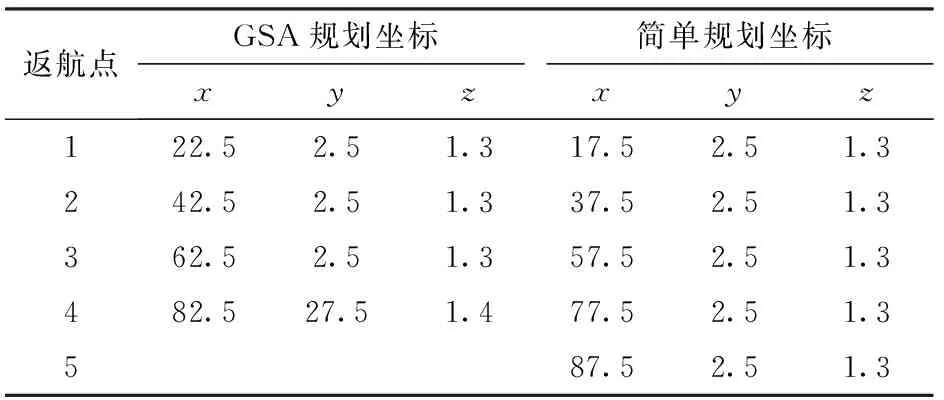
表2 不同规划方法计算的返航点情况对比Tab.2 Comparison of return points with different methods m

图6 试验机与试验环境Fig.6 UAV and environment for experiment

选取田地地形如图7所示(位于黑龙江省哈尔滨市宾县宣阳村，2017年5月11日)，田地具有不规则的边界，高度起伏2.9 m，无人机飞行高度1 m，等高线间距为0.5 m。

图7 试验田地Fig.7 Field for experiment

通过输入田地的实际地形数据信息，即可得出规划后的返航点，如图8所示。

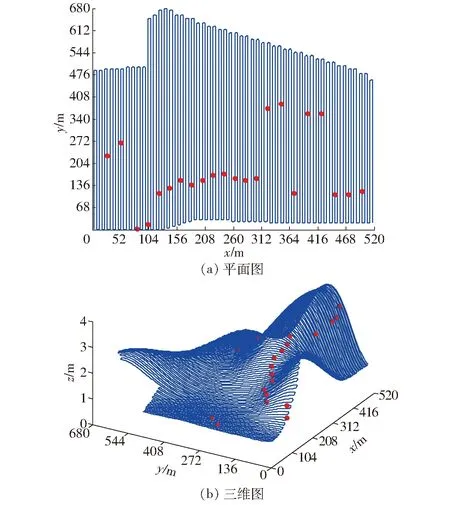
图8 试验田地规划后的返航点Fig.8 Optimal return points for experimental field

将计算得出的返航点输入地面站，使无人机按照设定航点飞行，根据数据传输模块传回的数据，得到规划前后的往返距离总和分别为16 387 m与14 578 m，非植保作业时间分别为85 min与81 min，规划后的各项数据情况如表3所示。

3 结果分析与讨论

对2.1节算例中的二维与三维田地进行路径规划时，生成的对应返航点之间存在偏差距离，这主要是由三维地形中额外的高度起伏对距离的影响造成的，表1中相对应的返航点之间的偏差距离为5 m，该距离的精度也与栅格划分的精细程度有关，本算例中由于栅格边长5 m，所以偏差距离的范围为0～10 m；在实际田地规划中，偏差距离范围为15～25 m。由于高度的起伏使得无人机的飞行距离增加，所以若不考虑三维地形的影响，就会造成药剂已经耗尽，而无人机仍继续作业的现象，从而导致药剂漏失，说明了本文研究的必要性。

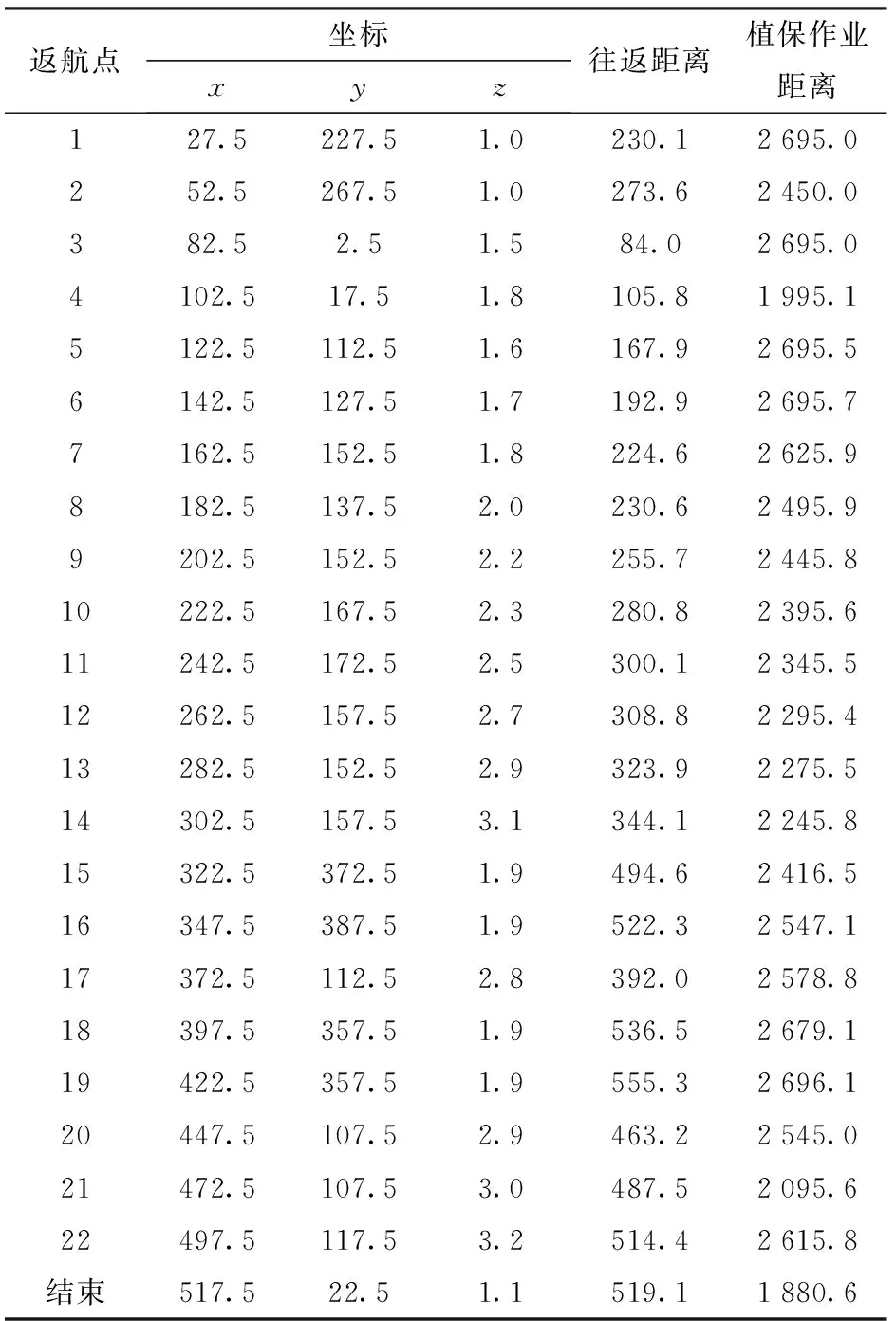
表3 试验田地路径规划数据Tab.3 Data of path planning result for experimental field m

在2.2节算例中，分别运用本文提出的基于GSA算法的路径规划方法与简单规划方法对返航点进行了规划，对比情况如表4所示。

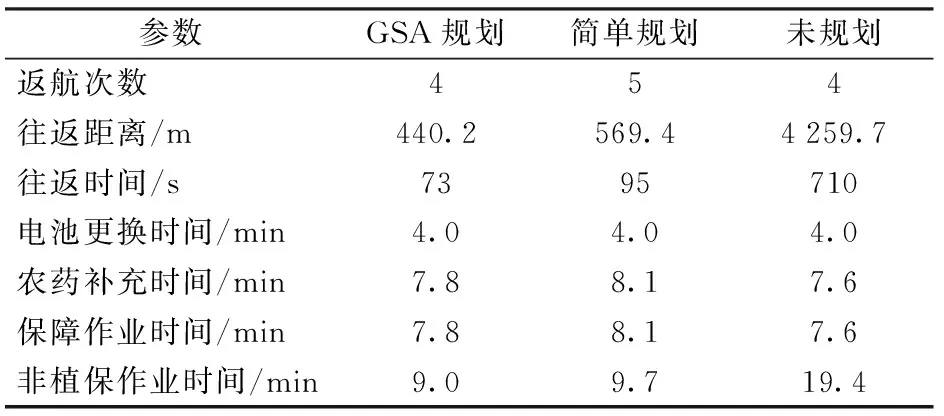
表4 路径规划结果数据对比情况Tab.4 Data comparison of path planning results

运用本文提出的基于GSA算法的路径规划方法规划后的结果中，往返飞行距离总和与非植保作业时间分别为440.2 m与9 min，相比于未规划情况分别减少了90%与54%，相比于简单规划结果分别减少了23%与7%。

3种方法得出的结果中，电池更换次数均为4次，药剂补充次数分别为4、5、4次。未规划情况下的保障作业时间最短，但由于往返距离较远，使得非植保作业时间最长。基于GSA算法的规划结果与简单规划结果相比较，往返飞行时间与保障作业时间均较短，2种方法的结果中，药剂补充平均时间分别为116 s与97 s，虽然后者优于前者，但由于药剂补充次数较多，所以增长了总的药剂补充时间。

根据续航时间与实际飞行时间计算并输出每组电池的电量消耗，如表5所示。3种方法的结果中，电池用量分别为5、6、5组。

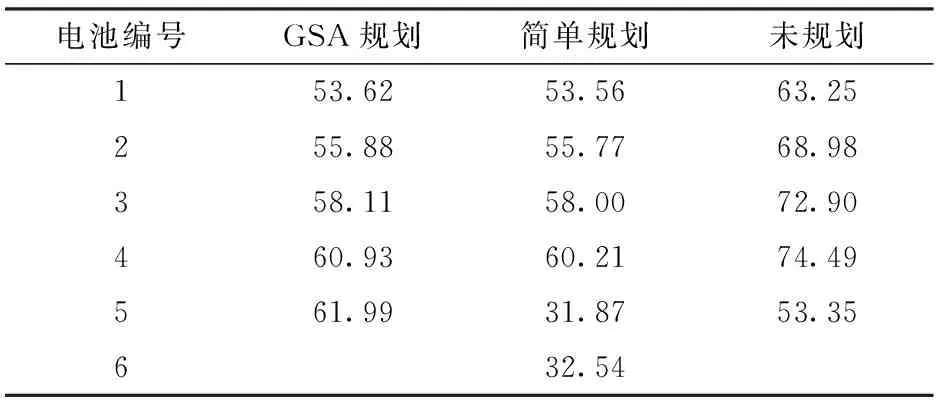
表5 电池使用情况Tab.5 Consumption of battery power %

在2.3节方法的实际运用过程中，规划前后情况对比，往返距离减少了11%，非植保作业时间减少了5%。由于目标函数中计算了垂直方向上的飞行距离，使得无人机往返路径尽量少的跨越较高的田地区域，具体规划前后的返航点分布与地形情况分别如图9、10所示。图9未规划的返航点中，有8个返航点位置，使得无人机在往返途中需要跨越较高区域，从而增加了垂直移动距离；而图10规划后的结果中，仅有5个返航点存在该情况。

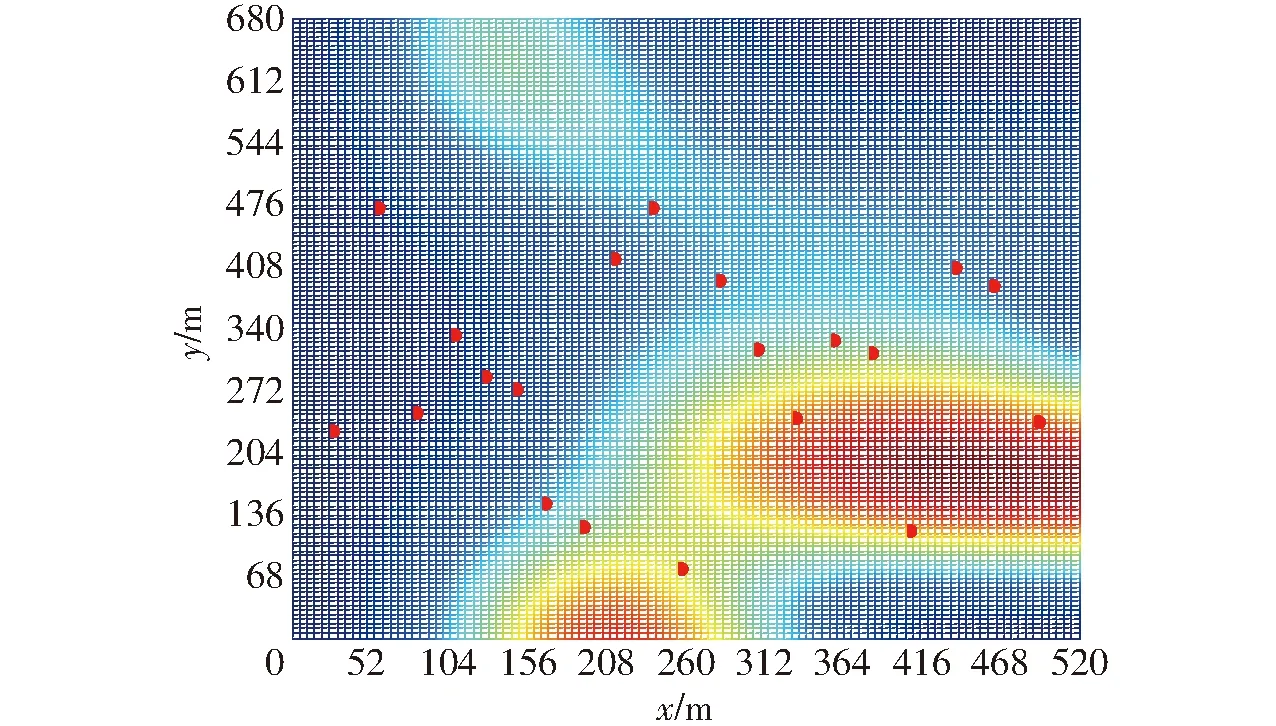
图9 试验田地未规划的返航点Fig.9 Unplanned return points in experimental field

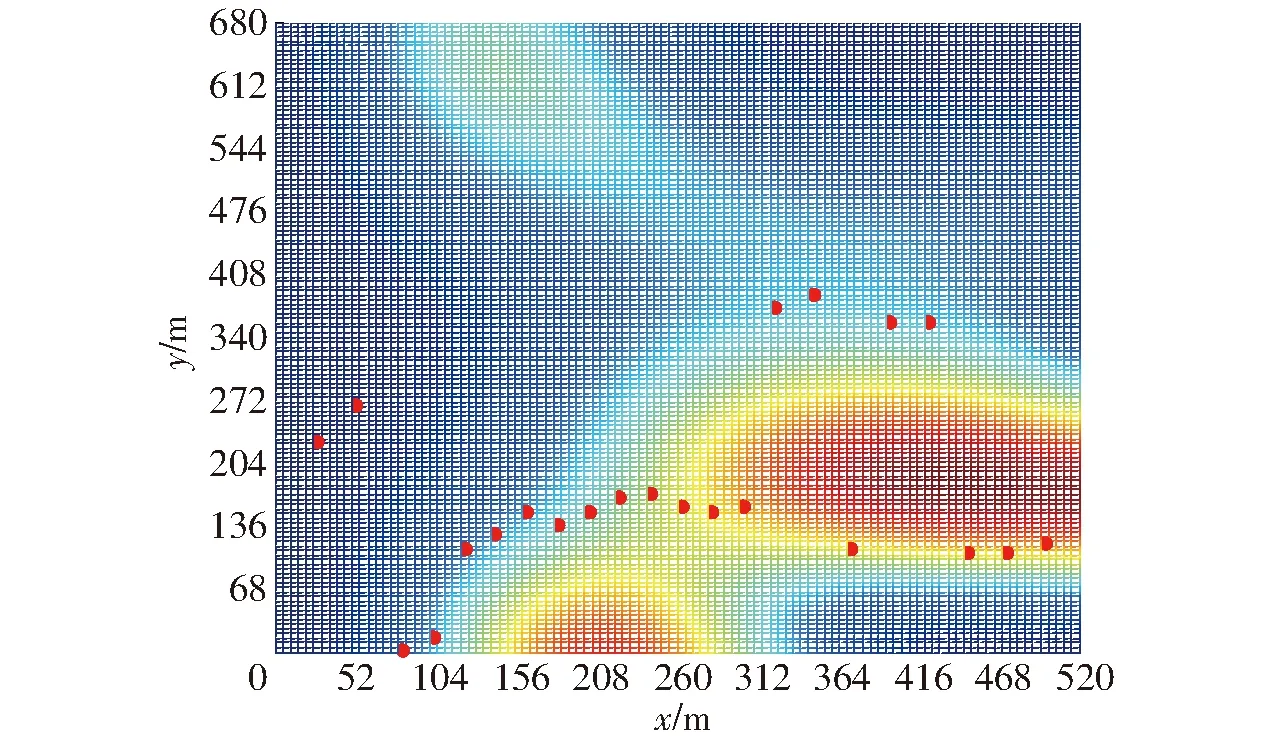
图10 试验田地规划后的返航点Fig.10 Optimal return points for experimental field

通过对算例与实际田地进行实际应用，对结果进行分析发现，方法能够适用于复杂情况的地理地形要求，搭建的模型能够按照目标函数进行寻优，考虑因素包含了保障作业时间、往返飞行的平面距离与垂直距离。

4 结论

(1)针对植保无人机的植保作业过程，提出了基于GSA算法的三维路径规划方法。通过对栅格化的环境模型附加高度信息，使得仿真算法中无人机的距离计算包含高度起伏变化引起的距离增加；建立的目标函数中也考虑了返航点与保障点之间地形的高度起伏引起的无人机起降距离的变化，从而增强了计算结果的可靠性。

(2)在实例检验中，运用本文提出方法得出的结果，相比于二维空间内的路径规划情况，返航点的位置存在偏差距离，说明了路径规划过程中考虑高度起伏的必要性。运用基于GSA算法的路径规划方法规划后，往返飞行距离总和与非植保作业时间分别为440.2 m与9 min，相比于未规划情况分别减少了90%与54%，相比于简单规划结果分别减少了23%与7%。在实际田地的路径规划应用中，田地形状与高度起伏情况更为复杂，本文提出方法不仅能够计算三维空间中返航点与保障点之间的距离，而且还综合考虑了返航途中由于高度起伏增加的距离，从而验证了该方法的合理性与可行性。

1 HUANG L, QU H, JI P, et al. A novel coordinated path planning method using k-degree smoothing for multi-UAVs[J]. Applied Soft Computing, 2016, 48: 182-192.

2 TISDALE J, KIM Z W, HEDRICK J K. Autonomous UAV path planning and estimation[J]. IEEE Robotics & Automation Magazine, 2009, 16(2): 35-42.

3 张东彦, 兰玉彬, 陈立平, 等. 中国农业航空施药技术研究进展与展望[J/OL]. 农业机械学报, 2014, 45(10): 53-59.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20141009&flag=1&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2014.10.009.

ZHANG Dongyan, LAN Yubin, CHEN Liping, et al. Current status and future trends of agricultural aerial spraying technology in China[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(10): 53-39.(in Chinese)

4 丁团结, 方威, 王锋. 无人机遥控驾驶关键技术研究与飞行品质分析[J]. 飞行力学, 2011, 29(2): 17-24.

DING Tuanjie, FANG Wei, WANG Feng. Development of UAV remote-piloted key technology and flight qualities[J]. Flight Dynamics, 2011, 29(2): 17-24.(in Chinese)

5 彭孝东, 张铁民, 李继宇, 等. 基于目视遥控的无人机直线飞行与航线作业试验[J/OL]. 农业机械学报, 2014, 45(11): 258-263. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20141140&flag=1&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2014.11.040.

PENG Xiaodong, ZHANG Tiemin, LI Jiyu, et al. Experiment of straight and airline flight operation for farmland based on UAV in visual remote mode[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(11): 258-263.(in Chinese)

6 YAO P, WANG H, SU Z. Cooperative path planning with applications to target tracking and obstacle avoidance for multi-UAVs[J]. Aerospace Science & Technology, 2016, 54: 10-22.

7 RAMANA M V, VARMA S A, KOTHARI M. Motion planning for a fixed-wing UAV in urban environments[J]. IFAC-Papers Online, 2016, 49(1): 419-424.

8 POPESCU D, STOICAN F, ICHIM L. Control and optimization of UAV trajectory for aerial coverage in photogrammetry applications[J]. Advances in Electrical and Computer Engineering, 2016, 16(3):99-106.

9 TORRES M, PELTA D A, VERDEGAY J L, et al. Coverage path planning with unmanned aerial vehicles for 3D terrain reconstruction[J]. Expert Systems with Applications, 2016, 55:441-451.

11 HAMEED I A, COUR-HARBO A L, OSEN O L. Side-to-side 3D coverage path planning approach for agricultural robots to minimize skip/overlap areas between swaths[J]. Robotics & Autonomous Systems, 2016, 76:36-45.

12 徐博, 陈立平, 谭彧, 等. 多架次作业植保无人机最小能耗航迹规划算法研究[J/OL]. 农业机械学报, 2015, 46(11): 36-42.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20151106&flag=1&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2015.11.006.

XU Bo, CHEN Liping, TAN Yu, et al. Path planning based on minimum energy consumption for plant protection UAVs in sorties[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(11): 36-42.(in Chinese)

13 王宇, 陈海涛, 李煜, 等. 基于Grid-GSA算法的植保无人机路径规划方法[J/OL]. 农业机械学报, 2017, 48(7):29-37.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20170704&flag=1.DOI: 10.6041/j.issn.1000-1298.2017.07.004.

WANG Yu, CHEN Haitao, LI Yu, et al. A path planning method based on Grid-GSA for plant protection UAV[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(7):29-37.(in Chinese)

14 GU J, CAO Q. Path planning for mobile robot in a 2.5 dimensional grid based map[J]. Industrial Robot, 2011, 38(3): 315-321.

15 王宇, 黄胜, 廖全蜜, 等. 基于引力搜索算法的船舶舱室布置方法[J]. 上海交通大学学报, 2016, 50(1): 131-139.

WANG Yu, HUANG Sheng, LIAO Quanmi, et al. A method for ship compartment layout design based on gravitational search algorithm[J]. Journal of Shanghai Jiao Tong University, 2016, 50(1): 131-139.(in Chinese)

16 王宇, 黄胜, 廖全蜜, 等. 基于引力搜索算法的舱室分布方案设计方法[J]. 哈尔滨工程大学学报,2016, 37(1): 48-52.

WANG Yu, HUANG Sheng, LIAO Quanmi, et al. Method for the layout design of ship cabins based on gravitational search algorithm[J]. Journal of Harbin Engineering University, 2016, 37(1): 48-52.(in Chinese)

17 MAC T T, COPOT C, TRAN D T, et al. Heuristic approaches in robot path planning: a survey[J]. Robotics & Autonomous Systems, 2016, 86: 13-28.

18 DAS P K, BEHERA H S, DAS S, et al. A hybrid improved PSO-DV algorithm for multi-robot path planning in a clutter environment[J]. Neurocomputing, 2016, 207: 735-753.

19 BEHNCK L P, DOERING D, PEREIRA C E, et al. A modified simulated annealing algorithm for SUAVs path planning[J]. IFAC-Papers Online, 2015, 48(10): 63-68.

20 RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA: a gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232-2248.