带下反桨尖旋翼气动噪声数值分析

曹亚雄，樊 枫

(中国直升机设计研究所 直升机旋翼动力学重点实验室，江西 景德镇 333001)

0 引言

早期的旋翼外形设计只考虑旋翼的气动性能，往往忽视噪声的影响。随着现代直升机技术的发展，直升机噪声尤其是旋翼的气动噪声问题越来越受到重视。旋翼的气动噪声问题十分复杂，不同飞行状态下的旋翼噪声成分也不同。其中，悬停、斜下降以及中速前飞等飞行状态下旋翼会不同程度地产生桨-涡干扰(BVI)噪声，一旦出现将会对周围环境及地面人员产生较大影响。研究表明，通过优化桨叶气动参数可以有效改善旋翼的噪声特性[1-3]。桨尖作为桨叶的主要气动参数之一，同时又是桨叶最为敏感的区域，其构型极大地影响着旋翼的气动性能和噪声特性。

桨尖形式包括后掠、尖削、前掠以及下反等。相对于后掠、尖削等桨尖二维平面形状，桨尖下反的研究开展较晚但发展迅速，已成功应用于国外型号。BERP(英国实验旋翼计划)旋翼[4-5]装配在“海王”、“灰背隼”和AW101等直升机上，取得了很好的实用效果。最新一代的BERPⅣ桨叶在BERPⅢ桨叶的基础上进行了优化，下反角从20°增加到25°，提升了悬停气动性能。日本的ATIC(通航直升机先进技术)项目[6-7]中的优化旋翼采用了下反桨尖，并改进了下反角，试验结果表明该旋翼的BVI噪声有所削弱。在国内，旋翼降噪设计方面，南京航空航天大学招启军[8-9]等吸取了曲线后掠桨尖和锯齿形桨尖等桨尖形状的设计思想，设计了一种变弦长，尖部尖削，具有非常规曲线前后掠形状的桨尖——CLOR桨尖，之后又对CLOR桨尖的气动性能进行了分析和优化，进而发展出CLORⅡ桨尖。桨尖外形对噪声的影响研究方面，西北工业大学[10]和中国直升机设计研究所[11]都开展了一些研究。目前，国内专门针对带下反桨尖旋翼的气动噪声计算研究还很少。

鉴于此，本文采用高精度的CFD/FW-H数值模型，针对带不同下反角度桨尖的旋翼气动噪声进行计算分析，重点分析了下反角为0°、20°和45°的三副旋翼近场噪声及地面噪声特性。

1 数值模拟方法

1.1 旋翼流场CFD计算模型

本文借助于先进的CFD方法[12]对旋翼流场进行数值模拟与分析，为噪声计算提供高精度的流场信息。采用惯性坐标系下的三维非定常雷诺平均N-S(RANS)方程进行求解，方程的具体形式可以表达为：

(1)

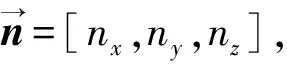
本文采用二阶MUSCL格式对单元内流场进行重构以获得网格交接面两侧的流场变量，并使用低耗散的ROE格式[13]计算网格交界面上的对流通量：

(2)

1.2 旋翼气动噪声计算模型

目前，旋翼气动噪声预测方法主要是基于FW-H方程和Kirchhoff方程的噪声分析方法。Kirchhoff方法能比较好地求解远场预测点总气动噪声，但Kirchhoff公式仅适用于线性区域，要求控制面能尽量地包含所有非线性不连续区域，具有较差的鲁棒性。FW-H方程物理意义明确，能比较好地计算旋翼厚度噪声和载荷噪声，而基于可穿透积分面的FW-H方程的提出，弥补了其计算四极子噪声的能力不足的缺陷，因此，基于FW-H方程的噪声分析方法正越来越成为预测噪声的主要手段。而Farassat 1A公式是FW-H方程的时域解，能应用于实际运动物体所致声场的计算。

本文直接给出Farassat 1A公式[14]：

(3)

(4)

(5)

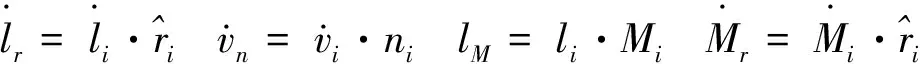
(6)

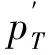
上述公式都是在延迟时间下进行计算，因此在噪声计算之前必须求得延迟时间。延迟时间τ计算公式可以表达为：

(7)

流场计算输出气动噪声计算所需的积分面处的压强等信息，噪声计算物理量的时间导数通过中心差分方法求解，延迟时刻的载荷通过插值得到。

1.3 模型算例验证

为检验本文的数值模型对直升机旋翼气动噪声的计算能力，选取了AH-1/OLS模型旋翼作为验证算例。美国学者Schmitz等人[15]测量了AH-1/OLS模型旋翼多个状态下的噪声数据，而这些噪声数据已被诸多学者作为其噪声计算方法的验证数据。选取“10014状态”进行噪声计算，此时桨盘倾角αTPP为1°，旋翼流场中存在明显的桨-涡干扰(BVI)现象，可以验证本文噪声方法计算桨-涡干扰噪声的能力。

从图1可以看出，本文方法在相位和幅值上均能较为准确地计算出AH-1/OLS旋翼在该状态下45°方位角左右的声压正峰值，这也正是桨-涡干扰状态的典型特征。作为旋翼空气动力学的一个研究重点，旋翼桨尖涡形成和运动的准确模拟至今仍比较困难，而本文方法能够分辨出该状态下的主要干扰点已属难得。因此，本文方法能够计算旋翼非定常桨-涡干扰状态的噪声，表明了本文方法具有计算旋翼桨-涡干扰状态气动性能和噪声特性的能力。

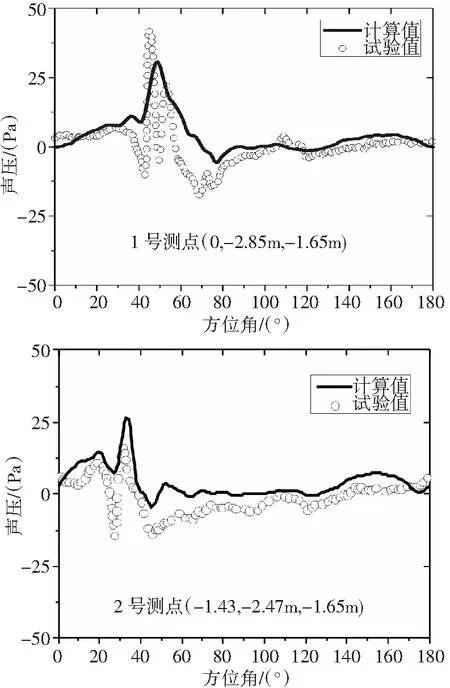
图1 AH-1G/OLS旋翼在典型桨-涡干扰状态下噪声对比

2 桨尖下反角度对旋翼悬停噪声的影响

针对桨尖下反构型，详细计算了不同下反角度对旋翼悬停噪声的影响，考虑到桨叶的结构设计和动力学影响，研究的桨尖下反角变化范围为0°～45°，旋翼外形为某型号旋翼的缩比模型，桨尖下反则从95%R处开始直线下反。观测点位置如图2所示。从图3(a)可以看出，观测位置#1和#2处的噪声总声压级随着桨尖下反角的增大而增大，这是因为#1和#2点均处于桨盘平面，该处的噪声以旋翼厚度噪声为主，而桨尖下反角增大(旋翼半径不变)将使得桨叶表面积增大，进而导致旋翼的厚度噪声增大，计算结果很准确地反映出了这一现象。此外，#3、#4、#5、#6号点处的噪声总声压级则随着桨尖下反角的增大而逐渐减小，其中桨尖下反45°时，旋翼噪声降低约1dB。需要指出的是，悬停状态下，桨尖马赫数约为0.6左右，旋翼载荷和压缩性较小，旋翼噪声本身不大，采用桨尖下反得到的噪声降幅实属难得，这表明桨尖下反角对降低旋翼噪声是行之有效的。从图3(b)可以看出，桨尖下反旋翼在高速状态下的降噪效果与低速状态下相近，表明桨尖下反对高速脉冲噪声影响不大。

图2 悬停观测点位置

图3 悬停状态下桨尖下反角度对旋翼噪声的影响

借助所建立的旋翼气动分析模型，分析桨尖下反降噪的气动机理，为了减少计算量，选取下反角0°、20°和45°三副旋翼进行对比分析。图4给出了不同桨尖下反角旋翼的涡流场情况，从图中可以看出，桨尖下反使得旋翼桨尖涡远离桨盘平面，同时，桨尖涡强度也有所减弱，这对降低直升机旋翼桨-涡噪声具有积极意义。

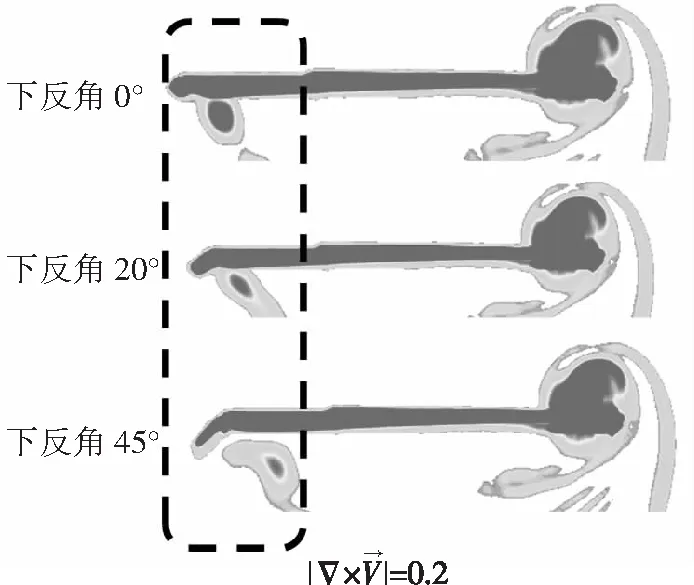
图4 不同桨尖下反角旋翼涡流场计算结果

3 桨尖下反角度对旋翼前飞噪声的影响

3.1 近场噪声

为进一步分析研究下反角度对前飞状态下旋翼气动噪声的影响规律，对桨尖下反角0°、20°、45°三副旋翼的气动噪声进行了计算。旋翼桨叶片数为5片，计算状态为直升机斜下降状态，即典型的桨-涡干扰状态：以-6°下滑角进行斜下降飞行，V=125km/h，Mtip=0.635。该飞行状态也接近于直升机噪声适航进场状态。

采用噪声辐射球弧面云图来表示旋翼近场噪声的大小和方向，球半径为4R，桨毂位于球心。图5给出了三副旋翼的噪声(单位：dB)辐射云图对比。从图中可以明显地看出，旋翼的前下方和前行侧下方噪声集中，噪声水平最高，表明这些区域出现了典型的桨-涡干扰，其气动噪声含有大量BVI噪声成分。另外，在噪声最大的区域里，桨尖下反20°和下反45°旋翼的噪声水平要明显低于无下反桨尖旋翼，而桨尖下反45°旋翼的降噪效果更加显著，这表明桨尖下反能够有效地降低旋翼的桨-涡干扰噪声。这是因为桨尖下反会使得桨尖涡在一定程度上远离桨盘平面，且桨尖涡强度也有所减小，这两方面原因均会减弱桨-涡干扰的强度，进而降低旋翼桨-涡干扰噪声。

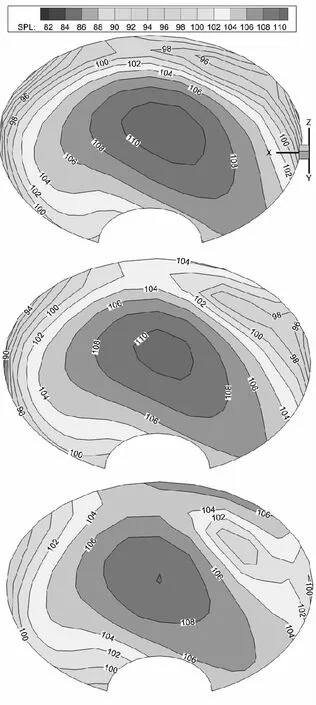
图5 三副旋翼的噪声辐射云图(从上到下依次为桨尖下反角0°、20°、45°)

进一步对旋翼前方噪声水平高的区域进行分析。图6给出了三副旋翼在该计算状态下的噪声差值云图。其中，纬线方向坐标为方位角，范围为90°～270°；经线方向坐标为噪声传播方向与桨盘平面夹角，范围为0°～70°。从图中可以看出，噪声降低区域集中在桨盘斜下方，尤其在前行侧最为明显，随着下反角度增加，降噪区域扩大到后行侧，噪声最大差值增加，并向下方移动，其中，噪声降低最大量约为4dB。在噪声差值最大的区域取点1和点2进行噪声时间历程的对比分析，如图7所示。图中给出了在一个旋转周期内，两点处声压值随方位角的变化对比，可以看出每片桨叶转过约75°发生强的桨-涡干扰，声压出现正峰值，在两次峰值之间有几个次峰值，是多个干扰点引起的桨-涡干扰现象。随着下反角增加，桨-涡干扰次数基本不变，声压正峰值明显降低，这表明带下反桨尖旋翼通过减弱桨-涡干扰强度来降低BVI噪声。

图6 三副旋翼的噪声差值对比

3.2 远场噪声

为研究桨尖下反旋翼对地面附近噪声的影响，计算了全尺寸旋翼的进场噪声。观测点阵列垂直于旋翼飞行方向，以飞行方向为中心线，布置在0m、+25m、+50m、+75m、+100m、+150m等侧向位置，共计11个。旋翼半径为6.75m，距离观测点的水平距离为120m，垂直距离为120m。图8给出了三副旋翼的噪声水平对比结果。从图中可以看出，在该飞行状态下，桨尖下反旋翼仍然能够有效地降低旋翼对地面的噪声影响，噪声最大降低量约1.5dB。

接下来，对旋翼大速度水平前飞状态下的噪声进行数值计算，计算状态为：以250km/h的速度进行水平飞行。该飞行状态接近于直升机噪声适航飞越状态。观测阵列距离桨毂中心的水平距离为120m，垂直距离为150m。图9给出了三副旋翼的飞越噪声对比，从图中看出无下反桨尖旋翼和桨尖下反20°旋翼的噪声水平基本相当，桨尖下反45°旋翼噪声最低，它在后行侧附近有一定降噪效果。

图7 #1和#2处声压值随方位角的变化

图8 不同侧向位置处测点处噪声对比

图9 水平前飞状态不同侧向位置处测点的噪声对比

4 结论

本文针对下反桨尖旋翼降噪特性开展了数值研究，通过对计算结果进行分析，获得了以下结论：

1)悬停状态下，桨尖下反对旋翼厚度噪声影响较小，但能够在一定程度上减弱载荷噪声，从而降低总的噪声水平。在正常悬停状态下，下反桨尖旋翼噪声降幅可达1dB。

2)前飞状态下，下反桨尖旋翼具有良好的降噪效果，通过减弱桨-涡干扰强度有效地减小BVI噪声。相对于无下反桨尖旋翼，下反45°桨尖旋翼的近场噪声在某些区域可降低4dB，远场地面噪声可降低约1.5dB。

3)仅从空气动力学的角度考虑，下反45°桨尖旋翼不论在悬停状态还是前飞状态下的降噪能力都更为显著。

[1] GOLUB R A, WEIR D S, TRACY M B．Application of the baseline ROTONET system to the prediction of helicopter tone noise[R]．AIAA-89-1135，1986.

[2] POLACSEK C，LAFON P．High-speed impulsive noise and aerodynamic results for rectangular and swept rotor blade tip tests in S1-Modane wind tunnel[C]．17th European Rotorcraft Forum, Berlin, 1991.

[3] PRIEUR J, LAFON P, CAPLOT M, et a1．Aerodynamics and acoustics of rectangular and swept rotor blade tips[J]．Journal of the American Helicopter Society, 1989, 34(1): 42-51.

[4] Robinson K, Brocklehurst A. BERPⅣ: aerodynamics, performance and flight envelope[C]. 34th European Rotorcraft Forum, 2008.

[5] Alan B, Earl P N D. Experimental and numerical study of the British Experimental Rotor Programme Blade[R]. AIAA-90-3008-CP.

[6] Hasegawa Y, Katayama N, Kobiki N, et al. Experimental and analytical results of whirl tower test of ATIC full scale rotor system[C]. 57th American Helicopter Society Annual Forum, 2001.

[7] Murashige A, Kobiki N, Tsuchihashi A. Second ATIC aeroacoustic model rotor test at DNW[C]. 26th European Rotorcraft Forum, 2000.

[8] 招启军, 徐国华. 新型桨尖旋翼悬停气动性能试验及数值研究. 航空学报[J]. 2009, 30(3):422-429.

[9] 王 博, 招启军, 樊枫, 赵国庆, 徐国华. 改进型CLOR桨尖旋翼悬停状态气动噪声特性试验与预估分析[J]. 空气动力学学报, 2013, 31(4):454-461.

[10] 宋文萍，韩忠华，王立群,等，旋翼桨尖几何形状对旋翼气动噪声影响的定量计算分析]J].计算物理，2001, 18(006)：569-572．

[11] 曹亚雄，樊 枫，林永峰等，先进桨尖旋翼悬停噪声计算与试验研究[C]．第三十一届中国直升机年会，2015．

[12] 樊 枫, 史勇杰, 徐国华, 剪刀式尾桨悬停状态气动力及噪声特性计算研究[J]. 航空学报, 2013, 34(9): 2100-2109.

[13] Roe P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.

[14] Farassat F, Succi G P. The prediction of helicopter rotor discrete frequency noise[J]. Vertica, 1983, 7(4): 309-320.

[15] Boxwell D A, Schmitz F H, Splettstoesser W R, el al. Model helicopter rotor high speed impulsive noise-measured acoustics and blade pressures[C]. The 9th European Rotorcraft Forum, 1983.