直升机主减速器行星齿轮系热分析

王正峰，夏富春，万 隆

(1.海军驻景德镇地区航空军事代表室，江西 景德镇 333001；2.中国直升机设计研究所，江西 景德镇 333001)

0 引言

直升机具有垂直起降、空中悬停性能和机动灵活的优点。传动系统作为直升机三大动部件之一，对直升机功能的实现和飞行安全起着至关重要的作用。齿轮结构是直升机传动系统的重要组成部分，其失效形式主要为齿面磨损、点蚀及胶合。本文主要以某型直升机减速器的行星轮系为例，从摩擦学角度出发，对齿轮在运转时由于摩擦因素而产生的磨损以及一系列后续问题进行研究，为齿轮的设计优化提供必要的参考。

1 轮齿啮合温度的分析

本文研究的某型机主减速器主要由两级行星轮系组成，结构如图1所示。

轮齿温度受影响因素很多，包括载荷、转速、齿轮的几何参数、齿面摩擦热流量的大小、齿轮端面和啮合面的对流传热系数、减速器空气温度和润滑油输入温度等。重庆大学龙慧的研究[1]指出，齿轮几何参数的改变,尤其是齿宽的大小,会对轮齿温度带来较大的影响；而模数改变导致的温度变化将取决于齿轮体积的改变、承载能力的变化以及对流传热系数的改变的综合结果。准确地测量减速器的空气温度和精确计算啮合面的摩擦热流量是保证有限元轮齿本体温度分析精确性的必要手段。

图1 某型机主减速器结构图

1.1 对流换热系数计算

在齿轮温度场分析计算中必须事先确定对流换热系数，齿轮换热系数主要取决于齿轮的冷却润滑方式及齿轮的运行条件。各散热表面的换热系数可大致分为两类：轮齿齿面的换热系数和轮齿端面的换热系数。

轮齿齿面的换热系数采取文献[2]提出的计算公式：

(1)

式中：K0为润滑油的导热系数；L为定型尺寸(取为齿轮分度圆直径d)；Pr为润滑油的普朗特数；Rε为雷诺数。

普朗特数为：

雷诺数为：

(2)

其中，ρf,cf,vf分别是润滑油的密度、比热和运动粘度；V为节圆上的线速度，hm为平均齿高。

轮齿端面的对流换热可以简化为旋转圆盘的对流换热情况来考虑，润滑油沿圆盘表面的流动可以分为层流和紊流。轮齿端面与润滑油之间的对流换热系数的确定如下：

层流状态：当雷诺数Rε≤2～2.5×105时，圆盘表面的流动属于层流：

(3)

紊流状态：当雷诺数Rε>2.5×105时，圆盘表面润滑油的流动变成紊流：

(4)

雷诺数Rε定义为:

(5)

式中：ω为圆盘的旋转速度；m为指数常数，用于定义圆盘表面温度沿径向的分布，这里取m=2；rc为圆盘表面上的任意半径。

1.2 摩擦系数的确定

啮合齿面的滑动摩擦被认为是齿轮系统功率损耗的重要来源，即是摩擦热产生的直接来源。Benedict等[3]提出的摩擦因数计算方法被广泛采用，齿面间的摩擦系数为：

(6)

式中：ωl为单位宽度上的载荷；η0为润滑油黏度；vs为啮合点处相对滑动速度的大小，vr为啮合点处卷汲速度的大小。

当齿轮在干运转运行状态的时候，由于失去了润滑油的减磨作用，齿轮间的摩擦系数增大，平均摩擦系数在0.18左右[4]，本文选用0.16的干运转摩擦系数。

2 行星传动系统摩擦热有限元分析

2.1 行星传动系统有限元模型

齿轮在运转过程中产生的摩擦热会影响齿轮的寿命，所以分析齿轮在旋转过程中的温升是十分重要的。通过有限元热固耦合对第一级行星齿轮系进行分析可以得出摩擦热。齿轮参数如表1。

根据以上信息，在有限元分析软件ABAQUS里建立齿轮的有限元模型。

2.2 干运转状态下齿轮对流换热系数的确定

2.2.1 轮齿啮合面对流换热系数

在忽略辐射散热的条件下，与周围热空气的对流换热成为干运转状态下齿轮散热的唯一方式。本文采用数值法进行对流换热系数的求解。在干运转条件下，减速器内的对流换热介质为热空气，根据式(1)来确定空气与齿面的对流换热系数。由于空气在减速器内部的流通性不强，随着摩擦热的增大，空气本身的温度也会上升，因此有必要考虑空气温升引起的对流换热系数的变化。下面列出了空气参数随温度变化的关系式[5]。

Pr(T)=0.707-2×10-4T

(7)

vf(T)=

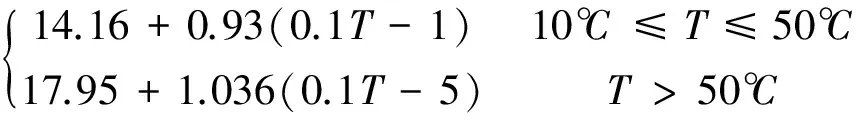
(8)

Ko(T)=2.43×10-2+8×10-5T

(9)

空气在不同温度下的热物性参数见表2。

表1 第一级行星齿轮系参数及载荷

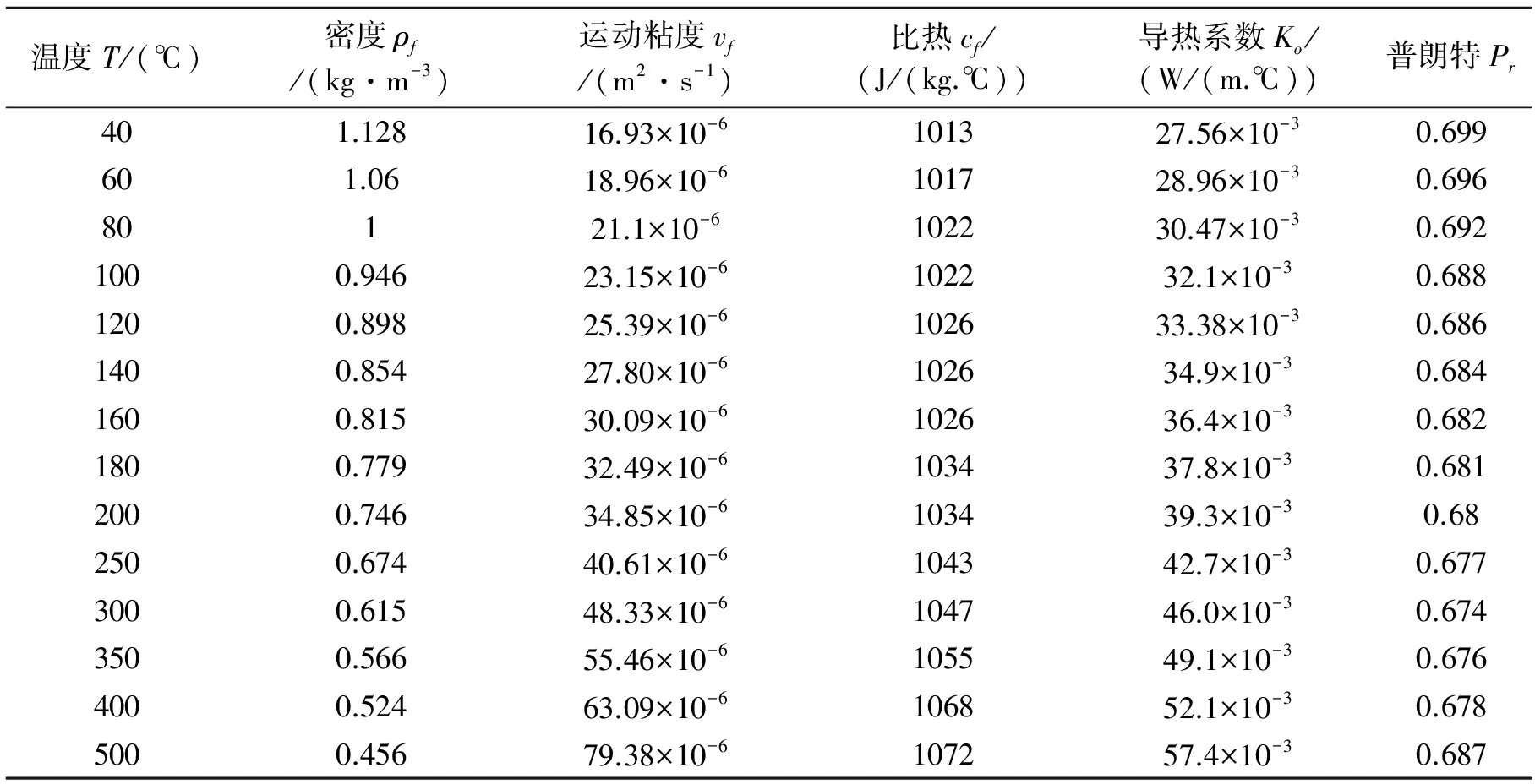
表2 空气在不同温度下的热物性参数

根据以上经验公式及热物性参数，在MATLAB下编程分别针对不同温度下各齿轮在干运转状态下啮合面上的对流换热系数进行了计算，以第一级行星齿轮系统的太阳轮为例，其轮齿啮合面对流换热系数如图2所示。

可以看出，在轮齿啮合面上，对流换热系数随温度升高而减小，可以预见随着干运转时间的增长，齿轮温升越来越高，散热却越来越少，达到一定程度后齿轮迅速失效。

2.2.2 轮齿端面对流换热系数

经过计算可知，第一级行星齿轮在干运转状态下高速运转时，其端面空气为层流流动状态，根据公式(3)和表2来确定空气与端面换热系数，在MATLAB下编程得到数据如图3所示。

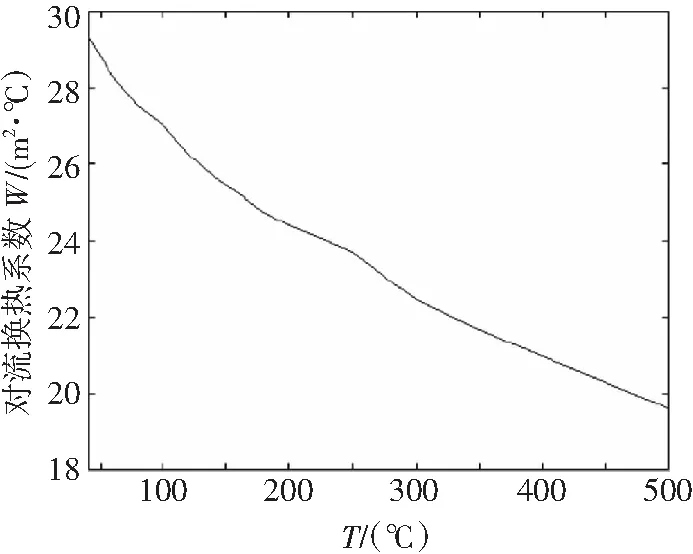
图2 轮齿啮合面对流换热系数

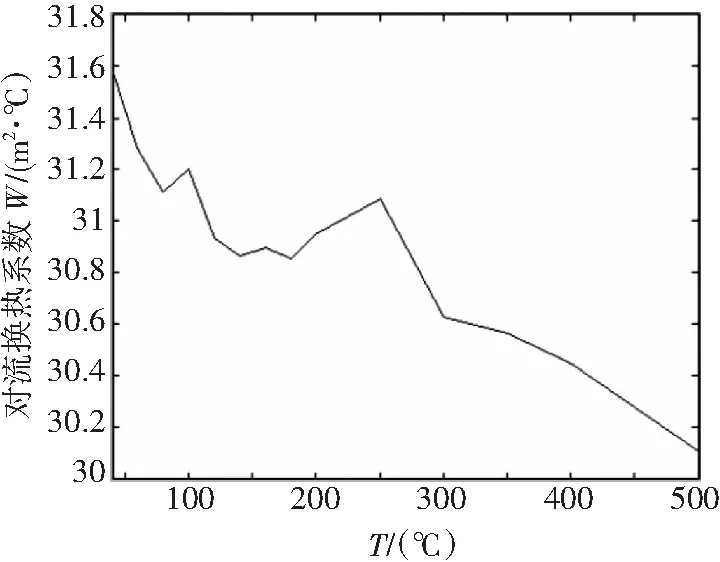
图3 轮齿端面对流换热系数

2.2.3 轮齿其他面对流换热系数

齿根、齿顶及非啮合齿面的对流换热系数可以近似按αt=(0.333～0.5)αs计算[6]，其余各面对流换热系数很小，可以将其作为零处理。

2.3 干运转状态下摩擦生热的计算

在高速干运转条件下，齿面间的相对滑动是齿轮摩擦热的最主要来源。齿面上由摩擦产生的热能可以初步认为全部传导进入齿轮。以下是模拟齿轮在无润滑散热环境下的温升，可以看出齿轮在没有润滑油进行散热的情况下会迅速失效，如图4所示。

图4简要表达了齿轮温升的过程，分别选取的是60s、270s、350s的图，可以看出随着时间的延长，齿轮高速运动产生很大的热量。其中太阳轮的发热量最大，最先损坏的也是太阳轮，太阳轮处需要有很好的散热条件来确保其稳定性。图5反映了齿轮温度上升的过程。

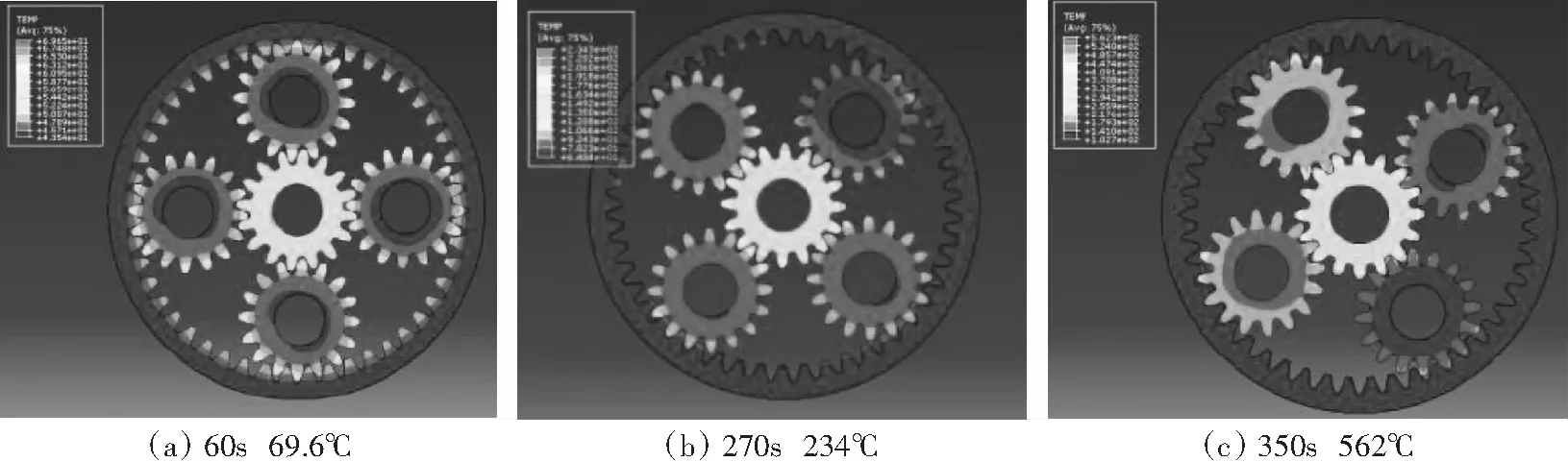
图4 无润滑条件下的摩擦温升过程

2.4 干运转条件下齿轮失效时间分析

在整个干运转过程中，随着时间延长，齿面润滑条件急剧恶化，此时最易发生齿面胶合的失效形式。一般淬火齿轮的胶合临界温度值取为220℃[7]。得到胶合附近的温升图如图6所示。

从齿轮的温升曲线可以看出，第一级太阳齿轮在265s的时候最高温度已经上升到222℃，已经到了齿轮的胶合临界温度，此时齿轮将会发生失效。

通过一定的优化设计方法降低齿面的摩擦系数，摩擦系数减小到0.06左右，能够在高温下一段时间内维持摩擦系数不变。以第一级行星齿轮为例进行优化处理，通过分析得到结果如图7所示。

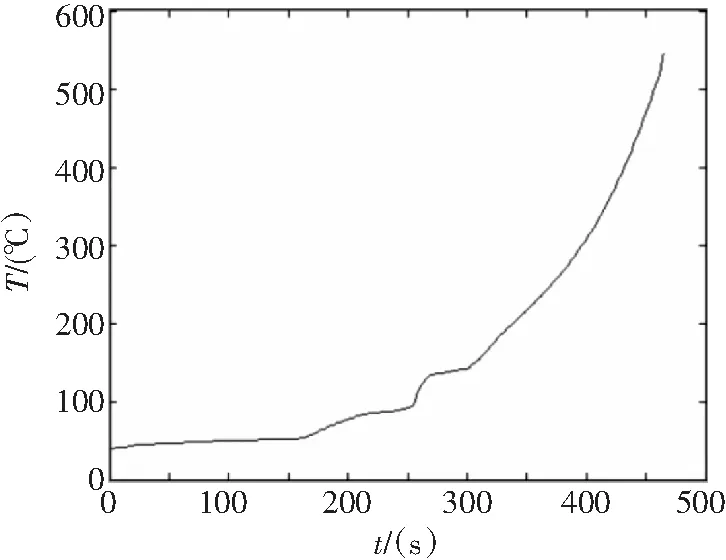
图7 最高温度变化趋势图(摩擦系数0.06)

在摩擦系数从0.16减小到0.06时，温升减小60%左右，从减小摩擦系数的角度来进行齿轮的优化设计对提高减速器的干运转能力有较大帮助。随着散热条件的变化，行星齿轮的温升也会相应地变化，分别在润滑油和空气作用的条件下对行星齿轮的温升进行有限元分析，如图8所示。

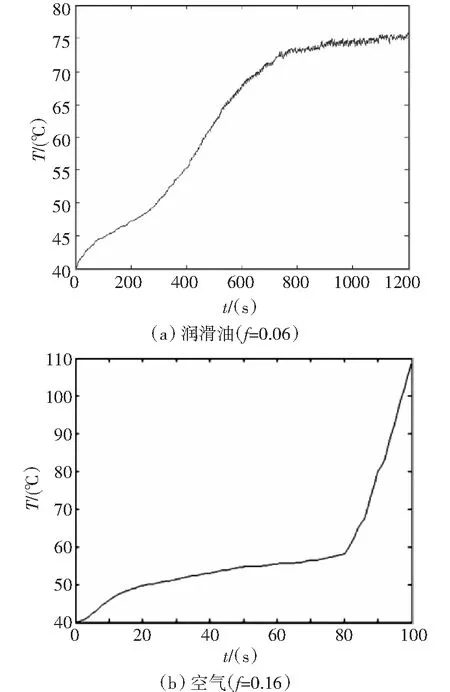
图8 行星齿轮在不同散热介质中的温升

在润滑油中的齿轮温度上升速率要小于在空气中的温度上升速率，700s后润滑油中的温度上升曲线逐渐趋于平缓状态，而空气中的温升曲线仍然很陡。因此，从改善主减速器润滑系统的角度来进行优化设计对提高主减速器的干运转能力有较大帮助。

3 结论

通过本文分析可知，提高齿轮的干运转能力，重点可以从改善主减速器的润滑系统和降低齿轮间摩擦系数等角度进行优化设计。具体建议如下：

1)表面技术：包括表面涂层技术和表面改性技术，使摩擦副在无油润滑条件下仍然具有低摩擦系数和足够的抗磨损能力。

2)耐高温材料和耐高温设计：耐高温材料在较高温度下，强度和硬度变化不大；耐高温设计，如增加齿侧间隙和轴承间隙等，能防止传动系统在干运转条件下由于热膨胀等导致运动干涉。

3)进行主减速器的温度场分布及散热方式的优化设计，提高散热效率。

4)提高齿轮的精度，降低粗糙度，降低摩擦系数。

[1] 龙 慧.高速齿轮传动轮齿的温度模拟及过程参数的敏感性分析[D]. 重庆：重庆大学,2001.

[2] 李绍彬.高速重载齿轮传动热弹变形及非线性耦合动力学研究[D].重庆：重庆大学,2003.

[3] Benedict G H, Kelley B W. Instantaneous Coefficients of Gear Tooth Friction[J]. Tribol. Tribol. Trans. 1961,4(1):59-70.

[4] 戴振东,廖自灿,刘贵龄,等.直升机传动系统干运转能力的研究[J] ,机械科学与技术,1999,18 (1):255-258.

[5] Mansion H. Some Factors Affecting Gear Scuffing [J], Inst. Petroleum, Jr.,1952,38(2):21-22.

[6] 苏 华,张永红,陈国定,等.弧齿锥齿轮热摩擦学行为研究的几个方面[J]，机械可与技术,2000(19):130-132.

[7] 温诗铸 ,黄 平.摩擦学原理(第3版)[M].北京：清华大学出版社，2008.