直升机金属结构缺陷深度统计分析

高 雅，喻溅鉴

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

金属结构在制造、加工、运输、装配、使用过程中难免会产生一些缺陷。由于检测手段或经济原因，这些结构部件会带着缺陷继续使用，缺陷对结构疲劳性能的影响不容忽视。缺陷的类型、尺寸、位置都会影响疲劳强度[1,7]。在金属结构的缺陷容限验证过程中,首先要根据制造、使用情况选择缺陷的参数，定义标准缺陷尺寸，然后确定合理的检查周期。标准缺陷尺寸的大小影响到检查周期的确定，过大则会使检查周期太小，过小则使需要的维修缺陷太多。对缺陷尺寸参数进行统计分析是缺陷容限设计必不可少的环节。

空直的强度验证文献中给出了缺陷类型和尺寸标准，其中提到缺陷尺寸标准是根据统计结果得出的[2]。国内方面，张永华[5]等从物理意义和数理统计两方面对水利水电工程中焊接接头缺陷的尺寸进行了概率分布模型的研究。陈勃[6]等认为试样上初始缺陷尺寸服从三参数Weibull分布，但是统计数量较少。而对国内直升机金属结构表面缺陷尺寸的统计未见相关研究。

目前在工程实际中主要参考国外的缺陷尺寸标准，而实际使用的材料和元件的加工工艺不同，缺陷的尺寸分布可能也有一定的差异。通过统计国内直升机金属关键件和重要件在制造加工、装配使用过程中发现的缺陷，得出国内直升机金属结构的缺陷尺寸实际分布情况，可以为缺陷尺寸标准的确定提供依据。

1 缺陷统计分析

缺陷尺寸统计的思路为：

1)收集和分类整理数据，画出频数分布直方图；

2)根据分布情况假设分布类型，并进行检验，确定分布类型和参数，即分布的概率密度函数；

3)根据得到的概率密度函数计算给定尺寸区间的缺陷数量的比例，或根据缺陷数量的比例确定尺寸范围。

1.1 数据来源

缺陷数据通过整理国内主要生产厂家大量生产过程中的缺陷记录获得。记录的信息主要有零部件名称、缺陷类型、尺寸、位置等。从中筛选出金属关键件和重要件的缺陷类型、尺寸和数量，分类整理。

1.2 分类整理和参数选择

金属结构的缺陷类型主要有划伤、冲击、腐蚀(图1)。本文中统计了划伤和冲击类型的缺陷，得到的参数主要有缺陷的长度、宽度、深度。缺陷底部半径也是影响疲劳性能的参数，此参数难以测量,记录中几乎没有缺陷底部半径的数据，所以无法统计。划伤的长度从几毫米到几百毫米不等，划伤长度与疲劳性能的关系不明显；宽度的数据量较少，难以系统地统计；所以统计时选择的尺寸参数是对疲劳性能影响显著的缺陷深度(以下提到的缺陷尺寸都是指深度)。

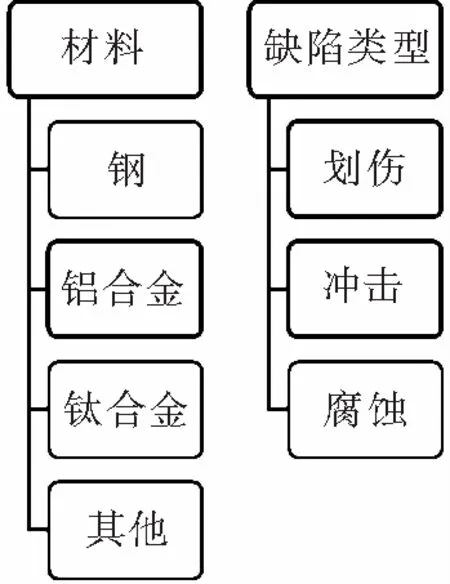
图1 缺陷分类整理

划伤主要由加工用的刀具或其他比较尖锐的物体沿平行于表面的方向造成，如图 2，主要包括划伤、擦伤、加工时的误铣、扎刀等。冲击多由垂直于表面方向的磕碰导致，形状通常表现为凹坑，如图 3。

收集到的缺陷尺寸常常是一个范围，如0～0.01mm。只有尺寸范围的原因可能是缺陷数量太多，尺寸相近；另一方面可能是缺陷尺寸太小，而且形状不规则，难以精确描述。在统计过程中，取尺寸范围的最大值。如0～0.01都取为0.01。

1.3 缺陷深度统计

1.3.1 关键件缺陷尺寸分布直方图

从收集的数据中选出关键件缺陷的尺寸和对应的数量，画出尺寸分布的直方图，如图 4。这些数据未区分缺陷的类型,包括划伤和冲击缺陷。

横轴上列出的是缺陷的尺寸，与实际收集整理得到的缺陷深度尺寸一一对应。

图4 金属关键件缺陷深度尺寸分布

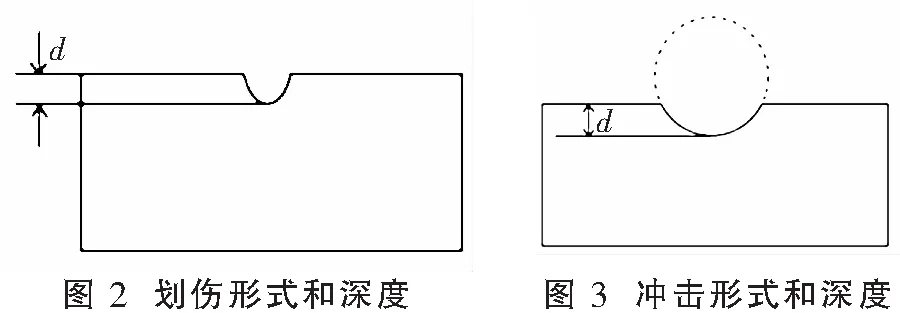
在尺寸较小时缺陷尺寸分布比较密集，而缺陷尺寸较大时分布比较稀疏。取深度d的对数lgd适当分组，得lgd的频数分布直方图，如图 5。直方图中间高，两头低，看起来样本像是来自正态总体。可以先假设缺陷深度尺寸服从对数正态分布。

图5 lg d的频数分布直方图

1.3.2 缺陷深度尺寸分布的检验

用χ2检验法检验lgd的分布，如果lgd服从正

态分布，则缺陷深度尺寸d服从对数正态分布[3]。

令X=lgd，

H0：X～N(μ，σ2)

(1)

先计算μ，σ的极大似然估计值，

(2)

(3)

分别计算X每个分组的理论频数n·pi和实际频数mi，计算结果如表 1。

样本数量n=260，分组数r=8，

(4)

未知参数有2个，μ和σ，未知参数个数k=2，

自由度为：

r-k-1=8-2-1=5

(5)

显著水平α=0.05，查表得：

(6)

所以接受H0，认为X服从正态分布。

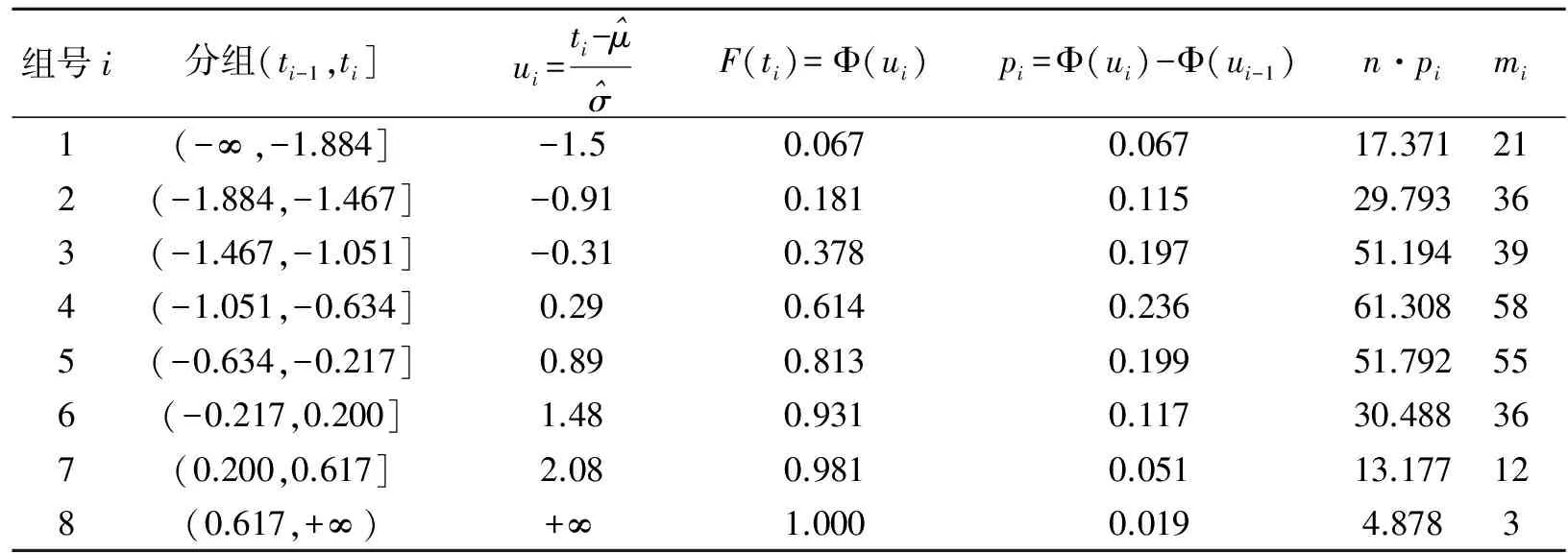
表1 检验计算表

拟合对比结果如图6。

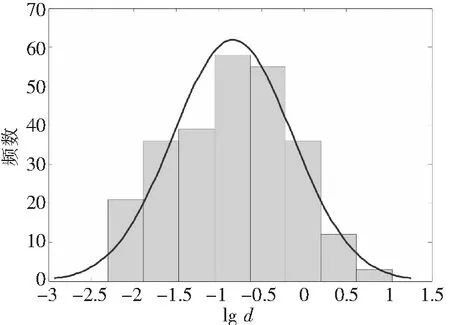
图6 关键件缺陷深度对数正态分布拟合

χ2拟合检验依赖于区间的划分，在检验中可能犯第Ⅱ类错误，分组不同时可能得到不同的检验结果。例如，改变分组数，可能出现图 7所示的情况。考虑同时用其他的检验方法来进行分布规律验证。用Jarque-Bera检验可以避免分组不同对检验的影响。[4]

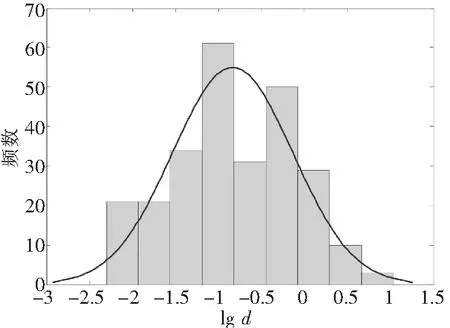
图7 改变分组数的一种情况

Jarque-Bera检验是一种常用的、基于峰度与偏度联合检验的正态性检验方法。检验过程大致如下：

H0:X～N(μ,σ2)

(7)

定义统计量：

(8)

其中KU表示峰度(kurtosis)，

(9)

SK表示偏度(skewness)，

(10)

其中：

(11)

正态分布的KU=3，SK=0。

对于给定的显著水平α，检验准则为：

(12)

使用MATLAB程序可以方便地用检验函数对数据进行Jarque-Bera检验。

读取、保存X数据之后，调用检验函数：

[h,p,stats,cv]=jbtest(x,alpha,tail)

(13)

其中，输入参数x为样本数据向量，alpha为检验的显著性水平(缺省时为0.05)，tail为备择假设类型的标示值，输出参数h为检验决策，p为拒绝原假设的最小显著性概率，stats为检验统计量的值，cv为拒绝域的临界值。

例如，使用 [J_h,J_p]=jbtest(data,0.05) 命令,得到结果：

J_h=0,J_p=0.0700

(14)

接受原假设H0，认为X在0.05显著水平下服从正态分布。

1.3.3 分布参数计算

以上缺陷尺寸对数的正态分布均值和方差通过极大似然估计计算得出。缺陷尺寸取对数后计算均值和方差，即为X的正态分布的均值和方差。由此得到正态分布的概率密度曲线。根据概率密度曲线可以计算给定尺寸区间的缺陷数量的比例，或根据缺陷数量的比例确定尺寸范围。

2 铝合金结构缺陷尺寸统计和参考标准

不同材料、不同缺陷类型，其深度的分布规律可能不同。使用同样的方法，可以区分不同材料、不同缺陷类型，分别对其深度进行统计和分析。

缺陷记录中铝合金结构上的缺陷数量较多，因此对铝合金结构的缺陷进行了详细统计。

2.1 铝合金划伤尺寸分布

图8为铝合金划伤深度尺寸分布的直方图，每一条与所有出现的划伤尺寸一一对应，纵坐标为对应的数量。

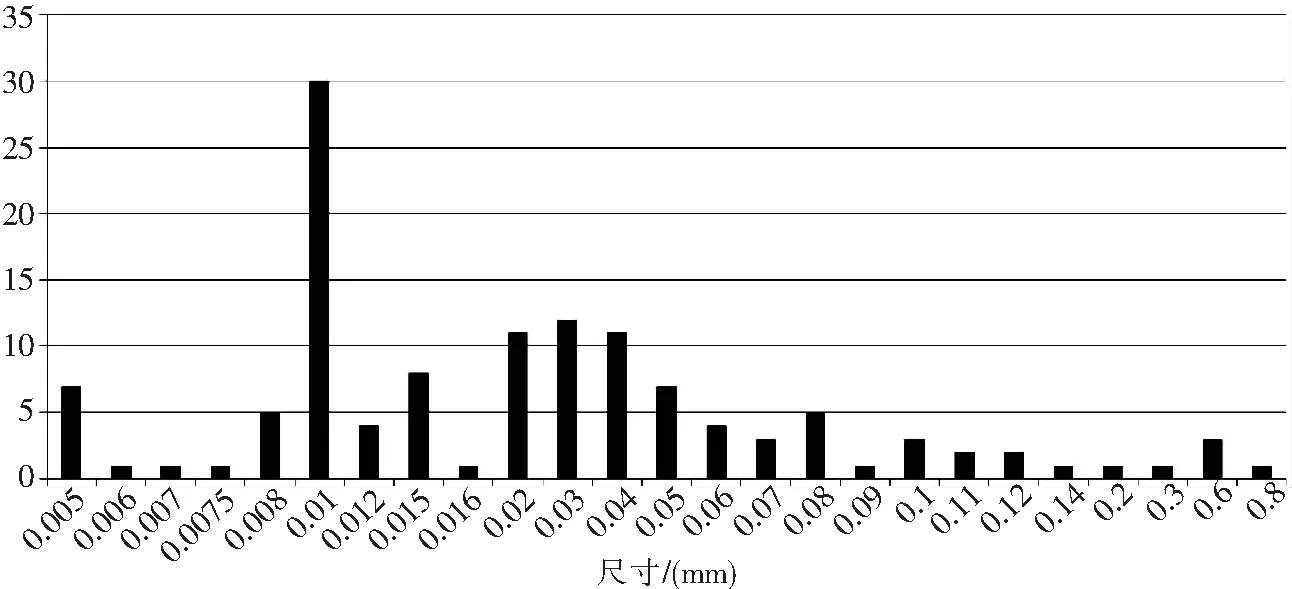
图8 铝合金划伤深度频数分布

由图可以明显看出0.01mm尺寸的缺陷最多，远多于其他的尺寸。0.01mm的划伤数量占总体比例30/126=0.238。

0.01mm的划伤数量偏多是因为收集到的数据很多是一个范围，如0～0.01，而分类、整理时都取为0.01mm，导致取整的那组数据数量明显多于前后几组。

除0.01mm组的数量偏多影响了分布的拟合外,如果不考虑0.01mm组的数据，其他缺陷尺寸分布符合正态分布，如图 9。

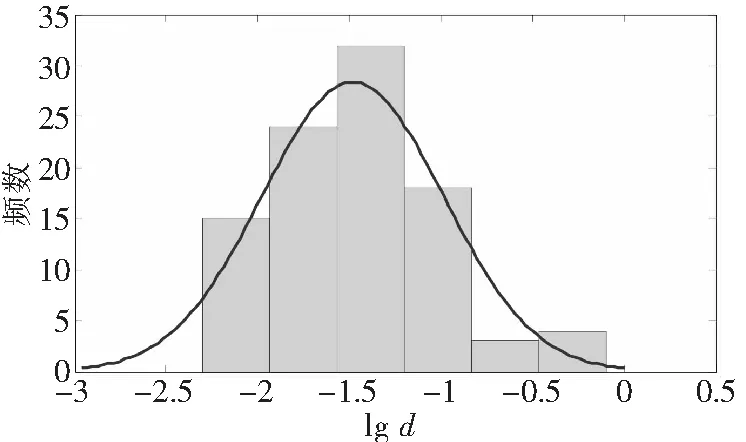
图9 铝合金划伤尺寸分布(不含0.01mm)

正态分布的参数：

μ=-1.481

(15)

σ=0.495

(16)

根据概率密度函数，求出一定比例对应的缺陷

尺寸，如表 2。考虑到测量精度水平和可操作性，取小数点后两位。

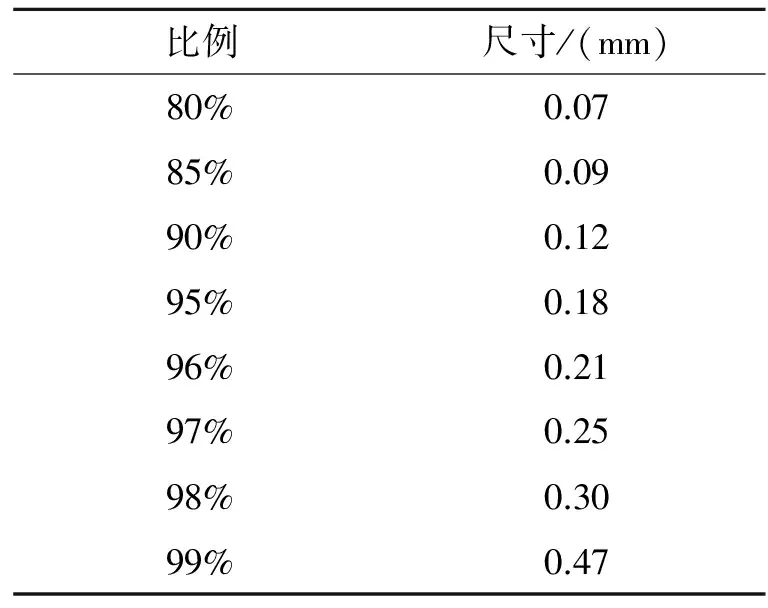
表2 铝合金划伤深度参考标准

2.2 铝合金冲击尺寸分布

图10为铝合金划伤深度尺寸分布的直方图。

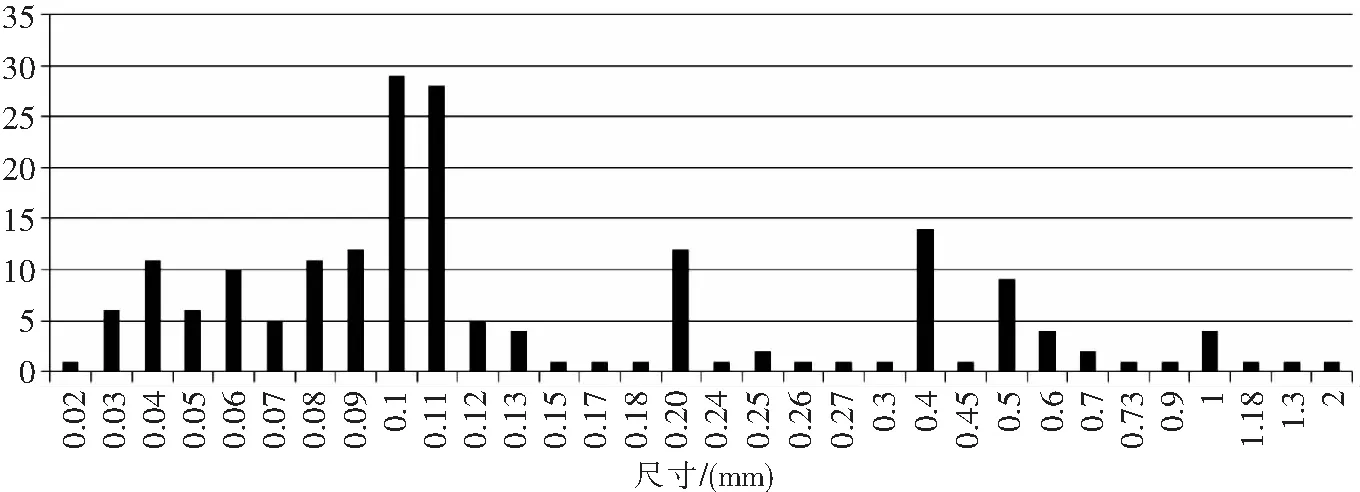
图10 铝合金冲击深度频数分布

对于铝合金冲击缺陷，没有明显的连续分布规律，冲击深度尺寸分布有两个峰值，分别在0.1mm和0.4mm附近。约90%的冲击缺陷在0.4mm以内。对应的百分比见表 3和图 11。

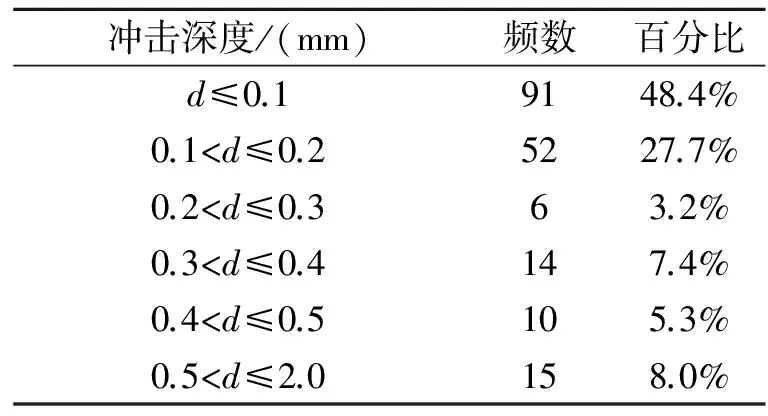
表3 铝合金冲击深度尺寸和比例

3 结论

金属关重件加工制造和装配使用缺陷深度尺寸服从对数正态分布。

对带缺陷结构的材料和缺陷类型进一步划分，获得铝合金划伤和冲击缺陷深度尺寸分布，对于铝合金，0.01mm的划伤尺寸最多，约占样本数量的23.8%，其他尺寸服从对数正态分布，可以根据分布规律选择适合的缺陷尺寸标准。

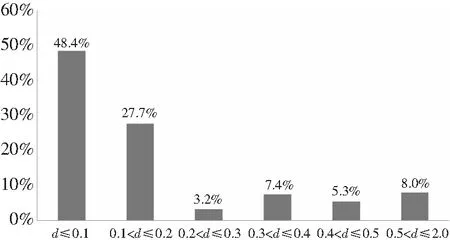
图11 铝合金冲击深度分布

冲击缺陷深度尺寸大致有两处峰值，对于铝合金，其峰值分别在0.1mm和0.4mm附近。

根据铝合金缺陷尺寸分布可以猜想其他种类金

属上的缺陷尺寸分布情况，比如钢的划伤和冲击缺陷尺寸分布类型可能与铝合金相同，具体分布和参数需要更多数据进行验证。

[1] 顾文标，喻溅鉴，邹 静，等.直升机金属结构缺陷容限验证技术研究[J].直升机技术,2013(1):20-25

[2] LAILLET E. General principles for static, fatigue and damage tolerance[R].EC technical report,2006

[3] 葛余博.概率论与数理统计[M].北京：清华大学出版社，2005.

[4] 包研科，李 娜.数理统计与MATLAB数据处理[M].沈阳：东北大学出版社，2008.

[5] 张永华，张天会，顾丽春，等.焊接接头缺陷尺寸概率分布模型研究[J]. 云南农业大学学报，2013(2)：264-269.

[6] 陈勃，刘建中，吴学仁，等.初始缺陷尺寸分布的尺寸效应研究[M]. 航空学报,2006(1):44-49.

[7] 《飞机设计手册》总编委员会，编．飞机设计手册第19册-直升机设计[M]．北京：航空工业出版社，2005．