基于EVA与经营风险偏好的供应链鲁棒优化模型

于丽萍,林丽凤,邱若臻

(东北大学工商管理学院，辽宁 沈阳 110169)

1 引言

创造股东价值通常被认为是企业最重要的商业目标[1]，实现股东价值创造需要进行相应的绩效与风险管理[2]。经济增加值(EVA)作为最重要的财务绩效指标能够使企业确定哪里创造了价值[3]。基于价值创造的供应链绩效管理的研究已经受到越来越多学者的关注。Christopher 和 Ryals[4]研究了供应链策略对股东价值创造的影响，Walters[5]、Lambert 和 Pohlen[6]讨论了供应链环境下价值管理的理论框架，提出了EVA导向的价值驱动树从而将供应链运作绩效与价值创造联系起来。Hahn 和Kuhn[7]将EVA作为供应链价值创造中期销售与运作计划的绩效指标，开发了优化EVA的确定性决策框架，并在计算EVA时通过调整资本成本间接地考虑了风险的影响。供应链风险管理则主要关注供应链中与物流相关的风险，如Pongsakdi等[8]利用风险曲线和平均近似取样的方法对提炼厂营运计划的风险管理进行了案例研究，You Fengq等[9]提出了关于化学供应链风险管理的两阶段随机规划方法，Goh et al[10]研究了供应链多阶段风险管理的框架，只有Sodhi 和Tang[11]提出的资产负债管理驱动的供应链风险管理方法同时考虑了与物流和资金流相关的风险。

鲁棒优化的方法可以通过考虑决策者的风险规避偏好采取不同的鲁棒标准进行风险管理[12]。Mulvey 和Zenios[13]比较系统的介绍了鲁棒优化的目的，特点应用领域等，并建立了鲁棒优化模型的的一般形式。Yu 和Li[14]以及Leung等[15]认为鲁棒优化方法可以应用于供应链的总体规划，Aghezzaf[16]研究了需求不确定时生产能力扩张与仓库选址的鲁棒优化问题，李春发等[17]在考虑风险偏好的情况下建立了需求不确定的动态生产库存鲁棒优化模型，并通过鲁棒优化理论得到预期的确定性鲁棒对应模型。但是这些研究没有综合考虑供应链的绩效与风险管理，并不是从价值创造的角度建立供应链的鲁棒优化模型。最近，Hahn 和Kuhn[18]采用下偏矩的方法来描述EVA的下行风险，建立了绩效与风险管理相结合的供应链鲁棒优化模型，但是只考虑了产品需求不确定对EVA的影响，却没有考虑决策者对经营风险的规避偏好态度对EVA的影响，也没有考虑资本成本不确定的相关风险及其对EVA的直接影响。

价值创造要取决于绩效模式与相应的经营风险[7]。EVA作为体现价值创造的绩效指标，是从税后净营业利润中扣除全部投入资本成本后的所得，其核心理念是资本成本。资本成本是企业筹集和使用资金付出的代价，现实中会随着债务的利率及股东所要求的报酬率变动而具有不确定性，给价值创造带来了与资金流相关的风险。经营风险源自于经营过程中未来事件(非自然或人为灾害)的不确定性[19]，其中产品需求的不确定是一个主要因素，而且由于经营杠杆作用的存在，需求的波动会导致营业收益更大的波动，从而直接影响到价值创造。因此，针对现有研究的不足，本文在Hahn与Kuhn[7]研究的基础上，同时考虑物流与资金流风险对EVA的影响，将需求与资本成本的波动描述成不同的情景；并考虑决策者对经营风险的规避偏好对EVA的影响，采用经营杠杆系数描述经营风险。通过鲁棒优化的方法将一个制造商和多个外部供应商构成的多产品、多阶段供应链的绩效与风险管理结合起来，建立供应链鲁棒优化模型，得到最优的鲁棒运作策略，实现价值创造的目标。

2 问题描述

为了更接近实际情况，考察由多个供应商、一个制造商(有多个产地)、多个仓库以及多个销售地构成的供应链网络。其中供应商提供不同的原材料，制造商生产不同种类的最终产品，仓库分别向不同的销售地提供最终产品。供应商有着充足的供应能力，同时制造商面对的销售市场的需求是不确定的。供应链的运作目标是要进行绩效与风险的综合优化，实现价值创造，优化的过程中选择EVA作为绩效指标，并且要考虑风险的影响。

供应链运作中影响EVA的一个关键因素就是资本成本的不确定。随企业资本类别不同，资本成本主要表现为债务资本成本和权益资本成本两大类。其中债务资本成本包括了长短期借款资本成本；权益资本成本包括普通股及优先股等资本成本，计算EVA时扣除的资本成本是单个资本成本的加权平均值。从长期来看，企业的债务资本成本与权益资本成本都是不确定的，都是处在波动之中的。另一方面，供应链运作中会面临由未来产品需求不确定带来的经营风险，面对风险时不同风险偏好的决策者会做出不同的经济决策，从而会不同程度的影响供应链的运作绩效。因此，供应链的运作过程中要以需求与资本成本不确定时最优的EVA值为追求目标，并根据决策者对经营风险规避偏好来确定供应链的最优运作策略。

与模型相关的符号及其含义如下：

集合与索引:t为阶段(t=1,...,T)；s为情景(s=1,...,S)；p∈P,R,F代表最终产品、原材料和所有的最终产品与原材料；l∈LE,LOP,LA代表采购地、产地和销售地；(p,l)∈PLE,PLOP,PLA代表采购，生产和销售的产品与地点固定组合；(l,j)∈TC代表各地点之间的运输连接；(p,(l,j))∈PC代表产品与运输连接的固定组合；(p,r)∈BOM表示最终产品对原材料的BOM系数。

辅助变量：EVAs为情景S下的经济增加值；DOLst为情景s下t阶段的企业经营风险；TCMst为情景s下t阶段的边际贡献；NSst为情景S下t阶段的销售净收入；VCOst为情景s下t阶段的变动成本；CAst为情景s下t阶段末的流动资产；OCFst为情景s下t阶段的经营性现金流；OMst为情景s下t阶段未结项目管理产生的现金流；FMst为情景s下t阶段财务投资管理产生的现金流。

3 供应链鲁棒优化模型

根据Mulvey提出的鲁棒优化的概念方法，在Hahn与Kuhn[7]研究的基础上，用情景不确定性来描述需求与资本成本的不确定性，并采用经营杠杆系数衡量经营风险的大小，建立需求与资本成本不确定条件下的鲁棒优化模型。另外，因为需求本身的不确定性会使得它与给定情境下的实际需求不符，不能保证控制约束总是能满足，所以模型建立时需要在目标函数里引入度量这种需求不可行性的误差变量。

基于EVA与经营风险的供应链鲁棒优化模型的目标函数为：

(1)

其中，目标函数的第一项是预期的EVA；第二项是经营风险与决策者风险偏好参数γ的乘积；第三项是可行性惩罚函数，用来惩罚控制约束的偏差，ω为权重系数。决策的目标是希望在任意情境下都可以找到“仍然接近于”最优的解(解鲁棒)，并且这个最优解都是可行的(模型鲁棒)。通过权重系数ω可以度量获得一个模型鲁棒解与获得一个解鲁棒解的相对重要性。

采用经营杠杆系数来衡量经营风险，经营杠杆系数反映的是销售量与息税前利润(EBIT)之间的杠杆关系， 最终可用总的边际贡献和固定成本来计算，即

DOLst=TCMst/(TCMst-fc) ∀s∈S;t=1...T

(2)

从式(2)可以看出经营杠杆系数的计算是非线性的，为了便于后续优化求解，将式(2)进行线性化，具体过程如下：

令TCMst=Xst，则DOLst就可以看成是Xst的函数，即：

DOLst=f(Xst)=Xst/(Xst-fc) ∀s∈S;t=1...T

(3)

(4)

其中，函数值fn(Xnst)对应于第n段区间上的DOLst值。在此基础上，目标函数式(1)可描述为：

(5)

为了确保线性化后的目标函数符合实际意义，需要增加以下约束条件：

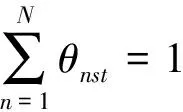
(6)

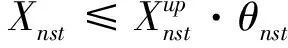
(7)

(8)

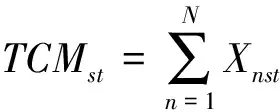
(9)

θnst∈{0,1} ∀n=1...N;t=1...T;s∈S

(10)

相对于原目标函数式(1)，经过线性化的目标函数式(5)增加了二元变量θnst，其含义为如果最优决策变量落在第n段区间内，即第n段区间被选中，则θnst=1，否则θnst=0；对应地，原目标函数中的决策变量TCMst以划分的每一段区间上的决策变量Xnst代替。约束(6)表明划分的所有N段区间中只有一个将被选中；约束(7)和(8)表明未被选中的区间所对应的决策变量只能为零。约束(10)衡量线性化后的决策变量Xnst与原决策变量TCMst之间的关系。上述约束(6)-(10)意味着如果优化后二元决策变量θn'st=1(n'∈{1,2,...,N}),即，第n'段区间被选中，说明最优TCMst值落在所选中的区间范围内，对应的最优TCMst=Xn'st。

EVA是税后净营业利润中扣除全部投入资本成本后的所得，其计算由税后净营业利润(NOPAT)、投入的资本和加权平均资本成本(WACC)三部分构成，NOPAT又是边际贡献扣减固定成本与所得税的结果，因此可以得到：

(11)

边际贡献等于销售收入减去变动成本，即

TCMst-(NSst-VCOst)=0 ∀s∈S;t=1...T

(12)

投入的资本构成了资产总额，等于固定资产与流动资产总和。流动资产仅考虑货币资金、存货和应收账款三项，由于应付账款属于无息负债，所以应将其从投入资本中减去，则流动资产的计算满足下式，即

(13)

加权平均资本成本的计算仅考虑债务资本中的长期借款和短期借款成本以及权益资本中的普通股成本，并假设企业的资本结构在一定时期内是固定不变的，则企业加权平均资本成本的计算满足下式，即

waccst=λ·DSRst·(1-z)+φ·ESRst+η·LSRst·(1-z) ∀s∈S;t=1...T

(14)

销售收入是指销售的净收入，等于销售收入总额减去销售成本总额，销售成本仅考虑产品的营销成本，即

(15)

变动成本总额由采购成本、生产成本、加班成本、储存成本和运输成本构成，同时还考虑了保理损失与现金折扣，即

(16)

建立基于价值创造的鲁棒优化模型要同时考虑与供应链资金流相关的财务约束以及与供应链物流相关的非财务约束。因此，模型还需要以下源自资金流的财务约束条件与源自物流的非财务约束条件。对于源自供应链资金流的财务约束，假设应收账款与应付账款中未结清的条款都有一个一年期的偿还期限，但是保理与扣除现金折扣后的提前付款可以用于资金的偿付管理。

销售收入减去保理总额即为应收账款的总额，应收账款约束为：

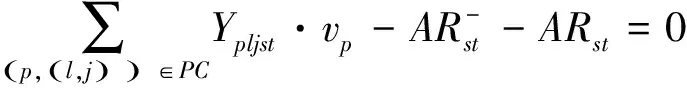
(17)

采购成本减去提前付款总额即为应付账款总额，应付账款约束为：

(18)

现金约束根据现金流量表，主要考虑经营现金流，未结项目管理产生的现金流以及投融资管理产生的现金流。现金约束为：

Cst-1-OCFst+OMst+FMst-Cst=ect∀s∈S;t=1...T

(19)

经营现金流：

(20)

未清项目管理产生的现金流：

(21)

财务管理产生的现金流：

FMst=FIst-1·(1+FIrst)-FIst-DSst·(1+DSRst-1)+LDSt-LDSt-1+LESt-LESt-1-LDSt·LSRst

∀s∈S;t=1...T

(22)

为保证流动性，必须保留一部分货币资金，最小现金约束为：

Cst≥Cmin∀s∈S;t=1...T

(23)

DSst≤DSmax∀s∈S;t=1...T

(24)

假设资本结构保持不变，则长期借款、短期借款以及普通股成本三种资本来源所占比重满足以下约束：

DSst-1+LDSt-1+LESt-1=fa+CAst-1∀s∈S;t=1...T

(25)

DSst-1=λ·(fa+CAst-1) ∀s∈S;t=1...T

(26)

(27)

(28)

初始值约束：

FIs0=FI0；ARs0=AR0；Cs0=C0；DSs0=DS0；APs0=AP0∀s∈S

(29)

非负约束：

(30)

源自供应链物流的约束条件要考虑到生产能力与储存能力有限的情况下采购、生产、运输及储存的数量，生产能力可利用分包商提供的加班得以扩展。

最终产品库存平衡约束：

(31)

原材料库存平衡约束：

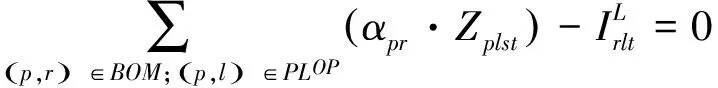
(32)

原材料与最终产品的期初与目标库存：

(33)

生产可用的原材料约束：

(34)

仓库可运往销售地的产品量约束：

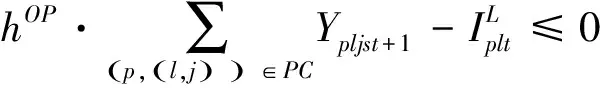
(35)

营运地生产能力约束：

(36)

营运地储存能力约束：

(37)

生产能力扩展约束：

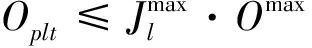
(38)

需求约束：

(39)

需求扩展约束：

nc·Mplst≤dplst·Mmax∀(p,l)∈PLA;∀s∈S;t=1...T

(40)

非负约束：

(41)

4 应用分析

考虑一个以洗衣皂、洗衣粉和洗洁精为主要产品的日用化工产品制造商，它有2家主要的原料供应商，有两个仓库和五个销售地，由此构成了一条备货型的供应链，包括采购，生产，运输和销售四个环节。供应商1只提供一种原材料，供应商2提供两种原材料，由于产地生产能力有限，产地1只生产两种产品，产地2生产三种产品。最终产品在运往销售地之前需存放在两个仓库中，原材料只存放在产地。供应链的运作目标是实现价值创造，结合建立的鲁棒优化模型对该供应链运作的具体情况进行仿真模拟。具体供应链的网络结构如图1所示：

根据企业的历史数据可知，两个产地的生产能力均为630000件，储存原材料的能力均为525000件，单位生产成本和储存成本分别为2元每件与0.1元每件；生产能力可通过加班扩大30%，单位加班成本为0.5元每小时；两个仓库的储存能力都为900000件，储存成本为1元每件；五个销售地的基本市场需求情况如表1所示：

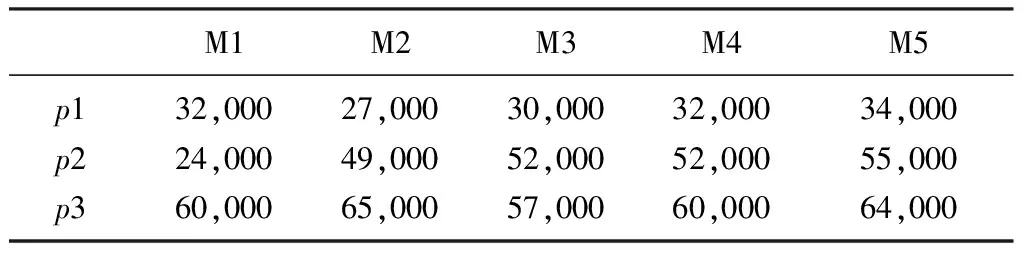
表1 市场基本需求情况表

图1 供应链布局，运输单位成本和产品分配图

运输的单位成本与产品的分配如图1所示。其他参数值如下：

产品p1与p2由1单位的r1和r2构成，产品p3由1单位的r1与r3组成，表2给出了产品与原材料的主要数据。最终产品与原材料的期初库存与目标库存如表3所示。

表2 最终产品与原材料的主要数据

表3 期初与目标存货水平

考虑13个规划期，每个规划期有5种不同的情形，每个情形的出现都有一定的概率，情景因素的潜在随机过程是由一个三角形分布确定的，这个三角形的最短边为0.7，最长边为1.2，中边为0.9。债务资本与股权资本在每个时期都是相同的，但是任一时期的五种情景下是不确定的，具体与情景有关的信息如表4所示：

表4 与情景有关的数据表

不同情景下的市场需求可根据式(41)，利用情景因素和振幅为35%的谐波震荡通过销售地的基本市场需求推知。

(42)

表5 确定与不确定情况下目标函数值

从表5的数据可以看出，在需求和资本成本均确定情况下的目标函数值大于不确定情况下的目标函数值，而且这种差异会随着不同的风险偏好而变化。进一步计算可以得到目标函数值的最小差异率为3.25%左右，最大差异率为6.67%左右，这说明即便在需求和资本成本均不确定时仍可以得到较为理想的结果，所得到的最优解具有鲁棒性。

为了进一步的分析，计算出在不确定情况下EVA与经营杠杆系数在不同风险偏好下的变化情况，具体结果分别如图2和图3所示。

图2 EVA随γ的变化趋势

图3 经营风险随γ的变化趋势

从图2和图3可以看出，随着风险偏好参数的增大，企业的EVA与经营杠杆系数整体上呈下降趋势，具体来说，在风险偏好γ=200时，EVA与经营杠杆系数呈现急剧的下降状态，在风险偏好达到一定范围之后，企业的EVA与经营杠杆系数的变化便没有那么敏感，几乎保持不变。并且图2与图3的变化趋势也表明，越是厌恶风险的决策者，越愿意牺牲较大的EVA来保持较低的经营风险。

由于模型中的存货与情景无关，决策者是在出现某一具体的情景前便做出存货的决策，根据建立的模型可计算分析不同风险偏好的决策者对于存货决策的选择，具体结果如图4所示。从图4可以看出，在13个规划期中，存货量随着季节性的波动而波动，并且在中期达到最大。除了第12个规划期外，风险偏好型的决策者一般会选择保留更多的存货以满足未来的需求，进而追求更大的企业EVA；而风险规避的决策者面对未来需求的不确定性却选择相对保守的存货策略，以降低存货量过多带来的风险。

图4 不同风险偏好参数下的存货

图5 δplst随ω的变化情况

此外，权重系数ω是用来权衡解鲁棒与模型鲁棒的，权重系数越大表示越倾向于模型鲁棒，系数越小越倾向于解鲁棒，计算出γ=200时不同权重系数下需求未满足δplst的变化情况如图5所示。图5中，横轴表示不同情境下的市场需求量，纵轴表示未能满足的需求量，可以看出随着ω值的增大，需求未满足量随着需求变化的幅度越小。当ω=0时其实就是线性规划方法，未满足需求量对需求的敏感性很强，在鲁棒优化模型中，这种敏感性则大大降低了，这说明我们所建立的鲁棒优化模型能更好的免受不确定性因素的影响。当ω增大到一定程度的时候(ω=2)，未满足需求量不存在，此时模型达到了完全的模型鲁棒，并且在此时仍能找到最优解，可见根据模型得到的最优解都是可行的。说明我们所建立的鲁棒优化模型能够实现模型鲁棒和解鲁棒，决策者可以通过选择不同的权重系数侧重于解鲁棒或模型鲁棒。

5 结语

要实现供应链价值创造的运作目标，必须将绩效与风险管理结合起来。EVA作为体现价值创造的重要财务绩效指标，资本成本是其核心的影响因素，现实中资本成本会随着贷款利率及股东要求的报酬率的波动而波动。需求不确定时，经营风险也是影响价值创造的重要因素。本文用鲁棒优化的方法，将EVA作为绩效指标，考虑决策者对经营风险的规避偏好，采用已知概率的离散情景来描述需求与资本成本的波动，得到了以价值创造为目标的供应链鲁棒优化模型。数值算例的结果表明，能够在需求和资本成本均不确定时找到所建模型具有鲁棒性的最优解，而且决策者越是厌恶风险其决策就越保守，会为了保持较低的经营风险而宁愿牺牲较大的EVA值。同时，我们所建立的鲁棒优化模型也能够实现模型鲁棒，决策者可以依据对解鲁棒与模型鲁棒的相对重要程度的判断选择不同的权重系数，保证供应链运作的鲁棒性，提供了对供应链绩效与风险进行综合优化从而实现价值创造的有效方法。

[1] Young S D, O’Byrne S F. EVA and value-based management: A practical guide to implementation[J].New York：McGraw-Hill Professional, 2001.

[2] Ritchie B, Brindley C. Supply chain risk management and performance[J].International Journal of Operations & Production Management, 2007,27(3):303-322.

[3] Ray R. Economic value added: Theory, evidence: A missing link [J].Review of Business, 2001, 22(1/2)：66-70.

[4] Christopher M, Ryals L. Supply chain strategy: Its impact on shareholder value[J].International Journal of Logistics Management, 1999,10(1):1-10.

[5] Walters D. The implications of shareholder value planning and management for logistics decision making[J]. International Journal of Physical Distribution & Logistics Management, 1999, 29(4):240-258.

[6] Lambert D M, Pohlen T L. Supply chain metrics[J]. International Journal of Logistics Management, 2001, 12(1):1-20.

[7] Hahn G. J, Kuhn H. Optimising a value-based performance indicatior in mid-term sales and operations planning[J]. Journal of the Operational Research Society, 2011, 62(3):515-525.

[8] Pongsakdi A, Rangsunvigit P, Siemanond K, et al. Financial risk management in the planning refinery operations[J].International Journal of Production Economics,2006, 103(1):64-86.

[9] You Fengqi, Wassick J M, Grossmann I E. Risk management for a global supply chain planning under uncertainty: Model and algorithms[J].AIChE Journal, 2009, 55(4):931-946.

[10] Goh M, Lim J Y S, Meng Fanwen. A stochastic model for risk management in global supply chain networks[J]. European Journal of Operational Research, 2007, 182(1):164-173.

[11] Sodhi M S, Tang C S. Modeling supply-chain planning under demand uncertainty using stochastic programming: A survey motivated by asset-liability management[J]. International Journal of Production Economics,2009, 121(2):728-738.

[12] Scholl A. Robust Planung und optimierung: Grundlagen, konzepte und methoden-Experimentelle Untersuchungen[M].Heidelberg-Verlay:Springer,2001.

[13] Mulvey J M, Zenios S A. Robust optimization of large-scale systems[J].Operations Research, 1995, 43(2): 264-281.

[14] Yu C S, Li H L. A robust optimization model for stochastic logistic problems[J]. International Journal of Production Economics,2000, 64(1-3):385-397.

[15] Leung S C H, Tsang S O S, Ng W L, et al. A robust optimization model for multi-site production planning in uncertainty environment[J]. European Journal of Operational Research, 2007, 181(1):224-238.

[16] Aghezzaf E. Capacity planning and warehouse location in supply chains with uncertain demands[J]. Journal of Operational Research Society, 2005, 56(4):453-462.

[17] 李春发,徐伟,朱丽. 考虑风险偏好的动态生产库存问题的鲁棒优化模型[J]. 运筹与管理, 2014, 23(5):48-54.

[18] Hahn G J, Kuhn H. Value-based performance and risk management in supply chains: A robust optimization approach[J].International Journal of Production Economics, 2012,139(1):135-144.

[19] Tang C S. Perspectives in supply chain risk management[J]. International Journal of Production Economics, 2006, 103(2):451-488.

[20] Christopher M, Towill D R. Developing market specific supply chain strategies[J]. International Journal of Physical Distribution and Logistics Management, 2002, 13(1):1-14.